Arnold变换在二值图像置乱应用中若干问题讨论



Arnold变换在二值图像置乱应用中若干问题讨论

廖日军，李雄军，徐健杰，李金龙，冼建标，何小雨

深圳大学物理科学与技术学院，深圳518060

摘要:针对二值图像的特点，讨论了二维Arnold变换在二值图像置乱中的置乱周期问题，提出一种快速Arnold变换策略，即少点置乱法，分析比较Arnold逆变换方法，针对一步恢复原图中直接求矩阵乘方会产生当矩阵元素过大超出运算精度限制时的结果错误问题，提出一种迭代取模伴随矩阵逆变换法．研究结果表明，经Arnold置乱的二值图像，其置乱周期有可能是Arnold变换周期的1/2;只对二值图像中占像素比例较小的像素进行置乱的变换策略，可提高置乱速度;对变换矩阵迭代取模后再求伴随矩阵，可得到正确的一步恢复矩阵．二值图像Arnold变换中，综合应用少点置乱法和一步恢复图像方法，可显著提高变换与反变换的速度．

关键词:计算机应用;置乱变换; Arnold变换;二值图像; Arnold逆变换;图像加密

Received: 2015-05-03; Accepted: 2015-06-09

Foundation: University Students' Innovation and Entrepreneurship Training Program Foundation of Shenzhen University(201510590079)

图像置乱通过变换把图像变得杂乱无章，从而达到隐藏或加密信息的目的，通过相应逆变换反置乱可恢复原始图像．置乱变换有多种，其中Arnold变换因为其算法简单、周期性和非线性佳，在图像加密、信息隐藏和数字水印中广泛应用．目前，对Arnold变换的周期性、恢复算法和向三维、四维等多维扩展的研究比较多见［1-8］，但对其在二值图像上的具体应用研究仍较少［9］．与灰度图像Arnold变换相比，二值图像Arnold变换在图像置乱周期、变换与逆变换操作方法、密钥选择策略等方面的显著特点，使其在图像加密解密、版权保护、数字水印等领域有着广泛的应用价值．

目前Arnold变换恢复算法基本分为3种:基于周期性的向前或向后迭代置乱法［3，6］、一步反变换法［1，9］和解多个方程组［2，4］的方法，但在实际应用中各种方法的效率和具体操作鲜见研究．

本研究结合新型微点二维码研究项目的具体实践，针对二值图像的特点，讨论Arnold变换的置乱周期问题、快速运算策略和恢复变换计算问题，最后给出了实验验证结果．

1　二值图像快速置乱策略与置乱周期

图像Arnold置乱变换常表示为

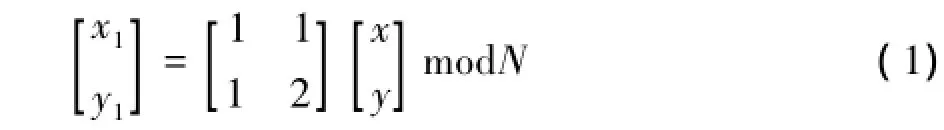
其中，x、y、x1和y1∈{ 0，1，…，N－1}，(x，y)和(x1，y1)是大小为N×N的数字图像一次Arnold置乱前及置乱后的像素坐标，记

则图像Arnold逆变换R使得

从而实现从(x1，y1)恢复出(x，y)．

若对原图进行k次Arnold置乱变换，依据模运算性质，有

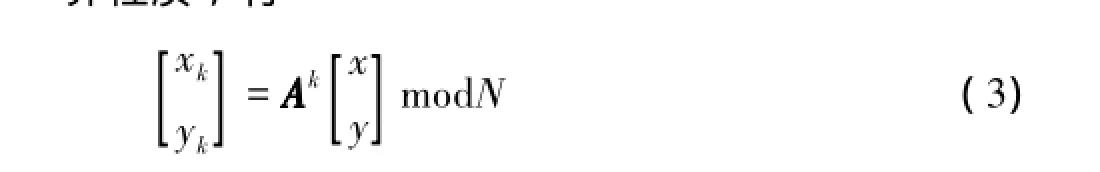
由于二值图像只有黑白两种像素，即0和1两种灰度值，因此只适于进行位置置乱，置乱前后黑像素或白像素数量不变，只是位置发生了变化．人们通常对图像中的每个像素依次进行置换，得到一次Arnold置乱的结果图像．置换后某黑像素可能被移到了原图像中某个白像素的位置，也可能是其他黑像素的位置，前一种情况能被视觉觉察到，但后一种情况则不可能察觉;白像素置乱亦如此．由此得到二值图像置乱变换的快速运算策略，即少点置乱法:统计图像中黑白像素的个数，若m = min(nB，nW)，其中nB和nW分别为大小为N×N的二值图像中黑白像素的个数．若置乱时只对占少数的像素进行运算，与全图像计算比较，在置乱变换上花的时间减少到原来的m/N2，在黑白像素数相差悬殊的情况即m＜＜N2/2时特别有效．注意:置乱图像时必须先以原图中占多数像素的颜色作为背景来初始化，对原图中少数个像素进行置乱计算后，再把置乱图像中对应位置的像素用前景颜色代替．以上策略既可用于二值图像置乱变换，也可用于反置乱逆变换．

Arnold变换是周期变换，周期的大小一般与图像大小即模值N有关，且与之呈非线性关系，见表1．对于给定自然数N，如式(1)的Arnold变换的周期mN是使式(4)成立的最小自然数n．

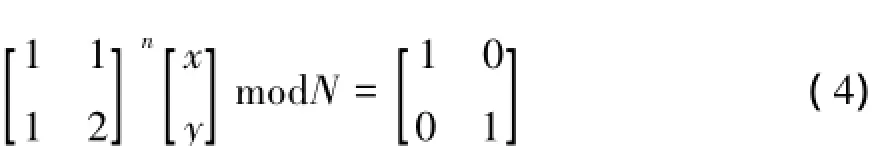
表1　不同阶数N下二维Arnold变换周期mNTable 1 mNfor Arnold transformation under different N

图像置乱周期是指原图像经过周期次置乱变换后，置乱图像恢复为原图．同样由于二值图像只有黑白两种像素，很有可能不到Arnold变换周期就已还原出原图．所以二值图像置乱周期ms不仅与Arnold变换周期有关，还与二值图像内容结构有关，即ms≤mN．根据Arnold变换图像置乱程度的半周期特性，ms最可能是Arnold变换周期mN的1/2，甚至1/4．

2 Arnold变换恢复算法

2.1 Arnold变换恢复算法对比分析

Arnold变换的快速高效恢复算法一直是人们追求的目标，特别当图像维数较大、置乱次数较多时，如何高效恢复图像尤为重要．根据Arnold变换的周期性和模运算的性质，人们归纳出迭代置乱法、一步反变换法和解方程组方法3种Arnold变换恢复算法．下面从效率和应用条件上对其进行对比分析．

问题描述假设某个大小为N×N的图像用Arnold变换置乱了k次，Arnold变换周期为mN，求解其恢复图像或恢复矩阵Tk．

迭代置乱法实质上是利用Arnold变换的周期性，有2种具体操作方式:①向前计算法，即向前继续一步步做mN－k次Arnold变换，可以得到原图像;②向后计算法，即采用式(2)的Arnold逆变换R做k次变换即还原原图．显然，向前法需已知周期mN，才知道要向前变换多少次;向后法则无需知道mN．虽然Arnold变换计算简单，但从图像还原效率考虑，向前法更适于k≥mN/2的情况，而向后法则当k较小时更有效．

但总的来说，迭代置乱法的计算效率分别与置乱次数k和图像大小正相关，图像越大，迭代置乱操作耗时越长．

孔涛等［2］通过分析式(1)中的像素位置范围，得到2种情况下的各2个方程组，求解联立方程组的解，两种情况解集的并就是所求的反变换．该方法仍需反复迭代k步，效率不高．

依据式(3)可得一步反变换为

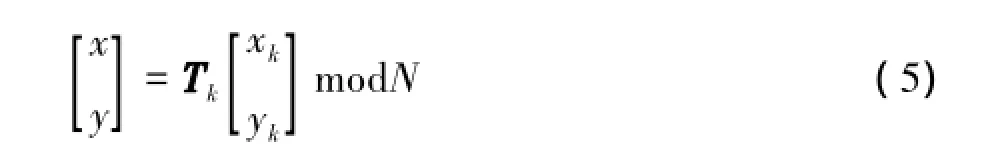
求解式(5)可得3种求逆变换Tk为

如果事先计算好对应各种置乱次数k的一步还原逆矩阵Tk1或Tk2或Tk3，可采用一步反变换高效恢复原图．在实时性要求高的场合，牺牲一点内存换取恢复速度是值得的．

以上3种求取恢复矩阵Tk的方法中都涉及矩阵乘方问题．采用Matlab进行计算时，对较大的置乱次数k，矩阵元素很快就大到超出计算精度的范围，从而得到错误结果．以N = 25为例，当k = 38时，矩阵Ak为

当k = 39时，Ak太大，超出了Matlab精度范围，致使求模结果出错

而正确的恢复矩阵是把式(9)中的矩阵元素20改为21．所谓差之毫厘，失之千里，之后的结果怎么都不正确了，变换周期为50也无法验证．因此，本研究提出一种迭代取模伴随矩阵新方法，以期解决直接计算变换矩阵乘方的一步反变换法存在的这些问题．

2.2迭代取模伴随矩阵法求一次性反变换

迭代取模伴随矩阵新方法的基本思路是:不直接用Matlab求矩阵的k次乘方，而是在迭代相乘的每一步都进行求模运算．迭代k步后求得一步变换矩阵C，C的伴随矩阵求模即为一步恢复矩阵．算法如图1．

图1　迭代取模求一次性Arnold变换矩阵的伪代码Fig.1 Algorithm pseudo-code for finding the one-step Arnold tronsform by iterative moduloing

由图1步骤，求得一次性Arnold变换矩阵为

文献［1］指出，逆变换矩阵可以用正变换的伴随矩阵来求得，而Arnold变换属于矩阵变换的一种，且对于Arnold变换，det(A ) = 1，则其中，adj(A )为A的伴随矩阵．所以，k步Arnold变换的一步逆变换矩阵为

几次求模乘后，恢复矩阵的det(Tk)已不再为1，但不断求模使得它并不影响最终结果．

从上可见，此迭代取模伴随矩阵求逆变换方法与图像内容无关，适用于任何图像，包括二值图像和灰度图像．

3　结果与分析

为考察本研究有关方法的实际使用效果，采用Matlab进行实验验证，测试电脑配置如下: Dell OptiPlex 9010 Mini Tower，处理器:英特尔，第3代酷睿i7-3770@ 3.40 GHz四核，Windows 7专业版32 位SP1(DirectX 11)，内存为4 Gbit．

3.1二值图像置乱周期

图2是一张白色背景中含10个黑像素的10×10二值图像经Arnold变换逐步置乱的结果．由表1可知，Arnold变换周期为30．然而，原图经15次置乱后就恢复到原图，可见图像置乱周期为15，是Arnold变换周期的一半．说明图像置乱周期与Arnold变换周期是两个不同概念．

图2　经Arnold变换的10×10二值图像(置乱次数k，图像置乱周期为15)Fig.2 10×10 binary images scrambled by Arnold transformation from scrambling time k=1 to k=15(with scrambling cycle of 15)

从图2也可观察到，Arnold变换图像置乱度的半周期现象和上半周期与下半周期的图像置乱效果具有一定对称性［10-11］．

3.2二值图像快速置乱变换效率实验

对多种不同大小、或黑底或白底、具有少数前景色像素的图像，在Matlab环境下进行Arnold变换实验，置乱次数为1个周期，测试传统全部像素参与置乱运算和只有少数前景像素参与运算2种方法的时间，结果见表2．

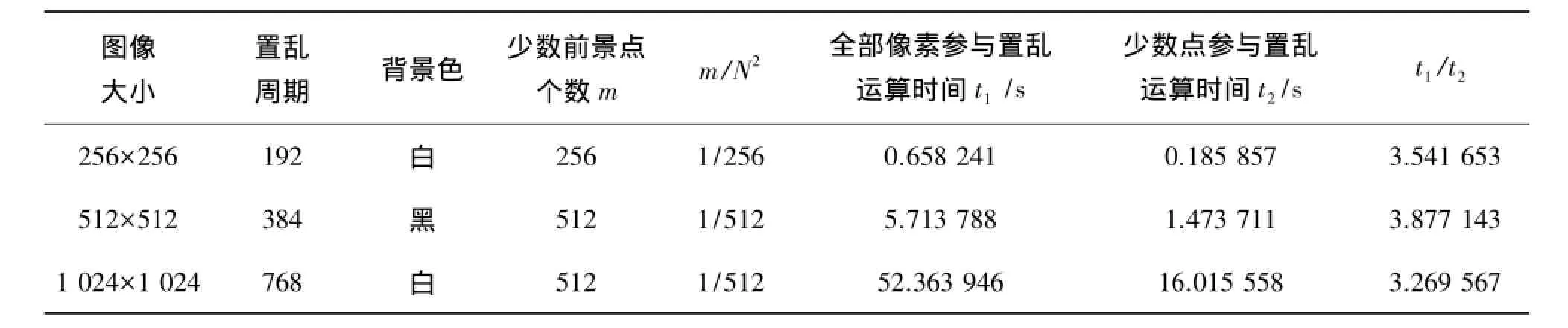
表2　二值图像Arnold置乱计算效率对比实验Table 2 Comparison of time costs for different scrambling strategies

由表2可见，对大小不同、黑白像素数量比例也不同的图像，以相应的置乱周期为置乱次数，只对少数点置乱的快速置乱策略可提高置乱速度，但并非与参与运算的像素个数成正比，究其原因是: Arnold矩阵变换的运算时间只占一次置乱变换整个运算时间的一小部分，取模运算需要时间，特别是循环条件判断、开辟缓存区等操作占去了大部分时间．同时，图像大小差异导致更显著的运算时间差异，运算时间更多地依赖于图像大小，进一步说明循环判断和开辟缓存数组上所花的时间占比较大．

3.3一步恢复矩阵的求解与效率实验

对大小为25×25的图像置乱k次，表3给出2种求取一步恢复矩阵方法的结果对照．

表3　直接求Ak取模法和迭代取模伴随矩阵法求得的Tk(N=25)Table 3 Comparison of Tkfor different methods(N=25)

由表3可见:

1)当k≤38时，2种方法求得同样的一步恢复矩阵，但从k = 39开始，直接求Ak取模法由于运算精度限制而得不到正确的恢复矩阵，致使直接求Ak取模法无法恢复原图．

2)本研究提出的迭代取模伴随矩阵法验证了阶数N为25时求取Arnold变换一步逆阵的正确性及其周期为50．

3)迭代取模伴随矩阵法所求恢复矩阵的行列式值大部分不再为1，但每步的求模运算保证了行列式值非1对最终结果无影响．

下面用256×256的白底图像含少数个黑色像素的图像进行实验，考察该改进方法在时间效率上的表现．

取k = 87和113，置乱周期为192．依据迭代取模伴随矩阵法，分别求得一步恢复矩阵为

首先，对图3的原图分别进行87次和113次置乱，在置乱图像上随意画上一笔来模拟污损，分别用T87和T113对有无污损的置乱图像进行相应一步反置乱．结果如图3，对无污损置乱图像，所求恢复矩阵可一步还原原图;对有污损置乱图像，一步恢复矩阵同样可以恢复原图主要信息，同时说明了Arnold置乱加密的鲁棒性．

图3　二值图像经87次和113次Arnold置乱与恢复实验Fig.3 Scrambled images with/without defects and their recovery images for N=256，k=87 and k=113

表4列出了全部像素和少数像素参与运算2种情况下常规迭代法与一步恢复算法所花时间．迭代方法还分为向前迭代和向后迭代．

由表4可见，采用迭代取模伴随矩阵法与少点置乱策略相结合恢复原图有明显效率优势．由于置乱次数都接近半周期次数96，所以向前、向后的迭代恢复耗时相差不多;就迭代取模伴随矩阵的一步恢复法来说，只在少数黑像素上进行恢复计算比逐个像素运算，效率大大提高，这也验证了少点置乱法的效果．

表4　二值图像Arnold置乱恢复效率对比实验结果(N=256，nB=256)Table 4 Recovery efficiency comparison for a 256×256 binary image with 256 black pixels

结论

1)二值图像置乱与反置乱变换都只需对原图中所占比例少的像素进行计算，可提高置乱速度．

2)二值图像Arnold置乱周期不同于Arnold变换周期，它不仅与图像大小有关，而且与图像结构内容有关．当置乱周期小于Arnold变换周期时，最可能为1/2周期值，甚至1/4周期值．

3) Arnold变换恢复算法最快的是一步反置乱法．对维数大的图像，预先计算好对应不同置乱次数的恢复矩阵，在实时性要求高的场合不失为一种明智的选择．该恢复矩阵的求取不能直接求矩阵的幂，应该迭代相乘取模，再求其伴随矩阵即得对应某置乱次数的恢复矩阵．

4) Arnold变换在二值图像中同样存在半周期性现象和前后半周期一定的对称性，限于篇幅，我们将另文发表．

引文:廖日军，李雄军，徐健杰，等．Arnold变换在二值图像置乱应用中若干问题讨论［J］．深圳大学学报理工版，2015，32(4) : 428-433．

参考文献/References:

［1］Li Xiongjun．A generalized matrix-based scrambling transformation and its properties［C］//Proceedings of the 9th International Conference for Young Computer Scientists．Huangshan(China) : China Computer Federation，2008: 1429-1434．

［2］Kong Tao，Zhang Dan．A new anti-Arnold transformation algorithm［J］．Journal of Software，2004，15(10) : 1558-1563．(in Chinese)孔涛，张亶．Arnold反变换的一种新算法［J］．软件学报，2004，15(10) : 1558-1563．

［3］Zou Jiancheng，Tie Xiaoyun．Arnold transformation of digital image with two dimensions and its periodicity［J］．Journal of North China University of Technology，2000，12(1) : 10-14．(in Chinese)邹建成，铁小匀．数字图像的二维Arnold变换及其周期性［J］．北方工业大学学报，2000，12(1) : 10-14．

［4］Mao Leibo．Research on Arnold transformation algorithm and anti-arnold transformation algorithm［J］．Journal of Chongqing Technology and Business University Natural Science Edition，2012，29(3) : 16-21．(in Chinese)毛雷波．Arnold变换及其逆变换［J］．重庆工商大学学报自然科学版，2012，29(3) : 16-21．

［5］Wu Faen，Zou Jiancheng．Some necessary conditions for the periodicity of Arnold transformation of digital image with two dimensions［J］．Journal of North China University of Technology，2001，125(6) : 66-69．(in Chinese)吴发恩，邹建成．数字图像二维Arnold变换周期的一组必要条件［J］．北方工业大学学报，2001，125(6) : 66-69．

［6］Arnold V J，Avez A．Ergodic problems of classical mechanics，mathematical physics monograph series ［M］．New York: W A Ben-jamin Inc，1968．

［7］Sun Xiaolong，Wang Zhengyong，He Xiaohai．Application of Arnold transformation in non-square image scrambling［J］．Journal of Terahertz Science and Electronic Information Technology，2014(2) : 248-251．(in Chinese)孙晓龙，王正勇，何小海．Arnold变换在非方阵图像置乱中的应用［J］．太赫兹科学与电子信息学报，2014(2) : 248-251．

［8］Liang Ting，Li Min，He Yujie，et al．Method of improved image scrambling based on Arnold transform ［J］．Computer Engineering and Applications，2013，49(11) : 204-207．(in Chinese)梁婷，李敏，何玉杰，等．基于Arnold变换的改进图像加密算法研究［J］．计算机工程与应用，2013，49(11) : 204-207．

［9］Xu Haibo．Arnold transform algorithm for binary images ［J］．Software Guide，2011，10(10) : 68-70．(in Chinese)徐海波．基于Arnold变换的二值图像算法［J］．软件导刊，2011，10(10) : 68-70．

［10］Wang Xinxin，Bu Ting．An evaluation alorithm of image scrambling degree based on the image area［J］．Journal of Anhui University Natural Science Edition，2011，35(4) : 48-52．(in Chinese)王新新，布挺．基于图像表面积的置乱程度评价算法［J］．安徽大学学报自然科学版，2011，35(4) : 48-52．

［11］Xu Jiangfeng，Yang You．Analysis of scrambling performance of encrypted image［J］．Computer Science，2006，33(3) : 110-113．(in Chinese)徐江峰，杨有．加密图像置乱性能分析［J］．计算机科学，2006，33(3) : 110-113．

【中文责编:英子;英文责编:雨辰】

【电子与信息科学/Electrics and Electronics Information】

Corresponding author: Associate professor Li Xiongjun．E-mail: lixj@ szu.edu.cn

Citation: Liao Rijun，Li Xiongjun，Xu Jianjie，et al．Discussions on applications of Arnold transformation in binary image scrambling［J］．Journal of Shenzhen University Science and Engineering，2015，32(4) : 428-433．(in Chinese)

Discussions on applications of Arnold transformation in binary image scrambling

Liao Rijun，Li Xiongjun，Xu Jianjie，Li Jinlong，Xian Jianbiao，and He Xiaoyu

College of Physics Science and Technology，Shenzhen University，Shenzhen 518060，P．R．China

Abstract:Considering the characteristics of binary images scrambled by Arnold transformation，we discuss the scrambling period for binary images and propose an efficient Arnold transformation strategy，namely scrambling on fewer pixels(SFP)．By analyzing and comparing different anti-Arnold transformation methods，we present a one-step image recovery method，the adjoint matrix recovery after iteratively moduloing(AMRAIM)，which aims to avoid the error caused by accuracy limitations when directly computing the transform matrix power．Experimental results show that the scrambling period for scrambled binary images may be one half of that of the Arnold transformation depending on the image contents．The calculation speed is improved by scrambling pixels with less proportion in constituting the binary image．By iteratively moduloing the transformation matrix，we obtain the one-step Arnold transformation and its adjoint matrix for anti-Arnold transformation，which recovers the original image in a single step．Combining SFP and ARMAIM in binary image scrambling by Arnold transformation，the computational efficiency is improved．

Key words:computer application; scrambling transform; Arnold transformation; binary image; anti-Arnold transformation; image encryption

作者简介:廖日军(1992—)，男(汉族)，广东省梅州市人，深圳大学本科生．E-mail: 2012180045@ email.szu.edu.cn

基金项目:深圳大学大学生创新创业训练计划项目(201510590079)

doi:10．3724/SP．J．1249．2015．04428

文献标志码:A

中图分类号:U 491.1