基于改进PSO算法的水轮机PID调速器的参数设计

汪醒鹏

（湖南省水利水电科学研究所 长沙市 410007）

范 哲

（益阳市柘溪水电站 益阳市 413500）

水轮发电机组承担着将水能转化为旋转机械能，再将旋转机械能转化为电能的任务。与风能、水能、热能相比，电能对存储运送介质有特殊要求，电能不能大量存储，因此电能的生产和消费必须同时进行。GB/T 15945-2008[1]中规定：电力系统正常频率范围为50±0.2 Hz，频率偏差过大不仅直接影响发电机组自身稳定运行，造成电网解列，而且导致以电动机为动力设备的生产制造厂家产生大量废品。因此，水轮机调节系统必须根据用户负荷的变化不断调节水轮发电机的输出功率，水轮机调节系统的优劣性决定电能品质。水轮发电机PID 调速器参数优化的方法有：下降梯度法[2]、神经网络[3]、遗传算法[4]、模拟退火算法[5]等，这些方法对提高PID 调速器的调节品质均有重要的理论价值，但是下降梯度法要求提取精确的函数，处理能力有限；神经网络易于陷入局部最优；GA 算法进化速度慢，易于早熟。PSO 算法[6]具有并行处理、寻优效率高的特点，与结构简单、鲁棒性强的PID 调速器相适应。

基本粒子群算法在处理水轮机PID 调速器时会出现局部最优或收敛缓慢等问题，因此本文提出了一种改进的自适应PSO 算法，该算法根据函数寻优策略改进惯性权重对搜索能力的影响，提高求解精度并加快收敛速率。在此基础上引入微分进化算子[7]选取部分随机粒子进行变异处理，从而提高了种群的多样性，扩大搜索解空间的区域，避免早熟和局部最优，并利用matlab 对该模型进行仿真优化，仿真结果验证了该方法的正确性和有效性，为水轮机调节系统提供一种可行的控制方案。

1 水轮机调节控制系统matlab模型

水轮机控制系统主要由PID 控制模块和水轮机被控模块组成，控制模块[8]系统结构在matlab 建立如图1 所示模型。其中，控制模块中的Kp、Ki、Kd 为simulink 系统中的待优化参数，分别表示比例常数、积分常数和微分常数。被控模块Subsystem 中封装了水轮机调速系统被控对象，包括机械液压子模块[9]（MHS）、水轮机及引水系统子模块[10]（WDS）和发电机及负荷子模块[11]（GS）。Subsystem 模块、MHS 模块、WDS 模块、GS 模块的matlab 建模分别如图2、图3、图4 和图5 所示。

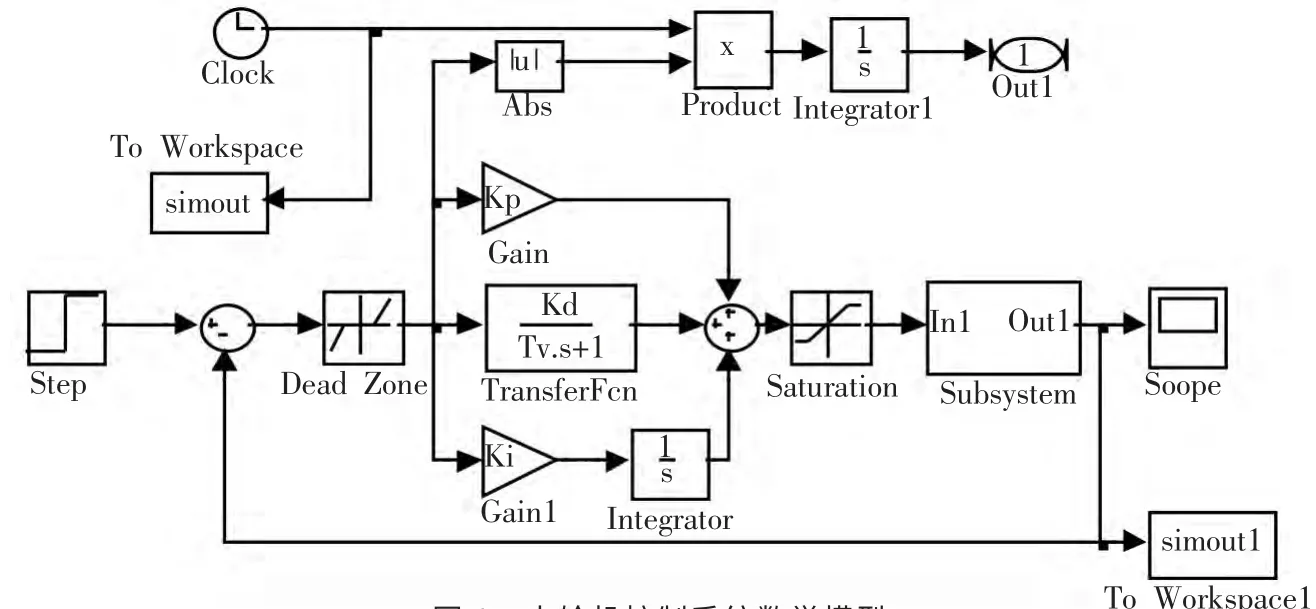
图1 水轮机控制系统数学模型

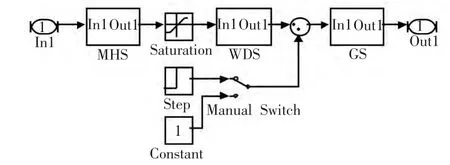
图2 水轮机调节系统被控模块

图3 机械液压模块MHS

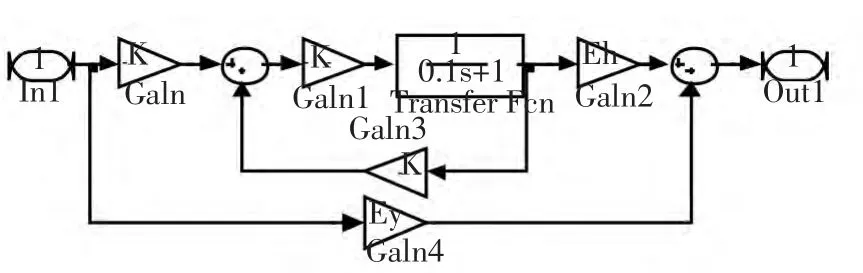
图4 水轮机及引水系统模块WDS

图5 发电机及负荷模块GS

2 改进的PSO优化算法

2.1 基本PSO 优化算法

与鱼群算法、Ant 算法相同，PSO 算法是从生物群体智能获得启示，利用并行计算的智能优化方法。Kennedy 和Eberhart 在研究鸟类捕食过程时，模拟其搜索解区域方式，将粒子抽象为潜在解，使每个粒子绑定一个适应度函数来决定其适应度值。粒子的速度决定粒子移动的方向和距离，速度随自身及其他粒子的移动经验进行动态调整，从而实现个体在可解空间中的寻优。粒子在求解空间中运动，通过追踪个体极值Pbest 和群体极值Gbest 更新个体位置。

基本粒子群算法思路： 存在一个n 维解区域搜索空间，随机分布m 个粒子(X1，X2,……,Xm),每个粒子均代表该空间中可能解，数学描述为n 维向量Xi=（Xi1，Xi2，……,Xin），根据计算每个Particle 的个体极值Pid=(Pi1,Pi2,……,Pin)与全体极值Pg=(Pg1,Pg2,……,Pgn), 利用速度调整公式实时跟新自身位置最终找出最优解。速度调整公式为：

式中c1和c2取[0,2]，r1和r2为程序自动随机数。

自身位置更新公式为：

基本粒子群算法参数依赖性小，计算效率高，但是在求解水轮机PID 调速器这类复杂模型过程中，易出现早熟和局部收敛，导致所得结果精度较低或者收敛速度过慢。

2.2 改进的PSO 优化策略

（1）自适应权重因子调整策略。

从基本粒子群算法速度调整公式可以看出，权重因子w 直接影响速度梯度，从而控制当前粒子在n 维空间中搜索解的能力。若w 数值偏小，粒子的记忆能力差，粒子移动缓慢，降低求解效率，若w 数值偏大，步长变大，利于搜索全体空间，但精度降低，不利于求得最优解，因此本文将采用一种自适应调整权重因子的方法，其表达式为：

式中 k，k+1 表示循环迭代次数，大量试验经验表明：Wmin取0.85，Wmax取2.2 时，收敛速度快，所求精度高。

通过限定权重因子的最小值并引入迭代次数增强其自适应能力后，在算法寻优前期，权重因子偏大，步长大，扩展搜索全域的能力，加快收敛速度。在寻优后期，权重因子偏小，利于在最优解附近微调整，从而利于调整精度。

（2）微分进化调整策略。

执行新的权重因子更新公式的同时，引入微分进化操作，在每一代的粒子中随机选取部分个体，进行变异进化，公式为：

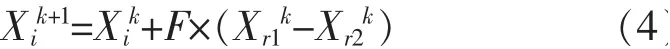
式中 k，k+1——粒子进化代数；

F——向量差分因子，其大小控制粒子的放大系数，本文取0.9。

2.3 改进PSO 算法的适应度函数

传统的PSO 算法优化水轮机PID 调速器参数中，引用时间绝对误差乘积指标ITAE 指标作为粒子的适应度函数，其表达式为：

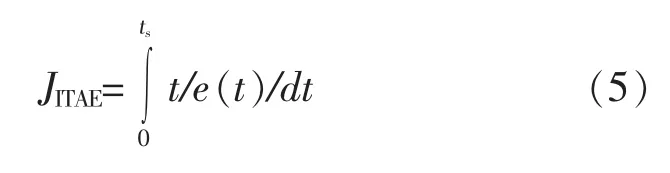
式中 t——时间；

ts——积分时间上限；

e（t）——误差。

为保证水轮机调速控制器具有满意的动态响应的特性，本文在ITAE 的基础上，综合考虑最大转速偏差相对值Xmax及控制量平方的积分，使用带加权系数的ITAE 作为粒子的适应度函数，其表达式为：

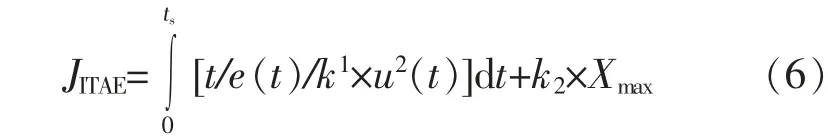
3 matlab中算法执行过程

在matlab 的simulink 模块建立本文图1～图5所示数学模型，在M 文件中编写改进PSO 算法程序，二者交互过程如图6 所示。

改进PSO 算法优化水轮机PID 调速器算法步骤如下：

①以随机方式赋值给每个Particle 原始位置和原始速度。②根据适应度函数计算出粒子适应度值。③将每个粒子的适应度值与其历史位置对比，优异者作为Pbest。④将粒子的适应度值与整个粒子群的最优历史位子作对比，优异者作为整个粒子群的Gbest。⑤根据式（1）和式（3）更新每个Particle 的移动方向和速度。根据式（2）更新粒子当前位置。⑥根据式（4）随机选取部分粒子进行变异操作。⑦根据式（6）输出性能指标，若满足条件跳出循环，否则转第②步。

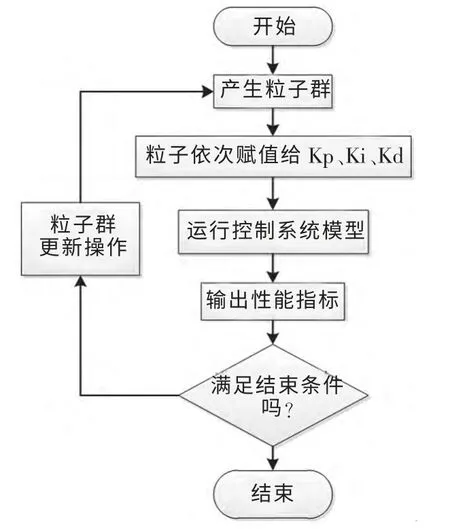
图6 算法流程图

4 工程实例分析

4.1 计算数据

已知湖南农村某小水电站1#混流式水轮机装机容量700 kW，额定水头97.9 m，最小水头96 m，最大水头99 m，额定流量0.71 m3/s，额定转速1 000 r/min，采用单机孤网带负荷模式运行。改进PSO 算法的试验参数设置范围如本文2.1，2.2，2.3 所述。

4.2 空载工况

将模型置于空载条件下，对试验仿真机加5%的频率扰动，研究机组转速过渡过程，其转速偏差结果如图7 所示: 蓝红线分别代表机组经过改进PSO算法优化前后的转速响应曲线，经过改进PSO 算法优化过的水轮机PID 调速器响应曲线超调量大幅度减小，调整时间也一半，整个过程有明显改进。机组输出性能指标结果如图8 所示：ITAE 进入稳定的时间加快，且稳定值下降幅度较大。

为验证改进权重惯性因子对PSO 算法的影响，将改进PSO 算法与基本PSO 算法的寻优收敛曲线进行对比，结果如图9 所示：在迭代次数小于20 时，红色收敛曲线的下降幅度大于蓝色线，说明在算法早期，改进PSO 算法收敛速度较快，当迭代次数大于20 时，红色收敛曲线线不断作微调整，说明改进PSO 算法精度作微调整。试验结果与权重惯性因子特性相吻合。

图7 转速偏差结果

图8 机组输出性能指标结果

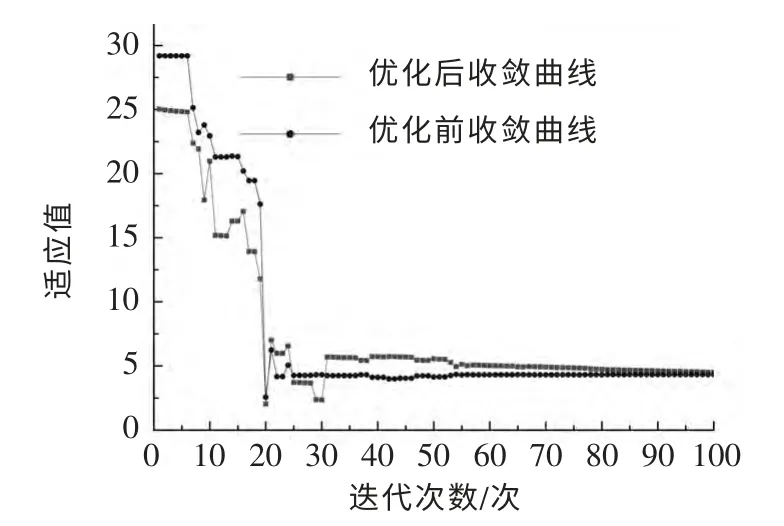
图9 寻优收敛曲线对比图

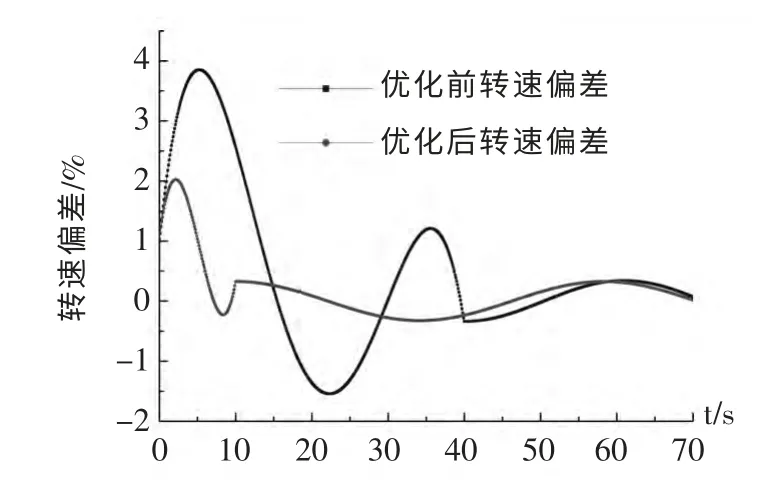
图10 10%试验负载下转速偏差结果

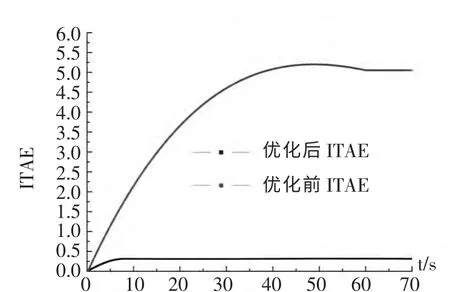
图11 输出特性指标

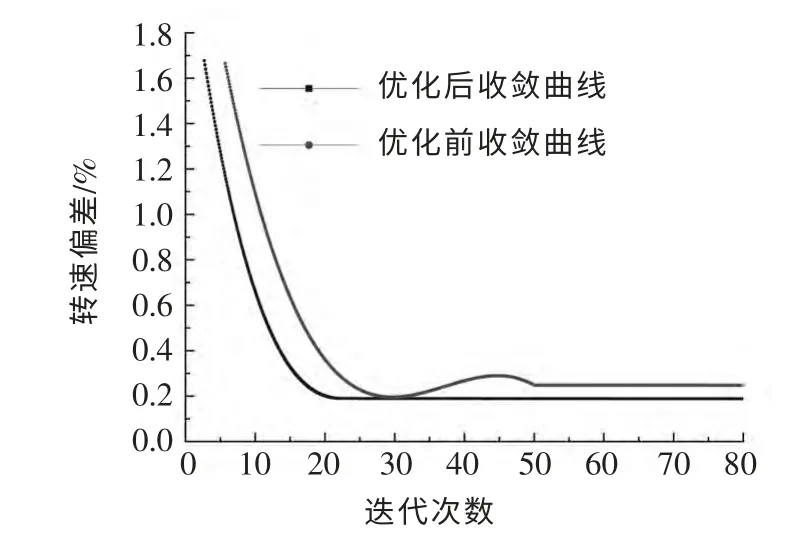
图12 寻优收敛曲线对比图

4.3 负荷工况

为研究水轮机调节的动态特性，将机组置于10%试验负荷下，其机组转速偏差结果和输出特性指标ITAE 分别如图10，图11 所示，结果表明：经过PSO 算法优化过的PID 水轮机调速器在孤网10%负荷扰动下，机组转速偏差的过渡过程比未经优化的机组过渡过程有明显改进；超调量减少、调节时间缩短、机组转速偏差的ITAE 指标下降。

同理，将改进PSO 算法与基本PSO 算法的寻优收敛曲线做比较，结果如图12 所示:在整个过程中，两种算法的调准精度相差较小，但改进PSO 算法的收敛速度较快。优化性能较好。

5 结 论

为了提高传统PSO 算法对PID 型水轮机调速器Ki,Kp,Kd 三个参数的优化质量，本文选择自适应调整权重惯性因子，该方法综合考虑了实际粒子群算法迭代过程中的收敛步长，平衡收敛速度和精确度的影响，避免陷入局部最优的同时提高了计算效率，同时引入微分进化因子，增加了全局搜索能力，确保了迭代过程中出现结果接近而早熟，最后通过5%频率扰动机组仿真试验和10%负荷扰动试验证明了改进PSO 算法优于基本PSO 算法，经过改进PSO 算法优化过的PID 调速器也具有较好的性能。

[1] 程远楚，张江滨.水轮机自动调节[M].北京：中国水利水电出版社，2010.

[2] 汤仪平，金福江. 最速下降法和共轭梯度的混合算法及全局收敛[J]. 华侨大学学报（自然科学版），2007，（2）:124-126.

[3] 侯树文，王琳琳，卢家涛，等. BP 网络模糊PID 控制在水轮机调速器中的应用[J]. 人民长江，2008，39（2）: 79-80.

[4] 孙美凤，张永华，张俊红. 水轮机调速器参数自整定遗传算法的研究[J]. 水力发电，2007，（5）.

[5] 王勇，刘厚林，袁寿其，等.离心泵非设计工况空化振动噪声的试验测试[J]. 农业工程学报，2012，28（2）：35-38.

[6] 鱼瑞文，周佩华，钱苗旺，等. 基于模糊复合最优粒子群算法的矿用电机控制系统参数优化[J]. 煤矿机械，2012，33（3）.

[7] 刘自发，张建华. 一种求解电力经济负荷分配问题的改进微分进化算法[J]. 中国电机工程学报，2008，（10）:100-105.

[8] 魏守平.水轮机调节系统仿真[M].武汉：华中科技大学出版社，2011.

[9] 魏守平.水轮机调节系统的MATLAB 仿真模型[J]. 水电自动化与大坝监测，2009，（4）.

[10] 曹程杰，莫岳平，刘丹丹. 基于改进遗传算法的水轮机PID 调速器最优参数整定[J].微计算机信息，2009，（34）.

[11] 罗旋，魏守平.基于MATLAB 的水轮机调节系统仿真[J].西北水电，2005，（3）.