闸坝水力学特性的三维数值模拟

闸坝水力学特性的三维数值模拟

钟海祥李彬徐爱兵

(中水电海外投资有限公司，北京100048)

【摘要】本文采用标准k-ε双方程紊流模型及基于水气两相流的VOF方法，运用FLOW3D软件对闸坝进行数值模拟，得出不同水位下的闸坝泄流能力，以及不同部位的闸室及消力池水面线、流速、压力等重要水力学要素。结果表明数值计算在一定程度上可以达到模型试验的效果。

【关键词】水气两相流；闸坝；数值模拟；泄流能力；水力学要素

中图分类号：TV135

Three-dimensional numerical simulation of gate dam hydraulic characteristics

ZHONG Haixiang, LI Bin, XU Aibing

(PowerChinaSinohydroResourcesLtd.,Beijing100048,China)

Abstract:In the paper, standard k-ε dual equation turbulence model, VOF method based on water-gas two phase flow, and FLOW3D software are adopted for numerical simulation on gate dam. Gate dam discharge abilities under different water levels, water surface line of gate chambers and stilling basin in different parts, flow velocity, pressure and other important hydraulic elements are obtained. The results shows that numerical calculation can reach the effect of model test to a certain extent.

Key words: water two-phase flow; gate dam; numerical simulation; discharge capacity; hydraulics elements

1概述

某闸坝设2孔泄洪闸，1孔泄洪冲沙闸，泄洪闸及泄洪冲沙闸过流面净空尺寸均为12.0m×21.0m(净宽×净高)，泄洪冲沙闸后布置深4.5m、长36m消力池。厂房段布置于枢纽中部靠左，为河床式厂房。闸坝坝顶高程494m，泄洪闸段闸室高程470m。

因库区有公路桥及铁路桥，闸坝泄流能力至关重要，而坝址上下游地形较为复杂，对泄流能力有一定程度的影响，规范公式无法精确算出。鉴于模型试验周期长、成本较大，故运用大型流体计算软件FLOW3D对其进行数值模拟计算，以求得闸坝泄流能力及水面线、流速、压力等重要水力学要素。

2数值模型的建立

2.1基本方程

本计算采用k-ε紊流数学模型，引入适用于分层两相流的VOF方法求解自由水面，Hirt和Nichols[1]提出的VOF法是目前处理带自由表面分层流问题的较理想方法。鉴于闸坝水流条件并不复杂，采用标准k-ε紊流模型计算，其连续方程、动量方程和k与ε方程分别为

连续方程

(1)

动量方程

(2)

k方程

(3)

ε方程

(4)

式(2)中，ρ和μ分别为体积分数平均密度和分子黏性系数。P为修正压力；μt为紊流黏性系数，可由紊动能k和紊动耗散率ε求出：

(5)

式(5)中，Cμ为经验常数，取Cμ=0.09。σk和σε分别是k和ε的紊流普朗特数，σk=1.0，σε=1.3。C1ε和C2ε为ε方程常数，C1ε=1.44，C2ε=1.92。G为由平均流速梯度引起的紊动能产生项，可以由下式定义：

(6)

引入VOF模型的k-ε紊流模型方程式(1)、式(2)、式(3)、式(4)与单相流的k-ε模型形式完全相同，只是密度ρ和μ的具体表达式不同，它们由体积分数加权平均值给出，即密度ρ和μ是体积分数的函数，而不是一个常数，可以由下式表示出来：

(7)

(8)

式(7)、式(8)中，αw为水的体积分数，ρw和ρa分别为水和气的密度，μw和μa分别为水和气的分子黏性系数。通过对水的体积分数αw的迭代求解，ρ和μ的值都可由式(7)、式(8)求出。

2.2计算条件

2.2.1闸坝模型

取坝轴线上游100m至坝下游160m的范围进行模拟计算，闸坝枢纽采用大型三维软件INVENTOR建模，生成STL文件后，导入Flow3D；河道模型通过AutoCAD生成的坐标点导入Flow3D。之后两者通过坐标转换对接，组合成整体模型，进行水力学的数值仿真计算。模型如图1、图2所示。

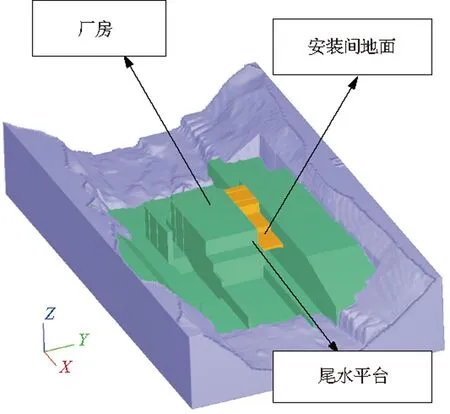
图1　闸坝三维模型(从下游看)

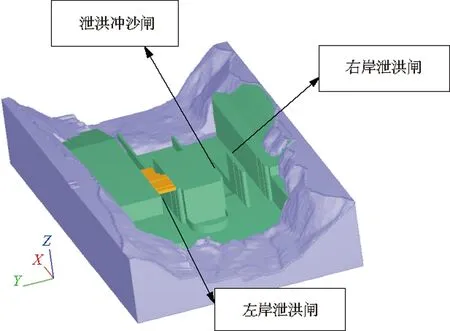
图2　闸坝三维模型(从上游看)

2.2.2计算区域

实体地形及闸坝在FLOW 3D软件中按障碍物考虑。坐标轴规定如下：

X轴——顺水流向，上游指向下游为正；

Y轴——垂直水流向，右岸指向左岸为正；

Z轴——竖直向，竖直向上为正，符合右手螺旋定则。

坐标原点为坝横0+000.00与坝轴线的交点处。

FLOW3D中网格的剖分范围即计算区域。计算区域包括固体部分和流体部分。固体部分的范围：上游地形段、上游铺盖段、闸室段、下游铺盖及消力池段、下游地形段。流体部分的范围：上游地形至下游地形的稳定水体。

网格剖分情况见图3和表1。因体型较为规则，故建立一个模块分析。

图3　闸坝及附近地形网格剖分

2.2.3边界条件

边界条件的设定见表2。

表1　计算区域剖分情况

表2　边界条件参数

边界条件说明：

Specified pressure为压力边界，用P表示。block1：X向最小边界条件为水流入口，F fraction设为1，X向最大边界条件为水流出口，F fraction设为1。

Symmetry为对称边界，用S表示。

2.2.4计算参数

各工况下进出口水位取值见表3。考虑河道长度及水流速度，设定流速计算时间为120s。河道糙率取0.04，闸坝糙率取0.014。

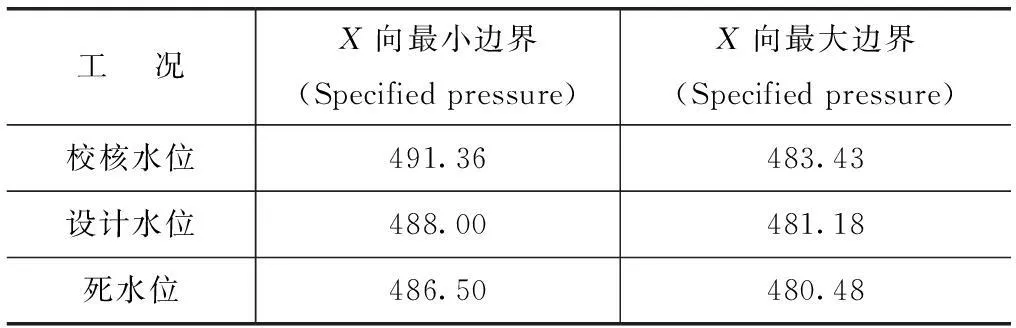
表3　各工况进出口边界条件

3计算结果与分析

3.1泄流能力

表4为各工况下闸坝泄洪能力，并与规范公式[2]对比分析，可知受地形及建筑物布置等因素的影响，模拟流量较规范公式计算流量偏小，但三工况下泄流量误差均在5%以内。

表4　各工况泄流能力

3.2校核水位下流态分析

图4为校核水位下枢纽区整体水流流态。0s时三孔工作闸门同时打开，120s后，进出口流量平衡，可视为水流已经稳定。整体来看，上游库区水流较为平稳，进入泄洪闸后，水面跌落，势能转化为动能，泄洪冲沙闸出现水跃；厂房后出现静水三角区；进入下游河道160m后，水流平顺，逐渐调整趋于稳定。

因泄洪冲沙闸泄洪时形成水跃，致使水面较其他位置高，为尾水平台周围水面最高处，此工况下，水流最高点为484.2m，距尾水平台0.8m，考虑到水跃波动较大，为安全计，应在此处设防浪墙等措施。

图4　整体流场

3.3校核水位下流速、压力分析

图5~图7为水流在X向的流速等值线图，图8为水流在Z向的典型断面(Z=476m)流速等值线图，可反映出整个平面的流速分布。

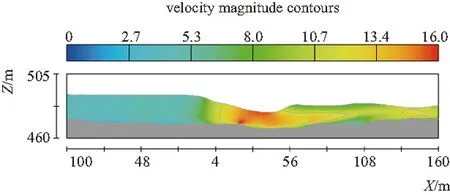
图5　流速等值线(Y=-8.5m)

图6　流速等值线(Y=-23.5m)

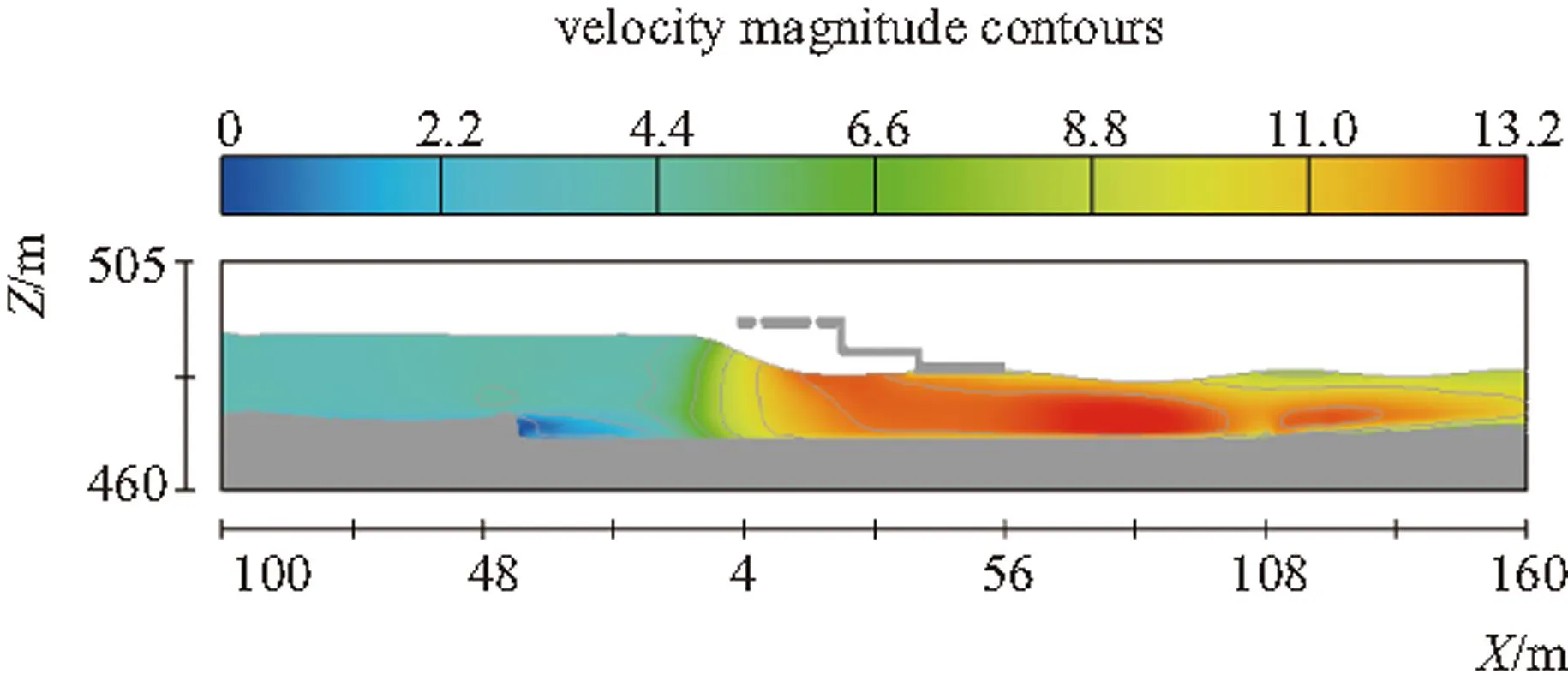
图7　流速等值线(Y=33.5m)

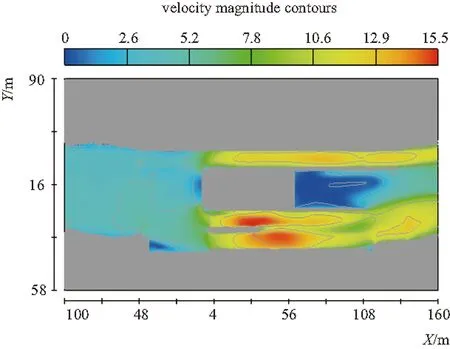
图8　流速等值线(Z=476m)

由图5~图8可知，右岸泄洪冲沙闸中轴线(Y=-8.5m)流速最大值为16m/s，发生在跌坎水面跌落处，消力池内形成明显水跃；右岸泄洪闸(Y=-23.5m)最大流速为15m/s，约在X=60m处，此处水面最低，后受泄洪冲沙闸的水流影响，形成水跃，但不明显；左岸泄洪闸(Y=33.5m)最大流速为13.2m/s，较右岸泄洪闸约小2m/s，分析认为是由于闸室水面已碰到尾水平台底板。

图9~图11为X方的压力等值线图，图12为Z方的压力等值线图，压力变化大致与水深相关，泄洪冲沙闸水面跌落处并未出现负压，左岸泄洪闸尾水平台底板出现有压流。

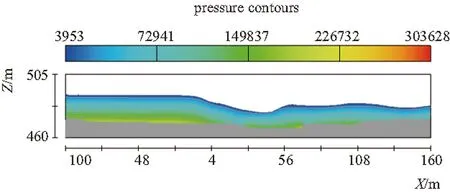
图9　压力等值线(X=-8.5m)

图10　压力等值线(X=-23.5m)

图11　压力等值线(X=33.5m)

图12　压力等值线(Z=476m)

4结语

本文利用k-ε紊流数学模型，引入适用于分层两相流的VOF方法求解，采用FLOW3D软件对闸坝泄洪能力及各水力参数进行了分析，结论如下：

a.受地形及建筑物布置影响，各水位下泄流能力均较规范公式偏小，但在5%以内，可对工程作一参考。

b.闸室整体水流流态较为平顺，但校核水位下泄洪冲沙闸至尾水平台处水面较高，应做一定防护措施。

c.一定程度上反映了流速、压力等水力学要素的分布情况。

鉴于数值计算的易操作、低成本和无比尺效应等优越性，在消能工的选型和优化设计工作中，数值模拟方法将发挥更大的作用，甚至可以代替相当一部分的试验，缩短试验周期。

参考文献

[1]Hirt C W，Nichols B D. Volume of Fluid (VOF) method for the dynamics of free boundaries[J].Compul.Phys.1981，39：201-225.

[2]DL/T 5166—2002溢洪道设计规范[S] . 北京：中国电力出版社，2002.