基于八叉树空间分割的NURBS曲面重构方法
王育坚,谭绍维,荆文鹏,董伟伟
(北京联合大学 信息学院,北京100101)
0 引 言
三维曲面重构在逆向工程、图像处理、计算机辅助设计和计算机视觉等领域得到应用[1,2]。三维模型数据结构复杂、数据规模庞大,使得点云的存储和压缩成为影响曲面重构算法效率的关键因素[3]。由于通过不同方法获取的点云数据量庞大、拓扑结构丢失,针对大规模点云的曲面重构方法仍然需要深入研究。本文提出一种基于八叉树空间分割的NURBS曲面重构方法,利用八叉树的快速收敛能力对点云进行分割、精简处理,采用NURBS曲面重构方法对局部网格曲面进行重构,使用八叉树和四叉树相混合的数据结构,渐进地进行曲面的重构。
1 八叉树空间分割方法
1.1 八叉树结构
在数据模型研究方面,研究者提出多种数据组织方法[4],提高了重构模型的精确度和运算效率。文献 [5]提出一种无指针八叉树的二元结构,并设计了八叉树的快速创建算法,适用于不同结构的八叉树。该方法既减少了模型的存储空间,又提高重构速度。文献 [1]采用空间分布式方法,将海量点云分配到多个服务器,采用并行访问技术,提高了数据管理的效率。从空间数据结构的特点看,八叉树的递归构建原理和空间划分规则非常适合散乱点云数据的处理。
八叉树是将四叉树推广到三维空间而得到的一种递归结构,可应用于三维空间实体的分割表示。从逻辑结构上看,八叉树采用树的结构,按X、Y、Z 这3 个不同方向,将三维空间实体分割为8 个大小相等的子立方体。然后,根据每个子立方体所含的目标来决定是否继续对子立方体进行八划分。重复下去,一直划分到每个子立方体或被一个目标充满,或没有目标,或其大小已成为预先定义的规模为止。显然,八叉树每个结点有8个或0 个子结点,其度为8或0。
八叉树物理结构分为规则八叉树和线性八叉树。规则八叉树要存储8个子结点的指针和一个父结点的指针,非叶子结点还需要存储下一个子结点的指针[6],存贮效率较低。
线性八叉树是一种算法效率较高的物理结构,采用8进制的前缀编码方法[5]。对于同一父结点的8 个子结点,具有最小x、y、z值的结点编号为0,相邻兄弟结点的编号沿x方向增加1,沿y方向增加2,沿z方向增加4,并在8个子结点编码中加入父结点编码,作为其前缀。为了计算方便,可以在编码后增加一串不同于0~7 八进制数的字符,保证八叉树结点编码q的长度一致,均为树的最大的深度。这样,八叉树结点的编码q代表分割空间后的立方体网格单元。
1.2 基于八叉树的点云分割模型
一般的散乱点云数据不适合直接进行曲面重构,需要对点云数据进行分割。点云数据的分割可以采用八叉树空间结构划分的思想。首先,构建一个包含所有点云在内的长方体包围盒,作为八叉树的根结点进行初始化。然后,进行八叉树递归分解。每一次分解后,点云数据散落在8个子立方体中。这样,通过采用八叉树体素分解方法,对包围盒进行递归分割,将点云模型逐级分解,直到达到规定的细分程度为止。
八叉树点云分割模型如图1所示,每个子结点表示对应的子立方体,圆圈表示该子立方体未被点云数据填满,需要继续分解;灰度小矩形表示该子立方体点云数据被填满,空白矩形表示该子立方体中没有点云数据,这两种情况都不需要继续分解。八叉树的叶结点中存储点集,每个叶结点中存储了散落在该立方体内的点云或抽样点数据。
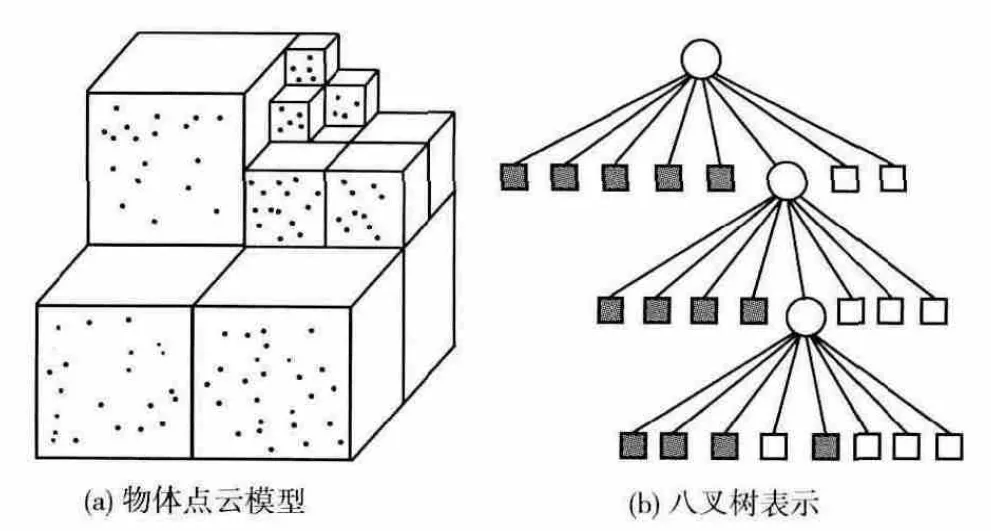
图1 八叉树结构
利用点云构建八叉树模型,子立方体细分的程度是一个首先需要解决的问题。立方体划分越细,落在每个子立方体内的点越少,数据丢失率低。但如果立方体划分太细,存在大量的冗余子立方体。反之,如果立方体划分太粗,模型精度不高。因此,立方体的划分规则必须高效、合理。
有两种常用的立方体划分方法,一种是根据点云密度设定细分的阀值[7]。八叉树深度决定子空间 (叶结点)个数以及每个子空间包含的平均点数。设实体空间点云总数为n,子空间平均点数为k,则叶结点数为n/k,八叉树深度h为
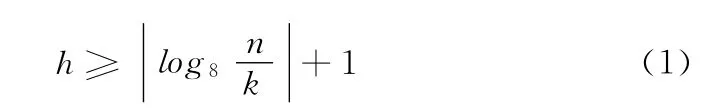
式中: “||”表示取整数运算。显然,当八叉树是满八叉树时,树的深度h最小。k是每个子立方体中点数的平均值,从总体上反映了立方体内点的密集程度。实际应用时根据点云总数n和八叉树深度h设定k值。将k作为分解结束的条件阀值,细分时检查每个子立方体,如果子立方体内的点数不大于k,则该子立方体停止分解;否则,需要对该子立方体继续进行分解,直到所有子立方体内的点云数满足阀值。
另一种立方体划分方法是根据子立方体的边长进行八叉树分割[8]。根据指定的点距,利用八叉树编码对点云进行空间邻域划分,把点云的空间包围盒分解为8个指定边长的子立方体;分解后在每个子立方体中都存在点云数据,在子立方体中迭代计算抽样点,精简数据量。这样压缩后,点云密度适中,并可以有效地得到每个点的局部几何信息。
对于一些形状复杂曲面的分割,上述方法都不好控制八叉树的深度。如果点云中的数据点都落在少数包围盒内,则划分得到的八叉树不平衡度高,不利于搜索计算。本文采用一种基于曲率的形状函数控制子体数,具体原理见2.2节。
2 NURBS曲面重构
2.1 NURBS曲面表示
围绕曲面重构,近年来提出了多种基于Delaunay、参数曲面或隐式曲面的曲面重构方法[9],这些方法具有几何量计算简单、显示不变形、便于控制等特点。但是,这些曲面重构方法大多涉及网格拼接和法向一致化计算问题,增加了算法的时间复杂度。对于复杂结构的模型,重构效果不理想。NURBS曲面拟合具有空间几何不变性、局部支撑性、光滑连续性等特点,是构建三维空间实体曲面的有效方法[10]。
NURBS非均匀有理B样条函数是在B样条函数基础上发展起来的,已被广泛应用于计算机辅助设计、制造和工程中。近年来,在三维建模领域也成为研究热点。
k×l次NURBS曲面有理分式表示为
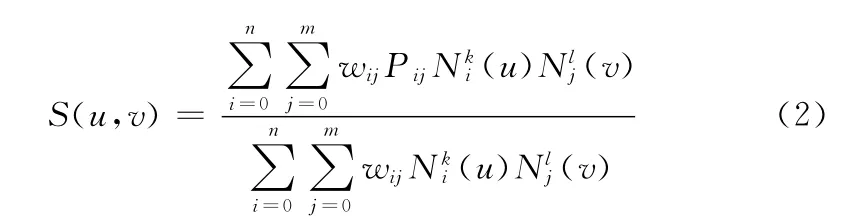
式中:Pij(0≤i<n,0≤j<m)是控制顶点,所有控制顶点构成一个控制网络;wij(0≤i<n,0≤j<m)为控制点Pij的权因子;Nki(u)(0≤i≤n)和Nlj(v)(0≤j≤m)分别是u、v方向的k 次、l次B样条基函数,它们分别由u、v方向的非均匀结点矢量U、V 按德布尔递归公式决定
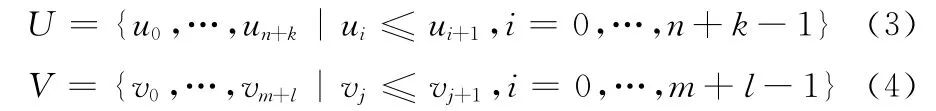
有关NURBS曲面重构的主要研究内容包括数据压缩、数据点参数化、单片曲面重构和曲面合并等,目标旨在提高参数化、建模的精度和效率[7]。NURBS能用统一的数学表示描述曲面,且能够通过权因子调整曲面形状,使得曲面形状易于控制。NURBS曲面拟合具有空间几何不变性、光滑连续性等特点。但NURBS方法也有缺点,当采用逐片构造方法拟合复杂拓扑结构时,需要对曲面片进行裁剪。并要考虑片与片之间的光滑拼接,难以保持接缝处光滑。
2.2 混合数据结构设计
模型在逻辑结构上采用一种八叉树与四叉树相混合的数据结构,如图2所示。混合数据结构由数据层和曲面层组成,数据层采用八叉树结构,曲面层采用四叉树结构。数据层利用八叉树对点云数据进行分割,最终在叶结点中生成控制点,并与曲面层进行链接。曲面层根据数据层八叉树叶结点提供的控制点数据,利用NURBS进行局部曲面拟合,然后采用四叉树结构对曲面进行合并。
利用八叉树结构分解点云时,在叶结点中除了存储子体的X、Y、Z空间信息,还存储了与点云数据相关的几何信息,如结点的边界、数据点的法向量坐标、所属曲面的编码等。采用广度优先方法建立八叉树,并确保八叉树相邻的4个叶结点属于一个局部曲面。
在存储结构上,曲面层四叉树并没有存储叶结点,而是共享了数据层八叉树的叶结点。这样数据层和曲面层构成一种扩展的八叉树-四叉树结构。
对形状复杂的曲面进行分割,1.2 节介绍的两种立方体划分方法存在一些缺陷,不容易控制八叉树的深度和平衡度。有些算法进行了些改进,在进行子结点分解时综合考虑点云密度阀值和子立方体的边长[11]。本文算法采用一种基于曲率的形状函数控制点数的方法。
对曲面进行参数化的一个基本原则是保证曲面在每个区间内都有数据点,即保证参数化的均匀,避免奇异情况的发生。抽样的疏密度取决于曲面的曲率,曲率越大,抽样点越密;反之,曲率越小,抽样点越稀。
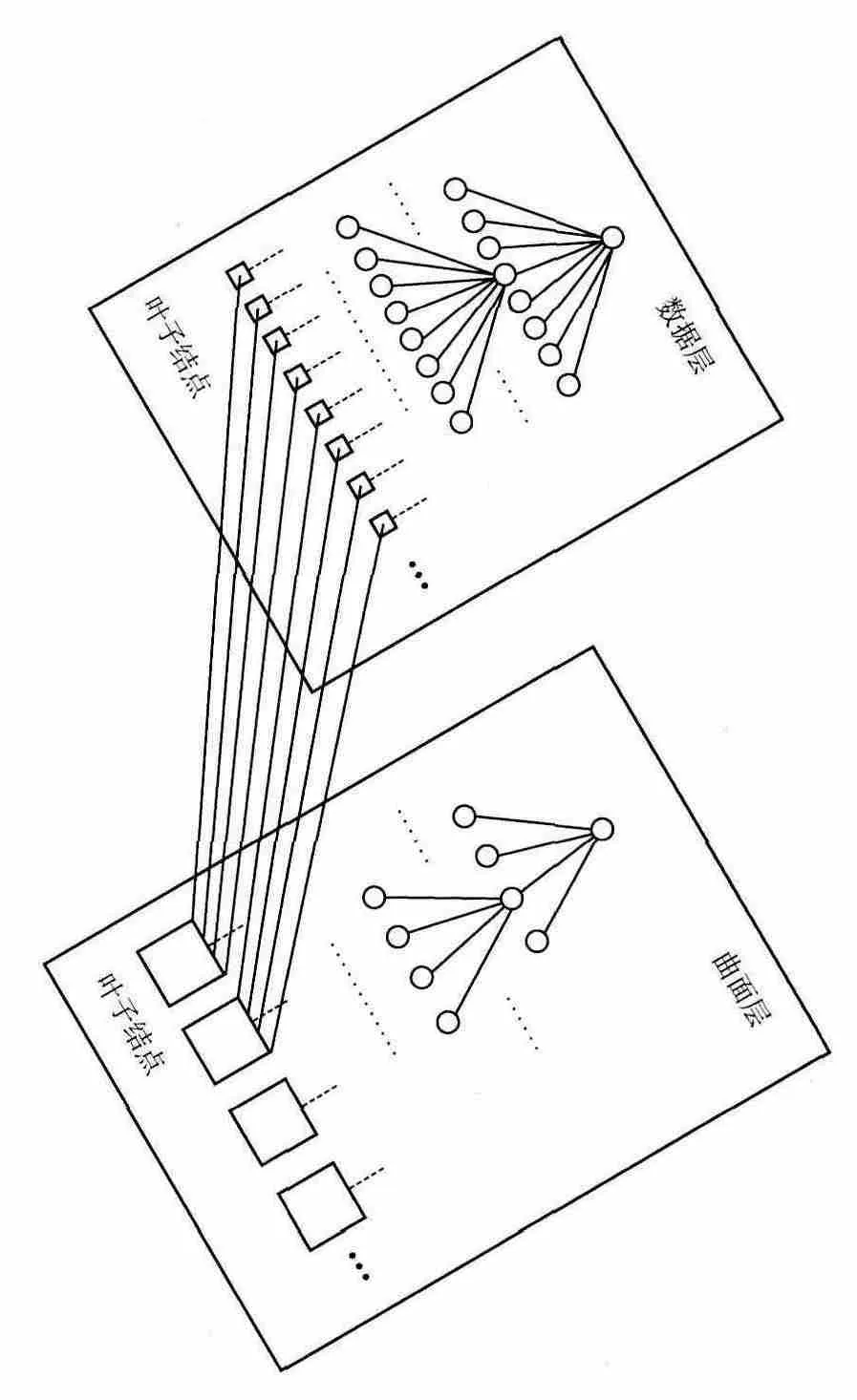
图2 八叉树-四叉树混合结构
设Q为一个曲面的采样点集,q(x,y,z)为点集Q 中任意一个点,f(x,y)为插值于Q 的曲面。令r(x,y)为体现曲面f(x,y)曲率的形状函数。显然,在形状函数r(x,y)较大的地方,所需的抽样点较多。因此,可以将形状函数r(x,y)作为是否继续进行子立方体分解的条件。根据网格不变性,形状函数r(x,y)只依赖于曲面固有的曲率测度[12],为
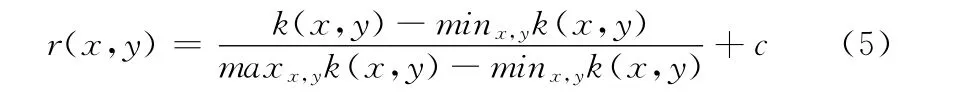
其中,c>0,为常数;k(x,y)是主曲率的几何平均值
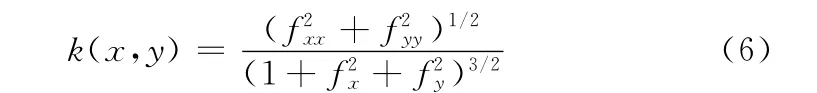
混合数据结构的C语言描述如下:


对传统的八叉树生成算法进行改进,在进行结点分解时将形状函数r(x,y)作为分支限界函数,以精简八叉树的结点数,保证八叉树的平衡度,这样提高算法的时间和空间效率。
八叉树生成算法的基本步骤如下:
(1)计算空间点云总数n,设置叶结点中的平均点数k,根据式 (1)估算八叉树深度h。
(2)计算包含所有点集的最小包围盒,作为八叉树根结点范围。按广度优先方式建立八叉树,存储结点相应的信息。
(3)计算子立方体内点云的形状函数r(x,y),如果满足分支限界函数值,则停止分解;如果不满足条件,则将子立方体分解为8个子结点。
(4)在八叉树分解过程中,停止分解的结点作为叶结点,存储所属局部曲面的编码。
(5)重复 (3)和 (4),直至停止所有子立方体的细分;为了控制八叉树的深度,当深度超过估算深度h (最小值)的2倍时也停止分解。
数据层八叉树叶结点的曲面编码属性表示该结点所关联的曲面。曲面层四叉树不存储叶结点数据,所有与曲面相关的数据层叶结点的几何数据也属于曲面层。曲面层四叉树最后一层的结点链接到数据层八叉树的叶结点。即曲面四叉树最后一层的结点需要存储数据层内对应的4个叶结点的指针,建立曲面与数据点的联系,以便进行曲面重构。
2.3 NURBS曲面重构方法
对于一个形状复杂的实体模型,利用NURBS 进行整体曲面的拟合很困难,因为点云数据本身结构散乱,不能直接根据数据形成矩形阵列[3]。可以按照实体形状的特征将点云划分为不同的区域,按区域将不同的数据点拟合成局部的曲面。前述已利用八叉树数据结构分割点云,把点集划分为足够小、互不相交的子集,这样就可以利用八叉树叶结点中的点云拟合一个矩形区域的曲面。
基于八叉树的每4个叶结点构成一个NURBS曲面的矩形区域,根据特征量建立数据点之间的拓扑关系[13],然后逼近生成其余的控制点。这样,将点数据划分成一系列的网格,然后在网格上进行四边形矩形区域的曲面重构。
根据点云建立曲面,需要对点云进行空间邻域划分[8]。设数据点q(x,y,z)所在子立方体的空间索引值为 (a,b,c),q=qn-1…qi…q1q0为与子立方体对应的结点的八进制编码。从q0、q1到qn-1表示叶结点到根结点的路径。
已知子立方体对应的八叉树结点编码q,可以求出数据点所在子立方体的空间索引值 (a,b,c)
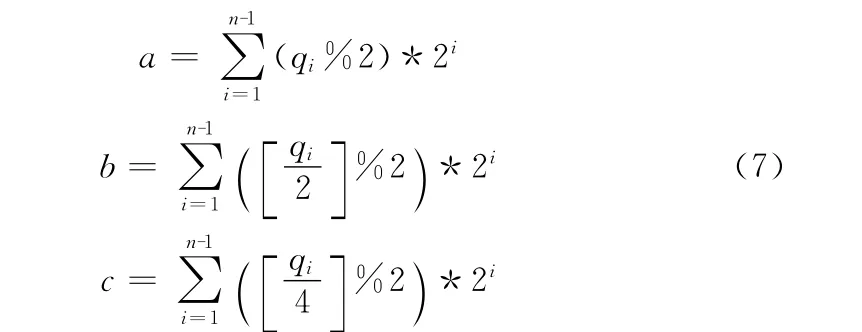
根据式 (7)可以求出八叉树叶结点的空间邻域坐标。叶结点作为曲面重构的4个控制点,其它控制点利用样条基函数进行插值得到。
曲面的次数取k=l=3,结点的重复度为4,u和v方向结点矢量两端的0 和1 的个数为4,根据式 (3)和式(4),可设曲面u方向的结点矢量为U(0,0,0,0,u4,u5,…,u3+n,1,1,1,1),v方向的结点矢量为V(0,0,0,0,v4,v5,…,v3+m,1,1,1,1)。考虑数据点分布不均匀,中间内结点的选取采用累积弦长法。
如果点云八叉树分割精度较细,局部矩形区域曲面的形状不复杂,为了简化曲面拟合,可以采用三次均匀B 样条逼近矩形区域曲面[14]。设Q 为矩形区域曲面的采样点集,qk(xk,yk,zk)为Q 中任意一点,且a≤xk<≤a+1,b≤yk≤b+1,pij是一个网格控制点,则受qk影响的4×4个控制点应满足

其中,Bi和Bj为样条基函数。
为控制点坐标添加约束条件
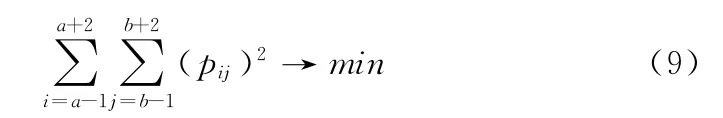
则可求得控制点坐标
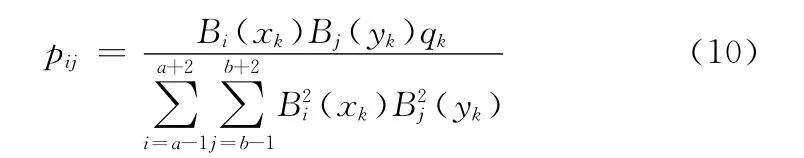
曲面采用四叉树结构表示,如图3 所示。利用链式结构存储曲面之间的关系,以避免曲面的拼接,方便曲面的合并。编码采用前缀编码[7],构造Hash表。混合模型通过数据层八叉树结点的曲面编码属性建立曲面索引,提高了搜索效率。
生成NURBS曲面后,4个曲面构成一个四叉树的叶结点,通过指针形成一个曲面递归结构。对应于控制网格的每4个小四边形网格都有一个共同点,即4个网格的交互点。对应于每个共同的交互点,建立与四叉树结点的链接,产生一个新的网格。每归并一次,旧的网格都可以被新的网格表示,这样不断的递归细分下去,最终使网格拟合到一张复合曲面。
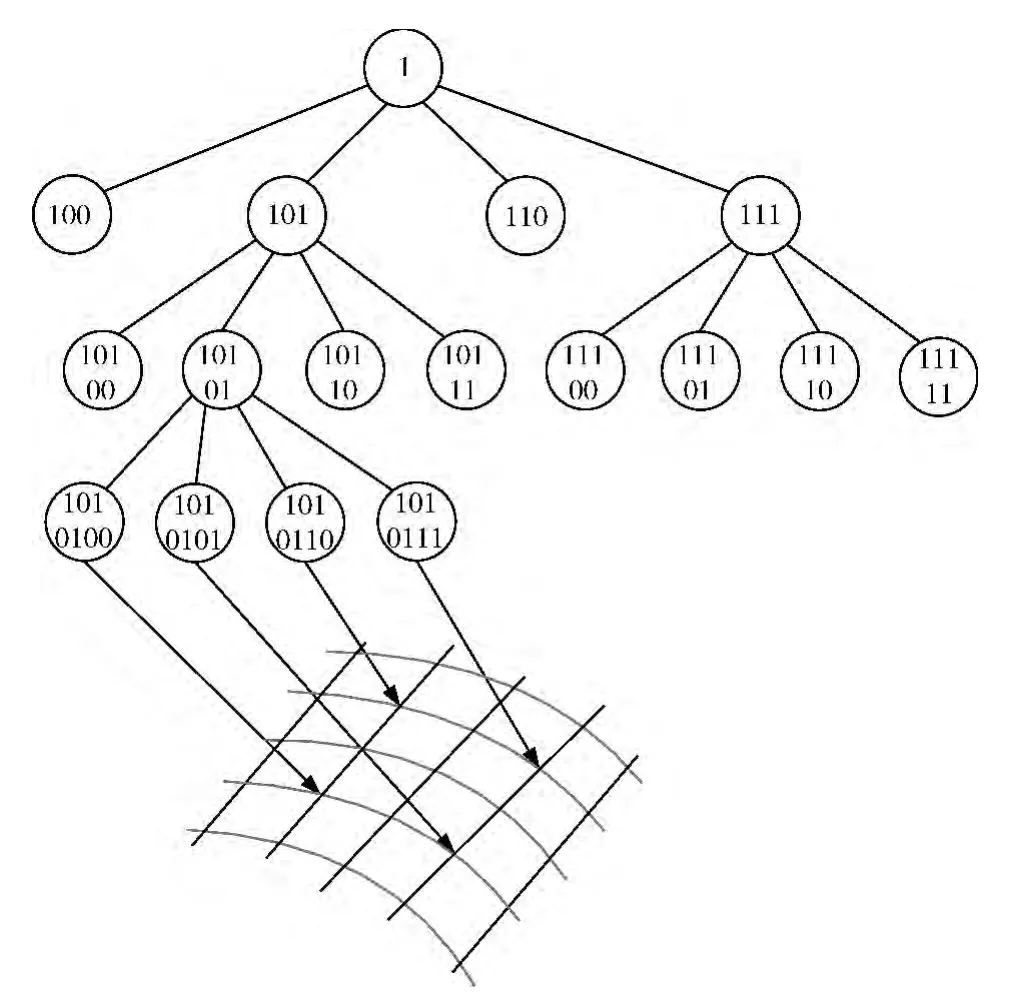
图3 曲面四叉树结构
曲面层四叉树按后序遍历方式生成,即按后序遍历方法逐步合并子曲面,得到一个四叉树结构的曲面表示方式,以根指针作为标识。实体模型的多个子NURBS曲面相互关联,可视化时通过后序遍历四叉树方式逐步重绘整个曲面。
3 实验结果与分析
为了验证方法的正确性和有效性,对不同的点云模型进行了实验验证。模型系统以Visual C++6.0 为开发环境,使用了OpenGL 图形开发包。图4是根据点云数据dinosaurs重构的结果。针对Bunny、Mannequin、Dragon 和Cow 等4个模型,表1给出了本文算法与传统Delaunay算法在重构速度方面的比较结果。
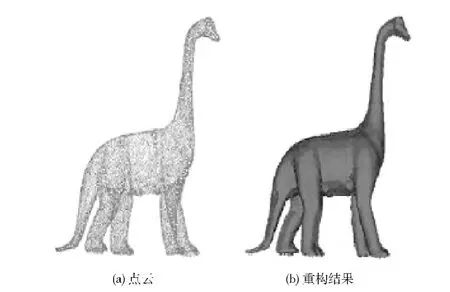
图4 实验结果
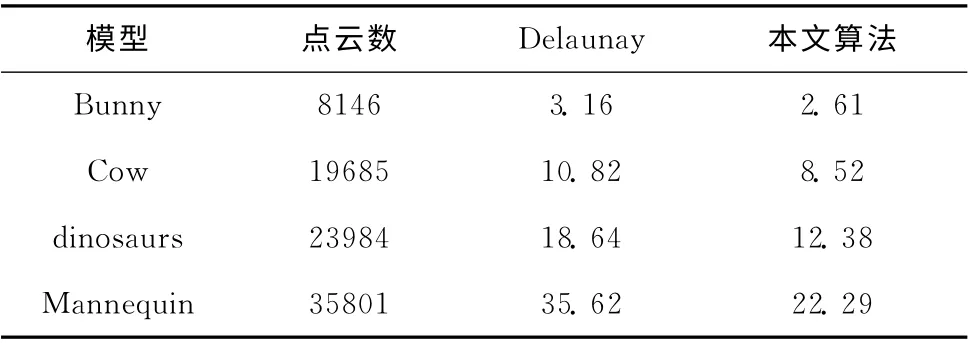
表1 重构时间比较/s
实验结果表明,对于一般的点云模型,本文算法比传统的Delaunay算法在效率上可以提高10%~15%;对于较复杂的点云模型,重构效率可以提高50%左右。算法效率较高,重构效果较好,比较适合三维实体的实时绘制,适用于大数据量数据的表面重建。在处理不规则的实体时,在相同分辨率的前提下,混合模型的数据存储空间比Delaunay模型少30%左右。
4 结束语
曲面重构在多个领域得到了应用,针对散乱点云的曲面重构方法仍然需要进一步研究。在对三维建模理论和方法进行深入研究的基础上,提出了一种基于八叉树空间分割的NURBS曲面重构方法。模型采用混合八叉树和四叉树的数据结构,利用八叉树划分、精简三维实体的点云数据,并建立八叉树与四叉树的链接,减少了数据模型的存储空间。重构算法避免了复杂曲面拼接的计算复杂度,可以过滤掉对重构效果影响不大的数据点,并避免了法向一致化的复杂计算。相比传统的Delaunay算法,本文算法在重构效率方面有较大的改进,模型可以用于实体的三维可视化。但对复杂模型的可视化,仍存在边缘效应,算法还需要改进。今后的工作是将算法与极小曲面造型方法结合,进一步提高重建的精确性。
[1]MA H C,Wang Z Y.Distributed data organization and parallel data retrieval methods for huge laser scanner point clouds[J].Computers &Geosciences,2011,37 (2):193-201.
[2]FU Huan,LIANG Li,WANG Fei,et al.A point cloud segmentation algorithm using local convexity and octree[J].Journal of Xi’an Jiaotong University,2012,46 (10):60-65 (in Chinese).[傅欢,梁力,王飞,等.采用局部凸性和八叉树的点云分割算法 [J].西安交通大学学报,2012,46 (10):60-65.]
[3]Bai Y,Han X,Prince J L.Digital topology on adaptive octree grids[J].Journal of Mathematical Imaging and Vision,2009,34 (6):165-184.
[4]GONG Jun,KE Shengnan,ZHU Qing,et al.An efficient management method for point cloud data based on Octree and 3D R-tree[J].Acta Geodaetica ET Cartographica Sinica,2012,41 (4):597-604 (in Chinese). [龚俊,柯胜男,朱庆,等.一种八叉树和三维R 树集成的激光点云数据管理方法 [J].测绘学报,2012,41 (4):597-604.]
[5]Lewiner T,Mello V,Peixoto A.Fast generation of pointerless octree duals [J].Journal Compilation,2010,29 (5):1661-1669.
[6]Wang M,Tseng Y H.Incremental segmentation of lidar point clouds with an octree-structured voxel space [J].The Photogrammetric Record,2011,26 (133):32-57.
[7]WU Jun,YANG Jie.QIN Hongxing.Incremental surface reconstruction of unorganized points based on BFS [J].Journal of Shanghai Jiaotong University,2008,42 (10):1740-1744(in Chinese).[伍军,杨杰,秦红星.基于广度搜索的增量式点云表面重建 [J].上海交通大学学报,2008,42 (10):1740-1744.]
[8]SHAO Zhengwei,XI Ping.Data reduction for point cloud using octree coding [J].Journal of Engineering Graphics,2010,31 (4):73-76 (in Chinese).[邵正伟,席平.基于八叉树编码的点云数据精简方法 [J].工程图学学报,2010,31(4):73-76.]
[9]GAO Xiangmin,PANG Mingyong.Incremental mesh reconstruction from unorganized points [J].Journal of Chinese Computer Systems,2011,32 (10):2096-2011 (in Chinese).[高向敏,庞明勇.散乱点云的快速增量网格重建算法 [J].小型微型计算机系统,2011,32 (10):2096-2011.]
[10]Chen S Y,Guan Q.Parametric shape representation by a deformable NURBS model for cardiac functional measurements[J].IEEE Transactions on Magnetics,2011,58 (3):480-487.
[11]Jagannathan A,Miller E L.Three-dimensional surface mesh segmentation using curvedness-based region growing approach[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29 (12):2195-2204.
[12]WANG Xiaoming,LIU Jixiao.A new approach of adaptive compression and mesh generation for large scale scattered data[J].Journal of Engineering Graphics,2010,31 (2):92-95(in Chinese).[王晓明,刘吉晓.一种大规模散乱数据自适应压缩与曲面重建方法 [J].工程图学学报,2010,31 (2):92-95.]
[13]LIANG Qunxian,XU Hongli.A fast method of curved surface reconstruction based on point cloud data [J].Computer Engineering,2013,39 (2):237-240 (in Chinese). [梁群仙,许宏丽.一种基于点云数据的快速曲面重构方法 [J].计算机工程,2013,39 (2):237-240.]
[14]NIE Jianhui,MA Zi,HU Ying,et al.Rapid surface reconstruction algorithm from dense point cloud [J].Journal of Computer-Aided Design & Computer Graphics,2012,24(5):574-582 (in Chinese).[聂建辉,马孜,胡英,等.针对密集点云的快速曲面重建算法 [J].计算机辅助设计与图形学学报,2012,24 (5):574-582.]

