基于SUMTNSGA－II的多目标轨迹规划

杨 云，周 诚，王 崴，2，彭勃宇

（1.空军工程大学 防空反导学院，陕西 西安710051；2.西安交通大学 机械制造系统工程国家重点实验室，陕西 西安710049）

0 引 言

出于训练吊机操作手的需要，研发出基于虚拟现实的吊机训练系统。为校验路径合理性、避免吊机振动、延长关节使用寿命，设计出吊机吊装过程中最优路径，以便作为参考，加速操作手熟练掌握吊机操作要领。吊机吊装路径的优化问题，本质上属于机械臂轨迹优化问题。

针对轨迹规划，国内外学者提出了许多独到的见解。文献 ［1－3］考虑时间、能量等单一方面因素，忽略其它因素影响，在特定环境下具有优势，但是针对吊机工作环境产生的轨迹不能令人满意；文献 ［4，5］分别以时间、脉动和时间、能量最优结合作为目标函数，对机械手关节进行轨迹规划，所求结果较单目标优化相比有所提升；文献［6］运用7次B样条曲线确保了关节启、止时刻速度、加速度、脉动可设定，但是高阶样条曲线的运用导致计算过程复杂，求解困难；文献 ［4－6］处理约束化问题采用加权系数将多目标函数转化为单目标问题，这种方法若权重分配不合理，将会影响求解结果，同时无法获得多组可行解，不能保证所得解为全局最优解；文献 ［7］提出了采用改进非支配排序遗传算法对机械手轨迹进行优化，有效地实现了多目标寻优，得到了理想的Pareto分布，但算法效率还有提升空间；文献 ［8］提出了利用层次分析法 （AHP）的优化算法，该方法首先通过最优时间轨迹规划得到最优时间，然后在最小时间内进行最优冲击规划，这种方法有一定可行性，但是算法求解范围有限，易陷入局部最优导致中断现象。

本文充分考虑吊机工作环境中时间、能量、冲击等因素，采用5次非均匀B 样条曲线在关节空间插值保证轨迹平滑，提高轨迹平稳性，改善冲击，减小振动。对于约束化问题使用基于改进带精英策略的遗传算法 （SUMTNSGA－II）进行求解，从而规划出满足各约束条件的最优轨迹，得到多组Pareto解，从中选取全局最优解。

1 吊臂模型建立

吊机吊臂三维模型结构如图1 所示，它由基柱底座、大臂回转轴、小臂回转轴、伸缩臂、吊具摆动轴和末端抓手构成，具有6个自由度。D－H 坐标系如图2所示。

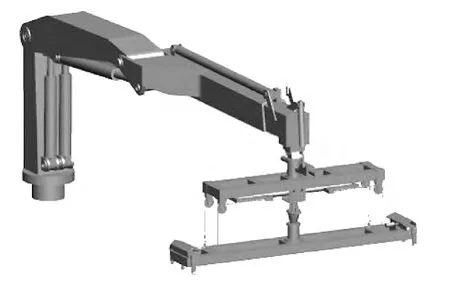
图1 吊机三维模型

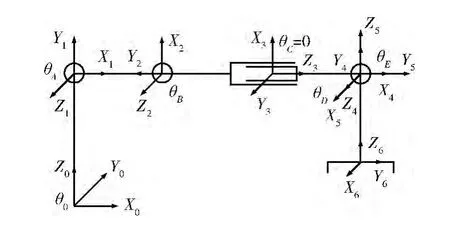
图2 吊臂D－H 坐标系

吊机工作时基柱底座可自由旋转，大臂回转轴带动小臂回转轴完成俯仰联动，伸缩臂只能进行平移运动，吊具末端抓手在回转轴和吊具摆动轴作用下完成旋转和俯仰用以抓取集装箱。

2 最优轨迹规划问题描述

2.1 五次非均匀B样条曲线轨迹规划

由于吊机不需要设定启停时刻各参数，故采用5次非均匀B样条曲线在关节空间插值保证轨迹平滑，由非均匀B样条曲线通式求解n＋1个5次非均匀B样条曲线方程

式中：ti（u）、θi（u）——i段曲线的横、纵坐标。且B样条曲线基函数系数阵N5、控制顶点阵Dj，i分别为

由德布尔递推公式得到B 样条曲线的一阶、二阶、三阶导数为

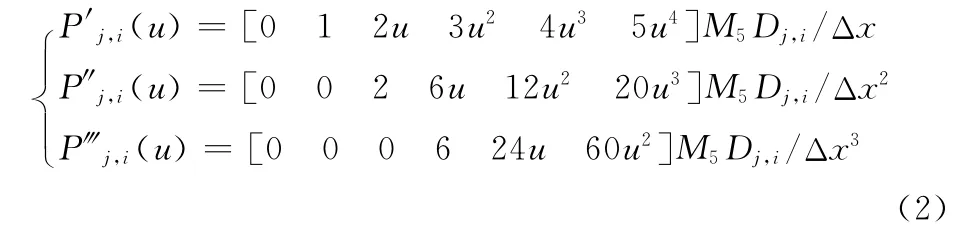
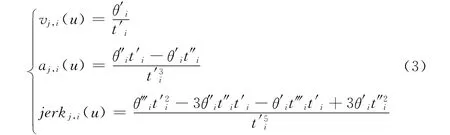
同理，关节第i段曲线的速度、加速度和脉动函数

为了保证轨迹经过特定的位置点，首先反求B 样条插值轨迹曲线的控制顶点。联立方程 （1）～方程 （3），可求解插值曲线的控制顶点，方程描述为

式中：Aj——系数阵，dj、pj满足方程

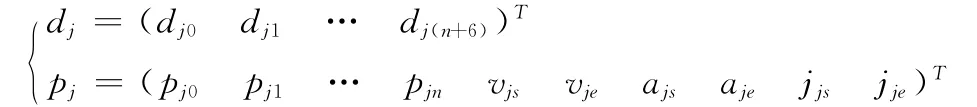
再由式 （4）反解出关节控制顶点

2.2 目标函数与约束条件

为提高吊臂作业效率、降低能耗、保护吊臂关节、减少关节振动、延长吊臂使用寿命。预设期望目标吊臂工作时间最短、能耗最少、轨迹平滑性最好。目标函数定义如下

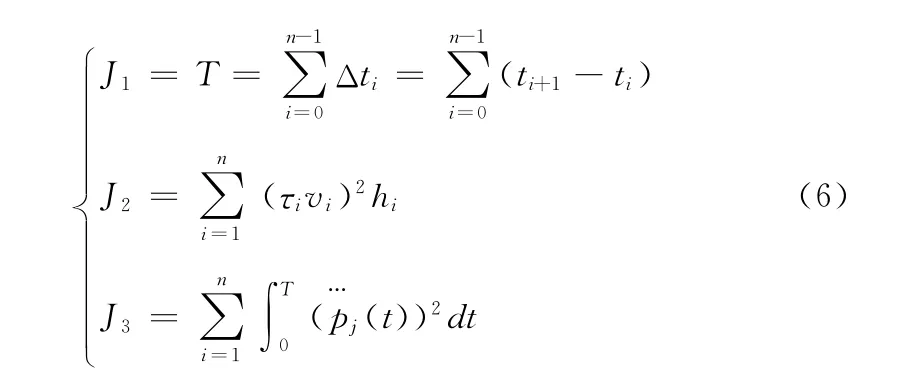
式中：J1——吊臂时间目标函数，为吊臂工作时间；J2——吊臂能量消耗目标函数，τ——吊臂控制力矩；J3——关节冲击［9］，Pj（t）——关节j在时刻t经过位置pi的连续关节轨迹。

与关节m 的运动学约束对应的控制顶点约束满足

联立式 （6）～式 （7）可以得到非线性约束的标准形式为

3 SUMTNSGA－II算法描述

3.1 SUMTNSGA－II算法

文献 ［10］提出的基因环境双演化免疫克隆算法采用了约束处理策略，在优化过程中使用约束处理策略对目标函数进行修正，弱化了由于约束限制而产生的可行解集的限制。其惩罚函数写为

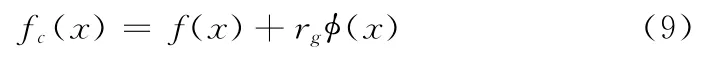
式中：rg——惩罚系数，（x）——惩罚项。这种定义惩罚函数的方法存在不足之处。首先惩罚系数以及惩罚项形式的选取易受人为影响，如选取不适将影响寻优过程，严重时将会漏掉某些非支配解集。其次，对于多目标问题，由于目标轻重不同，每个目标的惩罚项不都相同，常规惩罚函数无法面面俱到。

针对以上问题，本文采用基于修正带精英策略的遗传算法对目标函数进行优化，在优化过程中首先使用惩罚函数法 （SUMT）［11］对目标函数进行修正，并从修正后的目标函数值中选取一定解集作为父代，进行进化。同时，利用精英存储策略预存一个精英种群，储存杂交变异中非支配可行解。最后对群体进行迭代操作，迭代过程一般包括3个主要步骤：选择操作 （select operation）、杂交操作（crossover operation）、变异操作 （mutation operation），以便保持解集活性。此法优点为：首先在解集选择中，既保留了可行解，又保留了在约束之外，但偏离目标函数值较小的非可行解；其次，针对不同层次目标函数实现不同的惩罚代价，有效地改善解集的多样性、均匀性。

3.1.1 计算惩罚函数

改进后目标函数为

式中：f（x）——原目标函数，ri（x）——个体x 的第i 维目标函数距离值，rg——加权因子，Ωi（x）——个体x 的第i维惩罚项，fi（x）——个体x 修正后第i 个目标函数。具体计算过程为

（1）距离项计算

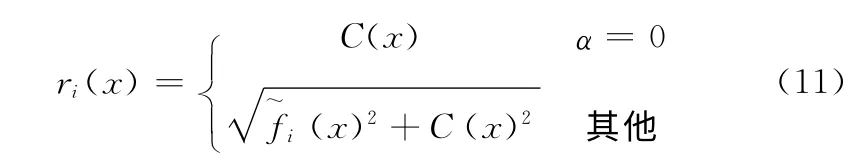
式中：C（x）——目标函数约束偏离值，α——可行解在种群中所占比例，f ～i（x）——目标函数归一化值，参数计算过程为

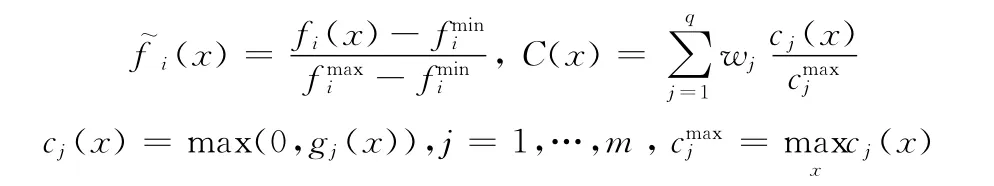
式中：fmini、fmaxi——目标函数i的最小值和最大值，g（x）——约束。

（2）惩罚项计算

式中：C′（x）——约束偏离度修正值，表示为

联立式 （10）～式 （13），当α为零时，即种群中无可行解，由式 （12）可知Ω（x）为0，此时仅依靠r（x）对目标函数进行改进。当0＜α＜0.5时，即种群中非可行解所占比例较高，则罚函数Ω（x）对于约束惩罚较重，有利于解集进化；当α＞0.5 时，即种群中可行解所占比例较大，则r（x）对目标函数惩罚较重，有利于个体向最优解进化。

3.1.2 选择操作

（1）可行非支配解选取：首先选取子代种群中可行解集，然后将父代非支配解集中的可行非支配解复制到子代可行解集中。根据每个个体目标函数值在可行解集内选取可行非支配解集。

（2）罚函数非支配解选取：与可行非支配解集选取相似，只是将目标函数变为修正后目标函数—罚函数。

（3）复制非支配解集：复制非支配解集是保持种群多样性的重要环节，计算方式为将父代非支配解集进行n 次复制。此法与NSGA－II相比，有以下优点：

1）略去了群体中非支配排序和拥挤度计算，降低计算复杂度。

2）由于对可行非支配解集的复制会导致解集规模大幅度扩大，加重选择操作负担。于是仅对非支配解集进行n倍复制操作，这样减少选择耗时，加快算法求解效率。

3.2 算法描述

步骤1 初始化种群，设置进化代数计数器G＝0；采用全局随机取样机制产生各子群体的第一代初始种群，规模为n；

步骤2 计算目标函数值、约束偏离度值；

步骤3 计算修正后目标函数值；

步骤4 选取可行非支配解集；

步骤5 选取非可行解集；

步骤6 交叉、变异；

步骤7 判断是否为第一代种群，如果是执行步骤8，如果不是跳转步骤4；

步骤8 父、子代解集合并；

步骤9 复制非支配解集；

步骤10 判断是否为新一代种群，如果是执行步骤11，如果不是跳转步骤9；

步骤11 选择、杂交、变异；

步骤12 判断是否达到最大迭代次数，如果是，输出结果，如否，迭代次数加1，跳转步骤10。

4 仿真结果

SUMTNSGA－II算法参数包括：种群总大小N ＝300，交叉概率为0.9，交叉分布指数为15，变异概率为0.1，变异分布指数为20，最大的可行非支配解集大小为150，修正的非支配解集大小为150。

吊机工作时各关节速度、加速度、二次加速度、力矩约束见表1。

表1 各关节约束

由表2可以得知，SUMTNSGA－II算法在一次运行中能够得到多组Pareto解，充分验证了该算法的多样性、均匀性及较快的收敛速度。为获得相对最满意的解，考虑到吊臂模型目标函数重要程度，以时间重要性最高，能耗次之，关节冲击最低，选取序号9作为本次实验最满意解。

对比实验结果可以看出，解集多样性较文献 ［3－5］明显提高，能够得到任意权值下多组有效解集。同序列二次规划 （SQP）［6］相比最优时间优势不明显，但是耗能更少，冲击更小，更有利于保护关节，避免损伤；与INSGA－II算法［7］最优时间减少3.0334s；与层次分析法 （AHP）［8］相比时间、能量优化不明显，但关节冲击明显减少。

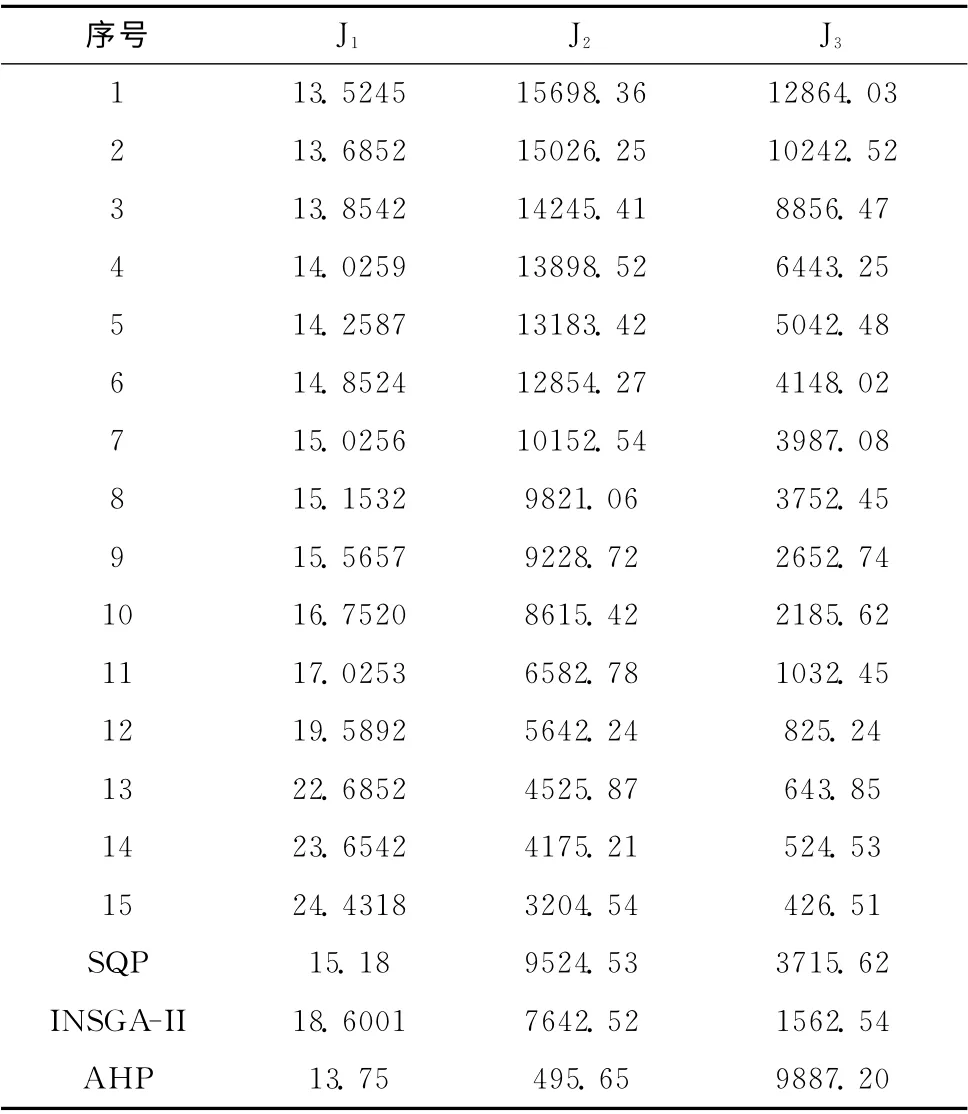
表2 吊臂多目标优化结果

图3为序号9条件下各个关节速度、加速度、二次加速度优化结果。

5 结束语

本文运用五次B样条曲线对吊机工作运动轨迹进行规划，改善吊臂速度、加速度、二次加速度，使运动更加平缓。综合考虑运动过程中时间、能量和冲击等因素，针对约束化问题采用一种改进的SUMTNSGA－II算法求解，通过实验验证了算法的有效性，能够得到多组Pareto分布，求得最优解。

下一步研究工作是将提出的最优轨迹应用于虚拟吊机训练系统，将最优路径作为参考标准检验操作员吊装路径，加速操作员训练过程。

［1］WANG Panfeng，MEI Jiangping，HUANG Tian.Time optimal path planning of a 2－D of high－speed parallel robot ［J］.Journal of Tianjin University，2007，40 （10）：1139－1145 （in Chinese）.［王攀峰，梅江平，黄田.高速并联机械手抓放操作时间最优轨迹规划 ［J］.天津大学学报，2007，40 （10）：1139－1145.］

［2］LI Dongjie，QIU Jiangyan，YOU Bo.Optimal algorithm for trajectory planning of the robot ［J］.Electric Machines and Control，2009，13 （1）：123－127 （in Chinese）.［李东洁，邱江艳，尤波.一种机器人轨迹规划的优化算法 ［J］.电机与控制学报，2009，13 （1）：123－127.］

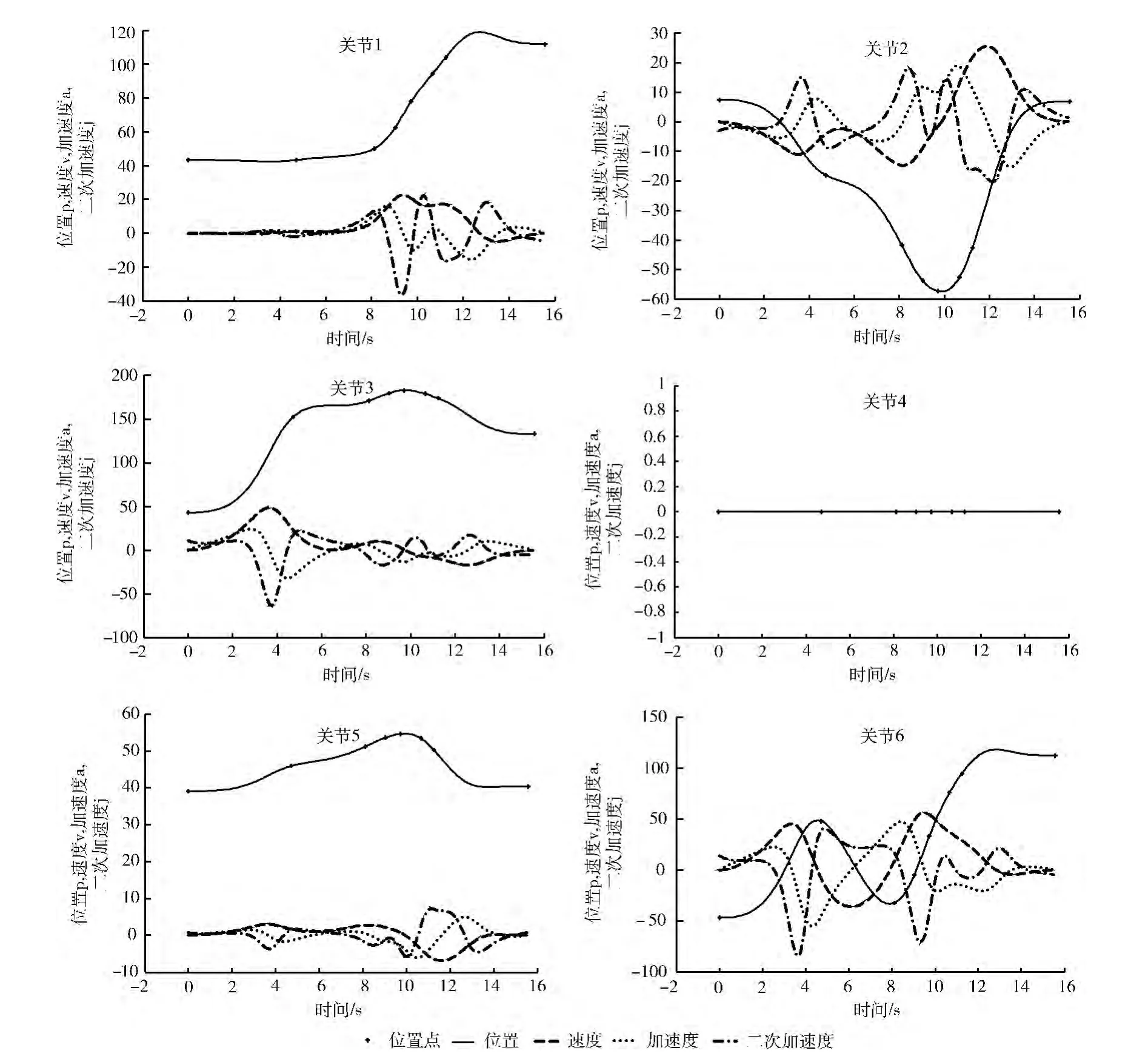
图3 最优轨迹仿真

［3］Pérez Bailón W，Barrera Cardiel E，Juárez Campos I.Mechanical energy optimization in trajectory planning for six DOF robot manipulators based on eighth－degree polynomial functions and a genetic algorithm ［C］／／7th International Conference on Electrical Engineering，Computing Science and Automatic Control，2010：8－10.

［4］Liu Huashan，Lai Xiaobo，Wu Wenxiang.Time－optimal and jerk－continuous trajectory planning for robot manipulators with kinematic constraints ［J］.Robotics and Computer－Integrated Manufacturing，2013，29 （2）：309－317.

［5］Gasparetto A，Zanotto V.Optimal trajectory planning for industrial robots［J］.Advances in Engineering Software，2010，41 （4）：548－556.

［6］ZHU Shiqiang，LIU Songguo，WANG Xuanyin，et al.Timeoptimal and jerk－continuous trajectory planning algorithm for manipulators［J］.Journal of Mechanical Engineering，2010，46 （3）：47－52 （in Chinese）.［朱世强，刘松国，王宣银，等.机械手时间最优脉动连续轨迹规划算法 ［J］.机械工程学报，2010，46 （3）：47－52.］

［7］WANG Huifang，ZHU Shiqiang，WU Wenxiang.INSGA－Ⅱbased multi－objective trajectory planning for manipulators ［J］.Journal of Zhejiang University （Engineering Science），2012，46 （4）：622－628 （in Chinese）. ［王会方，朱世强，吴文祥.基于INSGA－Ⅱ算法的机械手多目标轨迹规划 ［J］.浙江大学学报 （工学版），2012，46 （4）：622－628.］

［8］YU Yang，LIN Ming，LIN Yongcai.Optimal trajectory planning for industry robot based on hybrid genetic algorithm ［J］.Computer Engineering and Design，2012，33 （4）：1574－1580 （in Chinese）.［余阳，林明，林永才.基于混合遗传算法的工业机器人最优轨迹规划［J］.计算机工程与设计，2012，33 （4）：1574－1580.］

［9］CAO Zhongyi，WANG He，WU Wanrong，et al.Time－jerk optimal trajectory planning of shotcrete manipulators［J］.Jour－nal of Central South University （Science and Technology），2013，44 （1）：114－121 （in Chinese）. ［曹中一，王鹤，吴万荣，等.喷浆机械手时间最优与脉动最优轨迹规划 ［J］.中南大学学报 （自然科学版），2013，44 （1）：114－121.］

［10］XU Haili，XIE Xiangrong，ZHUANG Jian，et al.Global time－energy optimal planning of industrial robot trajectories［J］.Journal of Mechanical Engineering，2010，46 （9）：19－25 （in Chinese）.［徐海黎，解祥荣，庄健，等.工业机器人的最优时间与最优能量轨迹规划 ［J］.机械工程学报，2010，46 （9）：19－25.］

［11］BAO Jianghong.Solution multiple－choice knapsack problem using penalty function method implemented by genetic algorithm ［J］.Computer Engineering and Design，2008，29（17）：4518－4524 （in Chinese）. ［鲍江宏.用遗传算法实现罚函数法解多选择背包问题 ［J］.计算机工程与设计，2008，29 （17）：4518－4524.］