基于KL变换和RLS的彩色图像平滑滤波

史崇升，安慧慧，汤全武，张忠旺

（1.中国电信股份有限公司宁夏分公司，宁夏 银川750002；2.中国人寿保险股份有限公司宁夏分公司，宁夏 银川750002；3.宁夏大学 物理电气信息学院，宁夏 银川750021）

0 引 言

彩色图像平滑滤波技术［1］主要可分为标量滤波法和矢量滤波法，标量滤波法在彩色图像的每个通道上独立地进行滤波，而矢量滤波法把彩色图像每个像素作为一个矢量［2］。在标量滤波法方面，杨文兵等［3］基于HSI彩色空间对图像进行平滑，能够有效消除图像噪声影响；张闯等［4］针对彩色图像双边滤波去噪方法存在的不足，提出一种边缘检测与双边滤波相结合的彩色图像去噪方法。在矢量滤波法方面，李雪威等［5］通过确定初始高斯模板和高斯权值矩阵，实现对图像的平滑；王晏等［6］根据图像的颜色信息分布定义权重函数，求取自适应空域带宽，结合图像颜色信息、评价图像质量的频域结构相似度，并且通过最小化局部方差和最大化图像频域结构相似度确定了值域带宽，采用Mean Shift算法克服了图像过平滑问题，取得了较好的结果；邓廷权等［7］提出一种彩色图像自适应中心加权的矢量中值滤波方法，实验验证了该方法能有效去除彩色图像的椒盐噪声；马义德等［8］对污染严重的图像，提出了自适应彩色图像SCM 去噪方法，结果表明去噪后的主观视觉和客观评价明显有所改善；陈北京等［9］为了整体处理彩色图像，提出了一种基于四元数的去除泊松噪声的加权平均滤波器。

在上述彩色图像平滑滤波方法中，主要涉及对彩色图像的平滑或去噪，研究对象为被噪声处理的彩色图像，而本文提出的结合KL 变换与递推最小二乘法RLS的平滑滤波算法是对模糊且添加噪声的RGB 彩色图像进行平滑滤波。该算法利用离散KL变换将模糊加噪的RGB彩色图像转至新的彩色空间，并对各分量利用RLS平滑滤波，再将去噪的分量图像合成并进行离散KL 逆变换，得到平滑滤波图像。实验结果表明，该算法具有较好的抑制高斯噪声和椒盐噪声的效果，能够提高模糊图像的质量。

1 基于KL变换和RLS的彩色图像平滑滤波

1.1 彩色图像的KL变换

一幅彩色图像就是彩色像素M×N×3的数组，其中每一个彩色像素点都是在特定空间位置的彩色图像相对应的3个分量，可以看成是一个由3幅灰度图像形成的 “堆”，即R、G、B这3幅灰度图像［10］。令向量X 表示该彩色图像，则X 的表达式为

X 向量的协方差矩阵定义为

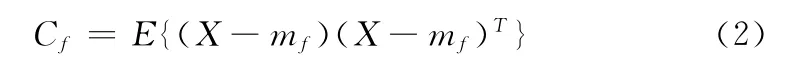
式中：E——求期望；T——求转置；mf——平均向量，mf的定义式为

将式 （3）代入式 （2）可知Cf是一个3×3的实对称矩阵，故可找到它的一组3个正交特征值。令λi（i＝1，2，3）是按递减顺序排列的协方差矩阵的特征值；ei（i＝1，2，3）是协方差矩阵的特征向量。则定义KL变换矩阵T 为

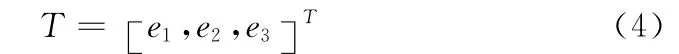
KL变换的表达式为

式中：X－mf——原始图像向量X 减去平均值向量mf，称为中心化图像向量。此式表明，变换后的图像向量Y 等于中心化图像向量X－mf与变换矩阵T 相乘。变换后的图像向量Y 的均值向量my＝0，则向量Y 的协方差矩阵Cy＝TCfTT，可证明协方差矩阵Cy是对角型矩阵，其对角线上的元素等于Cf的特征值λi（i＝1，2，3），即

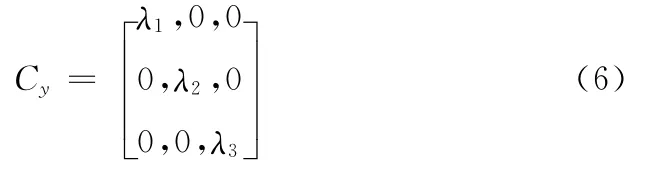
Cy非对角线上的元素为0，说明变换后向量Y 的像素是不相关的。将RGB图像利用KL 变换后，原彩色图像X 将转化为图像Y ，向量Y 3个分量 （J、K、L），即RGB彩色空间转为JKL 彩色空间。向量Y 的表达式为

KL逆变换的表达式为

1.2 自适应RLS滤波算法

递推最小二乘法 （recursive of least square，RLS）是FIR 维纳滤波器的一种时间递归算法。RLS 的基本思想：新的估计值在老的估计值基础上修正而成的［11］。

根据参考文献 ［12］，设θ为一向量，且θ仅与当前观测值有关，则新的估计值＝老的估计值＋修正项，推导可得最小二乘递推算法的形式为

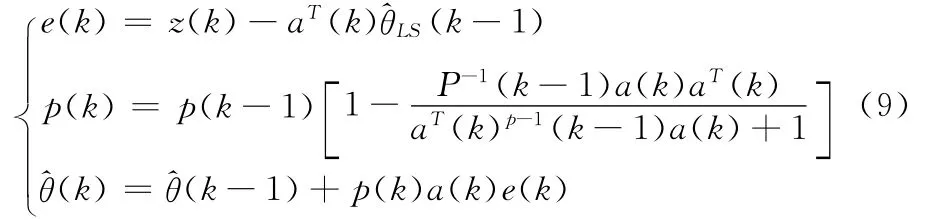
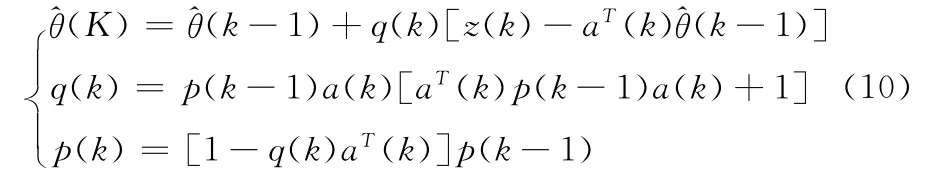
递推最小二乘的另一种形式为

式中：p（k）、q（k）——定义的中间变量；z（k）——k 时刻期望信号；a（k）——k时刻输入信号。

式 （10）只适用于一维信号的处理，若要对式 （7）的J、K、L分量进行滤波，就必须在滤波算法程序设计过程当中设计两层嵌套循环，对二维图像J、K、L 各分量分别逐行扫描或逐列扫描，以实现用RLS算法对J、K、L 三分量的滤波去噪。

2 KL－RLS平滑滤波算法

2.1 算法的基本思想

该算法首先对待平滑的彩色图像进行离散KL 变换，去除R、G、B各分量间的相关性，将其RGB 空间转换为JKL空间 （J、K、L 分量均值为零，互不相关，并且方差依次增大）。然后分别对J、K、L分量分别采用递推最小二乘滤波算法RLS滤波，并将滤波的分量图像合成为JKL 空间图像。最后将合成的图像进行离散KL 逆变换，得到最终的平滑滤波图像。为了叙述的方便，将本文对彩色图像的滤波算法称为KL－RLS平滑滤波算法，具体实现算法的流程如图1所示。

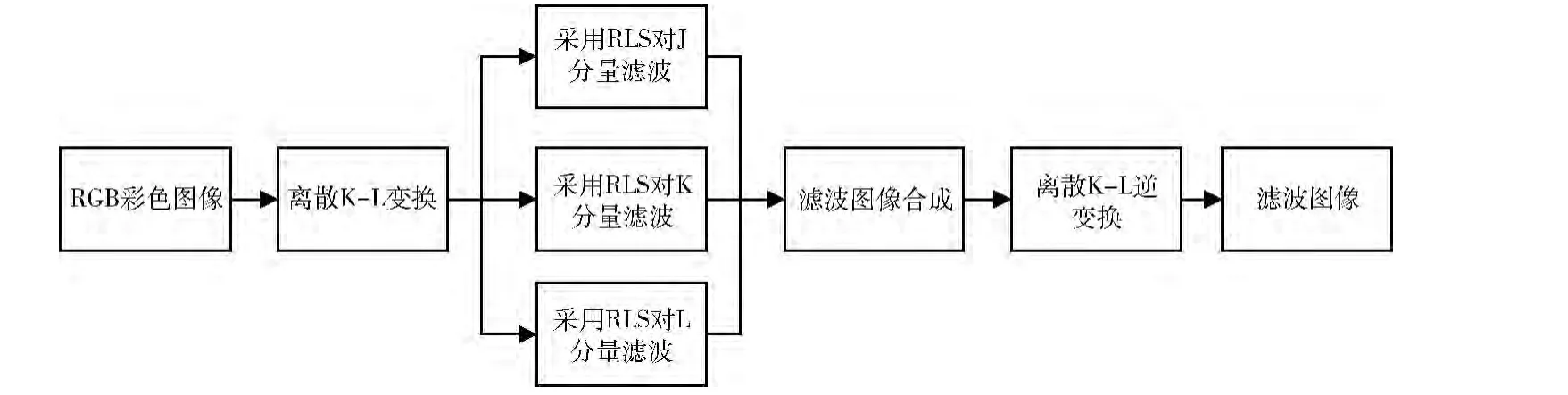
图1 KL－RLS平滑滤波流程

2.2 评价标准

本文采用均方误差 （MSE）、峰值信噪比（PSNR）值和相关测度K［13］作为彩色图像平滑滤波结果的客观评价标准。

均方误差MSE用来表示平滑滤波图像与原始图像之差平方的期望值，其离散形式为

式中：f（x，y）、g（x，y）——原始图像的分量、平滑滤波图像的分量在点（x，y）上的灰度值，M、N——x 方向、y 方向图像像素点的个数。

峰值信噪比PSNR 反映平滑滤波图像的失真程度，一般它的值越大就表示平滑滤波图像的质量越好，其定义为

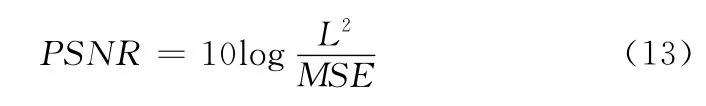
式中：L——平滑滤波图像分量的灰度取值范围。

相关测度K 值即表示平滑滤波图像的分量和原始图像分量的相似程度，其定义为

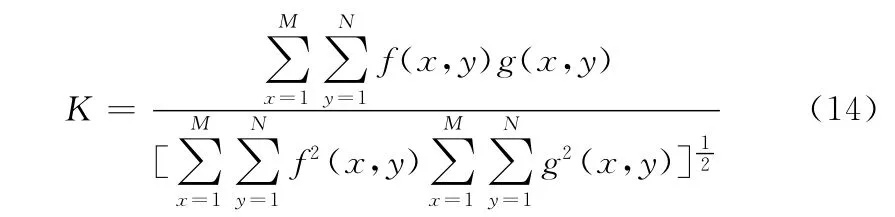
整幅图像的均方误差MSE、峰值信噪比PSNR 值和相关测度K 值取R、G、B三通道的均值。

3 仿真实验与结果分析

3.1 实验安排

实验选用的图像特征为8 位无符号整形Lena 图像，PNG 格式，尺寸256x256，如图2 （a）所示。实验内容分为两部分：①对输入的RGB图像模糊且加入不同的噪声类型，包括高斯噪声和椒盐噪声，采用KL－RLS平滑滤波算法进行滤波，并利用均方误差MSE、峰值信噪比PSNR 值和相关测度K 值对本文算法客观的分析评价；②采用常数比率的维纳滤波、自相关函数的维纳滤波对模糊加噪的Lena进行滤波，并与KL－RLS平滑滤波的效果相比较。其流程如图3所示。

3.2 实验结果与分析

图2 KL－RLS平滑滤波算法的滤波效果

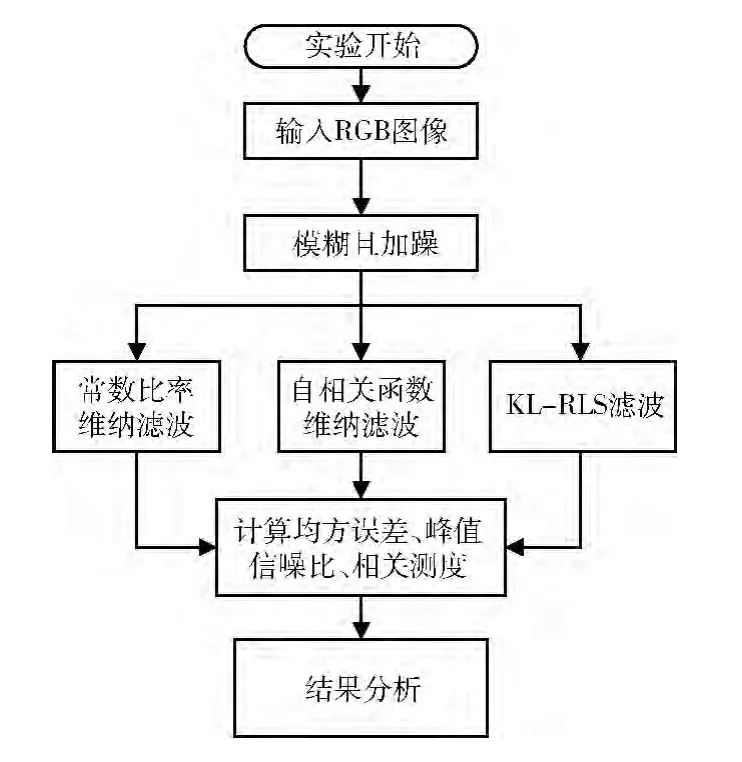
图3 实验流程

图像模糊是由场景和传感器两者产生的，或者是在图像获取时传感器和场景之间的均匀线性运动而产生，为了模拟这种情况，可以使用IPT 函数fspecial（参数选择motion、len、theta，参数theta以度为单位，以顺时针方向对正水平轴度量），近似于由有着len个像素的摄像机的线性移动的效果，并通过添加适当的噪声对图像模糊建模。对图2 （a）使用fspecial函数模糊，其参数len为7，theta为45度。当加入均值为0，方差为0.01的高斯噪声，效果如图2 （b）所示，并采用KL－RLS平滑滤波，平滑结果如图2 （c）所示；对图2 （a）加入噪声密度为0.05 的椒盐噪声，效果如图2 （d）所示，同样也采用KL－RLS平滑滤波，平滑结果如图2 （e）所示。

从图2可以看出：使用KL－RLS平滑滤波算法对模糊加噪的Lena图像滤波，对高斯噪声和椒盐噪声均具有良好的抑制作用，达到了较好的滤波效果，其滤波结果均能较为清晰的看到Lena图像的边缘和细节信息，但会产生一定的颜色失真。

图4 （a）～图4 （c）是对模糊的Lena图像添加高斯噪声，并经过离散KL 正变换后的J、K、L 分量图像，从中可看到J分量图像完全被淹没在噪声之中；K 分量图像可看到Lena的边缘和轮廓；L分量图像明显要比J分量和K分量清晰。图4 （d）～图4 （f）是对J、K、L 各分量滤波后的图像，与经过离散KL正变换的分量图像相比，J分量依然看不清图像的轮廓，可Lena右侧的背景轮廓大致可以看到；K 分量和L分量图像明显的消除了噪声的影响。因此，说明采用自适应RLS滤波算法对经过离散KL正变换后的J、K、L分量滤波，可获得了较好的平滑滤波效果。表1计算的MSE、PSNR、K值可进一步说明这一直观判断。

图4 J、K、L分量滤波前后的图像

表1 J、K、L分量滤波前后的MSE、PSNR、K值

从表1可看出，经过离散KL 正变换的各分量与模糊且添加高斯噪声R、G、B 各分量之间的MSE、PSNR、K值相比，对J、K、L 分量采用RLS滤波之后，J－R、K－R、L－B的PSNR、K 值较大且MSE 值较小，说明对KL 变换的分量图像采用自适应RLS滤波算法后，提高了J、K、L各分量图像的质量。对模糊的Lena图像添加椒盐噪声，也可得到相同的结果。

采用常数比率的维纳滤波、自相关函数的维纳滤波对添加高斯噪声、椒盐噪声的Lena模糊图像进行滤波，结果如图5 （a）～图5 （d）所示。

将图2 （c）、图2 （e）与图5相比较可知：①采用KLRLS平滑滤波算法，可以提高图像的视觉效果和图像的质量，而采用常数比率维纳滤波、自相关函数维纳滤波算法虽然可以较为清晰的看到Lena的边缘和轮廓等细节信息，但图像的噪声依然很大，并且存在颜色失真；②与采用常数比率维纳滤波算法相比，自相关函数维纳滤波对模糊加噪图像的滤波效果较为明显。表2、表3、表4是各滤波算法的MSE、PSNR、K 值。

图5 常数比率维纳滤波、自相关函数维纳滤波算法的滤波效果

表2 KL－RLS平滑滤波算法的MSE、PSNR、K 值 （模糊高斯噪声）

表3 KL－RLS平滑滤波算法的MSE、PSNR、K 值 （模糊椒盐噪声）

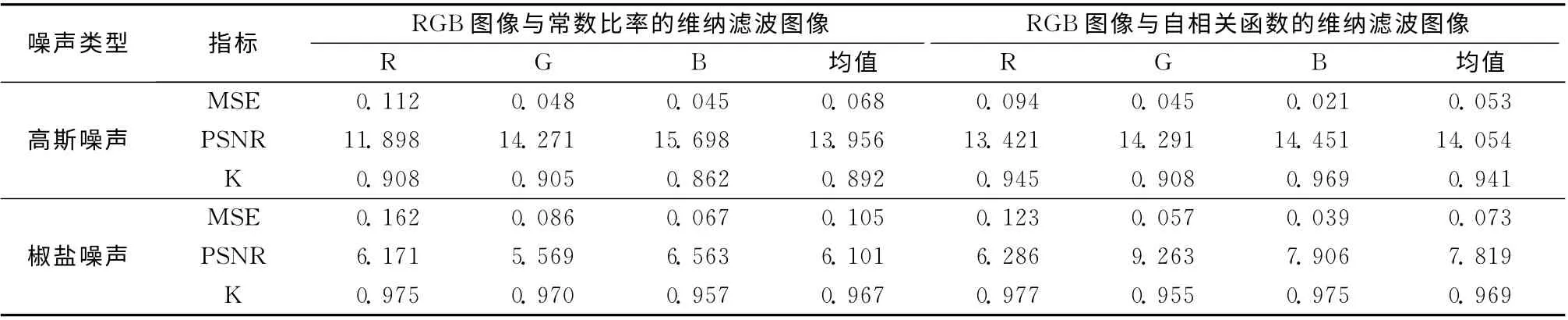
表4 常数比率维纳滤波、自相关函数维纳滤波算法的MSE、PSNR、K 值

从表2和表3可以看出：①同RGB图像与其模糊加噪图像之间的MSE、PSNR、K 值相比，原始Lena图像与直接经过KL变换的重构图像之间的PSNR、K 值均较小且MSE值较大，说明模糊加噪的RGB图像直接采用KL变换得到重构图像，没有提高RGB 图像的质量；②同RGB 图像与其模糊加噪图像之间的MSE、PSNR、K 值相比，对添加高斯噪声或椒盐噪声的模糊Lena图像经过KL－RLS平滑滤波后，R－J对应的PSNR、K 值较小且MSE 大，而GK、B－L对应的PSNR、K 值较大且MSE 较小，说明影响本文算法的因素主要在于对J分量的滤波，而整幅图像的MSE、PSNR、K 值的结果均较大，说明采用KL－RLS平滑滤波算法对图像进行平滑，其过程付出了一定的细节模糊代价；③同RGB图像与直接经过KL 变换的重构图像之间的MSE、PSNR、K 值相比，RGB 图像与KL－RLS平滑滤波图像之间各性能指标的结果与②相同。

从表4可看出，无论是对模糊的Lena图像添加高斯噪声，还是添加椒盐噪声，使用自相关函数的维纳滤波的PSNR、K值均较大且MSE值较小，说明对模糊噪声图像进行滤波，自相关函数的维纳滤波算法优于常数比率维纳滤波。

对比表2、表3、表4 可以看出，与常数比率维纳滤波、自相关函数维纳滤波算法，采用KL－RLS平滑滤波算法对模糊加噪的Lena图像进行平滑滤波，其PSNR、K 值均较大且MSE值较小，说明该彩色图像平滑滤波算法优于使用常数比率维纳滤波和自相关函数维纳滤波算法。

4 结束语

本文针对彩色图像的平滑滤波问题，利用运动退化模型对Lena图像进行模糊，同时对其模糊图像添加高斯噪声和椒盐噪声，并采用常数比率维纳滤波、自相关函数维纳滤波、KL－RLS平滑滤波算法对模糊加噪的彩色图像进行滤波。仿真结果表明，与采用常数比率维纳滤波和自相关函数维纳滤波算法对彩色图像进行滤波相比较，结合KL变换和递推最小二乘法RLS对模糊加噪的RGB 图像具有良好的噪声抑制作用，可取得良好的滤波效果。从对模糊加噪的彩色图像的滤波结果来看，没有考虑彩色图像通道之间的内在联系，产生了原图像所没有的新颜色而造成图像失真。同时，经过离散KL变换的J分量来分析，其滤波效果不明显，而且与K 分量和L 分量的均方误差、峰值信噪比和相关测度值相比均较小，说明该算法还具有很大的改进和提升的空间，下一步将在这些方面进行研究改进。

［1］LI Honglin，ZHANG Qi，YANG Dawei.Improved algorithm for no－reference quality assessment of blurred image［J］.Journal of Computer Applications，2014，34 （3）：797－800 （in Chinese）.［李鸿林，张琦，杨大伟.无参考模糊图像质量评价改进算法 ［J］.计算机应用，2014，34 （3）：797－800.］

［2］LI Yueyang.Study on mehtods of color image filtering ［D］.Wuxi：Jiangnan University，2010 （in Chinese）.［李岳阳.彩色图像滤波算法的研究 ［D］.无锡：江南大学，2010.］

［3］YANG Wenbing，XU Faqiang.Color imgage smoothing based on color space transformation ［J］.Science ＆ Technology Information，2009 （35）：524－523 （in Chinese）. ［杨文兵，许法强.基于颜色空间转换的彩色图像平滑处理 ［J］.科技信息，2009 （35）：524－523.］

［4］ZHANG Chuang，CHI Jiannan，ZHANG Zhaohui，et al.Removing noise of color images based on edge detection and bilateral filter ［J］.Acta Electronica Sinica，2010，38 （8）：1776－1784 （in Chinese）.［张闯，迟健男，张朝晖，等.基于边缘检测与双边滤波的彩色图像去噪 ［J］.电子学报，2010，38 （8）：1776－1784.］

［5］LI Xuewei，ZHANG Xinrong.Automatic edge and detail preserving smoother for color image ［J］.Computer Engineering and Applications，2010，46 （3）：172－174 （in Chinese）. ［李雪威，张新荣.保持边缘和细节的彩色图像自动平滑 ［J］.计算机工程与应用，2010，46 （3）：172－174.］

［6］WANG Yan，SUN Yi.Adaptive mean shift based image smoothing and segmentation ［J］.Acta Automatica Sinica，2010，36 （12）：1637－1644 （in Chinese）.［王晏，孙怡.自适应Mean Shift算法的彩色图像平滑与分割算法 ［J］.自动化学报，2010，36 （12）：1637－1644.］

［7］DENG Tingquan，DONG Tianzhen，XIE Wei，et al.Median filtering method based on adaptive central weighting for color images［J］.Control and Decision，2013，28 （9）：1372－1376（in Chinese）.［邓廷权，董天祯，谢巍，等.自适应中心加权的彩色图像中值滤波方法 ［J］.控制与决策，2013，28 （9）：1372－1376.］

［8］MA Yide，YUAN Jinxia，ZHANG Hongjuan.Self－adaptive method using scm for noise removal in color images［J］.Journal of University of Electronic Science and Technology of China，2012，41 （5）：754－759 （in Chinese）. ［马义德，袁金霞，张红娟.自适应彩色图像SCM 去噪 ［J］.电子科技大学学报，2012，41 （5）：754－759.］

［9］CHEN Beijing，DAI Hui，LIU Quansheng.Poisson noise removal for color images using quaternion representation ［J］.Journal of Southeast University （Natural Science Edition），2013，43 （4）：717－726 （in Chinese）. ［陈北京，戴慧，刘全升.基于四元数表示的彩色图像泊松噪声 ［J］.东南大学学报（自然科学版），2013，43 （4）：717－726.］

［10］Rafael C Gonzalez.Digital image processing using MATLAB［M］.RUAN Qiuqi，transl.Beijing：Publishing House of Electronics Industry，2012 （in Chinese）.［冈萨雷斯.数字图像处理 （MATLAB版）［M］.阮秋琦，译.北京：电子工业出版社，2012.］

［11］TANG Quanwu，SHI Chongsheng，WU Jia.Potato hyperspectral image de－noising based on wavelet and recursive of least squares［J］.Journal of Gansu Agricultural University，2014 （2）：170－175 （in Chinese）.［汤全武，史崇升，吴佳.基于小波递推最小二乘滤波算法的马铃薯高光谱图像去噪［J］.甘肃农业大学学报，2014 （2）：170－175.］

［12］ZHANG Ran，TANG Quanwu，SHI Chongsheng.Recursive least squares adaptive filtering algorithm for image de－noising［J］.Computer Applications and Software，2014，31 （5）：193－196 （in Chinese）.［张然，汤全武，史崇升.基于递推最小二乘自适应滤波算法的图像去噪 ［J］.计算机应用与软件，2014，31 （5）：193－196.］

［13］CHEN Yunlong，WANG Ping，WANG Peng.Degradation image restoration algorithm based on L－R nonlinear iteration［J］.Computer Engineering，2010，36 （4）：202－204 （in Chinese）.［陈云龙，王平，王鹏.基于L－R 非线性迭代的降质图像复原算法［J］.计算机工程，2010，36 （4）：202－204.］