T样条曲面在B样条曲面局部拼接中的应用

薛 翔，周来水

（南京航空航天大学 机电学院，江苏 南京210016）

0 引 言

相邻曲面的连续拼接对于自由曲面造型［1］非常重要，因此CAD 和CAGD 领域学者对曲面拼接问题进行了大量深入的研究，例如代数曲面间拼接［2，3］、Bezier曲面间拼接［4，5］、NURBS 曲 面 间 拼 接［6，7］、以 及B 样 条 曲 面 间 拼接［8，9］。由于B样条曲面被广泛用于产品设计中的自由曲面造型，而且经常需要通过局部拼接来得到外形更灵活的B样条组合曲面，因此B 样条曲面间的局部连续拼接在产品设计时就显得更为重要。

在实际拼接时，相邻B 样条曲面在拼接边界上经常具有不同的边界定义，所以无法直接进行连续拼接。通常采用曲面细分来恢复拼接边界上的一致性，但B 样条曲面在细分时只能加入整行、整列的控制点，其中大多数控制点对曲面拼接毫无用处，只会造成拼接后曲面上的控制点冗余。相对于B样条曲面细分时控制点的成批加入，T 样条曲面［10］在细分时可以更灵活地加入局部控制点。

因此，针对B样条曲面在局部拼接时由于曲面细分而加入冗余控制点的问题，本文提出一种更有效的T样条曲面局部拼接法。该方法利用T样条曲面的局部均匀细分算法，将两张B样条曲面局部拼接为一张精简的T样条组合曲面，并通过实例验证了该拼接法优于B样条曲面细分拼接法。

1 T样条曲面基础

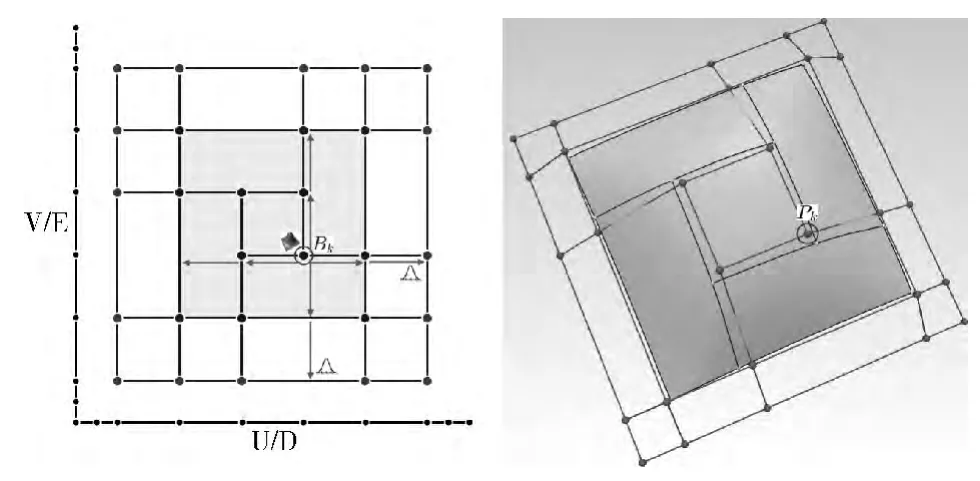
图1 T 网格及其T 样条曲面

任何一张B样条曲面都可以精确转换为一张均匀T网格上的全行列T样条曲面，如图2所示。转换后的全行列T样条曲面在曲面细分时可以加入局部控制点，而转换前的B样条曲面在曲面细分时只能加入整行、或者整列的控制点。

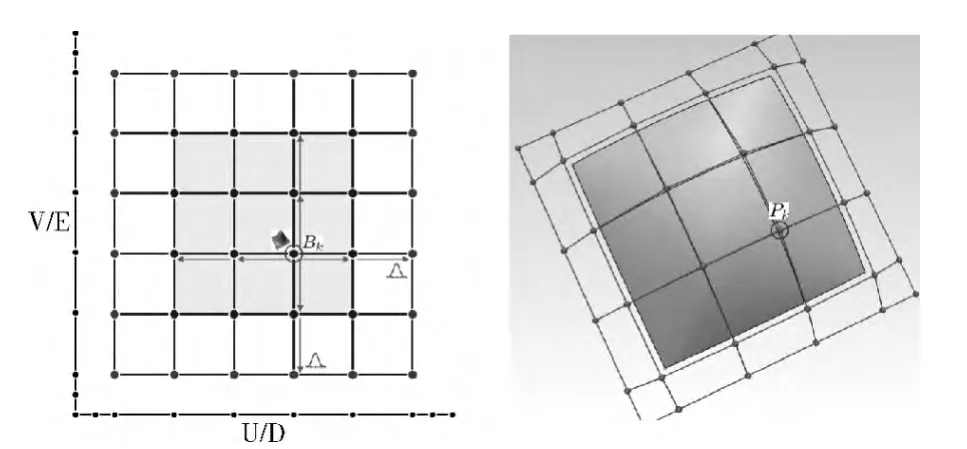
图2 均匀T 网格及其全行列T 样条曲面

2 局部均匀细分算法

T 样条曲面通过灵活的细分算法来加入局部控制点，接下来将在T 网格上具体描述其中一种较为简单的局部均匀细分算法。

给定一个T网格TMi，Bia／Bib／Bic／Bid为其上相邻4个B样条函数。如果这些B样条函数在同一方向上具有相同的支持域，就可在T网格上加入一个新控制点和一个新B样条函数Bi＋1e，如图3 所示。此时，TMi就被局部均匀细分为TMi＋1，Bia／Bib／Bic／Bid也被细分为Bi＋1a／Bi＋1b／Bi＋1c／Bi＋1d／Bi＋1e。

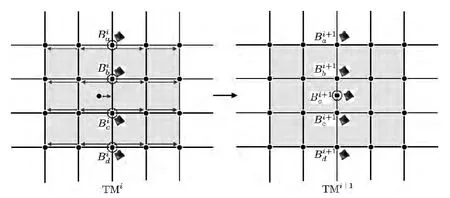
图3 T 网格上的局部均匀细分算法

利用局部均匀细分算法，就可在T 网格边界上加入局部行的控制点。如图4所示，通过对TM0进行水平方向上的局部均匀细分，可在TM0边界上加入3行局部控制点，同时将TM0局部均匀细分为TM9。

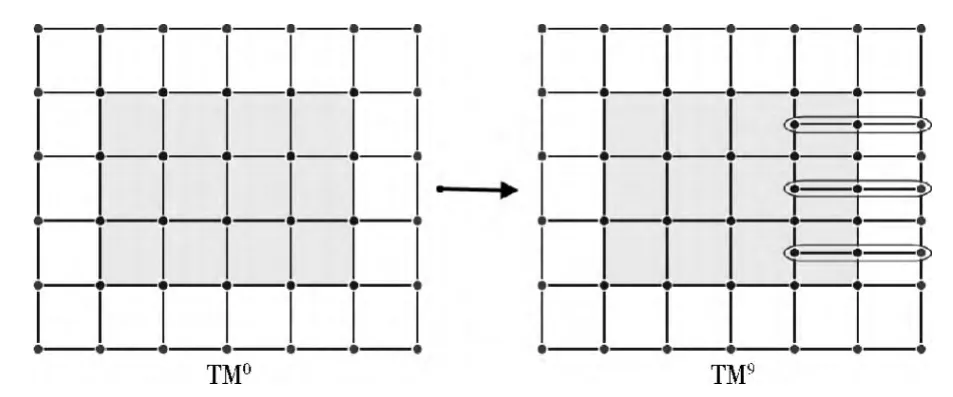
图4 T 网格边界上的局部均匀细分

3 基于T样条曲面的局部连续拼接

设两相邻B样条曲面为A 和B ，它们需要沿其公共边界Ab／Bb实现局部连续拼接，但Ab与Bb具有不同的边界定义，并且在这两张曲面的公共边界上还存在间隙与重叠，如图5 （a）所示。如果利用B 样条曲面细分来连续拼接这两张曲面，则会在拼接后的B 样条组合曲面上加入不必要的冗余控制点。如图5 （b）所示，曲面A 在局部拼接时加入了7个控制点，其中4个为冗余控制点，因为它们对曲面拼接没有任何用处。如果利用T 样条曲面的局部均匀细分算法来进行连续拼接，在曲面细分时则不加入任何冗余控制点，从而得到一张控制点更少的T 样条组合曲面。如图5 （c）所示，曲面A 在局部拼接时加入的3个控制点都不是冗余控制点，因为它们都用于曲面拼接。

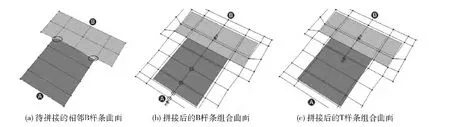
图5 相邻曲面在局部边界上的连续拼接

接下来就对基于T 样条曲面的局部拼接法进行具体描述：

步骤1 先将B样条曲面A 和B 精确转换为两张全行列T 样条曲面A 和B ，它们分别定义在均匀T 网格uTMA与uTMB上。uTMA的节点距向量为DA／EA，uTMB的节点距向量为DB／EB。拼接边界Ab与Bb也分别定义在两个边界T 网格uTMAb与uTMBb上，其各自节点距向量为DAb／EAb与DBb／EBb。由于uTMAb≠uTMBb，Ab与Bb则定义在不一致的边界T 网格上，如图6所示。因此，曲面A和B 无法直接沿其公共边界Ab／Bb实现连续拼接。

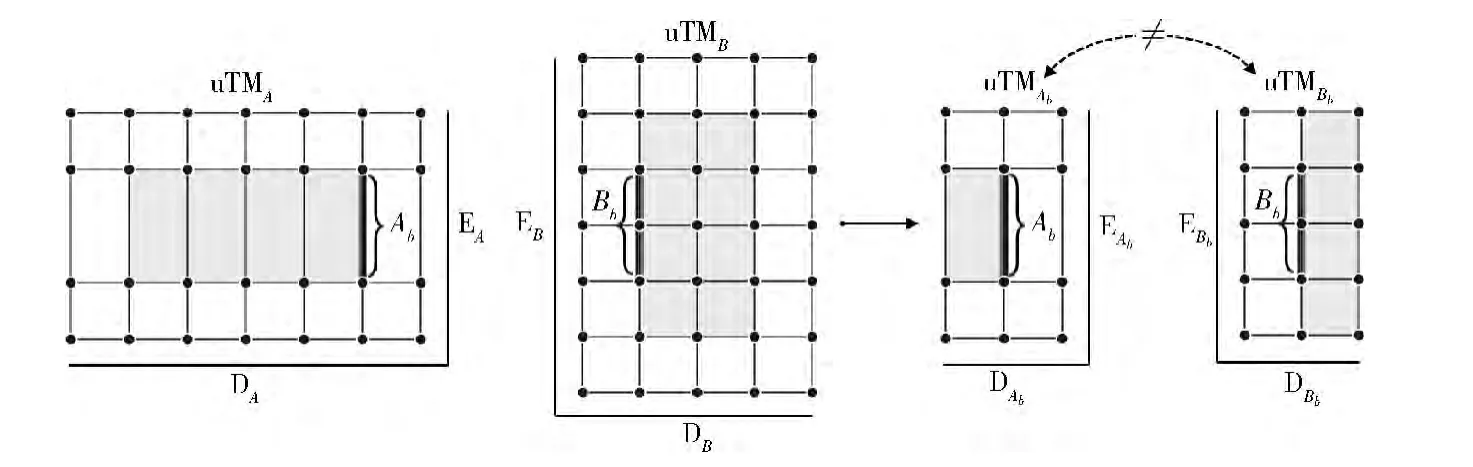
图6 拼接前不一致的边界T 网格

步骤2 通过局部均匀细分算法在T 网格边界上加入局部控制点，不仅可使Ab与Bb重新定义在一致的边界T网格上，而且还不加入任何冗余控制点。如图7 所示，通过在uTMA边界上加入一局部行的控制点，将uTMA局部均匀细分为TMA，就可使Ab与Bb的边界T 网格重新恢复一致，也即uTM′Ab＝uTMBb，其中DAb＝DBb和E′Ab＝EBb。此时只要重合Ab与Bb的控制点，就可将曲面A 和B沿其局部边界连续拼接为一张精简的T 样条组合曲面，如图5 （c）所示。

4 造型实例

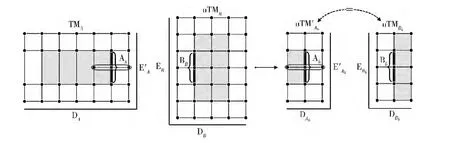
图7 局部均匀细分后一致的边界T 网格

本文在VC＋＋与VTK 渲染库的基础上实现了基于局部均匀细分的T 样条曲面局部拼接法，并将其用于车尾部的后围板曲面造型。图8 （a）为待拼接的3张相邻B 样条曲面A／B／C。由于曲面A 与曲面B 和C 在各自拼接边界上具有不同的边界定义，因此这3张曲面无法直接实现局部连续拼接。为得到图8 （b）中连续拼接后的组合曲面，接下来将利用B样条曲面细分拼接法与T 样条曲面局部拼接法分别构建后围板的曲面模型。

在图9 （a）中，B样条曲面A 通过曲面细分使其与曲面B 和C 在拼接边界上具有一致的边界条件，从而实现曲面间的连续拼接。但B样条曲面A 在细分时必须加入两整行的控制点，总共为40个控制点，其中28 个控制点对曲面拼接没有任何用处。拼接后的后围板曲面模型将由一张B样条组合曲面来描述。

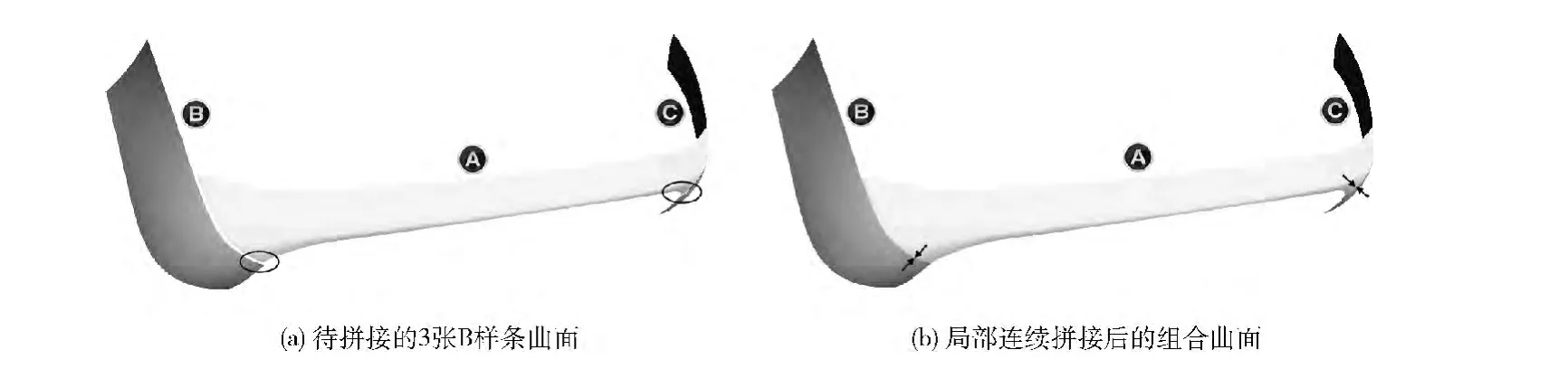
图8 后围板曲面模型的构建

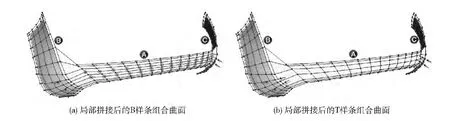
图9 基于曲面细分的后围板曲面拼接

如果将这3张B 样条曲面转换为全行列T 样条曲面，就可利用局部均匀细分来得到拼接边界上的一致性，从而将这些曲面局部连续拼接在一起，如图9 （b）所示。此时只需在全行列T 样条曲面A 的两侧分别加入两行局部控制点，一共为12个控制点，这些控制点全部用于曲面拼接，并且只有图9 （a）中B样条曲面细分拼接时所加控制点的30%。此时，后围板曲面模型就可由一张更精简的T 样条组合曲面来描述，其上的控制点更少。

5 结束语

本文提出的T 样条曲面局部拼接法较好地解决了相邻B样条曲面在局部拼接时由于曲面细分而加入冗余控制点的问题。该拼接法利用T 样条曲面的局部均匀细分来实现拼接边界上的一致性，同时不加入任何冗余控制点，因此在局部拼接后可以得到一张更精简的组合曲面。最后，通过实例验证了该拼接法比B 样条曲面细分拼接法更有效，并且还具有较好的工程应用价值。

［1］SHEN Junhua，SHI Guizhen.Review on the free curves and surfaces modeling theories ［J］.Information Technology，2013，37 （3）：184－187 （in Chinese）. ［沈俊华，史贵振.自由曲线曲面造型理论发展综述 ［J］.信息技术，2013，37（3）：184－187.］

［2］LI Yundong，ZHANG Xianjun.Blending of two algebraic surfaces by PDE method ［J］.Journal of DALI University （Natural Science），2010，9 （4）：23－25 （in Chinese）.［李云东，张先君.应用PDE方法构造两个代数曲面拼接 ［J］.大理学院学报 （自然科学版），2010，9 （4）：23－25.］

［3］LI Yundong，LUO Jing.Smooth blending of two algebraic surface along planar sections［J］.Journal of Chengdu University of Information Technology，2008，23 （3）：333－336 （in Chinese）.［李云东，罗静.两个代数曲面沿平面截口的光滑拼接［J］.成都信息工程学院学报，2008，23 （3）：333－336.］

［4］LIU Huili，MENG Qingxian.Smooth connection of triangular Bézier patches with a common vertex ［J］.Journal of Compu－ter－Aided Design ＆Computer Graphics，2009，21 （8）：1074－1082 （in Chinese）.［刘会立，孟庆贤.绕一角点的Bézier三角曲面片的光滑拼接 ［J］.计算机辅助设计与图形学学报，2009，21 （8）：1074－1082.］

［5］HU Gang，ZHANG Nianjuan，QIN Xinqiang，et al.Research on the smooth splice for cubic Bézier curves and surfaces with multiple shape parameters［J］.Journal of Xi’an University of Technology，2009，25 （4）：482－486 （in Chinese）.［胡钢，张念娟，秦新强，等.带多形状参数的三次Bézier曲线曲面的光 滑 拼 接 ［J］.西 安 理 工 大 学 学 报，2009，25 （4）：482－486.］

［6］YANG Huogen，WU Wendi.A method of G1smooth connection between adjacent NURBS surfaces［J］.Journal of Nanchang University（Natural Science），2010，32 （2）：124－126 （in Chinese）.［杨火根，吴问娣.一类邻接NURBS 曲面G1 光滑拼接方法［J］.南昌大学学报（理科版），2010，32 （2）：124－126.］

［7］WU Lushen，GAO Xiangqing，XIONG Hui，et al.Improved curve surface seamless splicing based on NURBS ［J］.Optics and Precision Engineering，2013，21 （2）：431－436 （in Chinese）.［吴禄慎，高项清，熊辉，等.改进的NURBS曲面片拼接算法 ［J］.光学精密工程，2013，21 （2）：431－436.］

［8］ZHAO Nailiang，REN Xin，MA Weiyin.Properties and applications of connecting functions for GC1－connected B－spline surfaces［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2009，21 （8）：1061－1065 （in Chinese）.［赵乃良，任歆，马维银.B样条曲面GC1拼接中连接函数性质及其应用［J］.计 算 机 辅 助 设 计 与 图 形 学 学 报，2009，21 （8）：1061－1065.］

［9］JIN Xijuan，YAO Jie，FANG Kui.Convexity preserving connection for B－spline surfaces［J］.Microcomputer ＆Its Applications，2011，30 （23）：51－53 （in Chinese）. ［金席卷，姚杰，方逵.B－样条曲面的保凸拼接 ［J］.微型机与应用，2011，30 （23）：51－53.］

［10］LI Xin.T－splines and splines over T－meshes ［D］.Hefei：University of Science and Technology of China，2008：1－130（in Chinese）. ［李新.T 样条和T 网格上的样条 ［D］.合肥：中国科学技术大学，2008：1－130.］