基于有向滑动时间窗的报警动态选择算法
汪永伟,苏会芳,张红旗,刘育楠,邱 卫
(1.信息工程大学,河南 郑州450004;2.河南省信息安全重点实验室,河南 郑州450004;3.河南省外贸学校,河南 郑州450002)
0 引 言
报警关联分析可以在相关的报警信息之间建立关联,消除冗余报警,能够有效降低系统中的报警数量,提高网络安全状态分析的效率和准确性[1-3]。新报警来临时,需要从已有报警中选择一个或一组报警与之建立关联。在现有关联分析方法中,报警选择主要采用两种方法:第一种方法是,选择所有的已有报警与新报警建立关联[4-6];另外一种方法是,将最近的关联报警划分为若干时间窗,从时间窗中随机选择报警与新报警建立关联[7]。第一种方法实现较为简单,关联结果最为精确,但是计算资源消耗巨大,关联方法的实时性受到影响,不适于实时在线态势分析[8];相对于第一种方法,第二种方法在性能上有所提升,但是由于报警选择的无目的性,一定程度上会降低关联分析的准确性。
针对上述问题,本文提出了一种基于有向滑动时间窗的报警动态选择算法ADSA_DSTW (alert dynamic selection algorithm based on direct slide time window)。该算法依据历史关联结果的趋向特征,调整每个时间窗内报警抽取的概率,向历史关联强度高的时间窗分配更高的抽取概率,以提高报警关联的实时性和准确性。
1 基于有向滑动时间窗的报警动态选择算法
1.1 基本思想
新报警来临时,报警选择策略决定了已关联报警的抽取原则。报警全选方法虽然精准,但是资源消耗巨大;随机选择方法虽然性能优异,但是精确度下降。在采用报警随机选择方法时,按照时间窗的新鲜度,从每个时间窗内随机抽取报警建立关联对,在整个关联过程中,某一时间窗所获得的抽取概率始终完全相同[7]。随机选择方法考虑了窗口新鲜度因素,相对比较合理,但是,其没有考虑关联历史因素。在关联过程中,时间窗内的历史关联强度会对新的报警关联带来有益的启示:由于关联报警在时间上具有聚集性,历史关联强度更高的时间窗与新报警发生关联的概率更大,历史关联强度低的时间窗与新报警关联的可能性较小。这一特征与计算机网络中的拥塞管理机制类似:在经典的网络管理中,当丢包状况提示网络发生拥塞时,拥塞控制算法会降低窗口大小,减少数据包发送规模;当网络状态良好时,增加窗口大小,拥塞控制算法扩大数据包发送规模。
因此,受经典计算机网络中拥塞窗口管理机制的启发,本文提出了一种基于有向滑动时间窗的报警动态选择算法ADSA_DSTW。ADSA_DSTW 算法依据历史关联结果的趋向特征,调整每个时间窗内报警抽取的概率,向历史关联强度高的时间窗分配更高的抽取概率,降低历史关联强度较低的时间窗的抽取概率,从而提高报警关联的效率和准确性。
1.2 初始报警选择
假设,将时间划分为n个等间隔的时间窗,每个时间窗的序号从1到n。按照报警产生的顺序,将每个报警分配到对应的时间窗内,其所隶属的时间窗序号通过式 (1)获得
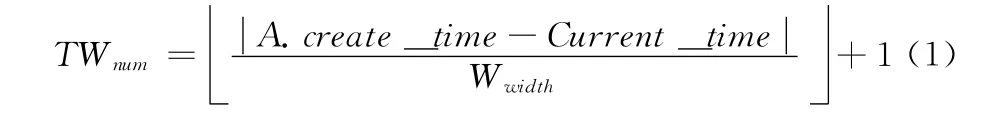
发生越久的报警与新报警发生关联的概率越小,因此,在报警选择上,可为其分配较低的抽取概率。
假设,序号为i的时间窗内的报警数量为si,窗口报警抽取概率为ρ,报警选择数位select_numi,则,在初始状态下,时间窗的抽取概率和从其中可选择的报警数量为

由式 (1)可以看出,报警产生越久,其所属时间窗的序号越大,根据式 (2)计算的抽取概率越小,进而由式(3)所分配的告警选择数越小。
例如,图1所示的时间窗中,时间窗的序号由左到右依次为。依据式 (2)、式 (3),从每个窗口中选择的报警数量分别为3,5,9,8和12。每个窗口对应的抽取概率分别为18.7%,35.7%,60%,72.7%,100%,越新鲜的时间窗被分配的抽取概率越大。

图1 初始报警选择
1.3 ADSA_DSTW 报警动态选择算法
假设,Comax表示新报警Anew与时间窗Ti内已有报警关联过程中关联强度的最大值。Seaverage是历史上的报警关联强度均值。时间窗的报警抽取概率通过调节报警选择数量来实现,调整过程中的两个阈值分别为:最小报警选择调整阈值SeThreshmin和最大报警选择调整阈值SeThreshmax

其中,α为调节参数,用于调节报警选择数量的变化速度,取值范围 [0.5,1.0]。α值较大时,时间窗内报警选择数量的调整速率较快;α值较小时,时间窗内报警选择数量的调整速率较慢。为了保证报警选择调节的有效性,α的选择需保证SeThreshmax<CoT 。
由前面的分析可知,历史关联强度更高的时间窗与新报警发生关联的概率更大,历史关联强度低的时间窗与新报警关联的可能性较小。本文将新报警与时间窗内报警关联的可能性定义为关联兴趣度CI(correlation interest)。
定义1 关联兴趣度由本次报警关联过程中的最大值Comax与SeThreshmax、SeThreshmin之间的关系决定,其计算方法如下
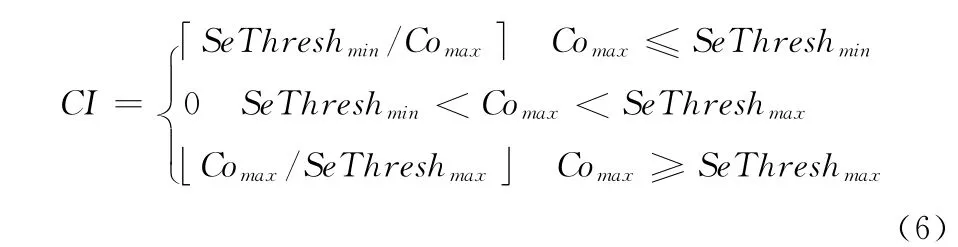
ADSA_DSTW 算法的工作原理为:
首先,利用式 (2)和式 (4)计算每个时间窗的初始select_numi。然后,在新报警Anew与时间窗Ti内报警的关联过程中,不断更新最大关联强度Comax。当时间窗Ti内检测过的报警数量超过select_numi/2时,检验Comax与调整阈值之间的关系。若Comax小于SeThreshmin,说明Anew与时间窗Ti内报警发生关联的兴趣度较小,则减小该时间窗的报警选择数量,将select_numi减小CI;若Comax大于SeThreshmax,说明Anew与时间窗Ti内报警发生关联的兴趣度较大,则增大该时间窗的报警选择数量,将select_numi增加CI。
算法1给出了基于有向滑动时间窗的报警动态选择算法的伪码描述。

算法1基于有向滑动时间窗的报警动态选择算法ADSA_DSTW输入:Alertnew,Rules输出:SelectedAlerts(1) BEGIN(2) n=SetTWcount();(3) For i=1:n(4) selectNum [i]=si*(1-i-1)n(5) j=0;//(6) Comax =-1;(7) While(j<selectNum [i])&& (j<si)(8) a=randSelect();(9) Ctemp=caculateCorrelation (Alertnew,a);(10) If(Ctemp>Comax )(11) Comax =Ctemp;(12) End if(13) j=j+1;(14) If (j > selectNum[i]2 ) && (Comax<SeThreshmin )(15) selectNum [i] =selectNum [i]-SeThreshmin/Co max ;(16) End if(17) If(j==selectNum [i])&& (Comax >SeThreshmax )&& (j<si)(18) selectNum [i] =selectNum [i] +Comax/SeThresh max ;(19) Comax =0;(20) End if(21) End while(22) End for(23) End
其中,第 (2)-(6)行完成初始参数和初始报警选择数量设置。第 (8)-(12)行记录报警关联过程中的最大关联强度。第 (14)-(20)依据历史报警关联强度对报警选择数量进行动态调整。
通过ADSA_DSTW 的动态调整策略,历史关联强度较高的时间窗所分配的select_numi逐渐变大,相应的报警抽取概率会逐渐提高。在时间窗内报警数量较多的情况下,历史关联强度高、关联趋向特征明显的时间窗所分配的报警选择数增加的也更快,而历史关联强度低、不相关趋向特征明显的时间窗所分配的报警选择数的下降则会迅速下降,从而使报警的选择过程更具目的性,提高报警关联的效率和准确性。
2 实验仿真与分析
2.1 实验方法
为了验证本文提出的报警选择算法对关联分析性能的作用,本文在文献 [9]所提出的关联分析方法的基础上加载了ADSA_DSTW 算法,在LLDOS1.0数据集上分别测试了报警全选、随机选择和本文的ADSA_DSTW 对报警关联执行时间的影响。实验数据共分为8组,每组实验输入的报警数分别为120、225、350、450、600、700、800、900,时间窗个数n=10。为了测试时间窗大小对执行时间的影响,分别测试了8组报警数据在时间窗大小Wwidth=100s、Wwidth=200s和Wwidth=300s的运行结果。
在实验中,为了测试报警选择算法对关联精度的影响,在测试结果对比分析过程中,采用文献 [10]提出的关联分析结果评价指标:完备率CR (completeness rate)和有效率SR (soundness rate)。
定义2 完备率[10]:该指标用于评价关联方法的对关联报警的发掘能力,是正确关联的报警数与实际相关报警数的比率,计算方法如式 (7)所示

定义3 有效率[10]:该指标用于评价关联方法的正确性,是正确关联的报警数与已建关联总数的比率,计算方法如式 (8)所示

2.2 实验结果
图2给出了不同报警选择方法在Wwidth=100s情况下的运行时间对比。图3给出了报警动态选择算法在Wwidth=100s、Wwidth=200s和Wwidth=300s情况下的运行时间对比。图4给出了报警动态选择算法在不同时间窗下的精度对比。
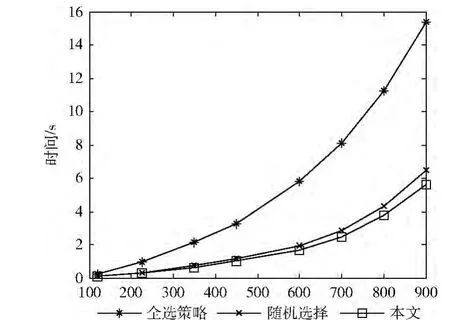
图2 报警选择实验结果 (窗口100s)
2.3 实验分析

图3 时间窗大小对运行时间的影响

图4 时间窗大小对关联精度的影响
由图2可以看出,报警全选方法的执行时间几乎呈指数曲线变化,而随机选择算法和ADSA_DSTW 算法的执行时间明显要低于报警全选的执行时间。当输入报警的数量较少时,随机选择算法和ADSA_DSTW 算法的执行时间差别不大,随着报警集中报警数量的增加,两者在执行时间上的差异逐渐扩大,当报警数量达到900时,ADSA_DSTW 算法的测试组在执行时间上比随机选择算法的测试组降低了13.93%,比全选测试组降低了63.41%。这是因为,当时间窗内报警数量较多时,ADSA_DSTW 算法能够基于历史关联概率对窗口内的报警选择次数进行调整,将抽取概率快速倾斜向于历史关联强度高的时间窗,减少了新报警与无关窗口中报警的关联运算次数,从而降低了整体报警关联执行过程的运行时间。
图3是不同时间窗大小情况下的运行时间对比。可以看出,时间窗的大小对报警关联的执行时间有一定影响,时间窗变大时,运行时间相应变长。这是因为,窗口变大时,每个窗口中的报警数量增加,初始报警选择数量分配时的基数变大,相应的,通过报警选择算法从每个时间窗内平均选择的报警数量增多,可以想象,当报警窗口扩大到整个历史区间时,初始的报警选择数就是所有报警的数量,因此,窗口的扩大会导致整个关联执行时间的增加。
图4是不同时间窗大小情况下的有效率和完备率对比。可以看出,时间窗的大小对报警关联的精度有一定影响,时间窗减小时,关联完备率相应降低。这是因为,窗口减小时,每个窗口中的报警数量减少,初始报警选择数量分配时的基数变小,相应的,通过报警选择算法从每个时间窗内平均选择的报警数量减少,报警选择数量的减少必然会漏掉可能的报警关联对。因此,窗口的减小会导致关联完备率的下降。因此,在实际运行过程中,通过调节窗口大小,可适应对不同实时性和精度要求的应用场景。对于一些对实时性要求较高的关联分析场景,可以选择相对较小的时间窗,以提高关联效率;而对精度要求较高的关联分析场景,则可以选择较大的时间窗,以提高关联精度。
3 结束语
针对现有报警选择方法在实时性和精确性方面存在的不足,本文提出了一种基于有向滑动时间窗的报警动态选择算法。该算法依据历史关联结果的趋向特征,调整每个时间窗内报警抽取的概率,向历史关联强度高的时间窗分配更高的抽取概率,降低历史关联强度较低的时间窗的抽取概率,从而提高报警关联的效率和准确性。仿真结果表明,ADSA_DSTW 算法的运行时间随着时间窗的减小而减小,在运行时间上远低于报警全选方法和随机选择方法;ADSA_DSTW 算法的完备率受时间窗大小的影响较大,随着窗口的增大而增大,而有效率则保持相对稳定。通过窗口大小调节,ADSA_DSTW 算法与报警关联分析方法相结合可适应对不同实时性和精度要求的应用场景。
[1]Peng L,Chen W,Xie D,et al.Dynamically real-time anomaly detection algorithm with immune negative selection [J].Appl Math,2013,7 (3):1157-1163.
[2]Chen S.Optimized multilevel immune learning algorithm in abnormal detection [J].Information Technology Journal,2013,12 (3):514-517.
[3]Suarez-Tangil G,Palomar E,Pastrana S,et al.Artificial immunity-based correlation system [C]//SECRYPT,2011:422-425.
[4]LIU J,LI Y,MENG J,et al.Intrusion detection system alerts fusion based on fuzzy comprehensive evaluation and immune evolution [J].Journal of Computational Information Systems,2013,9 (4):1509-1516.
[5]Kabiri P,Ghorbani A.A rule-based temporal alert correlation system [J].International Journal of Network Security,2007,5 (1):66-72.
[6]Ren H,Stakhanova N,Ghorbani A.An online adaptive approach to alert correlation [M].Detection of Intrusions and Malware,and Vulnerability Assessment,Springer Berlin Heidelberg,2010:153-172.
[7]Ahmadinejad H,Jalili S.Alert correlation using correlation probability estimation and time windows[C]//Proceedings of the International Conference on Computer Technology and Development,IEEE,2009:170-175.
[8]Bateni M,Baraani A.Time window management for alert correlation using context information and classification [J].International Journal of Computer Network &Information Security,2013,5 (11):9-16.
[9]Bateni M,Baraani A,Ghorbani A A.Using artificial immune system and fuzzy logic for alert correlation [J].Int J Netw Secur,2013,15 (1):160-174..
[10]Elshoush H T,Osman I M.Alert correlation in collaborative intelligent intrusion detection systems-a survey [J].Applied Soft Computing,2011,11 (7):4349-4365.

