可逆乘除法指令的设计与仿真

朱鹏程，管致锦

（1.南通大学 杏林学院 计算机科学与技术系，江苏 南通226019；2.南通大学 计算机科学与技术学院，江苏 南通226019）

0 引 言

可逆计算在计算过程中不丢失信息，因此可从根本上避免由于信息丢失而导致的热耗散，目前对可逆计算的研究主要集中在低功耗CMOS电路［1］、量子电路［2］的逻辑综合方面，对可逆编程语言［3］和可逆指令系统［4－6］也有所涉及。

指令系统处于软件层和硬件层之间，其设计是否逻辑可逆对整个系统能否物理可逆至关重要。PISA （Pendulum instruction set architecture）［4］是运行在可逆处理器Pendulum 的可逆指令系统，其设计遵循RISC 规范，包含各类使用频度较高的简单指令。Axelsen 对PISA 作了形式化描述［4］，对个别指令的实现细节作了调整 （如RBRA 指令），并验证了PISA 中无论是算术／逻辑运算指令，还是各种跳转指令，都是对系统状态的可逆更新。由于可逆乘法器和除法器的设计较为复杂，可逆处理器Pendulum 的ALU 中未包含乘法和除法部件，因此PISA 指令集中也未包含乘法、除法指令。Bob是一种基于哈佛体系结构［5］的可逆处理器，其指令系统BobISA［6］定义了一种用于整数的可逆乘法指令和除法指令，但这两个指令只能进行乘2或除2操作，且除2操作只有当被除数是偶数时能返回相应结果。这种乘除法指令所受局限性较大，不能进行任意整数间的乘除操作，因此不具备通用性。

本文拟为PISA 指令系统扩展可逆乘法和除法指令。指令扩展通常有两种常用方式：一是通过硬件实现，二是通过指令串或子程序模拟。本文采用第二种方式，基于PISA指令系统中的原有指令，根据可逆编程原则，构建乘除法的可逆子程序段。最终得到的乘法除法指令应满足以下条件：①乘法指令和除法指令在格式上保持一致，即在操作数的个数以及操作数的意义保持对称；②组成乘法或除法的子程序必须逻辑可逆，即无论正向运行还是反向运行都应具备确定性；③乘法指令和除法指令互为逆指令，即乘法的正向运行效果等价于除法反向运行，反之亦然。鉴于计算机中的运算可以由硬件实现，也可以由软件实现，但其在逻辑上存在共通之处，因此本文采用的子程序扩展指令的方式，对如何设计硬件乘法器和除法器有一定指导意义。

1 PISA指令系统以及可逆编程原则

现代计算机的指令系统在设计时均没有考虑逻辑可逆性，因此绝大多数指令都是逻辑不可逆，PISA 对这些指令通过增加操作数的方式进行扩展，确保其中每一条指令均可逆。另外，使用机器语言或汇编语言编程原本就比使用高级语言要复杂很多，再加上逻辑可逆的约束，工作将更为复杂，因此有必要参照结构化程序设计的方式，对可逆汇指令串中的分支结构、循环结构以及方法调用等在形式上作一些规范。

1.1 相关概念

首先介绍文章中涉及的几个概念。

概念1：逆指令。指令i和指令inv（i）互为逆指令当且仅当满足以下条件

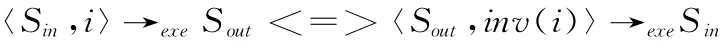
式中：Sin和Sout——指令执行前后的系统状态 （由各寄存器、存储器状态构成），→exe——指令执行。

概念2：可逆更新。给定函数f：D →B 和运算符⊙：（A×B）→C，其中运算符⊙对其第一参数A 单射，存在函数g（A×D）→（C×D）使得g（x，y）＝（x⊙f（y），y）是对其第一参数x 的可逆更新，且其逆更新为：g－1（x，y）＝（x⊕f（y），y），其中⊙和⊕互为逆运算符 （比如加法运算符与减法运算符）。

1.2 PISA指令系统

PISA 是一个完备的指令系统，含近40 条指令，其中包括算术／逻辑运算指令、程序控制指令以及数据传输指令等。表1中给出部分PISA 指令，其中指令栏显示PISA 指令，逆指令栏显示语义与其相反的逆指令，语义栏显示该指令执行的效果，其它未在表中展示的指令可查阅文献［4］。表1中R1、R2、R3表示寄存器，IMM 表示立即数，ROL表示循环左移操作，⊕表示异或运算，∧表示与运算，∨表示或运算，＜＜表示逻辑左移操作，OFF 表示跳转偏移量，DIR 表示程序运行方向 （正向时取1，反向时取－1），BR 表示跳转寄存器，表示交换。

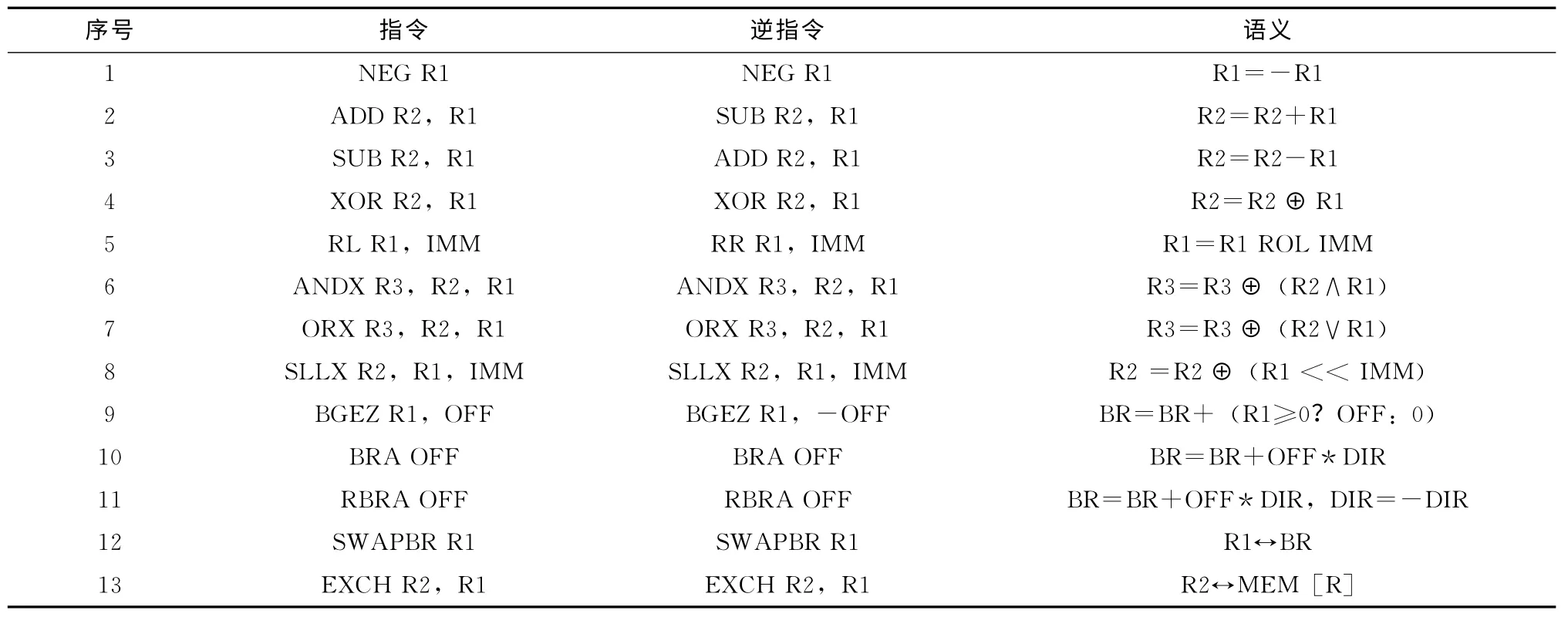
表1 PISA 指令集

现流行指令系统如8086等，虽然设计时没有考虑逻辑可逆性，但确实包含一部分指令是可逆的，这部分指令可以不作变动直接纳入可逆指令集，比如表1中指令1－5。这几条指令逻辑可逆的根本原因在于，无论是加法运算、减法运算还是异或运算都是对其第一参数的单射变换，这样的运算必然存在逆运算，因此其对系统状态的更新属于可逆更新［7］。比如 “ADD R2，R1”指令，其将寄存器R2和R1的值相加并将结果保存在R2中，反向执行时，将该指令替换为其逆指令即 “SUB R2，R1”，逆指令执行结束后，R1和R2回复初始状态。

此外，现有指令系统中大部分指令是逻辑不可逆的，比如8086中的 “AND R2，R1”，其将寄存器R1和R2的内容相与并将结果保存到R2中去，但由于与运算的运算规则，反向运行时无法根据R1和R2的当前状态回复到初始状态，所以该指令逻辑不可逆。PISA 中通过扩展指令的方式使相应指令实现逻辑可逆，比如 “ANDX R3，R2，R1”，其将R1和R2相与的结果与R3进行异或，并将最终结果保存在R3中，R1和R2的内容在指令执行过程保持不变，当R3初值为0时，该指令执行后R3中保存的内容便是R1与R2 进行与运算的结果。由于异或是一种可逆运算，ANDX的逆指令便是本身。表1中的指令6～8均是通过类似扩展从而实现逻辑可逆的。

为使程序可逆，仅算术运算、逻辑运算指令可逆还不够，只有当控制逻辑同时可逆时程序才能真正具备反向确定性。8086等类似指令系统中的转移指令是不可逆，如图1 （a）所示，反向运行到JTO 处时存在二义性，无法判断是该逐条执行还是跳转。PISA 通过转移指令对的形式实现控制结构的可逆，如图1 （b）所示，PISA 要求转移指令的目的地必须同样是转移指令，且该目的指令指向源转移指令。表1所示指令9是无条件移指令，PISA 中还包含其它条件转移指令如BEQ、BGEZ 等。指令11 和12 是特殊指令，其中RBRA 指令主要用于反向子过程调用，SWAPBR指令主要作为子过程的入口和出口。

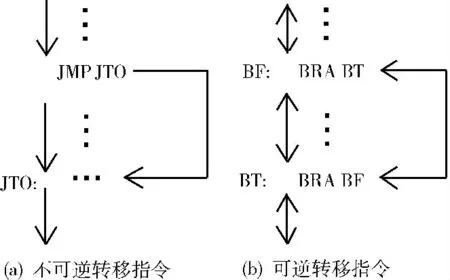
图1 转移指令的结构

为确保控制逻辑可逆，PISA 中的转移指令不直接修改PC寄存器，仅修改BR 寄存器 （该寄存器用于保存跳转偏移量），然后由控制器根据执行方向DIR 和BR 寄存器的内容对PC寄存器进行可逆更新，更新逻辑如下

表1中的指令13是PISA 中用于访问内存的指令，该指令通过交换寄存器和指定内存单元的内容实现内存访问，显然该指令的逆指令就是其自身。

1.3 可逆编程原则

使用PISA 指令集进行编程，应该注意以下几点：

（1）“ANDX R3，R2，R1”等扩展指令在程序中原则上应成对出现，如表2 所示。第一次使用该指令将R1 和R2相与的结果保存在R3中，第二次使用则借助R1和R2相与的结果清空R3。为能正确清空R3，两次使用期间R3、R2以及R1寄存器的值均不能被改变。可以发现，经过两次执行ANDX 指令，相关寄存器的状态回复为指令执行前的初态，这表明ANDX 指令是可逆的，且其逆指令为自身。在两次使用类似扩展指令期间，应尽量避免相关寄存器内容发生改变，否则会破坏逻辑可逆性。

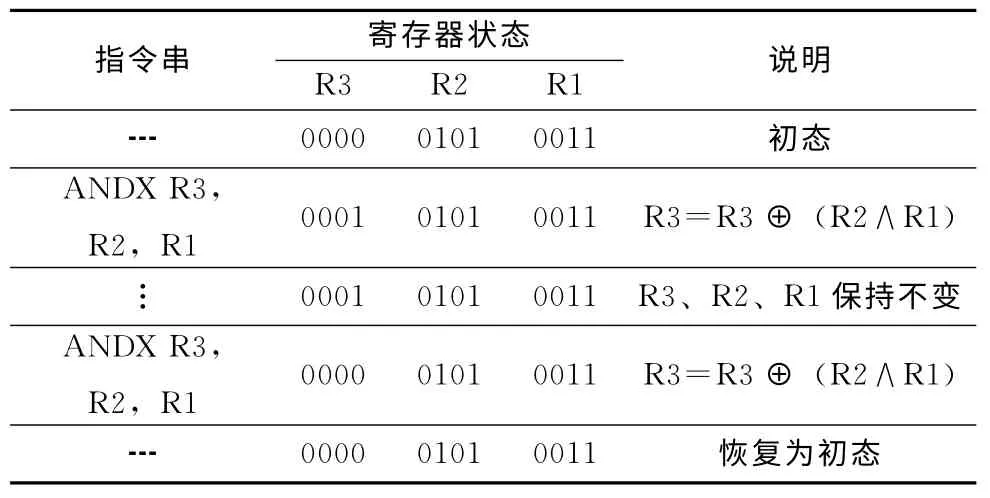
表2 扩展指令的使用原则 （数字形式以二进制表示）

（2）通过指令对的形式保持程序控制结构可逆，即某转移指令的目的指令必须是指向其自身的转移指令 （如图1所示），或是SWAPBR 指令。前者主要用于控制分支结构或循环结构，后者主要用于子过程调用或反向子过程调用。

（3）另外采用形如结构化程序设计的 “单入口单出口”控制结构，以简化编程难度，防止出现面条式代码。PISA中采用的分支结构以及循环结构如图2所示。

图2 可逆分支结构和循环结构

图2中竖直箭头表示顺序执行，折线箭头表示跳转执行，虚线表示反向执行。区别于经典分支结构，可逆分支结构和循环结构在入口和出口处均要作条件判断以确保反向确定性。在简单分支结构中，为降低编程难度可以使前置条件和后置条件保持相同，前提是分支执行过程中条件判断涉及的寄存器状态不能被改变。循环结构中的前置条件和后置条件一般不同，在初次进入循环时前置条件一般不满足，否则直接跳过循环结构，当循环若干次后，后置条件不满足时退出循环。更详细的说明或更复杂的控制结构请查阅文献 ［4］。

（4）子过程结构及其正向和反向调用如图3 所示，BRA、RBRA 等指令含义如表1所示。与经典子过程不同的是，可逆子过程调用时的入口和返回时的出口相同，即图3中的SWAPBR 指令处。对于同一子过程 （如二进制转换十进制子过程BinToDec），正向调用 “BRA BinToDec”表示按如图3 （a）所示箭头方向执行子过程，并用原语义解释所遇的每条指令，最终实现二进制向十进制的转换；反向调用 “RBRA BinToDec”则表示按如图3 （b）所示箭头方向反向执行子过程，并以相应逆指令语义解释所遇的每条指令，最终实现十进制向二进制的转换。这种子过程实现和调用方式，使得二进制与十进制间相互转换能共享同一子过程。本文中的乘法和除法子过程均是采用这种结构，因此两个子过程均支持正向调用和反向调用。关于子过程调用更详细的解释可以查阅文献 ［4］。

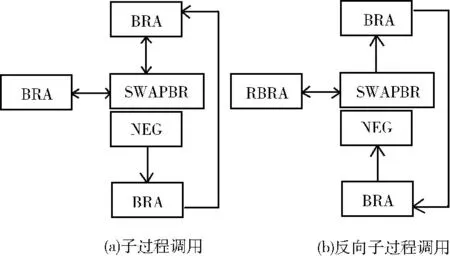
图3 可逆子过程

2 可逆乘法指令和除法指令

为清晰的说明设计思路并降低实现难度，以下乘法运算和除法运算均针对无符号正整数，其中乘法运算限于4位×4位，除法运算限于8位÷4位。

2.1 设计约束

拟基于现有PISA 指令集，通过子过程的方式扩展乘法和除法指令，扩展的乘除法指令能像加减法指令一样，互为逆指令。因为可逆子过程既支持正向运行，又支持反向运行，所以由此扩展的指令同样具备双向运行的特性。

2.1.1 乘除法指令格式

逻辑可逆要求在运算过程不能丢失信息，因此若要正整数除法指令可逆，则应保留足够的信息。除法运算涉及4个操作数，分别是被除数、除数、商以及余数，但结果只要保留除数、商以及余数便可实现逻辑可逆，因此如图4所示可逆除法指令需要3个操作数，其中操作数1在指令执行前表示被除数，在执行后表示余数。

虽然正整数乘法指令一般只需要保存两个操作数 （如积和乘数）就能逻辑可逆，但为了实现乘除法指令互为逆指令的目的，也将采用3操作数以在指令格式上与除法指令对称，如图4所示，操作数1 初值可以不为零，对应除法指令的余数，乘法指令执行后操作数1的值等于被乘数与乘数的积和其初值之和，对应除法指令中的被除数，图4中的箭头表示乘法指令和除法指令各操作数之间的对称关系。

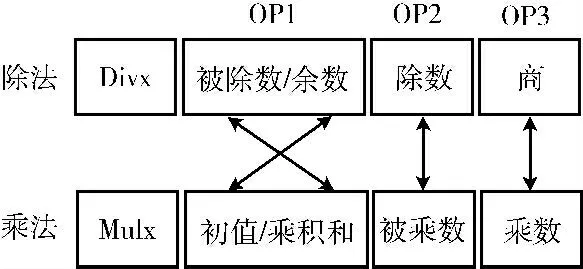
图4 乘除法指令格式及其操作数对应关系

2.1.2 参数传递方式

图4仅是乘法指令和除法指令的逻辑结构，其实际功能将通过如图3所示的子过程实现。调用子过程时需传递参数，拟采用寄存器参数传递法实现传参，即在主程序中将操作数存入事先约定的寄存器中，进入子程序后再取出进行处理。拟将操作数OP1、OP2以及OP3分别存放在寄存器R3、R2以及R1中。

2.1.3 子过程调用形式以及执行模式

将乘法子过程命名为Multx，除法子过程命名为Divx。由于可逆处理机Pendulum 在程序运行过程中可以通过翻转DIR 的取值随时切换运行方向，因此被调用的子过程是正向执行还是反向执行由调用时的跳转指令和处理器DIR 当前值共同决定，见表3。

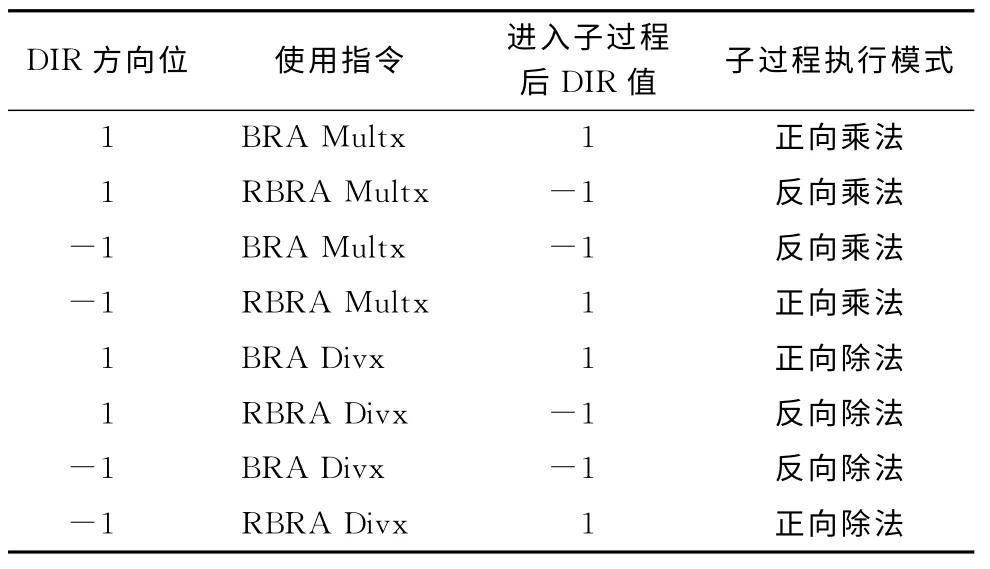
表3 子过程执行模式

在处理机的DIR 方向位预设为1时 （即平台处于正向运行模式），通过 “BRA Multx”指令跳转到乘法子过程并正向执行；通过 “RBRA Multx”指令跳转到乘法子过程，翻转方向位DIR，并反向执行。当处理机的DIR 方向位预设为－1时 （即平台处于反向运行模式），通过 “BRA Multx”指令跳转到乘法子过程并反向执行；通过 “RBRA Multx”指令跳转到乘法子过程，翻转方向位DIR，并正向执行。即乘法子过程Multx是正向执行还是反向执行关键取决于进入子过程后DIR 的取值，如为1则正向执行，如为－1则反向执行。可以发现在DIR 取值为1和－1时，正向乘法所对应的跳转指令是不同的。为方便起见，余下部分以Multx代表执行执行乘法指令，以Multx－1代表反向执行执行指令。同样，Divx 代表正向执行除法指令，以Divx－1代表反向执行除法指令。

2.1.4 指令执行效果

除法指令和乘法指令正向执行效果如表4所示，反向执行效果只要交换表4中的前后状态即可得到。对于除法指令 （以20÷6＝3…2为例），执行前R3 存放被除数20，R2存放除数6，R1为0，执行后R3存放余数2，R2保持不变，R1存放商。对于乘法指令，执行前R3初值为2 （对应除法指令中的余数），R2存放被乘数，R1存放乘数，执行后R3等于2＋6＊3即20，R2保持不变，R1清零。容易发现，除法指令Divx和乘法指令Multx执行前后的寄存器状态正好相反，如将这两条指令看作是系统状态的变换函数，两者互为逆函数，即两条指令互为逆指令。需注意的是，在指令执行过程可以使用除R3、R2、R1以外的辅助寄存器，但为了逻辑可逆，这些寄存器在指令执行后需恢复为执行前的状态。

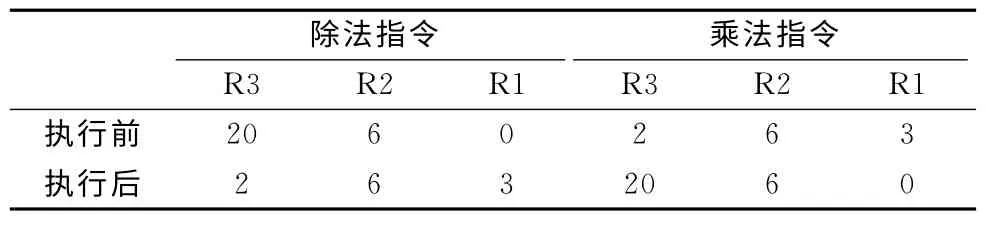
表4 乘除法指令执行效果

2.2 乘法指令的设计

乘法实现拟采用原码一位乘方法，但和传统方法略有不同。其主要思想是，从乘数低位开始，如当前位为1，将被乘数与部分积相加并消除乘数的当前位，然后再根据乘数高一位作类似操作，但被乘数须左移一位，直到乘数最高位为止。可逆乘法子过程的流程如图5所示，图中方框表示1个或1串指令，每一个方框都是对系统状态的可逆更新，为节约空间相邻方框间的箭头被略去，同样表示反向运行路线的虚线箭头也被略去。

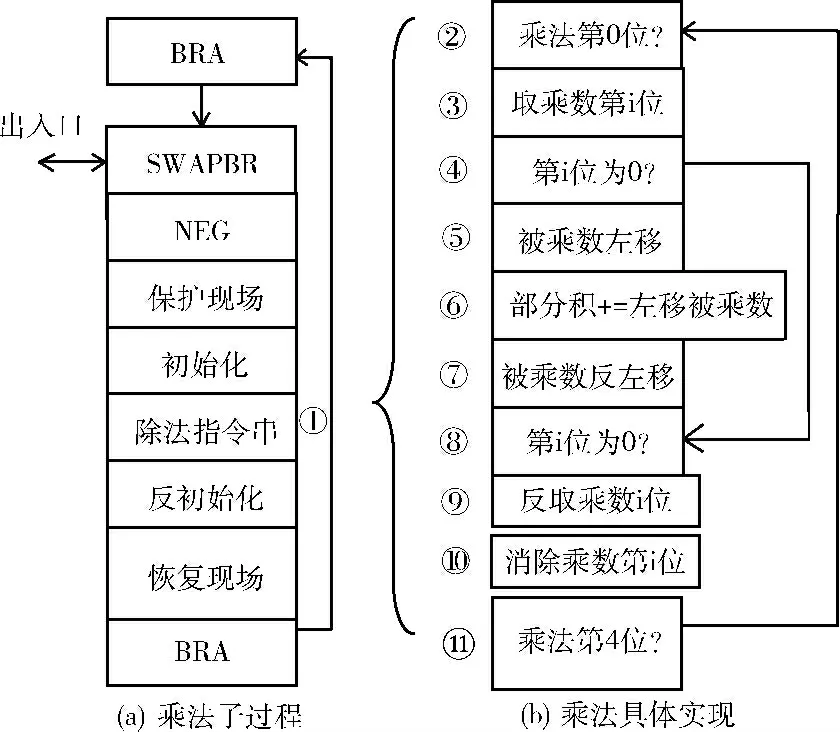
图5 可逆乘法子过程

图5 （a）展示了乘法子过程的整体结构，其中保护现场是将子过程中涉及到的辅助寄存器内容保存到堆栈中，恢复现场则相反；初始化操作为相关寄存器赋初值，反初始化将相关寄存器值恢复为零。图5 （a）中①处除法指令串的实现细节在图5 （b）中展示，其中②和瑏瑡是控制循环开始与结束的条件转移指令对；③处取乘数第i位；④到⑧是根据乘数第i位是否为零决定是否在部分积中加上左移的被乘数；⑨处消除③处对系统状态的更新。⑩处通过一串指令消除乘数的第i位以使乘数寄存器在循环结束后值为零。

可逆乘法子过程的代码如图6所示，为节约空间省去保护现场和恢复现场相关代码。图6中各寄存器作用如下：R0存放常量0，R1、R2和R3分别对应乘法指令的3个参数：乘数、被乘数以及初值／乘积和，R4暂存BR 寄存器内容，R5暂存常量4 （表示最大位数），R6暂存用于取乘数第i位的掩码，R7暂存循环计数器 （＜4），R8暂存乘数的第i位，R9暂存移位后的乘数。

图6 可逆乘法子过程代码

除保存参数的R1、R2、R3 寄存器外，其它辅助寄存器R0、R4－R9应在使用前通过EXCH 指令进行现场保护（篇幅原因省去相关代码），随后这些寄存器内容将为零，在子过程执行过程中其内容可能会发生改变，2.1.3 要求在子过程返回前须将这些辅助寄存器再次清零，然后再对这些寄存器恢复现场。图6中02行代码是乘法子过程的入口和出口。03行代码将进入子过程的跳转偏移量取负，为将来再次返回到调用点做准备。04－05行代码初始化R5、R6寄存器。06行代码表示循环入口条件。07－13 行代码表示在第i次循环中如乘数R1当前位为1，则将被乘数R2左移i－1位并与R3相加，并将结果保存在R3中。14－20行代码表示在第i次循环中消除乘数R1第i位以达到最终R1清零的目的。21行代码表示R6循环左移一位。22行代码表示循环计数器R7加一。23行代码表示循环出口条件。24－26代码将R5、R6 以及R7 清零，也称反初始化，R8和R9 寄存器循环前后其值未发生变化，所以无需反初始化。

需特别注意的是，07行代码是进行与运算的扩展指令，按上文可逆编程原则 （1）在13行再次使用该指令以清空R9。类似的扩展指令对还有09行和11行、14行和20行。

2.3 除法指令的设计

除法的实现采用恢复余数法，但和传统的恢复余数法略有差别，其运算过程如图7所示 （以10101111÷1010为例）。该运算共有8步操作，每一步将被除数R3寄存器和辅助寄存器R8共同左移一位，并将R3的最高位移入R8的最低位，然后将R8寄存器与除数寄存器R2相减，如果结果大于等于零，则将商R1左移一位并在末尾上一，否则商左移一位末尾上零并将R8与R2相加以恢复余数。第八步操作执行后，R1中存放商，交换R3和R8的值，从而使R8清零，R3中存放余数。

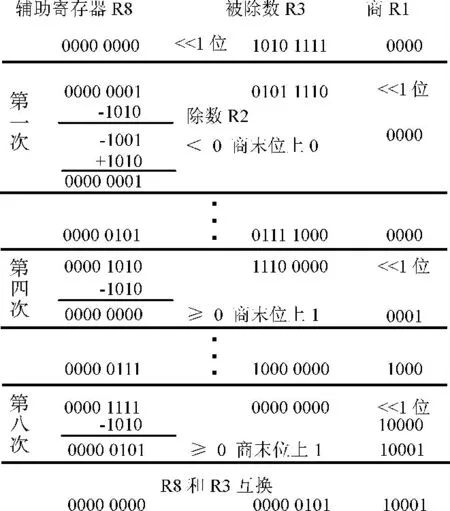
图7 恢复余数法

可逆除法子过程如图8所示。图8中各寄存器作用如下：R0存放常量0，R1存放商，R2存放除数，R3存放被除数／余数，R4暂存BR 寄存器内容，R5暂存循环计数器，R6暂存被除数最高位，R7暂存常量8，R8为如图7所示的辅助存储器，R9暂存被乘数算术右移7位的结果，R10暂存R8或R1最后一位。

02行代码为除法子过程的出入口。04 行代码初始化R7寄存器。05行代码表示循环入口条件。06－09行代码将R8寄存器左移一位，并将被除数R3寄存器的最高位移入R8的最低位。10－15行代码表示如R8最低位为1 （由R3最高位移入），则消去R3中最高位的1并循环左移一位以得到R3算术左移一位的结果。16行代码将商R1逻辑左移1位。代码17将R8与除数R2相减，并将结果保存到R8。18－20代码表示若R8 大于等于零，则在商的末尾加1。21－25行代码表示若R8小于零，则要恢复余数。26行代码使循环计数器R5加1。27行代码表示循环退出条件。28行代码表示交换R3和R8寄存器的内容，实际上PISA 指令集中无EXCHR 指令，需通过使用3次异或指令实现R3和R8交换，此处使用EXCHR 代替3次异或指令。29 行代码恢复R7的初值0，也称为反初始化。

图8 可逆除法子过程

2.4 算法分析

图6和图8所示的乘法子过程和除法子过程中从单条指令到整体结构均逻辑可逆。因此对于乘法子过程而言，正向执行表示做乘法运算，反向执行表示消除乘法运算对系统状态的更新，效果上类似于对乘法运算后的寄存器作除法运算。对于除法子过程而言，正向执行表示做除法运算，反向执行表示消除除法运算对系统状态的更新，效果上类似于对除法运算后的寄存器作乘法运算。

最好和最坏情况下两个子过程循环体中的加法、移位等操作次数统计如表5所示。统计时需注意，除法子过程18－20行代码和22－24 行代码是互斥的，不可能同时执行。

表5 子过程循环中的关键操作次数

从表5可得，无论在最好情况还是最坏情况下，乘法效率略高于除法。

3 仿真与仿真结果

3.1 仿真平台

根据可逆处理机Pendulum 的架构，为可逆指令集的运行设计了一个软件仿真平台。平台如图9所示，以Java类模拟Pendulum 各主要部件，通过类中的成员方法实现各部件的功能。

图9 运行可逆指令集的仿真平台

图9中控制器的主要作用如下：根据PC寄存器取出指令并解析，然后根据指令性质调用运算器中相应方法处理数据；指令执行后，根据BR 寄存器、DIR 方向位的状态更新PC寄存器。运算器中包含若干执行相应运算的成员方法，一般情况下每条指令对应两种运算方法，分别表示正向语义和反向语义，但有些指令其逆指令为其本身 （如EXOR指令），仅对应运算器中的一个方法，该方法既表示正向语义，又表示反向语义。寄存器组包含32 个8 位通用寄存器，但在乘除法指令中只用到其中11 个 （R0－R10）。DIR方向位表示仿真平台执行程序的方向，为1时正向执行，为－1 时反向执行，在运行过程中可以被随时切换。

3.2 仿真结果

仿真平台上正向或反向执行乘法或除法子过程时前后的寄存器状态如图10 所示 （数值以16 进制表示），其中“Multx”表示正向执行乘法指令， “Multx－1”表示反向执行乘法指令， “Divx”表示正向执行除法指令， “Divx－1”表示反向执行除法指令。

图10 乘法指令和除法指令正／反向运行效果

从图10 （a）可发现，在相同寄存器初态下正向执行乘法指令和反向执行除法指令取得的终态相同，即无论Multx还是DIVX－1，执行完毕后R3的值等于其初值与R2乘R1之和，而R2不变、R1清零。从图10 （b）可发现，在相同寄存器初态下正向执行除法指令和反向执行乘法指令取得的终态相同。如将Multx看作是系统状态的变换函数，则Multx和Divx－1等价，Divx和Multx－1等价，但这种等价关系有时需满足特定约束条件才能成立。这是由于乘法和除法指令设计时在参数上取值区间的不对称引起的，第一种不对称存在于参数1即R3，除法运算得到的余数R3必然小于除数R2，而在乘法运算中R3的初值没有这个限制；第二种不对称存在于参数3即R1，本文设计的乘法指令局限于4×4 （即乘数R1最大为15）运算，而8÷4除法指令的商可能超过4 位 （如图7 所示）。由于以上两种不对称性，正向运行模式下 （DIR 预设为1）仅在满足相应约束条件时程序中相关运算可被其等价运算替换，等价关系见表6。

表6 正向模式下乘法和除法操作的等价关系

从乘法和除法子过程的分析已知乘法效率略高于除法的事实。通过将除法运算替换等价的乘法运算可以提高程序效率。如表6所示，第3行和第4行的除法运算可被无条件地替换为相应乘法运算以提高程序效率。因此在正向模式下下，除法指令无存在必要性。

反向模式时 （即DIR 在程序执行过程中被设为－1），则按相反顺序执行指令串并按相反语义解释所遇指令，即相当于用逆指令取代当前指令。根据上述分析并通过反复试验得如表7 所示结论，形如inv （Multx）表示对Multx以相反语义进行解释，可以发现每个指令都对应两个逆指令。由于指令Multx和Divx都是通过可逆子过程实现的，因此表中第1、3、5以及7行容易理解。同样由于前述的两种不对称性，对第2、4、6 以及8 行指令反向解释时，只有满足相关约束条件时才能用逆指令替换。

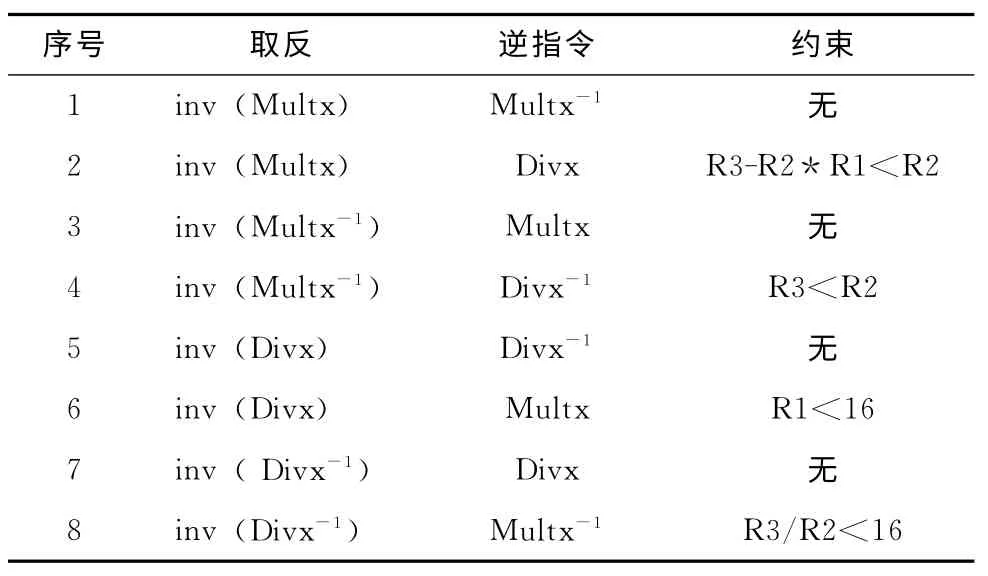
表7 DIR 方向位为－1时相关指令的逆指令

根据表7以及乘法比除法效率高的结论，在DIR 方向位为－1的前提下，并在满足相应约束条件时，将表中第6和8行的除法运算替换成相应乘法运算，可以有效提高程序运行效率。但在不满足约束条件的情况下除法运算不能被乘法运算取代，因此DIR 为－1 时除法指令有其存在必要性。

4 结束语

本文为PISA 指令集扩充的乘法指令和除法指令均为可逆指令，即既支持正向执行，又支持反向执行。另外，正向的乘法指令和反向的除法指令以及反向的乘法指令和正向的除法指令在满足特定约束条件时相互等价，即乘法指令和除法指令在满足特定约束条件时互为逆指令。利用乘除法指令互为逆指令的特性，根据乘法指令的效率要高于除法指令的结论，在满足表6和表7相关约束时尽量使用乘法指令实现乘除法操作，有助于提高程序运行效率。

最后，本文虽然是通过子过程实现了乘法指令和除法指令，但其本质上是一种软件形式的可逆串行乘法器和除法器，因此其设计思路可以指导相关硬件运算器［8－10］的实现。

［1］Saeedi M，Markov IL.Synthesis and optimization of reversible circuits－a survey ［J］.ACM Computing Surveys，2013，45（2）：1－34.

［2］Hirata Y，Nakanishi M，Yamashita S，et al.An efficient conversion of quantum circuits to a linear nearest neighbor architecture［J］.Quantum Information ＆ Computation，2011，11（1）：142－166.

［3］ZHU Pengcheng，GUAN Zhijin，WEI Lihua.Design of reversible programming language R－JAVA and its language processing system ［J］.Computer Engineering and Design，2013，34 （10）：3502－3510 （in Chinese）. ［朱鹏程，管致锦，卫丽华.可逆编程语言R－JAVA 及其语言处理系统的设计 ［J］.计算机工程与设计，2013，34 （10）：3502－3510.］

［4］Axelsen HB，Glück R，Yokoyama T.Reversible machine code and its abstract processor architecture ［G］.LNCS 4649：Computer Science－Theory and Applications. Heidelberg：Springer，2007：56－69.

［5］LI Bin，YANG Jiaqi.Computational model and simulation analysis for container terminal operation systems under Harvard architecture ［J］.Computer Integrated Manufacturing Systems，2013，19 （9）：2300－2314 （in Chinese）. ［李斌，杨家其.哈佛体系结构下的集装箱码头操作系统计算模型与仿真分析 ［J］.计算机集成制造系统，2013，19 （9）：2300－2314.］

［6］Thomsen MK，Axelsen HB，Gluck R.A reversible processor architecture and its reversible logic design ［G］.LNCS 7165：Reversible Computation.Heidelberg：Springer，2012：30－42.

［7］Axelsen HB.Clean translation of an imperative reversible programming language［G］.LNCS 6601：Compiler Construction.Heidelberg：Springer，2011：144－163.

［8］Dastan F，Haghparast M.A novel nanometric reversible signed divider with overflow checking capability ［J］.Research Journal of Applied Sciences，Engineering and Technology，2012，4 （6）：535－543.

［9］Dastan F，Haghparast M.A novel nanometric fault tolerant reversible divider ［J］.International Journal of the Physical Sciences，2011，6 （24）：5671－5681.

［10］Moallem P，Ehsanpour M.A novel design of reversible multiplier circuit（technical note）［J］.International Journal of Engineering－Transactions C：Aspects，2013，26 （6）：577.