基于小波分析的ARMA－SVR网络流量预测方法

刘 亮，江汉红，王 洁，芮万智

（海军工程大学 舰船综合电力技术国防科技重点实验室，湖北 武汉430033）

0 引 言

网络流量的传输受到网络拓扑结构、通信协议和转发方式等因素的影响，因此其特性能够在一定程度上反映出所承载的网络业务的行为，分析和预测网络流量的行为特性对于实现网络数据传输的可靠性和网络资源分配的合理性具有重要意义。目前已有相关预测模型主要可以分为以下几大类型：

（1）线性预测模型。早期学者在进行网络流量建模时，通常假设网络流量服从Poisson分布，或近似为Markov过程，多采用基于自回归或自回归滑动平均的线性预测模型［1］。

（2）非线性预测模型。目前常用的非线性预测模型有人工神经网络模型［2－4］、灰色预测模型［5］、混沌模型［6］、支持向量回归机模型［7］等，各种算法都有较好的适用性，但也存在自身固有的问题和改进的空间。

（3）组合预测模型。这类模型大体上又可分为线性组合预测模型和小波分解组合预测模型。与线性组合方式相比，由于小波分解能够将网络流量数据分解成为多个成分较为单一的分支流量信号，因此成为了当前网络流量预测模型的主要研究方向［8－10］。

在上述研究基础上，本文提出一种基于小波分解的ARMA－SVR组合预测模型，该模型综合了ARMA 模型和SVR 模型的优点，在提高预测精度的同时保证了计算速度，是一种行之有效的网络流量预测方法。

1 小波变换与ARMA、SVR 预测建模

1.1 小波变换与多分辨分析

小波变换是一种非线性序列分析方法，适合对非平稳数据进行分解处理。小波变换可以把具有复杂特性的网络流量进行分解，得到频率特性相对比较单一、更易于预测的时间信号，然后建立能够刻画不同特性的对应信号模型，可以得到能够反映网络流量总体趋势的预测值和各个细节的预测值，从而实现对网络流量的预测。流量信号x（t）的小波变换可以表示为

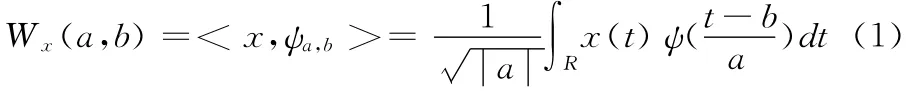
重构公式为

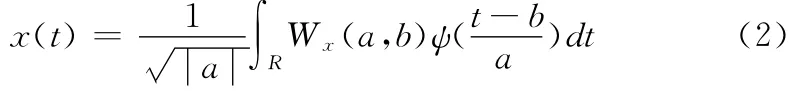
多分辨分析是小波分析中一种对信号的空间分解方法。其主要思想是把有限能量的信号空间L2（R）分解为一系列具有不同频率分辨率的子空间，小波变换将原始流量信号x（t）∈L2（R）通过高通和低通两个滤波器逐一投影到各个子空间，得到低频信号和各层高频信号的投影。低频信号是网络流量的主体趋势项部分，该部分反映的是网络流量整体的变化趋势特征；高频信号是网络流量的随机性部分，反映随机扰动等动态因素对网络流量的影响，是对趋势项部分的细节补充。对各个投影部分进行线性组合后可以实现对信号x（t）的还原。这样通过对x（t）在每个子空间投影的分析和预测就可以得到其在信号空间L2（R）的预测值。一个三层小波分解结构如图1所示。

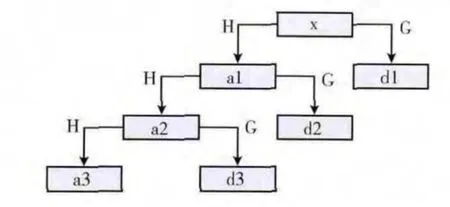
图1 小波分解树

小波分析中一般采用Mallat算法对流量信号x（t）进行分解和重构。

分解

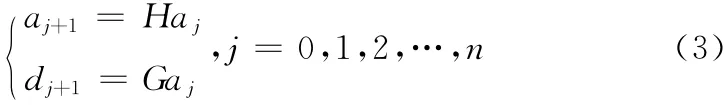
重构

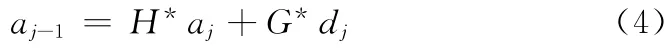
式中：H——一低通滤波器，G——一高通滤波器，H＊、G＊——H 和G 的对偶滤波器；aj——x（t）经过小波分解得到的低频系数，dj——高频系数。

1.2 自回归－滑动平均 （ARMA）预测模型

如果一个流量信号在t时刻的流量xt不仅与它以前时刻t－1，t－2，……的流量xt－1，xt－2……有直接关系，而且与以前时刻t－1，t－1，……的系统扰动项εt－1，εt－2，……存在一定的相关关系，那么这类流量信号模型称为自回归滑动平均 （ARMA）模型。其一般形式为

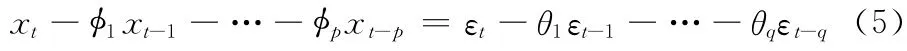
式中：εt——具有0均值的正态分布白噪声。

即xt＝（B）θ（B）εt，记作ARMA（p，q）。

ARMA 模型具有自相关函数 （ACF）和偏自相关函数（PACF）拖尾的特性，如果仅自相关函数或者偏自相关函数具有拖尾特性，则ARMA 模型退化成为自回归 （AR）模型或者滑动平均 （MA）模型，具体判定准则见表1。ARMA 模型基本的建模步骤如下：首先计算样本流量的自相关函数和偏自相关函数，根据其截尾特性和拖尾特性来对模型的进行辨识和定阶：若ACF函数具有截尾特性则使用MA 模型，若PACF函数具有截尾特性则使用AR 模型，若两者都具有拖尾特性则使用ARMA 模型；继而使用非线性最小二乘法估计该ARMA 模型中的未知参数的值，最后根据完成后的模型对流量进行预测，并根据需要计算残差，看其是否满足白噪声的特性。

1.3 支持向量回归机 （SVR）预测模型

支持向量回归机的基本思想是寻找一个非线性映射φ（x）：R →F，将低维空间R 映射到高维特征空间F，并在高维特征空间中对网络流量x（t）进行估计

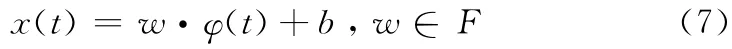
式中：w——权值向量，b——偏置项。

通过式 （7）可以将一个低维空间内的非线性回归问题转化为一个高维特征空间的线性回归问题，因此支持向量回归机模型可以表示为一个二次规划问题

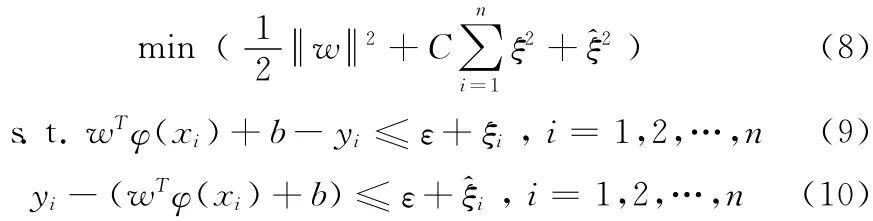
式中：ξi、——松弛变量；ε＞0称为不敏感参数，其大小决定了对网络流量的拟合精度。采用Lagrange乘子法对该二次规划问题进行求解可得

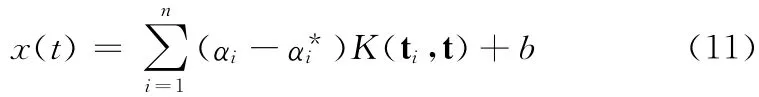
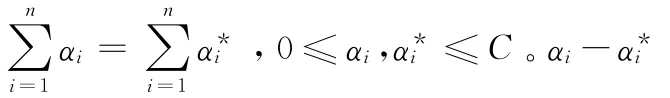
C 和ε是支持向量回归机算法中两个需要调整的重要参数，对流量预测模型的性能具有较大影响，可以通过调整C和ε两个参数使得样本流量预测的结构风险 （即泛化误差上界）最小。相比于人工神经网络的经验风险最小准则，其优化目标是即训练误差最小，容易陷入局部极小点，造成过拟合而影响模型的泛化能力，因此支持向量回归机在理论上具有更好的泛化性能。一般情况下优先选择较小的C 参数，这样可以减少支持向量的数量，从而有效地减少计算量。

1.4 网络流量的ARMA－SVR建模

本文中采用ARMA 模型与支持向量回归机的组合模型，综合双方各自的优点，在更精确地逼近原始流量数据的同时，有效地增加了模型的计算速度。本文的预测模型结构框架如图2所示。

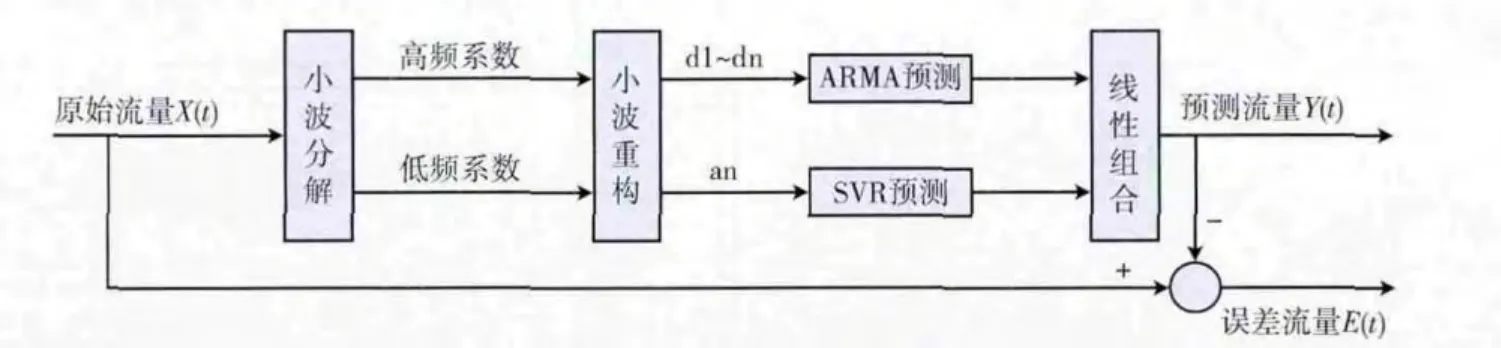
图2 ARMA－SVR组合预测模型框架

建模步骤：

（1）采集待分析的网络流量数据，得到原始的网络流量时间信号，从中选择一部分作为训练样本，一部分作为测试样本；

（2）选择db4母小波函数对网络流量的训练样本部分进行5层小波分解，得到训练样本的各高频系数序列和低频系数序列；

（3）对各高频系数序列和低频系数序列采用小波逆变换进行重构，得到低频分量和各高频分量；

（4）分别采用SVR 方法和ARMA 方法对低频分量和各高频分量进行建模，将各分量的预测结果按下式进行线性组合后得到网络流量的最终预测结果

（5）将网络流量的预测结果与实际网络流量对比，进行预测误差分析。

2 仿真实验分析

2.1 实验数据来源

仿真实验的数据来源于某局域网系统中的一台骨干交换机，通过网络流量监测软件采集了该交换机某上联端口2013年4月6日的网络流量。由于原始数据流量较大，并且具有较强的随机性，因此从原始数据中随机连续选取2000个数据点作为的实验数据，绘制其波形如图3 所示。并从中选取前1800个点作为训练样本进行建模，后200个数据作为测试样本验证模型的有效性。

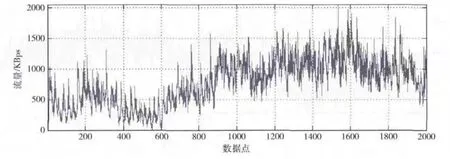
图3 采集的实际网络流量数据

2.2 原始流量的小波分解与重构

针对前1800个训练样本数据点，采用快速Mallat算法对其进行5层小波分解，再分别对每个分支进行重构，分解和重构均选用db4母小波函数，得到的网络流量的各层近似分量a1～a5如图4左边所示，各层细节分量d1～d5如图4右边所示。

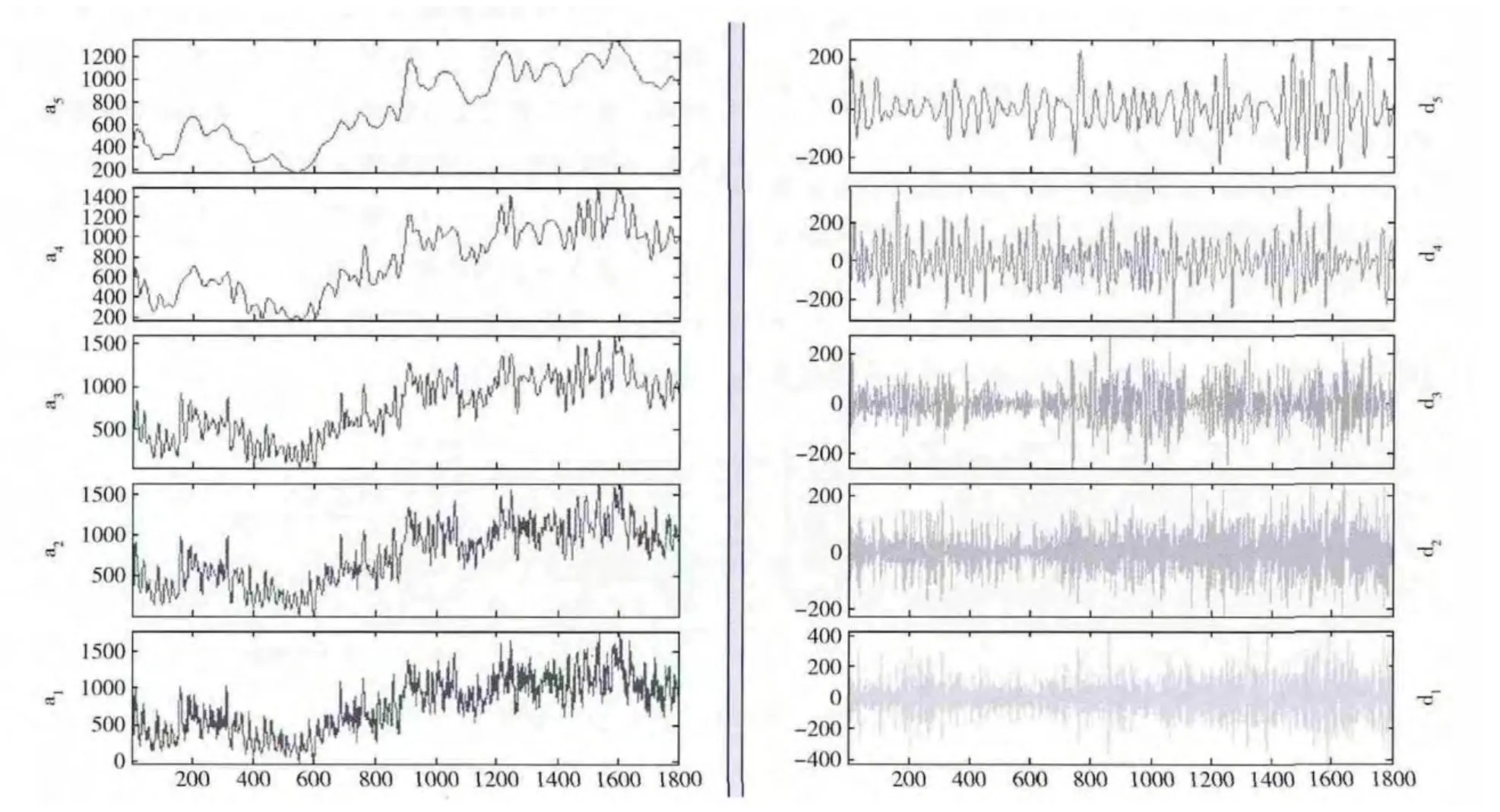
图4 样本流量经过小波分解得到的各层近似分量和细节分量

从图4中左边可知，近似分量信号a1～a5变得逐渐平滑，体现出了网络流量变化的主体趋势。近似分量信号在进行流量合成的线性组合运算中只需要使用a5 层的流量数据。

2.3 模型参数选择与预测结果

对于细节部分d1～d5采取ARMA 模型进行预测。由于ARMA 模型适用于平稳时间序列的预测分析，具有良好的线性特性，可将所有细节部分求和后采用一个ARMA 模型进行预测。令流量信号d＝d1＋d2＋d3＋d4＋d5为细节部分之和，通过计算流量信号d的自相关函数和偏自相关函数，根据两者的拖尾特性和截尾特性初步判定细节流量信号d 符合为ARMA（3，0）模型，即AR（3）模型，并通过Matlab对细节部分流量进行建模预测，得到d的预测结果。

对于趋势部分a5采取SVR 模型进行预测。将a5样本流量进行归一化后输入到libsvm 工具箱中，核函数选择径向基 （RBF）函数。为了对SVR 模型的参数进行寻优，通过多次测试和调整，最后确定SVR 模型的其它参数取ε＝0.2和C ＝10，径向基函数选取g ＝0.5。建立支持向量回归机仿真并进行训练，得到趋势部分a5的预测结果。

将SVR 模型和ARMA 模型得到的预测结果按照式（12）进行线性组合后得到流量的最终预测结果，与实际流量进行对比，得到的结果如图5所示。

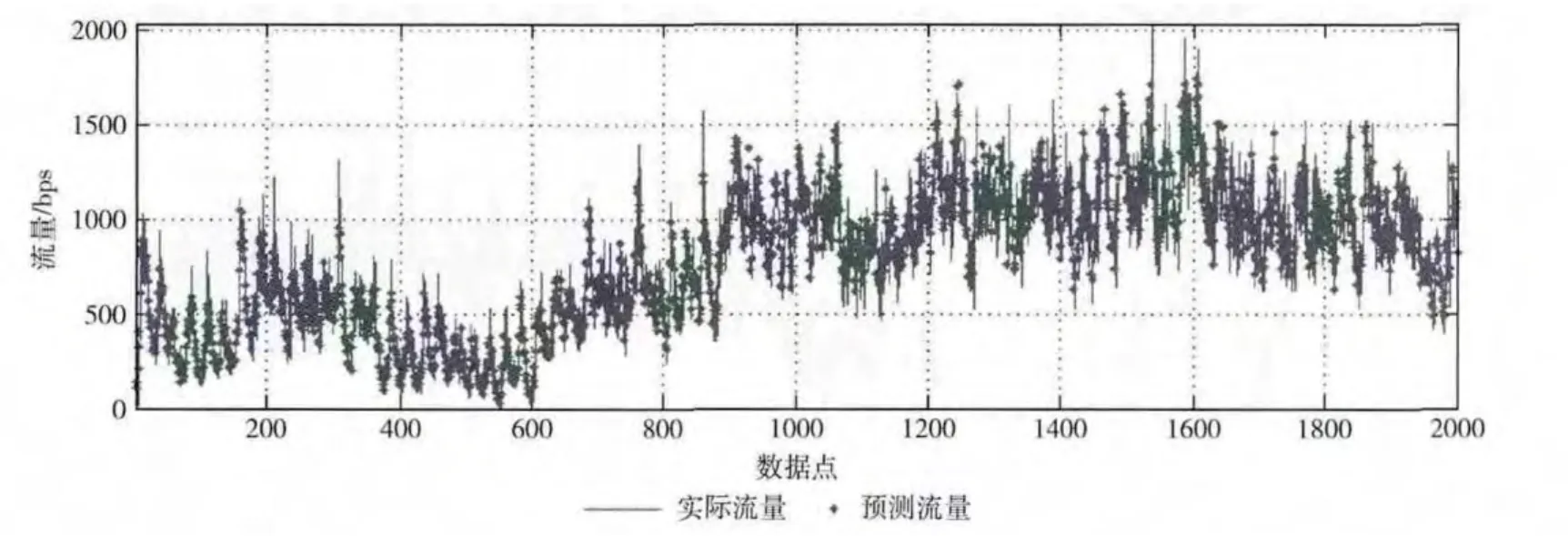
图5 流量预测值与实际值比较结果

从图5中的拟合结果可以看出，由于采用了组合预测的方法，本模型对于样本流量主体趋势和细节部分都拟合的比较好，这是因为小波分解将高随机性和非线性的网络流量信号分解成多个频率成分较为单一的流量信号，降低了不同频率部分信号之间的干扰，从而有效地提高了预测精度。不过随着时间的增加，由于流量数据的起伏较大，对于测试流量误差也逐渐有所增大。

2.4 实验结果分析对比

为了检验本文模型的预测效果，拟采用单一ARMA 预测模型、单一SVR 预测模型和BP神经网络模型进行对比，并采用平均相对误差MRE 对各种模型的预测结果进行评价。MRE定义如式 （13）所示

通过计算各模型预测结果的MRE可以得到误差对比结果见表1。

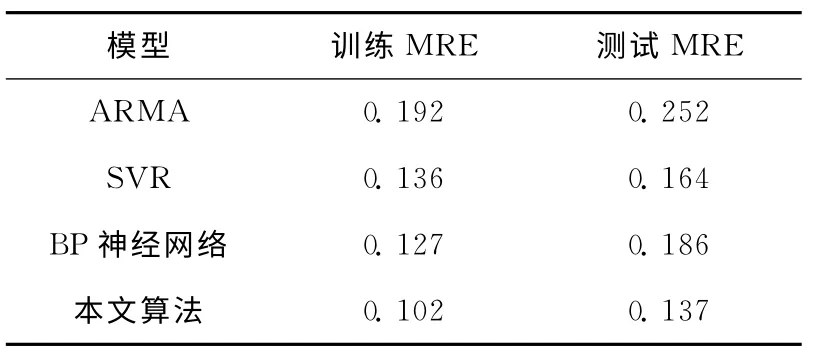
表1 各模型的预测误差对比

从表2的平均误差值对比结果可知，采用SVR 算法的网络流量预测模型与其它模型相比，具有预测精度较高和泛化能力较好的优点；而ARMA 模型会平滑预测数据的波动，对于线性特性较好的流量具有较好的预测效果，较适合于短时预测，且具有预测精度高、计算速度快的特点，对于具有强烈波动和非线性的流量的预测误差较大，所以不宜单独使用；而神经网络虽然在训练过程中的样本拟合误差较小，但是测试样本误差变大，在实际使用中预测效果不如SVR 方法和本文算法好。本文采用了基于小波分解的组合预测算法，通过对网络流量进行分解，针对不同层的特点综合了ARMA 模型和SVR 模型的优点，进一步提高了网络流量的预测精度。不过由于网络流量的随机性较大，用于仿真实验的训练数据和测试数据较多，要想准确地预测网络流量的长期行为还有一定困难。在上述仿真计算的基础上，经过多次对比计算发现，以下因素对模型的预测结果具有一定的影响：

（1）分解层数的影响：随着分解层数的增加，预测误差逐渐减小并趋于稳定。这是由于流量信号主体部分在于近似信号和低层细节信号部分，而分解层数的增加只是对于高层细节部分做进一步的分解，由于这一部分的信号占整体流量信号的比例较小，因而这一部分的预测误差对整体流量的预测影响不大，所以总体预报误差将不随分解尺度而有太大的改变。相反，随着分解层数的增加，计算量会有所增大，因此不宜设置较高的分解层数。

（2）母小波函数的影响：由于母小波函数种类较多，每种母小波函数都有其各自的特点，最理想的情况是选择与网络流量起伏特点近似的母小波函数，然而目前情况下只能采用多次实验对比的方法或者依靠经验来选择。

3 结束语

本文提出一种基于小波分析的网络流量组合预测模型，通过小波变换把网络流量分解成低频近似信号和多个高频细节信号之和，采用SVR 模型和ARMA 模型分别对低频信号和高频信号进行拟合，然后将各个模型的预测结果进行线性组合后得到网络流量的预测值。仿真实验结果表明，相比于其它方法，该预测模型可有效结合两种预测模型的优点，克服单一预测模型的不足，具有更高的预测精度，改善了网络流量的预测性能。为了进一步提高实际流量的预测精度，可以对模型采用实时修正的方法，不过由于SVR 算法复杂度较高，如何提高本算法的实时性是下一步需要重点研究的方向。

［1］GU Zheng，CHU Baojin，JIANG Huikun.WAVELET—ARMA method in the non－stationary time series and its application［J］.Systems Engineering，2010，28 （1）：73－77 （in Chinese）. ［谷政，褚保金，江惠坤.非平稳时间序列分析的WAVELET—ARMA 组合方法及其应用 ［J］.系统工程，2010，28 （1）：73－77.］

［2］LI X Y.Prediction of traffic flow base on neural network［C］／／Intelligent Computation Technology and Automation，2009：374－377.

［3］Ardhan S，Satsri S，Chutchavong V，et al.Improved model for traffic fluctuation prediction by neural network ［C］／／Proceedings of International Conference on Control Automation and Systems，2007：122－125.

［4］ZHU L，QIN L，XUE K，et al.A novel BP neural network model for traffic prediction of next generation network ［C］／／Natural Computation，2009：32－38.

［5］MA Hualin，LI Cuifeng，ZHANG Liyan.Network traffic prediction based on grey model and adaptive filter［J］.Computer Engineering，2009，35 （1）：130－131 （in Chinese）.［马华林，李翠凤，张立燕.基于灰色模型和自适应过滤的网络流量预测［J］.计算机工程，2009，35 （1）：130－131.］

［6］LUO Yunqian，XIA Jingbo.WANG Huanbin.Application of chaos－support vector machine regression in traffic prediction ［J］.Computer Science，2009，36 （7）：244－245 （in Chinese）.［罗赟骞，夏靖波，王焕彬.混沌－支持向量机回归在流量预测中的应用研究［J］.计算机科学，2009，36 （7）：244－245.］

［7］YANG Mei，ZHAO Xiuli，LIU Yu.Research on wavelet decomposition in prediction of time series［J］.Information Technology and Informatization，2011，33 （2）：45－48 （in Chinese）.［杨玫，赵秀丽，刘瑜.时间序列预测问题中小波分解的应用研究 ［J］.信息技术与信息化，2011，33 （2）：45－48.］

［8］LI Xiaohang，LIU Yuan，LIU Yuanzhen.Research on network traffic combination prediction method based on wavelet multi scale analysis［J］.Microelectronics ＆Computer，2008，25 （1）：130－133 （in Chinese）.［李小航，刘渊，刘元珍.基于小波多尺度分析的网络流量组合预测方法研究 ［J］.微电子学与计算机，2008，25 （1）：130－133.］

［9］LIU Yuan，WANG Peng.Combining wavelet transform and Bayesian least squares support vector machines to predict network traffic ［J］.Application Research of Computers，2009，26 （6）：2229－2231 （in Chinese）.［刘渊，王鹏.融合小波变换与贝叶斯LS－SVM 的网络流量预测 ［J］.计算机应用研究，2009，26 （6）：2229－2231.］

［10］GONG Linming，ZHANG Zhenguo.Combination prediction model to network traffic based on grey－wavelet［J］.Computer Engineering and Design，2010，31 （8）：1660－1661 （in Chinese）.［巩林明，张振国.基于灰色小波的网络流量组合预测模型 ［J］.计算机工程与设计，2010，31 （8）：1660－1661.］