凸轮X-C联动磨削廓形误差迭代学习控制

陈砚坤，韩秋实，彭宝莹，夏怀健

CHEN Yan-kun, HAN Qiu-shi, PENG Bao-ying, XIA Huai-jian

（北京信息科技大学 机电工程学院，北京 100192）

0 引言

随着现代制造业的发展，制造业正向着高速、高精密的方向发展，这就导致对各类零部件的精度要求越来越高，并且对零部件的形状要求也越来越复杂。凸轮作为复杂型线零部件的一种，应用十分广泛，如汽车发动机的活塞、机械轴等[1]。凸轮加工精度直接影响着机械传动的准确性。目前，加工凸轮的最好方法是磨削，通过工件旋转和砂轮的移动将凸轮磨削出，这种加工方式称为X-C轴联动加工。通过联动的方式加工零件时，各加工轴的跟踪误差的大小对凸轮的廓形有着直接影响，特别是在高速进给过程中，会引起加工轴的跟踪误差，从而增大廓形误差，降低加工精度。为提高凸轮轮廓加工精度，减少廓形误差，本文引入了迭代学习控制方法。

迭代学习控制的控制律有多种，目前最为常用的是PID控制率，PID型迭代学习控制既有PID控制的简单灵活等特点，又有迭代学习控制的快速、自适应性强的特点[6]。本文首先根据凸轮廓形误差模型设计出X、C单轴的PID型迭代学习控制器，再利用MATLAB建立凸轮X-C轴联动仿真模型，验证通过使用迭代学习控制减小单轴跟踪误差进而减小廓形误差的的可行性。

1 PID型迭代学习控制器设计

1.1 迭代学习控制器设计思路

迭代学习控制原理结构图如图1所示，其中k是迭代的次数，uk(t)是第k次迭代的输入，yk(t)是第k次迭代的输出，yd(t)是期望输出，ek(t)是第k次的误差。第k次迭代的输出yt(t)与期望输出yd(t)相比较得到误差ek(t)，再通过迭代学习控制律得到补偿量，在与uk(t)相加得到第k+1次迭代的输入uk+1(t)。通过这种反复迭代学习使得实际输出无限逼近期望输出。

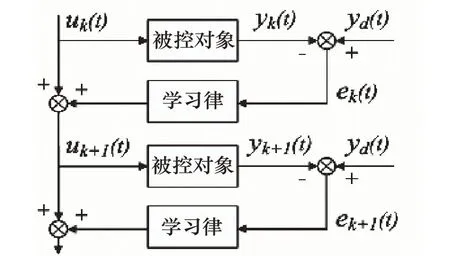
图1 迭代学习结构图

1.2 PID型迭代学习控制率

PID迭代学习控制律为：

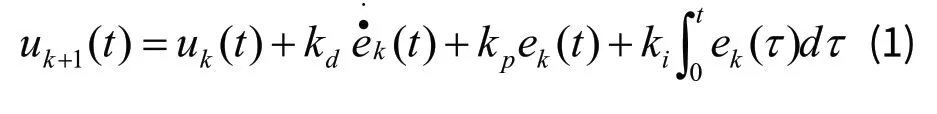
其中，kd、kp、ki分别为PID微分、比例和积分参数。

PID型迭代学习控制律的设计就是如何确定kd、kp、ki这三个参数的过程。本文采用闭环PID型迭代学习控制控制率，目前对于闭环迭代学习控制没有直接方法得出以上三个参数，只能通过反复凑试的方法得出。实验凑试法是通过闭环运行，观察系统的学习过程曲线，然后根据各参数的调节作用，反复测试，直至到达理想相应为止，从而确定三个参数的大小。

图2 凸轮磨削仿真模型示意图

2 凸轮X-C联动磨削仿真模型的建立

2.1 凸轮廓形误差模型[4]

设凸轮轮廓极坐标为ρ=ρ(φ)，轮廓X-C加工的运动规律为：

其中：

X为X轴位置坐标；

C为C轴位置坐标；

β=arctg(-dρρdφ)；

Rw为砂轮半径（mm）；

αA=arctg(ρcosβ(ρcosβ+Rw))。

X轴跟踪误差引起的凸轮廓形误差εx为：

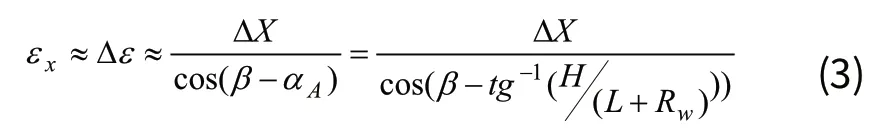
其中，ΔX为X轴跟踪误差。

C轴跟踪误差引起的凸轮廓形误εc为：

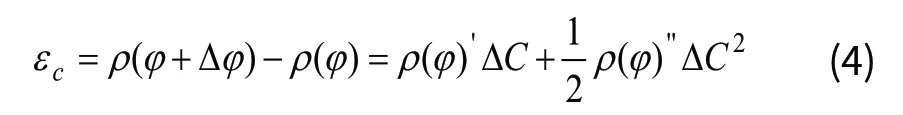
其中，ΔC为C轴跟踪误差。

凸轮轮廓X-C联动加工廓形误差ε为：

2.2 磨削仿真模型

根据凸轮廓形误差模型，利用Simulink建立磨削仿真模型如图2所示，将X、C位置指令以及凸轮极坐标作为输入，其中X、C轴位置指令分别为X、C轴的期望输出，将每次迭代得到实际输出与期望输出比较，得到误差，通过迭代学习律得到补偿量，在与输入结合得到新的输入，进而减小X、C跟踪误差，通过若干次迭代学习后得到最终的X、C轴的跟踪误差和，根据X-C联动廓形误差模型建立仿真模块得到廓形误差。

3 仿真结果与分析

3.1 X轴跟踪误差

如图3所示为X轴经过若干次迭代学习实际输出逐渐逼近期望输出的过程，如图4所示经过若干次迭代迭代学习后最终得到的跟踪误差的大小。根据图3、图4可以看出，X轴的输出曲线随着迭代学习的次数在逐渐逼近期望输出，最终得到的跟踪误差大小还是很理想的。

图3 跟踪过程

图4 X轴跟踪误差

3.2 C轴跟踪误差

如图5、图6所示，同样可以得出C轴的输出曲线随着迭代学习的次数在逐渐逼近期望输出，最终得到的跟踪误差大小在理想范围内。

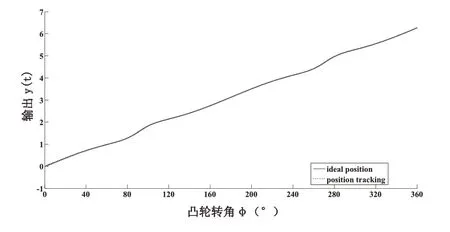
图5 跟踪过程

图6 C轴跟踪误差

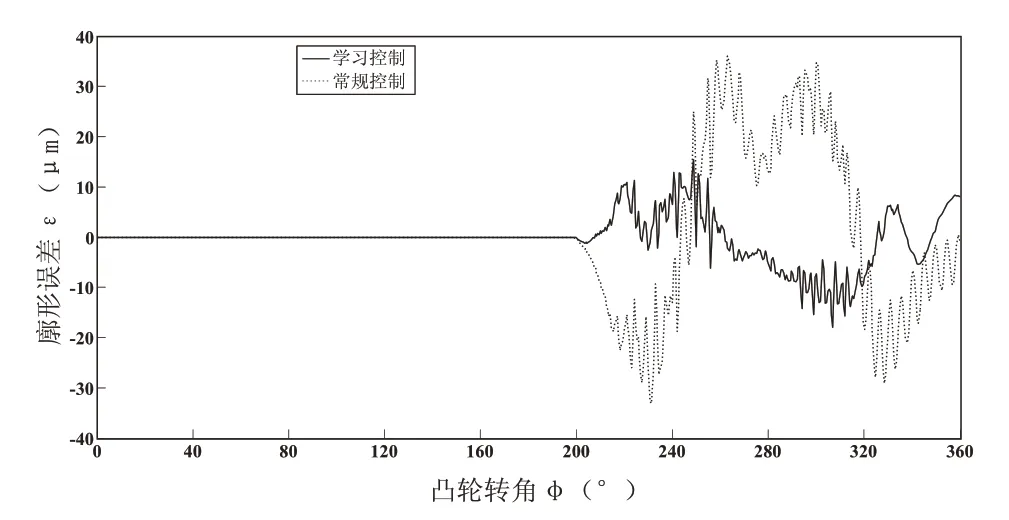
图7 廓形误差比较图

3.3 廓形误差

如图7所示，红线表示使用迭代学习控制最终得到的廓形误差大小，蓝线表示使用常规控制得到的廓形误差，比较可知，迭代学习控制相对于常规控制，更能有效减小廓形误差，提高凸轮磨削精度，可以看出误差减小量在一半以上。

4 结束语

在凸轮磨削加工过程中，通过使用迭代学习控制减少X、C轴的跟踪误差，进而减少廓形误差的方法是可行有效的，在一定程度上提高了凸轮的加工精度。

[1]李静,沈南燕,何永义.凸轮非圆磨削动态误差预测及补偿[J].设计与研究.2009.05.

[2]邵水军,闫勇刚.磨削加工技术的现状与进展[J].科技信息,2011,(4):138-140.

[3]吴刚华.曲轴非圆磨削轨迹控制关键技术[D].上海:上海大学,2006.

[4]Li K,Liao TW.Modelling of ceramic grinding processes Part I.Number of cutting points and grinding forces per.Grit[J].Journal of Materials Processing Technology,1977,65:1-10.

[5]彭宝营,蔡力钢,韩秋实.X-C直驱平台曲线轮廓磨削廓形误差非线性耦合控制[J].计算机集成制造系统.2014.02.

[6] 孙明轩,黄宝建.迭代学习[M].北京:国防工业出版社,1999.

[7]Hecker R L,Liang S Y,Wu X J,et al.Gringing force and power modeling based on chip thickness Analysis[J].Int J Adv manufacture technology,2007,33:449-459.

[8]Sun D,Tong M C.A synchronization approach for the minimization of contouring errors of CNC machine tools[J].IEEE Trans Auto Sci Eng,2009,6(4):720-729.

[9]Altintas Y,Khoshdarregi M.r.Contour error control of CNC machine tools with vibration avoidance[J].Ann CIRP vol,2012,61(1):335-338.

[10]谢胜利.迭代学习控制的理论与应用[M].北京:科技出版社,2005.