基于BFGS方法的双侧向测井几何因子表达式系数拟合

张融 彭泽波

（中国石油新疆油田分公司勘探开发研究院，新疆 克拉玛依 834000）

（新疆贝肯能源工程股份有限公司，新疆 克拉玛依 834000）

进行井眼、层厚等环境校正后，运用几何因子理论可以消除泥浆侵入影响，获得地层真电阻率值[1]。因此，利用几何因子进行地层电阻率校正时，首当其冲必须求得可靠的几何因子表达式系数。几何因子表达式有复杂的非线性特点，一般回归分析法不仅计算麻烦，而且精度不高。此时，最优化方法更为方便有效。测井解释中建立的最优化数学模型通常是带约束条件的非线性规划模型，或是无约束的非线性规划模型，本文针对所建立的数学模型主要采用适于多变量无约束非线性规划的拟牛顿方法中的BFGS法来得到双侧向测井的几何因子表达式系数。

1 模型与算法建立

由几何因子理论知，经过井眼和层厚等环境校正后，双侧向测井的几何因子取决于地层真电阻率，冲洗带电阻率及泥浆侵入带直径，即=f(Rt,Rxo,Di)。设有n个几何因子J，按最小二乘法得到如下式：

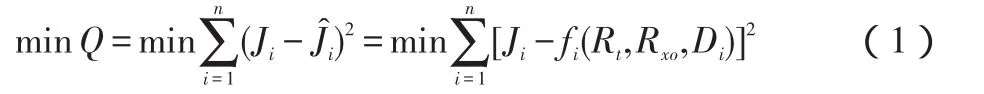
式子中，=fi(Rt,Rxo,Di)为几何因子拟合值，亦即所要求的几何因子拟合公式。当选用适当形式的拟合公式，将给定的一组Rt,Rxo,Di及相应几何因子数据代入式(1)，用最优化方法不断调整拟合系数，使目标函数残差平方和Q达到极小时，便可得出具体的几何因子拟合公式。本文采用的拟合公式形式如下[2]：

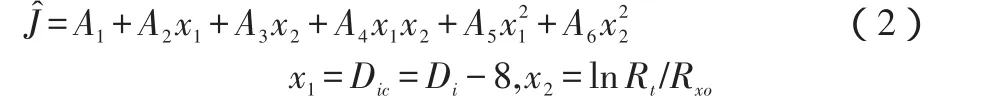
经上述分析知，本文所研究的问题属于多变量无约束非线性规划问题。一般来说，无约束多变量函数的最优化方法可分为采用目标函数导数的解析法与不用计算导数的直接法两大类。经观察，本文数学模型中的目标函数是连续的二次函数，可求导数，因此采用解析法较为方便省时。解析法中有最速下降法，牛顿法，拟牛顿法，共轭梯度法等等。综合各类方法的优缺点，本文选择了拟牛顿法中的BFGS方法并结合精确步长法。本文所用的迭代公式[3]为：

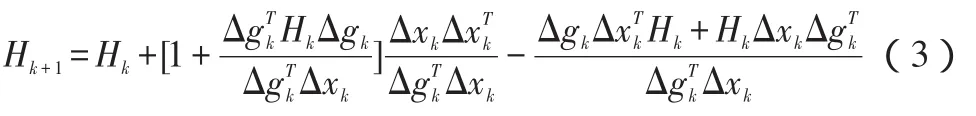
本文的主要算法如下：首先给定初始点和初始矩阵，且循环误差err大于0，k=0；一维搜索，确定最优步长λ并进行Hk+1计算；令k和k+1相等，返回上述步骤进行计算，直至计算次数达到某一规定值或前后两次计算之差小于循环误差后，迭代结束，输出真值。

2 实例分析

根据建立的模型和迭代算法，在MATLAB软件平台上编写程序，分别运行不同泥浆侵入半径条件下的双侧向测井几何因子表达式系数的计算。

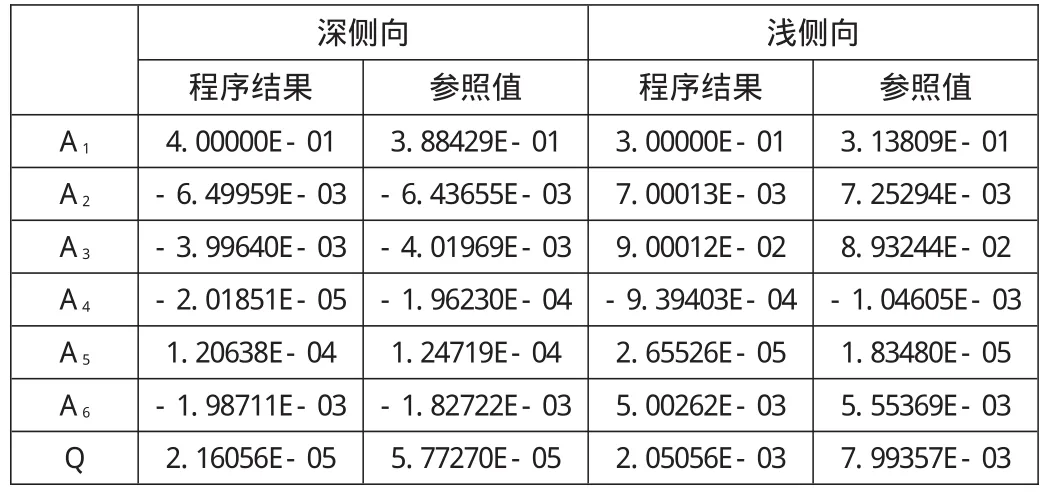
表1 双侧向测井几何因子表达式系数对比（Dic=50）

表1为泥浆侵入半径为50in时，程序结果与参照值[2]的双侧向测井几何因子表达式系数对照表，A为目标函数中未知数的最优解，Q为目标函数的极小值。目标函数极小值实际上就是拟合几何因子与真实几何因子差量的平方和，从目标函数极小值上分析自编程序的值更小，程序所得拟合公式的系数更为可信。

3 结语

3.1 初始值的选择很关键。虽然拟牛顿方法受初始点的影响明显小于其他最优化方法，但选择初值应尽量靠近真值。

3.2 拟牛顿算法中是否需要置Hn=I，x0=xn以重新迭代可视情况而定，若目标函数是较为标准的二次函数，且最优步长的结果较为精确时可省略这步以简化运算。

3.3 虽然自编程序得到的目标函数最优值更小，但验证应用效果还需要更多资料的对比分析。

[1]宋子齐等.视电阻率测井资料环境影响校正[J].测井技术，1995，9（4）：250-261.

[2]雍世和.最优化测井解释[M].山东：石油大学出版社，1995.134-136.

[3]陈宝林.最优化理论与算法[M].北京：清华大学出版社，2005.306-315.