长江江豚种群预测

长江江豚种群预测

刘毅恒

(西安交通大学数学与统计学院，陕西西安 710049)

摘要对长江江豚的生长现状进行了分析，采用改进的莱斯利模型对未来几年长江江豚的数量进行了预测，并用席勒模型对长江江豚的死亡率进行了估计。

关键词莱斯利模型；Siler模型；出生率；量化人类活动

中图分类号S937

作者简介刘毅恒(1993- )，男，安徽合肥人，从事生物建模方面的研究。

收稿日期2015-06-05

Population Forecast of Yangtze Finless Porpoise

LIU Yi-heng(School of Mathematics and Statistics, Xi'an Jiaotong University, Xi'an, Shaanxi 710049)

AbstractThe growth status of Yangtze finless porpoise was analyzed, the improved Leslie Model was adopted to estimate the quantity of Yangtze finless porpoise in the future, and the Siler Model was used to predict the demographic rate of Yangtze finless porpoise.

Key wordsLeslie Model; Siler Model; Demographic rate; Quantify human activity

长江江豚近年来在我国引发关于生态的讨论热潮。2006年，约40位科学家汇集一堂，寻找长江江豚的踪迹，却一无所获。2007年，长江江豚成为长江中唯一的豚类动物。作为窄脊豚类的子类，长江江豚主要分布于长江中下游。因其可爱的外形而被称为“扬子江仙子”。然而，调查发现长江江豚的数量正急剧减少，栖息地减少导致连续种群的断代，普遍的多样性降低，未来的某一天长江江豚有可能会走向灭绝。

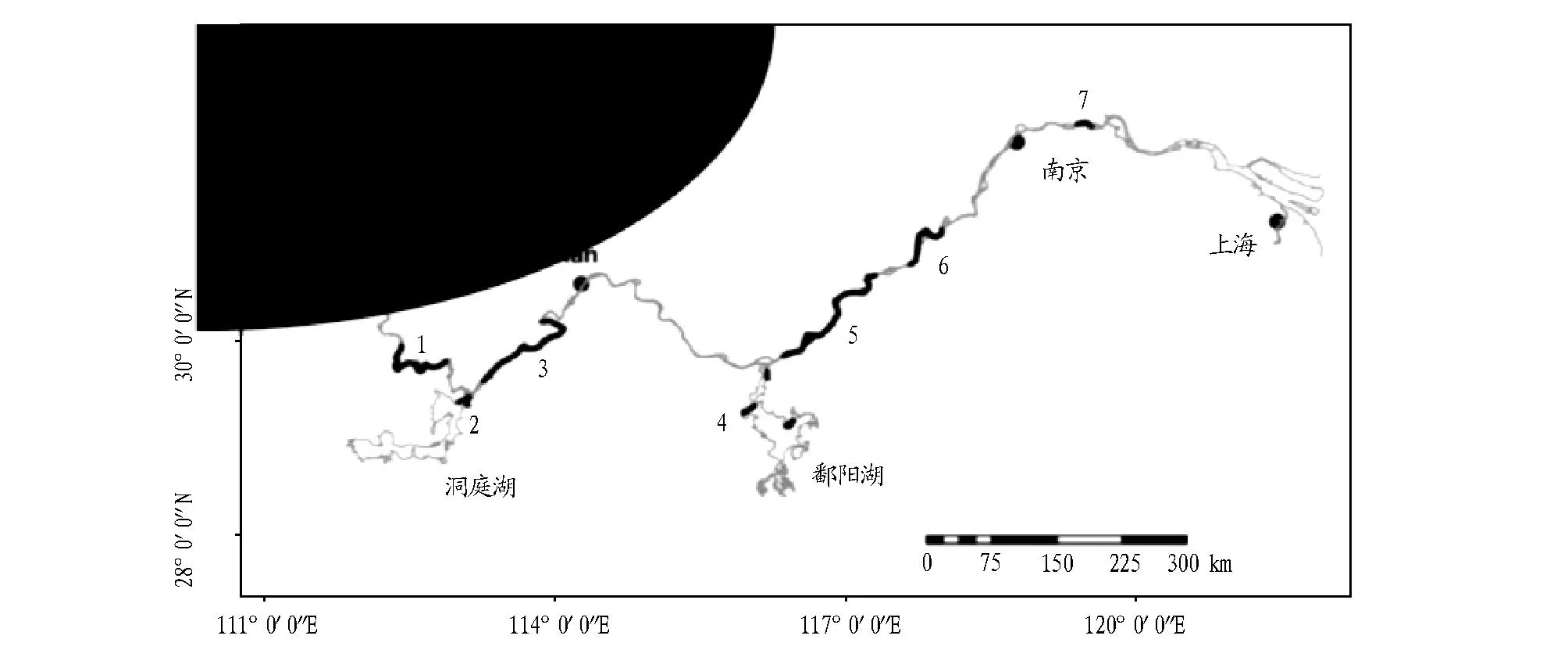
图1　长江江豚样本的采集地点

众所周知，江豚的唯一栖息地是我国中部的“黄金水渠”。这片地带生活着数以百万依赖农业、水产业和工业的人们，不幸的是货船来往的噪音、非法捕鱼以及“三峡大坝”之类的水利工程都对江豚的生存构成了巨大的威胁。长江江豚的数量1991年还有超过2 550只，2006年长江江豚数量已不到1 225只，江豚的数量大幅下降。为了解长江江豚的生存现状以及江豚数量的减少的实际速度，笔者建立了一个数学模型，并尝试对人类活动进行量化，研究人类活动对长江江豚数量的影响，并预测其种群变化。

1材料与方法

1.1样本采集长江江豚的采集地点如图1所示。

1.2方法

1.2.1莱斯利模型。长江江豚的繁殖数量随着个体年龄的不同而变化很大，使用莱斯利模型作为研究的主要框架，因为莱斯利模型[1]在处理这类问题时有着出色的表现。比如，2个相同规模的不同人类种群，1个群体年龄主要是20岁，另1个群体年龄主要是50岁，不同种群增长速度不同。年龄结构是很重要的。人类在具有生殖能力前要经历很长的时间，在性成熟后特定时代的不同社会因素或鼓励或抑制新生儿的出现，最终还有年长女性的绝经限制了繁殖。

为了获取这些因素对种群增速的影响，通过建立5个年龄分层的人类模型进行分析：x1(t)=时间t时刻，年龄在0～14岁的个体数量；x2(t)=时间t时刻，年龄在15～29岁的个体数量；x3(t)=时间t时刻，年龄在30～44岁的个体数量；x4(t)=时间t时刻，年龄在45～59岁的个体数量；x5(t)=时间t时刻，年龄在60～75岁的个体数量。

此外，可以额外设1个超过75岁的年龄阶层，当然也可以直接假设没有人能超过75岁。使用15年作为时间跨度，可以建立以下方程：

x1(t+1)= f1x1(t)+ f2x2(t)+ f3x3(t)+ f4x4(t)+ f5x5(t)

x2(t+1)=τ1,2x1(t)

x3(t+1)=τ2,3x2(t)

x4(t+1)=τ3,4x3(t)

x5(t+1)=τ4,5x4(t)

式中，fi代表第i年龄阶层的父母15年的生育率，τi,i+1代表第i个阶层的人能成功活到第i+1个阶层的生存率。由于1对父母可能在不同的年龄的分层，处理时将它们的子女分一半分别分到不同的组中。

利用矩阵表示，xt+1=Pxt，其中xt=(x1(t)，x2(t)，x3(t)，x4(t)，x5(t))是子群在时刻t的列向量，且

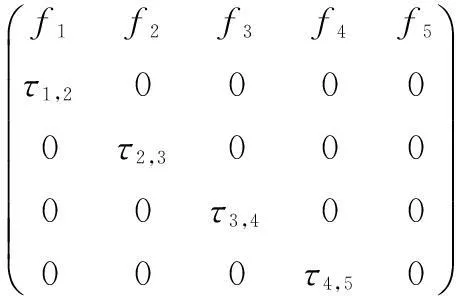
在长江江豚种群中，繁殖量随着年龄变化而变化，所以莱斯利模型很适合研究这个问题。

然而，在进行下一步前需要解决不够精确的问题。使用的所有死亡年龄数据(共279个江豚)都来自于长江中下游搁浅的随机收集。此外，由于只有身体长度和性别数据，通过查阅文献中江豚的特征，张先锋[2]使用68个江豚的有关数据推断出一个年龄跨度曲线。江豚的年龄X和身体长度(男性用Lm表示，女性用Lf表示)的关系由以下公式表示：

Lm=114.445 8x0.141 0

Lf=116.251 9x0.094 7

由此，可以得到数据样本的精确年龄分布(表1)。

1.2.2死亡率：席勒模型。使用莱斯利模型关系的另一个问题是江豚的生存率(死亡率)。由于关于生存率的历史数据差异很大，因此无法直接应用这些历史数据参数。运用席勒的生存的竞争风险模型[6]来估算江豚的生存率。使用席勒的1模型是因为它曾经准确描述了哺乳动物的生存和死亡率[7-8]。

表1　长江江豚的生命参数

在席勒的模型中，特定年龄的生存率l(x)由3个部分组成：

l(x)=lj(x)×lc(x)×ls(x)

由于青年导致的指数增长的风险因素：

所有年龄段共同拥有的常数风险:lc(x)=exp(-a2×x)

席勒的5个参数(风险系数：a1、a2、a3;调整参数：b1、b3)通过极大似然估计获得。

为了获得5个参数a1、a2、a3、b1、b3,需要使用极大似然估计。L(n) 是极大似然函数。

在莱斯利模型中，可以用下式表达:

τi,i+1=l(xi)=lj(xi)×lc(xi)×ls(xi)

1.2.3出生率。从样本中得到的出生率是莱斯利模型中的另一个重要因素。但是，考虑到现有的出生率模型的复杂度和知识工具的限制，很难直接计算江豚的出生率。在网上参阅了一些相关文献后发现，根据生物学信息可知无鳍豚类在每年的10月繁殖，一胎一个。因此，可以简单估计每个雌性江豚每年只有一个后代。因为还有很多其他因素在影响着江豚的出生率(如环境变化、气候、人类活动等)。假定新生江豚对雌性江豚的比例必须小于1。基于最初的目的是测算江豚将在几年内灭绝，所以，即使假设该比例就是1，仍然能看到江豚灭绝的高概率。

表2　长江江豚的各项基本参数

由表3可知，江豚的相对年龄是雄性4.5岁，雌性4岁。研究表明，江豚遵循一夫一妻制，一年只会生育一个后代。据此推测，每对年龄在4～16岁的江豚一年生育一个后代，表达为：

xi(t)按上文提到的定义;xm,i为长江中年龄为i的雄性江豚数量；xf,i为长江中年龄为i的雌性江豚数量。

1.2.4断层：人类影响的量化。在实际数据中，存在着一些数量上的“断层”，尝试找出其中的原因。

众多周知，人类活动对江豚种群的影响不容忽视，尤其是随着经济的发展，人们对江豚栖息地的破坏越来越大，因此将断层的存在解释为逐渐增加的人类活动的破坏，尤其是在经济发展的过程中。这是因为经济改革政策往往伴随着大规模的环境发展项目，比如大坝建设和土地开垦。

使用2002年的计算结果和2002年(1993年和2014年的中间年份)实际数据间的断层，来量化人类活动的影响程度。要将断层统一地运用到所有年龄层，就是假设各个年龄层的断层都等于总的年龄层断层。可用下式表达：

经改进，莱斯利模型确定为：

表4　各年龄长江江豚的生命参数 [7-8]

2结果与分析

从图2～4可以看出，考虑到人类活动的影响，预测的江豚灭绝时间接近20年。然而，没有控制的人类影响只会随着时间而加重，即使出生率为1。因而，江豚灭绝时间可能更早。

图2　不同性别各年龄长江江豚的数量

图3　各年龄长江江豚的总数

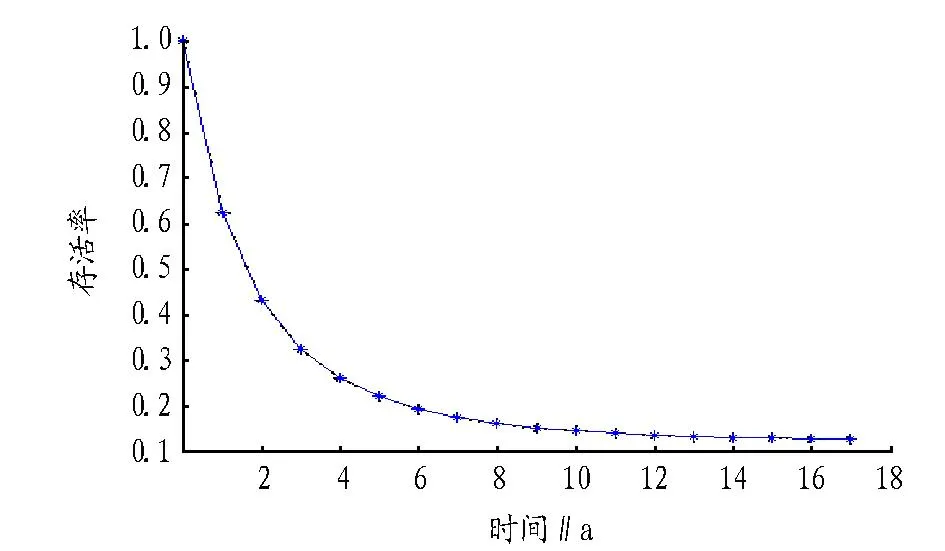
图4　长江江豚的灭绝时间预测

3讨论

3.1样本年龄分布的不确定性使用的所有死亡年龄数据都来自搁浅的江豚，这些数据是随机得在长江中下游搜集而来。因此，很难得到准确的年龄分布，通过查阅历史文献中关于无鳍江豚的身体特征的描述。张先锋[2]使用了68个样本的生物数据(包括性别和身体长度)导出年龄-长度曲线。江豚的年龄X和身体长度(男性用Lm表示，女性用Lf表示)的关系可用公式表示。因此，笔者使用上述的方程来估计213个江豚的年龄。

3.2关于无鳍江豚的生存率(死亡率)的不确定性对于莱斯利模型而言，江豚的生存率是很重要的。由于关于生存率的历史数据差异很大，无法直接应用这些历史数据参数。运用席勒的生存的竞争风险模型[6]来估算江豚的生存率。使用席勒的1模型是因为它曾经准确描述了哺乳动物的生存和死亡率。

3.3出生率由模型导出的出生率是莱斯利模型中的另一个重要因素。但是，考虑到现有的出生率模型的复杂度和知识工具的限制，很难直接计算江豚的出生率。在参阅了一些相关文献后发现，根据生物学信息可知，无鳍豚类在每年的10月繁殖，一胎一个。因此，可以简单估计每个雌性江豚每年只有一个后代。因为还有很多其他因素在影响着江豚的出生率(如环境变化、气候、人类活动等)。假定新生江豚对雌性江豚的比例必须小于1。并且，基于最初的目的是测算江豚将在几年内灭绝，所以即使假设该比例就是1，仍然能看到江豚灭绝是十分快速的。

3.4考虑人类活动的影响人类活动的对无鳍豚类的影响是不容忽视的，尤其是随着经济的发展，人们对江豚栖息地的破坏越来越严重。查阅其他人关于无鳍豚类种群的研究时发现，很少有人将人类活动影响当作一个很重要的因素。为了估计这个影响，使用了模型得出的结果，用于和历史实际数据对比(每4年的差值数据)得到了二者之间的断层。改革开放以来，长江沿岸的经济和工业活动呈指数型增长，同时还伴随着大规模的环境发展工程，比如兴修水坝和开垦土地。系统的大规模长江无鳍豚类的估计从1993年才开始发布。因此，舍弃了1993年前的数据，只关注1993～2012年的数据。2002年(1993年和2014年的中间年份)计算的断层，将其作为人类影响的量化程度的常值。

江豚种群的迅速减少是快速的工业和经济发展速度带来的结果，揭示了无节制的人类活动对水生鲸类动物的威胁。

3.5Matlab中遇到的问题当笔者尝试为席勒模型中的5个参数寻找极大似然解时发现，最终的结果将伴随着最初向量而变化。找到了几个可能的原因，其中最令人信服的却因为函数过于复杂，Matlab无法找到准确解。为了验证这个假设，使用gatbx工具来解决问题，最终的结果显示解是局部最小值。某种程度上，它证明了笔者的猜想，但无法完全确定这2个结果之间的联系。

参考文献

[1] MEI Z G，HUANG S L，HAO Y J，et al.Accelarating population decline of Yangtze finless porpoise[J].Biological Conservation，2012，153:192-200.

[2] 张先锋.江豚的年龄鉴定、生长和生殖研究[J].水生生物学报，1992(4):289-298.

[3] GAO A, ZHOU K Y. Growth and reproduction of three populations of finless porpoise [J].Aquat Mammals, 1993, 19:3-12.

[4] HAO Y J,CHEN D Q,ZHAO Q Z,et al.Serum concentrations of gonadotropins and steroid hormones ofNeophocaenaphocaenoidesasiaeorientalisin middle and lower region of the Yangtze River[J].Theriogenology, 2007, 67:673-680.

[5] ZHANG X F,WANG K X.Population viability analysis for the Yangtze finless porpoise[J].Acta Ecologica Sinica, 1999, 19: 529-533.

[6] SILER W.A competing risk model for animal mortality[J].Ecology，1979，60:750-757.

[7] BARLOW J，BOVEN P.Modeling age-specific mortality for marine mammal populations[J].Mar Mammal Sci,1991，7(1):56-65.

[8] STOLEN M K,BARLOW J.A model life table for bottlenose dolphins(Tursoipstruncatus) from the Indian River laggon system，Florida，USA[J].Mar Mammal Sci，2003，19(4):630-649.