双基线极化干涉SAR植被参数反演

卢红喜,李东霖,刘宏伟,索志勇,宋文青,保 铮

(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071；2.上海卫星工程研究所,上海 200240)

双基线极化干涉SAR植被参数反演

卢红喜1,李东霖2,刘宏伟1,索志勇1,宋文青1,保 铮1

(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071；2.上海卫星工程研究所,上海 200240)

植被参数反演是极化干涉合成孔径雷达的重要应用,然而单基线极化干涉合成孔径雷达技术无法解决体散射去相干估计的模糊问题.提出了一种新的双基线极化干涉合成孔径雷达技术,充分利用了双基线观测数据的相关性,能够有效地解决体散射去相干估计的模糊问题,并对基线比例较小的情况仍具有较好的鲁棒性.利用欧空局发布的PolSARPro软件仿真验证了该方法的有效性和稳健性.

极化干涉合成孔径雷达;植被参数反演;双基线解模糊;聚类分析

极化干涉合成孔径雷达（Polarimetric Synthetic Aperture Radar interferometry,PolInSAR)因其对散射体材质、形状、方向和空间分布极为敏感,在植被覆盖区地形干涉相位获取、植被参数估计（如森林高度、植被体衰减系数等)和森林分类与制图等应用领域表现出巨大的优势[1-4].然而,实际观测自然场景的地体散射幅度比仅存在于一个较小的范围,单基线极化干涉合成孔径雷达技术无法准确地获取仅含有体散射相干系数的极化通道,因而体散射分量的估计存在严重的模糊问题,极大地影响了植被参数估计的可靠性.目前,利用双基线极化干涉合成孔径雷达技术进行植被参数反演的主要算法包括双基线鲁棒参数反演方法[5]、双基线联合优化模型类求解法[6-7]、基于RMoG模型的双基线内点法[8]等.其中双基线鲁棒参数反演方法受限于长短基线的长度比例,无法应用于长短基线比例较小的情况;联合优化模型类求解法主要受限于初始值的选择,并且无法收敛到全局最优解;基于RMoG模型的双基线内点法同样基于最优化方法,虽然可以估计植被的高度,但对植被衰减系数的估计仍然存在模糊甚至解不惟一的问题.针对这些问题,笔者首先给出了存在距离向地形坡度的S-RVoG植被参数反演模型,分析了双基线极化干涉合成孔径雷达信号模型及其几何对应关系,在此基础上详细阐述并论证了双基线极化干涉合成孔径雷达技术解体散射去相干模糊的基本原理,同时还对该方法进行了定量的误差分析与评估.

1 植被参数反演模型

森林植被散射一般被建模为由地面散射和植被体散射（Random Volumeover Ground,RVoG)构成的两层散射模型[9].在文献[9]中,RVoG模型假设植被层散射体导向随机、均匀分布,植被层衰减系数为常数,且入射波呈指数衰减;入射波在地质层穿透深度为零,在临界处发生面散射,散射回波强度与极化方式相关.然而,这一模型并未考虑植被区地形的起伏变化,而其对植被散射及参数反演精度的影响极为显著[10].实际上,距离向地形起伏对两层散射模型假设的影响主要反映在垂直波数的变化上,如图1所示.

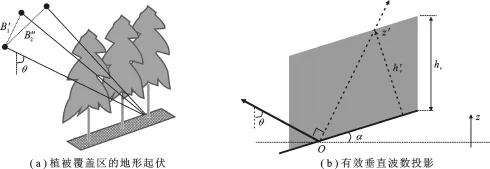
图1 考虑地形起伏的植被覆盖区S-RVoG散射模型

对于实际干涉基线长度为B′1和B″2的双基线极化干涉合成孔径雷达系统,如图1所示,干涉合成孔径雷达（Synthetic Aperture Radar,SAR)有效垂直波数[9]沿距离向地形坡面法线的投影,即沿z′方向等效的干涉有效波数可表示为

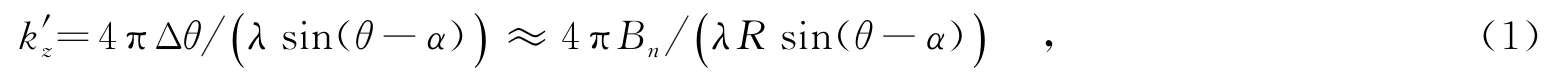
其中,λ为波长,θ为主天线雷达视角,Bn（n=1,2)为相应的有效基线长度,Δθ为基线Bn对目标分辨单元形成的视角差,R为雷达与目标的距离,α为地形距离向坡度.相应地,高度为hv的植被层沿z′方向的等效高度h′v=hvcosα.

因此,对于存在距离向地形起伏的情况,可沿如图1（b)所示的z′方向对地表及植被两层散射过程进行积分,完成极化干涉观测信号的建模,即采用S-RVoG植被参数反演模型[11],可表述为

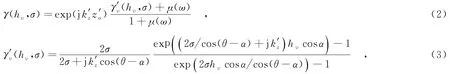
其中,σ为植被衰减系数,z′o为当前分辨单元地形坡面沿z′方向的高程.实数μ（ω)表示地面散射与体散射幅度之比,其取值随着观测极化方式ω变化,且μ（ω)∈（0,+∞).

由于S-RVoG模型在z′坐标系统下等效于传统的RVoG模型,因此经典的三阶段方法[12]仍然适用.根据最终估计得到的体散射相干系数v,结合式（3)并利用查表法（Look-Up Table,LUT)即可计算得到地形起伏区域的植被参数（v).需要说明的是,在模型式（3)中,地形坡度参数α可通过迭代的S-RVoG模型反演方法[11]进行估计.

2 双基线极化干涉解模糊算法原理

首先简要介绍双基线极化干涉合成孔径雷达信号模型,再在此基础上给出利用双基线极化干涉合成孔径雷达数据进行体散射去相干解模糊的算法流程与算法性能分析.

2.1 双基线极化干涉合成孔径雷达信号模型

在单基线极化干涉合成孔径雷达系统中,主辅雷达以近似相同的视角分别获取全极化散射向量k1、k2,则相应的极化相干矩阵可表示为

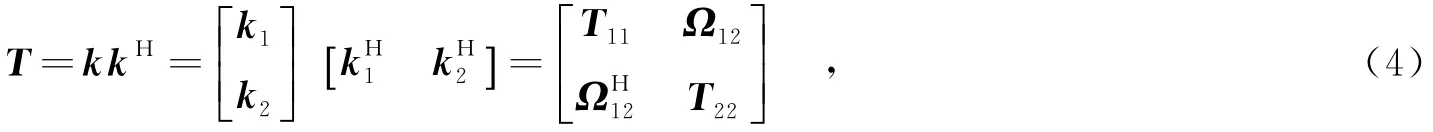
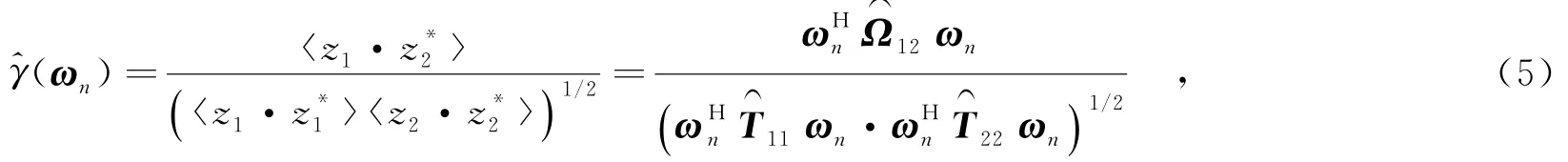
根据式（2)给出的极化干涉植被散射模型,去除地形干涉相位后的极化干涉合成孔径雷达复相干系数可表示为

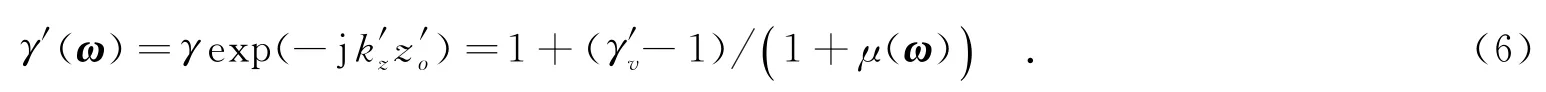
随着观测极化方式ω的变化,当μ（ω)由0增大到+∞时,γ′（ω)在复平面单位圆内将沿直线由点γ′v移动至点（1,0)（即地面散射相对参考点O).

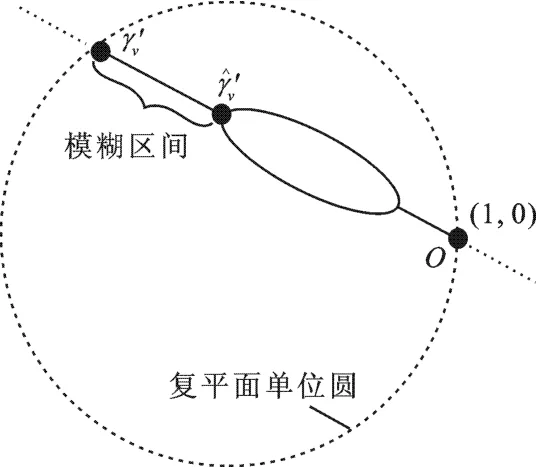
图2 体散射相干系数模糊区间

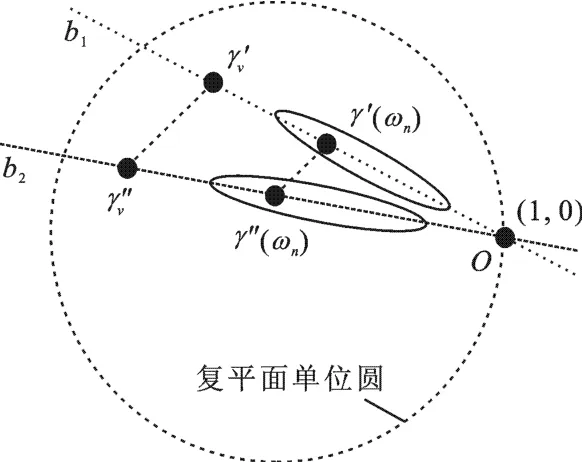
图3 基于双基线极化干涉的体散射去相干解模糊

经典三阶段法的基本思想就是利用这一线性性质,即选取大量的极化方式ωn,在复平面上对式（5)计算得到的复相干系数进行直线拟合,并选取最小地体散射幅度比的极化通道作为体散射复相干系数的估计值′v,最后再利用查表法求解植被参数,如图2所示.然而,随着极化方式的改变,实际自然场景的地体散射幅度比仅存在于一个较小的范围,即μ（ω)无法取遍（0,+∞)整个区间.根据表达式（6),对于任意给定的观测极化方式ωn,可以计算得到地体散射幅度比为

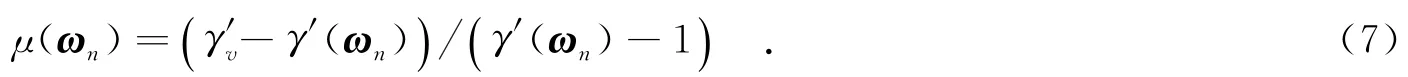
针对单基线极化干涉体散射去相干的模糊问题,一种可行的考虑是额外增加一根观测基线进行测量.对于有效基线长度分别为B1和B2的双基线极化干涉系统,其获取的观测数据可分别进行处理,即按照式（5)计算得到复相干系数散布区域,进而估计各散布区域线性变化的主导方向,得到复相干系数散布的直线模型.在去除相应的地形干涉相位后,基线B1和B2对应的线性方程b1、b2相交于地面散射相对参考点O,其观测得到的体散射相干系数γ′v和γ″v也分别位于直线b1、b2上,如图3所示.根据γ′v和γ″v在复平面内的相对位置关系,即可解决体散射复相干系数估计的模糊问题.下面给出其理论依据及相应的算法流程和性能分析.

2.2 双基线解模糊算法流程

由于地体散射幅度比μ衡量的是植被区散射体的固有散射属性,对于视角近似相同的双基线极化干涉合成孔径雷达系统而言,同一分辨单元的植被区散射体应具有一致的地体散射幅度比.因此,对于如图3所示的B1、B2双基线几何模型,根据式（7)可得到如下关系:

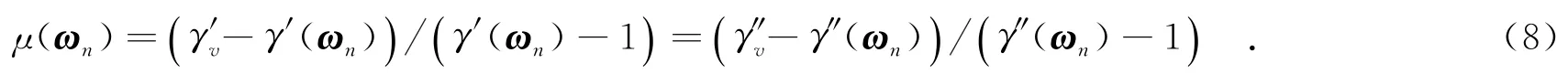
在上述几何性质的基础上,针对双基线极化干涉合成孔径雷达植被参数反演问题,笔者首先给出双基线解模糊算法的基本流程:

（1)双基线极化干涉复相干系数分布模型构建.对两基线B1、B2获取的数据分别进行极化干涉合成孔径雷达处理[12],即选取大量的观测极化方式ωn（n=1,…,N),根据式（5)计算得到极化干涉合成孔径雷达复相干系数,分别拟合出相应的直线方程,并确定地面散射复相干系数,在分别校正地形干涉相位后得到′（ωn)和″（ωn),以及如图3所示相交于O点的直线b1、b2.

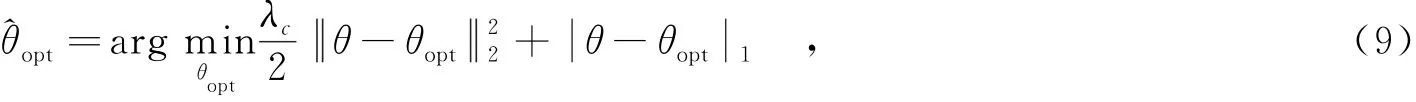
其中,λc∈[0,+∞),为目标函数影响比例因子;观测样本θ=[θ1,θ2,…,θn,…,θN]T.

（4)双基线植被参数查表法反演.基于式（3)的结果,采用查表法,由′v、″v分别计算出参数（σ,hv)的两组候选估计值′′v)、（″,″v).

（5)最大一致性参数选取.根据两基线B1、B2分别得到的植被参数在理论上应该是一致的,并且这个理论值存在于点γ′v、γ″v处.因此可以对（′,′v)、（″,″v)这两组参数估计值之间的一致性进行判定,当且仅当直线l经过点γ′v、γ″v时其一致性达到最大,l在该位置得到的交点即为体散射复相干系数的最优估计值.在此,归一化的不一致性判定准则可定义为

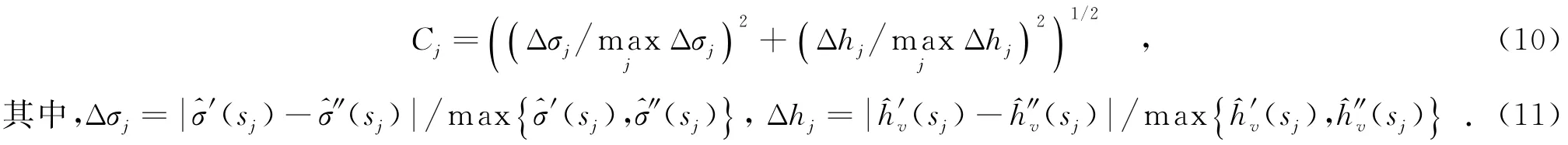
上式中,sj为直线l由O点向单位圆内平行移动时沿直线b1的相对位置（即其移动距离与直线b1为单位圆所截线段长度的比值).基于这一准则,最优的植被参数估计值可表示为

2.3 算法性能分析

下面分别描述两个仿真试验,作为对倾角估计聚类算法及最大一致性判定准则的补充说明,并给出算法的性能分析及误差分析.需要说明的是,由于RVoG模型的有效性已有大量的文献进行了分析与论证[1,15-16],这也是笔者的基本假设前提,因此对此将不再赘述.

（1)聚类算法仿真分析试验.为了验证该方法的有效性,图4给出了一组基于欧空局Pol SA Rpro双基线L波段极化干涉仿真数据的复相干系数分布情况.由图4可见,对于所给的3组不同μ（ω),倾角具有明显的同向趋势.为了进行定量分析,图5给出了由该数据计算得到的倾角θn统计直方图.分析图5可知,数据样本θn具有明显集中趋势的聚类现象,而直方图的峰值点对应为该数据的惟一众数[17].众数为样本中出现概率最大的样本值,而样本均值对应为最小二乘意义上的概率统计值.因此,从本质上来说,式（9)目标函数中的l1范数与l2范数混合准则是对众数与均值的折中,而比例因子λc依赖于具体试验数据.对于这一类集中趋势极为明显的样本数据,实际中可选取经验值λc=0.01.

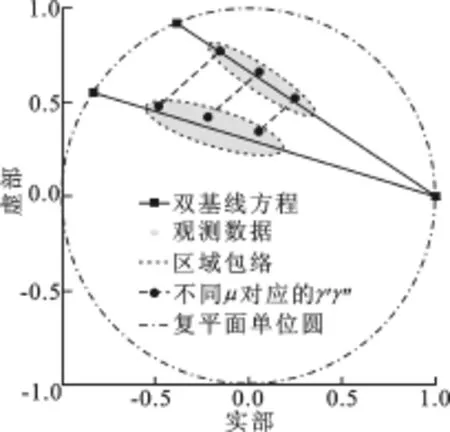
图4 仿真数据中不同μ(ω)对应的线段

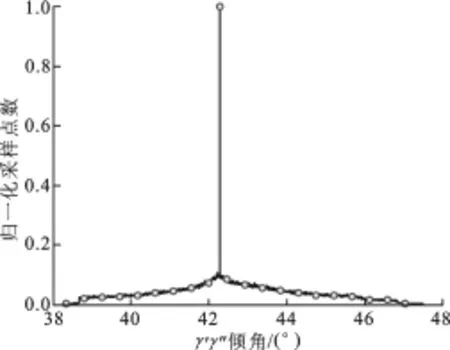
图5 仿真数据中不同μ(ω)对应的倾角统计直方图

（2)最大一致性准则仿真分析试验.下面通过仿真试验对不一致性判定准则式（10)的有效性进行验证.在仿真试验中,首先给定雷达系统平台、地表层和植被层基本参数,如表1所示.根据式（3)分别计算双基线B1、B2极化干涉系统观测下的体散射复相干系数理论值γ′v、γ″v,则直线b1、b2由O点与γ′v、γ″v之间的连线惟一确定.定义基线比例ρ=B2B1,根据表1所给参数,分别仿真了ρ=1.1,ρ=2.0和ρ=5.0这3种情况.依照上述双基线解模糊算法流程步骤（3)～（5),计算得到候选估计值间的不一致性参数变化曲线C,其结果如图6所示.仿真试验结果表明,当且仅当σ=0.06 d B/m,hv=13 m时（即s=0.835处),不同基线比例情况下的不一致性参数均取得最小值（Cmin=0),如图6所示.由此可见,基于上述双基线几何对应关系,采用不一致性判定准则可以有效地解决体散射复相干系数的模糊问题.此外,随着基线比例的增大,不一致性参数曲线C在极值点的锐化程度也愈明显,而基线比例较小的情况则并不明显,图6的分析结果在文献[5]中也得到了相应的印证.

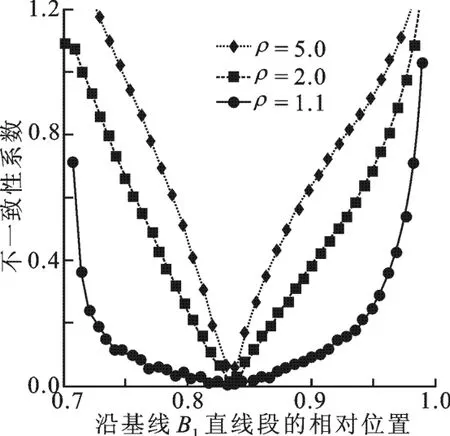
图6 不一致性准则有效性分析仿真验证结果

表1 平台及场景仿真参数

（3)聚类中心估计误差对一致性判定准则的影响分析.当聚类算法所得的聚类中心存在误差时,由不一致性准则式（10)最小化求解得到的植被参数反演精度也必然受到影响.为了定量评估聚类中心估计误差的影响,针对表1所示的仿真参数,分析了不同的误差扰动量对参数估计算法性能的影响,结果如图7和图8所示.由图7可知,当且仅当倾角误差为零时,不一致性参数曲线C取得最小值（Cmin=0);当倾角的估计值存在误差时,Cmin＞0,并且随着误差的增加,Cmin有增大趋势.此外,随着基线比例的减小,倾角误差在相同情况下,Cmin有明显的增大趋势,由Cmin反演得到的植被参数估计误差也就增大.由此可见,基线比例越小,则直线b1、b2的夹角越小,相应的双基线系统进行植被参数反演时对误差的鲁棒性也就越差.更为直观地,图8给出了ρ=1.1时聚类中心估计误差对植被参数反演的影响分析曲线,可见即使3°的倾角估计偏差也将引入较大的参数估计误差,其中植被高度hv估计误差最高可达9%,衰减系数σ估计误差最高可达1%.需要说明的是,由于最终的植被参数估计结果由不一致性判定准则的定义方式、倾角及其误差影响共同决定,因而图8中的误差曲线在一定范围内会呈现出随倾角误差上下波动的情况.

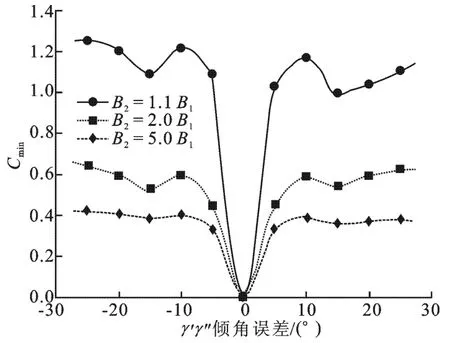
图7 聚类中心偏差对参数C影响的分析曲线

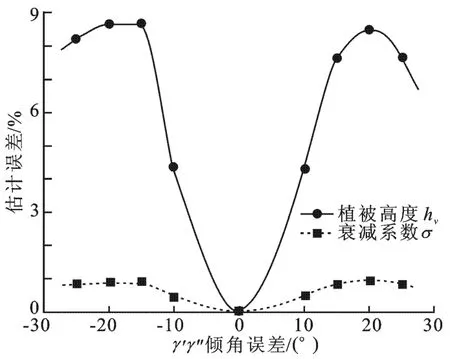
图8 ρ=1.1时聚类中心偏差对参数反演精度影响的分析曲线

3 仿真试验结果

利用欧空局提供的L波段森林植被的极化干涉合成孔径雷达仿真数据验证了笔者提出的双基线聚类分析植被反演算法的性能.实验中利用欧空局研发的PolSARPro软件获取了双基线B1=10 m、B2=13.4 m系统采集的自然场景极化干涉合成孔径雷达数据,主要的仿真场景参数和雷达几何参数如表2

表2 试验仿真参数

表3 试验处理结果对比

所示.为了与现有的极化干涉合成孔径雷达植被参数反演算法进行对比,分别采用单基线经典三阶段法[11-12]、双基线联合优化模型方法和笔者提出的双基线聚类分析植被反演算法对该组数据进行处理,统计数据结果如表3所示.图9给出了传统单基线方法与笔者提出的植被参数反演方法估计结果的统计直方图.

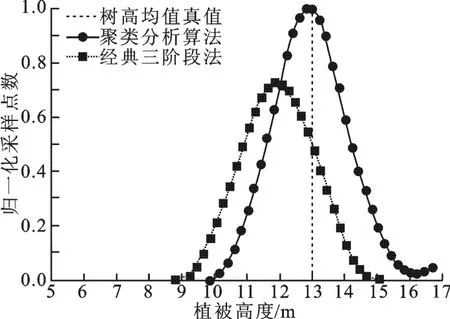
图9 ρ=1.1时聚类中心偏差对参数反演精度影响分析曲线

单基线经典三阶段法由于无法解决体散射去相干的模糊问题,其估计结果存在一定程度的偏低,如图9和表3的试验处理结果所示.此外,本试验中联合优化方法的估计结果与单基线经典三阶段方法估计的树高均值结果相当,但由于寻优过程收敛结果受初始值选择的影响,该方法的估计误差和均方根误差较大.从表3可以看出,基于聚类分析的双基线极化干涉合成孔径雷达植被参数反演方法可以准确地估计出植被参数,其参数估计的树高均值、误差以及均方根误差指标均优于单基线经典三阶段方法和双基线联合优化方法.

4 总 结

针对单基线植被参数反演应用中的体散射去相干模糊问题,笔者提出了一种基于聚类分析的双基线极化干涉合成孔径雷达植被参数反演方法.该方法首先对原始观测数据分别进行处理,构建双基线极化干涉复相干系数分布模型;考虑到双基线极化干涉观测数据的内在关联性,提出了基于聚类分析方法的体散射复相干系数对倾角估计算法;最后,根据文中定义的最大一致性准则对体散射复相干系数对在复平面内的位置进行准确估计,并采用查表法准确地获取植被参数.仿真试验分析结果以及试验数据处理结果表明,笔者提出的算法能够有效地估计体散射复相干系数对的位置,避免了单基线对体散射去相干求解的模糊问题,从而保证了植被参数的估计精度.

[1]López-Martínez C,Alonso-González A.Assessment and Estimation of the RVoG Model in Polarimetric SAR Interferometry[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(6):3091-3106.

[2]Arnaubec A,Roueff A,Dubois-Fernandez P C,et al.Vegetation Height Estimation Precision With Compact PolInSAR and Homogeneous Random Volume Over Ground Model[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(3):1879-1891.

[3]de Castro-Filho C A P,da Costa Freitas C,Siqueira Sant’Anna S J,et al.Relating Amazon forest biomass to PolInSAR extracted features[C]//International Geoscience and Remote Sensing Symposium.Piscataway:IEEE,2013:957-960.

[4] 秦华,周沫,察豪,等.软件雷达信号处理的多GPU并行技术[J].西安电子科技大学学报,2013,40(3):145-151. Qin Hua,Zhou Mo,Cha Hao,et al.Research on Multi-GPU parallel Technology in Software Radar Signal Processing [J].Journal of Xidian University,2013,40(3):145-151.

[5]Cloude S R.Robust Parameter Estimation Using Dual Baseline Polarimetric SAR Interferometry[C]//International Geoscience and Remote Sensing Symposium.Piscataway:IEEE,2002:838-840.

[6] 陈曦,张红,王超.双基线极化干涉合成孔径雷达的植被参数提取[J].电子与信息学报,2008,30(12):2858-2861. Chen Xi,Zhang Hong,Wang Chao.Vegetation Parameter Extraction Using Dual Baseline Polarimetric SAR Interferometry Data[J].Journal of Electronics&Information Technology,2008,30(12):2858-2861.

[7]Cloude S R,Williams M L.A Coherent EM Scattering Model for Dual Baseline POLInSAR[C]//International Geoscience and Remote Sensing Symposium.Piscataway:IEEE,2003:1423-1425.

[8]Lavalle M,Khun K.Three-baseline InSAR Estimation of Forest Height[J].IEEE Geoscience and Remote Sensing Letters,2014,11(10):1737-1741.

[9]Papathanassiou K P,Cloude S R.Single-baseline Polarimetric SAR Interferometry[J].IEEE Transactions on Geoscience and Remote Sensing,2001,39(11):2352-2363.

[10]Lavalle M,Solimini D,Pottier E,et al.Forest Parameters Inversion Using Polarimetric and Interferometric SAR Data [C]//International Geoscience and Remote Sensing Symposium.Piscataway:IEEE,2009:129-132.

[11]Lu H X,Suo Z Y,Guo R,et al.S-RVoG Model for Forest Parameters Inversion over Underlying Topography[J]. Electronics Letters,2013,49(9):618-619.

[12]Cloude S R,Papathanassiou K P.Three-stage Inversion Process for Polarimetric SAR Interferometry[J].IEE Proceedings:Radar,Sonar and Navigation,2003,150(3):125-134.

[13]Tan L L,Yang R L.Investigation on Tree Height Retrieval with Polarimetric SAR Interferometry[C]//International Geoscience and Remote Sensing Symposium.Piscataway:IEEE,2008:546-549.

[14]Beck A,Teboulle M.A Fast Iterative Shrinkage-thresholding Algorithm for Linear Inverse Problems[J].SIAM Journal on Imaging Sciences,2009,2(1):183-202.

[15]López-Martínez C,Alonso A.A Study of the RVoG Coherent Scattering Model Validity in PolInSAR for Forests Studies[C]//International Geoscience and Remote Sensing Symposium.Piscataway:IEEE,2013:2349-2352.

[16]López-Martínez C,Fabregas X,Alonso-González A.Analysis and Validity of the PolInSAR Line Model on Forested Areas[C]//European Conference on Synthetic Aperture Radar.Piscataway:IEEE,2012:697-700.

[17]Bishop C M.Pattern Recognition and Machine Learning[M].Cambridge:Springer,2008:44-63.

（编辑:郭 华)

Forest parameters retrieval with dual-baseline polarimetric SAR interferometry based on clustering analysis

LU Hongxi1,LI Donglin2,LIU Hongwei1,SUO Zhiyong1,SONG Wenqing1,BAO Zheng1
(1.National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China; 2.Shanghai Institute of Satellite Engineering,Shanghai 200240,China)

Forest parameters inversion is an important application of Polarimetric Synthetic Aperture Radar Interferometry(PolInSAR).To resolve the volume decorrelation coefficient ambiguity of single-baseline PolInSAR,a new dual-baseline PolInSAR approach is proposed in this paper.The correlation of dual-baseline data is fully investigated to resolve the ambiguity problem effectively,and the performance of the proposed approach is proved to be of great robustness in a very small baseline ratio system.Finally,experimental results with ESA dual-baseline PolInSAR simulated data validate the effectiveness and robustness of the proposed approach.

polarimetric synthetic aperture radar interferometry;forest parameters inversion;dualbaseline volume ambiguity-resolving;clustering analysis

TN957

A

1001-2400（2015)06-0023-07

10.3969/j.issn.1001-2400.2015.06.005

2014-06-20

时间:2015-03-13

国家自然科学基金资助项目（61271024,61201292,61201283);全国优秀博士学位论文作者专项资金资助项目（FANEDD-201156);新世纪优秀人才支持计划资助项目（NCET-09-0630);中央高校基本科研业务费专项资金资助项目（K5051302014)

卢红喜（1987-),男,西安电子科技大学博士研究生,E-mail:xdkd@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.005.html