交流系统接地故障对直流换相的影响

尹广力，李干

(国网北京昌平供电公司，北京 102200)

交流系统接地故障对直流换相的影响

尹广力，李干

(国网北京昌平供电公司，北京 102200)

利用序分量法详细推导了交流系统发生不同接地故障时换相电压与线电压过零点偏移的变化情况，比较系统地分析了各种交流侧接地故障对换相失败的影响。分析结果表明：不同的故障类型对阀的换相过程影响不同；随着过渡电阻的变化，换相电压过零点偏移可能会从超前转为滞后；并基于理论分析结果对关断角的表达式进行了相应的修正。最后以国际大电网国际会议HVDC标准仿真模型，验证了结论的正确性；并利用仿真结果对影响换相失败的两大因素，即换相电压和过零点偏移的影响程度进行了探讨。

换相失败；序分量法；过渡电阻；换相电压；相位偏移

0 前言

换相失败是高压直流输电系统中最常见的故障之一，它将导致直流电压降低、输送功率减少、电流增大、换流阀寿命缩短、换流变压器直流偏磁及逆变侧弱交流系统过电压等不良后果[1]。若采取的控制措施不当，还会引发后继的换相失败，严重时将导致直流传输功率中断，使整个系统失去稳定，影响电网的安全运行[2-5]。引发直流输电系统换相失败的原因可分为2大类：第1类是直流输电系统自身的故障；第2类是受端交流系统故障或扰动。其中换相失败对交流系统的故障尤为敏感，交流侧故障是诱发换相失败的主要原因[6]。因此研究交流侧故障对换相失败的影响具有重大意义。

本文利用序分量法，充分考虑了实际短路故障中存在过渡电阻的因素，比较系统地分析了各种接地故障对换相失败的影响，并详细推导了交流系统故障时换相电压幅值和过零点偏移角度之间的关系，同时对关断角的表达式进行了相应的修正。最后基于EMTDC/PSCAD仿真模型验证了结论的正确性，并探讨了换相电压与过零点偏移对换相失败不同的影响程度。

1 换相失败的机理

当两个桥臂之间换相结束后，刚退出导通的阀在反向电压作用的一段时间内，如果未能恢复阻断能力或在反向电压期间换相过程一直未能进行完毕，这两种情况在阀电压转变为正向时，被换相的阀都将向原来预定退出导通的阀倒换相，即换相失败[1]。换相失败的根本原因是关断角γ过小[9]。当逆变侧交流系统发生不对称故障并使换相电压过零点前移角度φ时，逆变器关断角的表达式为[10]：

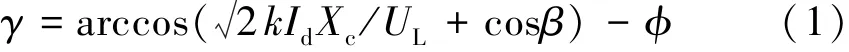
式中k为换流变压器的变比，Xc为换相电抗，UL为换流母线线电压有效值，β为越前触发角。显然，发生对称性故障时φ=0。

当γ＜γmin时表示直流系统发生换相失败。其中γmin对应换流阀恢复阻断能力所需的时间，考虑到串联元件的误差，一个可控硅阀的恢复时间γmin≈10°[8]。

2 交流侧接地故障对换相失败影响

交流侧故障对换相失败的影响主要体现在换相电压幅值变化和线电压过零点偏移 (不对称故障)两个方面，因此下面的分析主要围绕这两个方面展开。需要指出的是：HVDC输电系统一般采用12脉动换流器，为了便于分析，本文以Y型换流器为例，D型换流器的分析方法与此相同，不再赘述。

2.1 单相接地短路

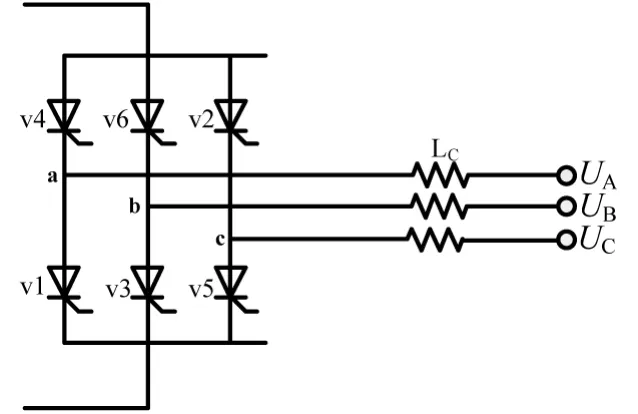
图1 三相桥式逆变器等效电路

则网侧的三相线电压表达式为：

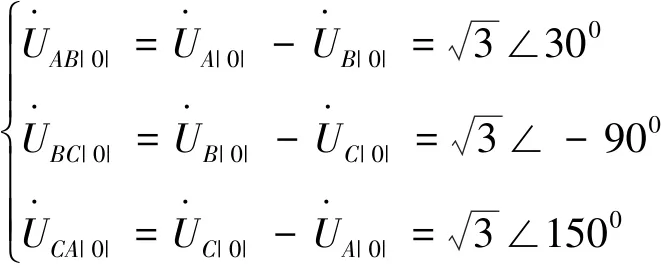
在直流系统没有出现换相失败的情况下，如果交流侧发生A相接地故障，那么由故障分析可知，短路点的各序电流、电压为：

将各序分量叠加后即可得到故障点处的ABC三相电压，而换相电压实际为换流变阀侧线电压，因此需分析故障前后阀侧线电压的变化情况。但注意到对于Y型换流变压器，假设变比为1，则原、副边的相电压幅值、相位均相同，因此仅需分析网侧的线电压变化情况即可。另外，通常假设电力系统的正负序阻抗近似相等，即x1∑=x2∑，由此得到的故障后网侧各个线电压如式 (5)：

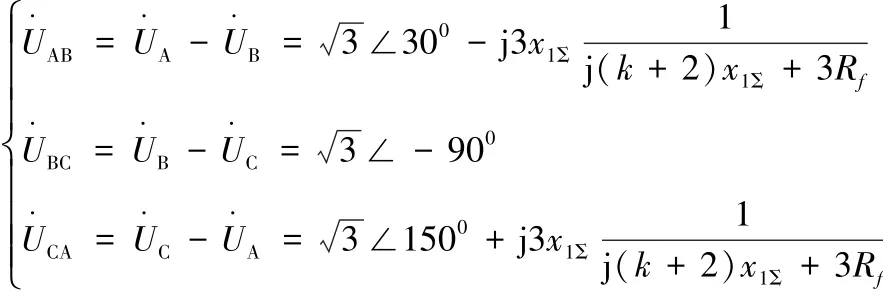
经推导对于形如1/(R+jx)的表达式，当x不变，R从0增大到∞时的轨迹是复平面上的半圆，直径为1/x。于是，由式 (5)可得AB的变化轨迹如图2所示，其中半圆的直径｜AD｜=

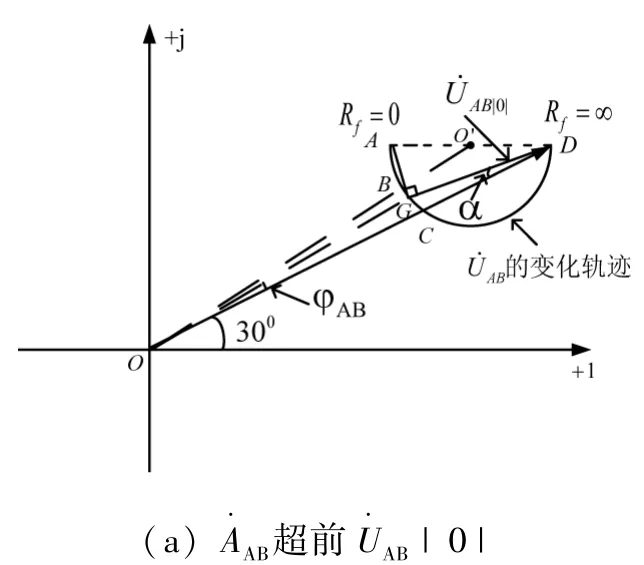
图2 AB的变化轨迹图

由图2可知：

1)随着Rf从0逐渐增大为∞，AB的相位从超前变化到滞后AB｜0｜，C为临界变化点，对应的过渡电阻，可称为中值电阻。

由上述分析可知，随着Rf的不断增加，AB将由超前变化为滞后于AB｜0｜，其偏移的角度φAB计算如下：

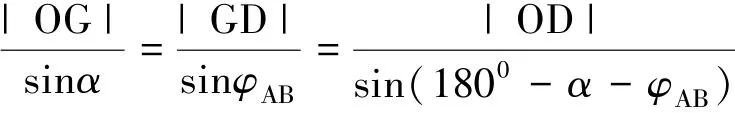
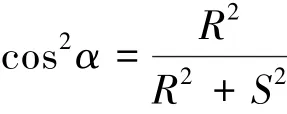
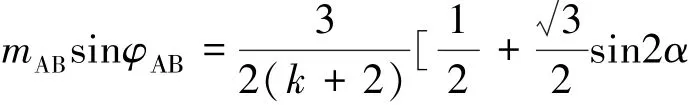
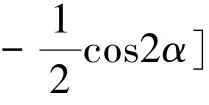
由式 (8)可得：

将其代入式 (9)中，即得：

式 (11)即为故障后的AB线电压超前时电压幅值与过零点偏移角度之间的关系。

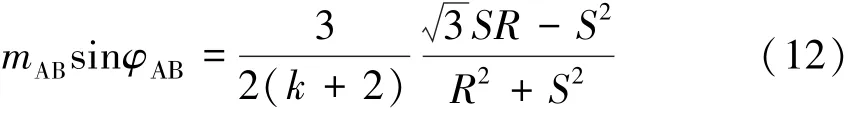
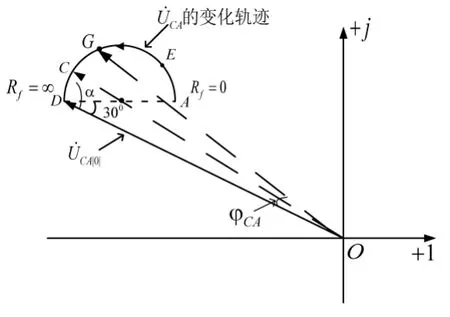
图3 CA的变化轨迹图

1)随着过渡电阻Rf从0增大到∞，CA的幅值mCA先增大后减小，即在弧AC上，mCA随着Rf的增大而增大，在弧CD上，mCA随着Rf的增大而减小，幅值最大值出现在C点。当k=3时，1.249≤mCA≤1.780。

设G为半圆上任一点，则｜OG｜=mCA，则CA相对CA｜0｜的相位偏移φCA与幅值的关系：

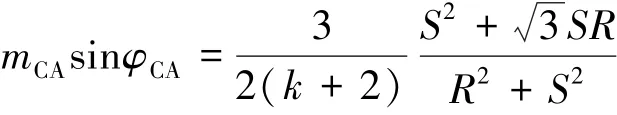
其中：R= 3-mCAcosφCA，S=mCAsinφCA。

表1给出了交流侧发生A相接地故障时，换相电压的幅值与过零点偏移角度之间的关系。

表1 A相接地故障时线电压幅值与相位偏移的关系

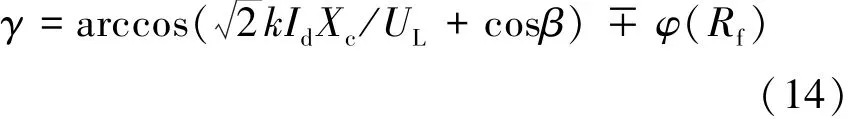
其中φ(Rf)表示线电压过零点偏移的角度是过渡电阻的函数，前移时取负号，后移时取正号。

3)随着过渡电阻的增大，三个线电压的幅值降落减小，过零点后移，由式 (14)可知γ增大，因而发生换相失败的可能性大为降低。

两相接地故障和三相接地故障分析过程与上述方法相同，限于篇幅，只给出相应的结论。

2.2 两相接地短路

由故障分析可得短路后的线电压为：

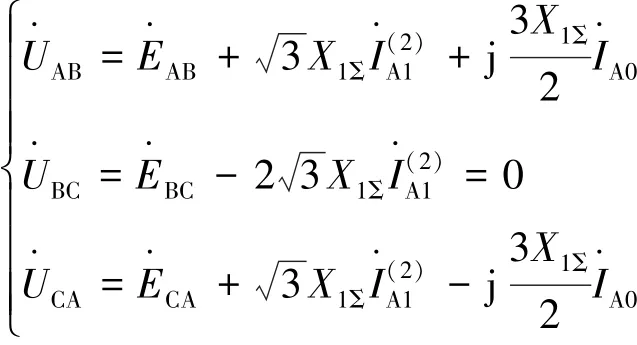
图4 两相故障时的线电压变化轨迹图

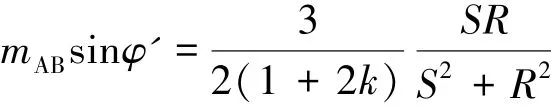
其中：R=1.5-mABcosφ′，S=mABsinφ′。

表2给出了BC两相接地故障时换相电压的幅值与相位偏移之间的关系。

表2 BC两相接地故障时换相电压的幅值与相位偏移的关系

2.3 三相接地短路

发生三相对称性故障时，换流母线处的各个线电压为：

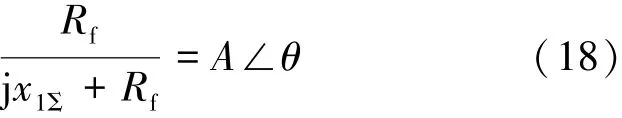
当Rf从0变化到∞时，0≤A≤1，-900＜θ≤0°。可见故障后每个线电压幅值都降低，过零点后移。因此理论上讲，三相短路时对每个阀的换相过程影响相同。

其中φφ表示AB、BC、CA。

由式 (17)可知，三相线电压在故障前后，幅值相位均有所变化，且变化幅度及趋势相同。不妨设

3 仿真验证

3.1 仿真模型

采用电磁暂态仿真软件PSCAD/EMTDC，基于国际大电网标准测试模型，搭建了如图4所示仿真模型。仿真模型采用单级运行方式，换流站采用12脉动换流器接线。

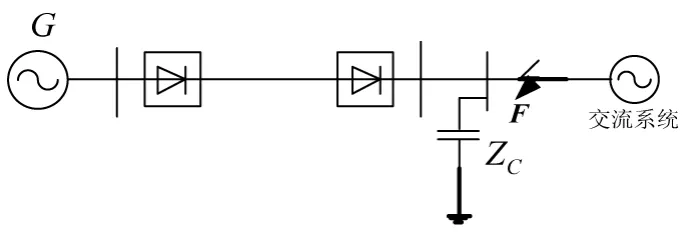
图4 HVDC仿真模型

由图1可以看出，UAB决定阀V1，V4的换相情况；UCA决定阀V5，V2的换相情况；UBC决定阀V3，V6的换相情况。通过仿真模型可以准确提取阀电流波形，通过阀电流波形可以准确定位每个阀的换相情况。

3.2 仿真结果

单就一次故障而言，故障时刻会影响到阀的换相情况。为了从整体上分析不同阀的换相失败情况，采取如下措施：故障以脉冲的形式在一个工频周期内施加在换流母线上10次，脉冲宽度为1/8个周波。每施加一次就仿真一次，以确定哪个阀发生了换相失败故障。然后从统计学的角度来分析每个阀的换相失败情况。

表3 A相接地故障换相失败概率统计

由表3可以得出如下结论：

1)A相接地故障时，阀V1，阀V4发生换相失败的概率最大；

2)过渡电阻较小时，由于其他阀的换流母线电压值比较低，因此也有可能发生换相失败故障；

3)随着过渡电阻的增大，阀V1，阀V4发生换相失败的概率降低；

4)当过渡电阻增大到一定值时，不再发生换相失败故障。

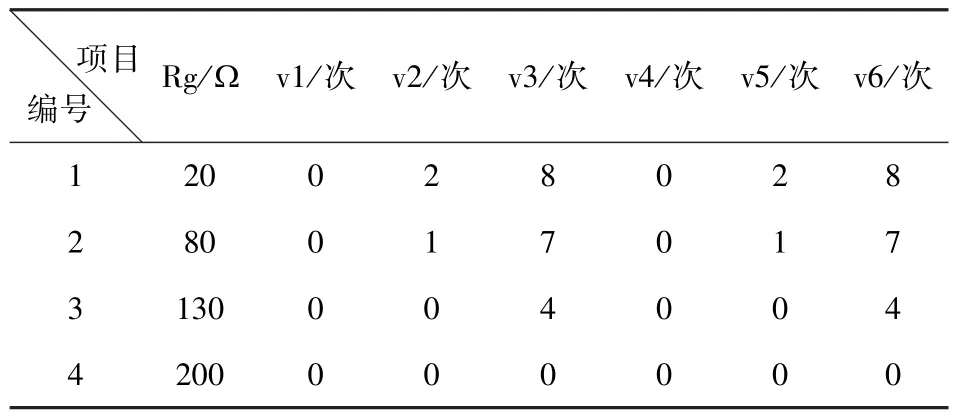
表4 BC两相接地故障换相失败概率统计

由表4可以得出以下结论：

3)同样的，当过渡电阻较大时，由于电压降非常有限，因此不再发生换相失败。

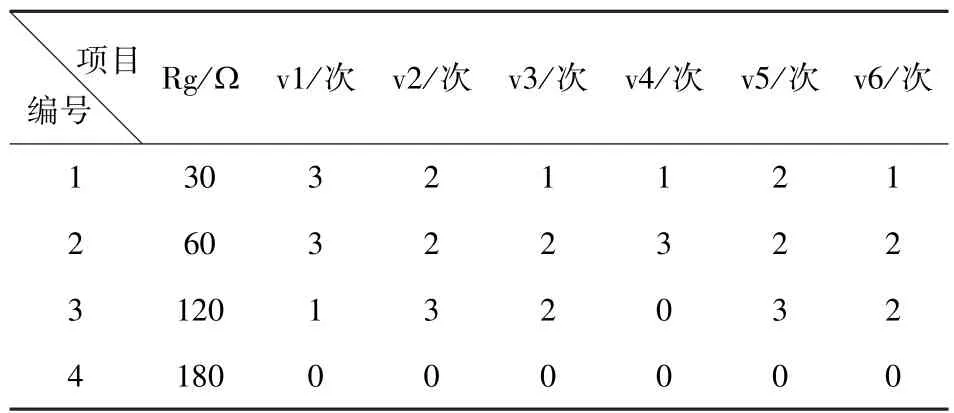
表5 三相接地故障换相失败概率统计

通过表5可以看出：

1)三相故障时每个阀都有发生换相失败的情况，不同的故障时间会引发不同阀发生换相失败故障；

2)同样的，当过渡电阻较大时，由于电压降非常有限，因此不再发生换相失败。

3.3 对换相失败的影响探讨

通过关断角的表达式可以看出，换相电压与过零点偏移是影响换相失败的两个重要因素。通过表1可得，CA线电压过零点虽然始终处于滞后状态，但由表3可以看出，阀V2在过渡电阻较小时也发生了换相失败故障；同时由表2可以得到，在BC接地故障下，由于CA线电压过零点始终处于超前状态，而且超前的角度很大，因此阀2与阀5可能会发生换相失败故障，但由表4可以看出，随着过渡电阻的增大，此时两个阀也不再发生换相失败故障；理论分析表明对称性故障时换相电压幅值下降，虽然线电压过零点始终滞后，但由表5可得换相电压幅值下降较大时仍然会引发换相失败故障。综合上面三种情况可以得出，换相电压幅值对换相失败的影响程度最大，过零点偏移仅仅是个辅助因素，并不是决定性因素。

4 结束语

1)交流系统故障容易引发换相失败。单相接地故障时，与故障相相连的阀发生换相失败的概率最大；两相接地短路时，由两故障相线电压决定换相的阀发生换相失败的概率最大；三相接地短路时，每个阀发生换相失败的概率是均等的。

2)由于过渡电阻的影响，换相电压与故障前电压的相位偏移关系可能会由超前变为滞后。

3)换相电压与线电压过零点偏移都会影响到阀的换相过程，但前者起主导作用。

[1] 浙江大学直流输电科研组.直流输电 [M].北京：电力工业出版社，1982：180-185.

[2] 余晓鹏，陆明，张振安，等.特高压直流对交流系统背景谐波的影响分析 [J].现代电力，2014，31(4)：39-43.

[3] 蔡恒，刘东兴，刘崇茹，等.特高压直流输电接入江西电网动态电压稳定分析 [J].现代电力，2011，28(6)：17 -22.

[4] 李新年，易俊，李柏青，等.直流输电系统换相失败仿真分析及运行情况统计 [J].电网技术，2012，36(6)：266-271.

[5] 王钢，李志铿，黄敏，等.HVDC输电系统换相失败的故障合闸角影响机理[J].电力系统自动化，2010，34(4)：49-54.

[6] 汪隆君，王钢，李海锋，等.交流系统故障诱发多直流馈入系统换相失败风险评估[J].电力系统自动化，2011，35(3)：9-14.

[7] 郝跃东，倪汝冰.HVDC换相失败影响因素分析 [J].高电压技术，2006，32(9)：38-41.

[8] 荆勇，欧开健，任震.交流单相故障对高压直流输电换相失败的影响[J].高电压技术，2004，30(3)：60-62.

[9] 邵震.高压直流系统换相失败对交流侧继电保护的影响[J].南方电网技术，2007，1(1)：72-80.

[10] 罗隆福，周金萍，李勇，等.HVDC换相失败典型暂态响应特性及其抑制措施 [J].电力自动化设备，2008，28 (4)：5-9.

Analysis on The Effects of AC Grounding Faults on HVDC Commutation Failure

YIN Guangli，LI Gan
(Changping State Grid of Beijing，Beijing 102200，China)

Detailed analysis of the relationship between commutation voltage reduction and line voltage zero-crossing point drift is given when various types of grounding faults occur in the AC system by using sequence components method.Thus systemic analysis about the impacts of grounding faults on commutation failure is presented.The results indicate that the influence on commutation process varies with fault types；the phase of commutation voltage may change from lead to lag compared to the voltage before faults as the transition resistance changes.The expression for extinction angle is modified correspondingly based on the theoretical analysis results.A simulation model based on CIGRE HVDC is built in PSCAD/EMTDC，verifying the correctness of the conclusion.Further discussion is presented about the effects of commutation voltage reduction and line voltage zero-crossing point phase shift on the commutation failure based on simulation results.

commutation failure；sequence components method；transition resistance；commutation voltage；phase-shift

TM74

B

1006-7345(2015)03-0029-06

2014-12-02

尹广利 (1978)，男，工程师，国网北京昌平供电公司，主要从事输电专业 (e-mail)yinguangli1978＠163.com。

李干 (1988)，男，助理工程师，国网北京昌平供电公司，主要从事输电运行管理等工作(e-mail)692076921＠qq.com。