三角环网输电线路故障测距范围延拓算法

纪思，李天权，杨桥伟，白冰，余多

(1.云南电网有限责任公司楚雄供电局，云南 楚雄 675000；2.昆明理工大学，昆明 650500)

三角环网输电线路故障测距范围延拓算法

纪思1，李天权1，杨桥伟1，白冰2，余多2

(1.云南电网有限责任公司楚雄供电局，云南 楚雄 675000；2.昆明理工大学，昆明 650500)

分析了三角环网输电线路故障后行波侧传播过程以及折反射规律。针对三角环网故障提出了一种故障测距范围的延拓方法。EMTDC/PSCAD仿真验证表明，所提出的三角环网故障测距延拓算法是可行的，故障定位结果准确可靠。

三角环网；故障测距；延拓

0 前言

输电线路距离长、跨度大，各种故障时有发生。快速、准确地确定线路故障位置，可有效保证电力系统运行的稳定运行。

作为故障测距的方法之一，行波法是利用故障行波在母线与故障点之间的传播时间来测定故障距离，其测距精度较高，适用范围较广。传统的行波测距方法仅能够对行波测距装置所监测的线路进行测距，而无法对未装设行波测距装置的线路进行故障测距。对由三个变电站之间输电线路组成的一个三角环网，若在每一个变电站内都装设行波测距装置对环网所有线路利用单端法或双端法进行故障定位，势必增加测距成本，而在仅装设两台行波测距装置的情况下，若其中一台装置未能及时启动或装置故障，则有一条线路将处于无行波测距装置监测的状态，因此，急需探索一种新的行波测距范围延拓方法，通过一台行波测距装置实现对整个三角环网的准确测距。

本文利用三角环网的故障行波传播特性，提出了一种三角环网故障测距延拓算法。理论仿真以及采用实际电网高速记录的电磁暂态数据所进行的分析表明，此方法对于非测距装置监测线路的故障定位具有准确的测距效果。

1 三角环网线路故障行波特性

1.1 故障初始行波

当前的行波测距装置普遍是基于故障线路上观测到的故障行波来进行分析，进而实现故障定位。输电线路故障后，初始行波会发生折反射，当行波浪涌到达输电线路两端时会发生反射与折射，到达故障点时也会发生反射与折射。下面具体说明环网故障情况下的几种突出的行波传输路径。如图1所示的M、N、P组成的传输网络，当MN之间的F点发生故障后，故障行波将会沿线路传播并发生折反射：

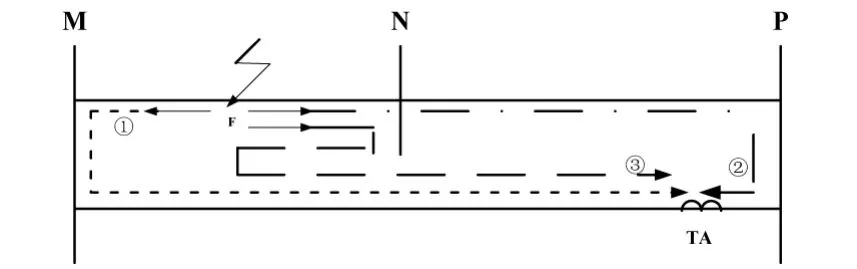
图1 行波传播路径图

1)为故障初始行波经母线M反射后传播到的量测端的初始行波；

2)为故障行波经N母线投射到健全线路NP后并经P母线反射的相邻母线反射波；

3)为故障行波经N母线反射又经故障点F反射的故障点反射波。

对于输电线路行波故障测距，各行波分量的极性关系非常重要。有效地辨识测量母线处暂态初始行波、故障点反射波、对端母线反射波以及相邻母线反射波间的极性关系，可以更为准确地实现故障测距。

根据文献 [1]将母线分为三类：第一类，母线上接有三回及以上进出线同时接有变压器；第二类，母线上接有两回进出线同时接有变压器；第三类，母线上只接有故障线路而无其它出线。

根据文献 [2]定义的输电线路折反射系数，分析行波传播规律可知：各行波分量间的极性关系由各折反射系数决定：当母线M、N均为第一类母线时，必有βm、βn小于零；当母线M、N为第二类母线时，由于变压器及母线部分电容的影响，初始反射系数为-1；当母线M、N为第三类母线时βf也小于零且与过渡电阻的大小无关，即故障点反射波分量与初始行波极性相同，而对端母线反射波与初始行波极性相反。这个结论对于暂态电压及电流行波均成立[3]。

对于如图2所示的ABC三个变电站组成的三角形环网，当输电线路AB在F点发生故障后，对于健全线路AC，除存在初始正向行波经B、C两站两级透射后到达观测点A外，还存在着初始故障行波沿故障线经A站透射至健全线AC并在其末端反射回观测点A的行波[4]，故障初始行波在三角形环网中的传播路径如图2所示。

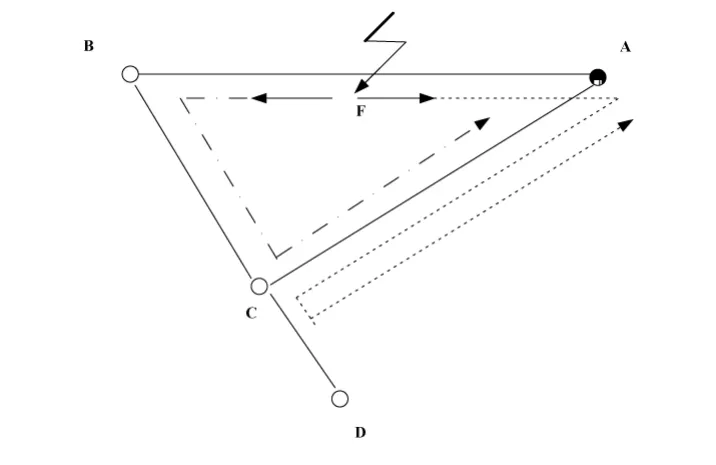
图2 故障初始行波在三角环网中的传播

设故障点F距量测端A的长度为x，βA为观测点A处的反射系数；αA为观测点A处的折射系数；βC为C处的反射系数；ZC为C处的等效波阻抗；uf、Rf分别为故障点处的附加电源和电阻，则根据初始故障行波传至观测点的路径长度关系可得：当故障点距离A端的距离满足：

等价于健全线路AC与故障线路AB的故障行波波头到达观测点A的时间差满足：

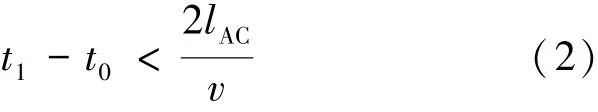
时，健全线路末端反射波晚于健全线路故障行波到达观测点，不会对测距结果造成影响。推导得到健全线末端反射波表达式可以写为：

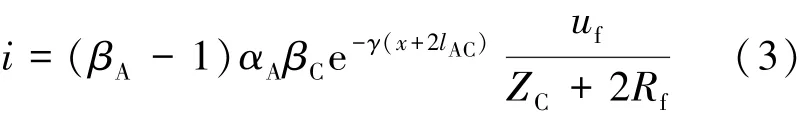
如果C站除与A、B两站的连接以外还有D站的出线，则A站的健全线还可以观测到来自CD末端的反射波，即：

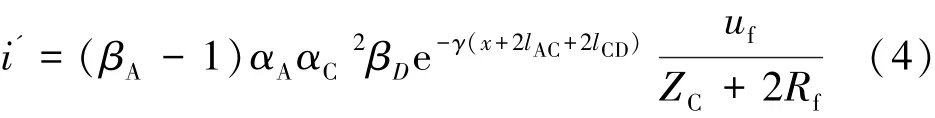
来自CD末端的反射波i'的极性与D站的母线出线数相关，同时由于经过C站的两次透射和D站的一次反射，行波会发生衰减，进而幅值有所降低，但是不会影响测距波头辨识。

1.2 测距模量计算

线路三相之间存在电磁耦合，直接利用相量行波进行故障分析比较困难，所以可利用相模变换，将三相线路的行波分解为三个独立的模分量。模分量可分为两类，一类是通过大地传播的行波，称为零模分量；另一类是不通过大地传播的行波，称为线模分量。输电线路发生非对称接地故障后，线模行波和零模行波会分别沿线模传播通道和零模传播通道在线路上传播。除故障点外，输电线路都能够解耦，线模行波和零模行波之间不会发生交叉透射，行波会在线路末端和故障点之间来回折反射；在故障点处，由线路末端反射到达故障点的行波会在故障点发生交叉透射。线模行波在线模通道传播的过程中，10 kHz以上频率成分的波速几乎相等，相对于传播了相同距离的零模行波，波形的衰减和畸变较小，透射进入零模通道的线模行波幅值、斜率较大，将污染零模通道的零模行波。

凯伦贝尔变换、克拉克变换、Wedpohl变换[5]是目前电力系统中普遍使用的变换，它们在时域问题的分析中被广泛应用。在继电保护中广泛应用的相模矩阵在时域下计算得到模量均不能实现单一模量反映所有故障类型[6]，而必须与双模量相配合，从而大大增加了实际工程计算量。

宋国兵等学者总结各类相模变换的特点和不足，提出了一种新的相模变换矩阵，这种新的相模变换矩阵中单一模量即可以反映所有故障类型。针对均匀换位线路构造出的相模变换矩阵[7]，其原始矩阵为：

对原始矩阵进行施密特单位正交化得到：

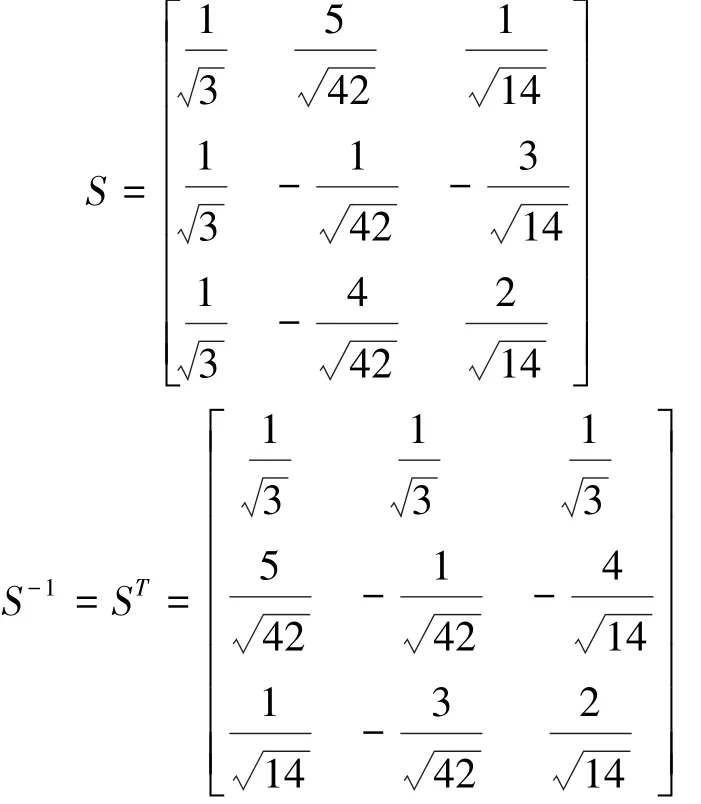
这种新的模变换矩阵得到的模量值在所有故障类型下均为非0值，即1模值或2模值均能单一模量反映所有故障类型。本文将利用这种新的相模变换矩阵对均匀换位输电线路进行解耦[5]，在EMTDC/PSCAD中按如图3所示的方法提取行波线模分量。类似的，还可以实现行波零模分量的提取。

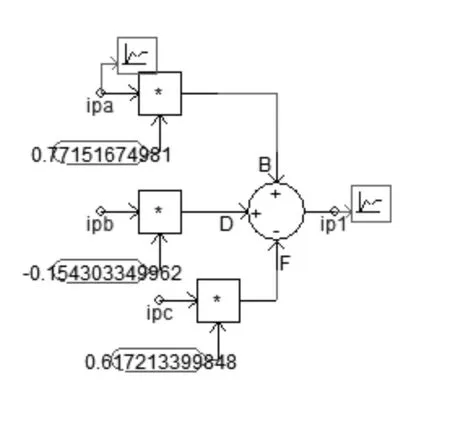
图3 行波线模分量提取

1.3 行波波速的选取

行波法故障定位按照测距原理可以分为单端测距和双端测距[8-9]，波速是影响行波测距的主要因素，高压输电线路的架空线结构和大地的电阻率决定了波速的大小[10]，土壤电阻率受气候的影响比较明显，线路的分布电感因不同的地区和线路结构而异，分布电容与分布电感的变化会影响行波线模分量与零模分量的传播速度。此外，线路参数还与频率相关，正序电阻由于导线的集肤效应而随频率上升，正序电感基本不随频率而变化，零序电阻随频率上升的现象除了与集肤效应有关外，还与大地的电阻有一定关系，零序电感则由于地中电流穿透深度的变化而随频率下降；因此零序参数的变化更为剧烈，零模分量传播速度的变化范围也更大[10]。目前，波速的选取方式有两种，即：经验法和利用线路参数计算行波波速。

1.3.1 经验法

由于波速是一个不确定的量，工程中一般根据不同的输电线路电压等级选择一个接近光速的值来近似表示波速，波速取值为 0.936c(110 kV)[11]到0.987c(500 kV)[10]不等，即是所谓的经验波速。

1.3.2 用线路参数计算行波波速

工程实际中，输电线路的每个杆塔的型号、导线和地线型号、分裂导线数等都是已知的[12]，则该线路的结构参数即是确定的。可以由该输电线路所用主要杆塔型号和结构参数利用Matlab仿真求出该线路各模量的速度。

线模波速可由线路参数近似计算得到，线模分量的波速在不考虑频率的影响时比较稳定；然而，零模分量则随频率的变化存在着较严重的衰减，导致行波衰耗大且波速不稳定，对定位精度影响也较大[13]。若将输电线路近似为无损线路，且不考虑参数的频率相关性时，线路的线模分量与零模分量的行波速度计算公式可表示为

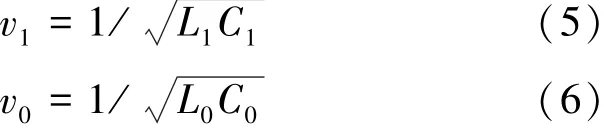
式 (5)和 (6)中，L1、C1、L0、C0分别为单位长度线路的正序电感、正序电容、零序电感、零序电容。

本文中在PSCAD仿真模型中对三角环网故障测距延拓方法进行验证，因此将波速取为经验波速v=2.98×108m/s。

2 三角环网输电线路故障测距

对于三角环网输电线路，若仅在M端母线处安装行波测距装置，则三角环网输电线路故障后的初始行波的折反射过程如图3所示，当行波浪涌到达输电线路两端时会发生反射与折射，到达故障点时也会发生反射和折射，通过母线折反射后的故障行波分别先后到达量测端M。

图4中：M、N、P为三角环网输电线路的三端母线，F为故障点，l1为MN段线路全长，l2为NP段线路全长，l3为MP段线路全长，故障初始行波到达母线N端并经母线N透射到健全线路l1后，量测端TA1获得的故障波头时间为t1；故障初始行波到达母线P端并经母线P透射到健全线路l3后再经母线M端透射到健全线路l1时，量测端TA1获得的故障波头时间记为t2。

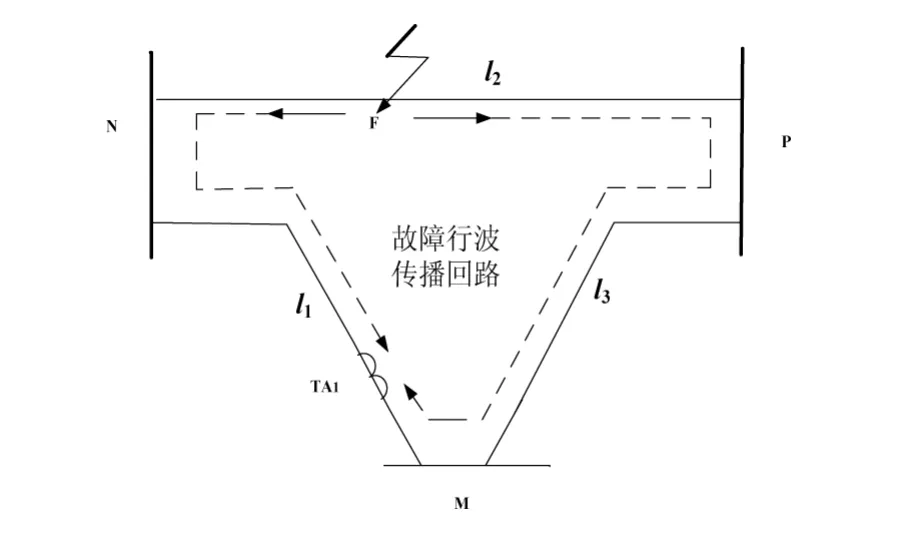
图4 三角环网故障行波传播路径图

根据两次故障首波头的时间t1，t2，求取首波头的时间差为Δt=t1-t2；按照公式x=(v·Δt -l1+l2+l3) /2进行故障位置的计算。其中，l1，l2，l3分别为组成三角环网的三条线路，故障线路为l3；x为故障点距离母线N的距离；v为波速。

3 故障仿真分析验证

3.1 仿真模型

如图5所示的三角环网输电线路，下面对仿真模型参数进行说明：三端发电机总容量100 MVA，线电压为525 kV，频率为50 Hz；变压器为Dyn型接线，变比为525/230 kV；各条线路长度分别为：l1=150 km，l2=100 km，l3=90 km；线路采用频变模型；母线处的杂散电容均取为C =0.1 μF。

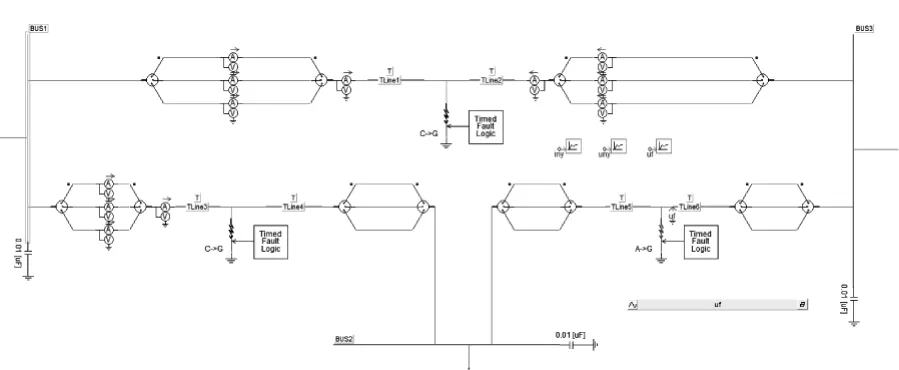
图5 三角环网仿真模型图

3.2 故障仿真

1)线路l2距离母线N端40 km处发生A相接地故障，故障初始角为90°，过渡电阻为10 Ω，采样率为1 MHz。仿真得到的故障电流行波如图6所示。

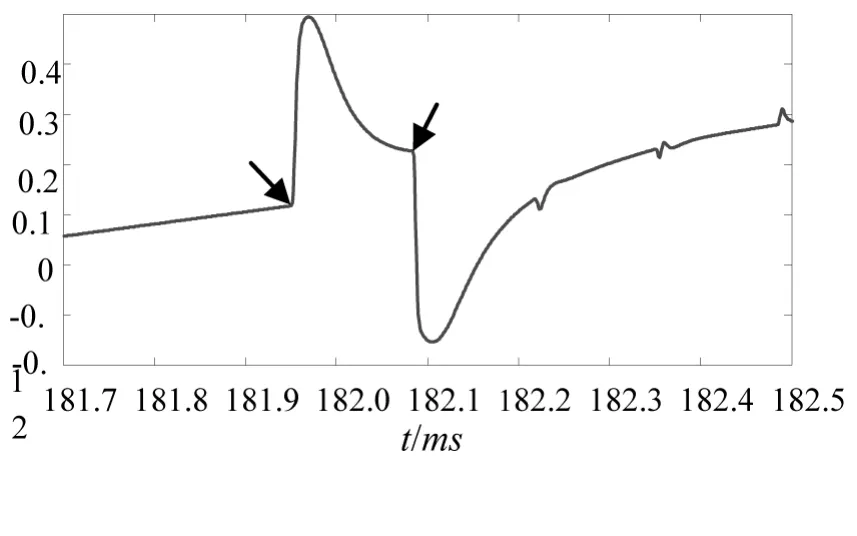
图6 距N端40 km处故障时电流行波波形图

根据图6所示的电流行波图找出两次故障首波头对应的时间t1=0.182 081 s，t2=0.181 949 s；求得首波头时间差Δt=t1-t2=0.000 132 s，v取为经验波速，大小为2.98×108m/s；利用公式计算故障距离即：x= (v·Δt-l1+l2+l3)/2= 39.668 km。由此可见，实际误差x0=40-39.668 =0.312 km＜500 m，与实际线路长路相比具有比较好的测距精度。

2)线路l2距离母线N端55 km处发生A相接地故障，故障初始角为60°，过渡电阻为10 Ω，采样率为1 MHz。

图7 距N端55 km处故障时电流行波波形图

根据图7所示的电流行波图找出两次故障首波头对应的时间t1=0.161 009 s，t2=0.160 770s；求故障首波头时间差Δt=t1-t2=0.000 239 s，v取为经验波速，大小为2.98×108m/s；利用公式计算故障距离x=(v·Δt-l1+l2+l3)/2=55.611 km。由此可见，实际误差x0=55-55.611=0.661 km，与实际线路长路相比具有比较好的测距精度。

本文做了大量仿真实验以验证所提测距方法的准确性，分别列出了A相接地故障、不同过渡电阻情况下的部分仿真测距结果及其误差。应用本文所提方法对架空线的故障定位误差跟故障距离相比均在允许范围之内，双端测距的一般误差。此方法消除了双端[14-16]测距两端时间的同步误差，其原理简单，且不受故障瞬时性、故障过渡电阻变化等因素的影响，测距结果准确可靠，是三角环网故障测距的一种范围延拓方法。应用此方法可以精确定位线路故障点，对于线路故障修复和维护线路安全运行具有十分重要意义。

4 结束语

1)行波波头突变大小与其经过的阻抗不连续点次数及阻抗不连续点性质有直接关系。

2)在某一变电站内安装行波测距装置，当环网中未被行波测距装置监测的输电线路发生故障后，故障初始行波到达故障线路两端变电站，并经母线透射到环网中的健全线路上，通过行波测距装置采集两条健全线路量测端的电流行波并记录故障初始行波到达量测端的时间，然后求其时间差，最后利用三角环网各线路长度以及经验波速进行故障定位。

3)利用EMTDC/PSCAD进行大量仿真表明，本文所提出的三角环网故障测距延拓算法是可行的，故障定位结果准确可靠。

[1] 董新洲.小波理论应用于输电线路故障测距研究 [D].西安：西安交通大学，1996.

[2] 吴维韩，张芳榴，等.电力系统过电压数值计算 [M].北京：科学出版社，1989.

[3] 束洪春，李义，宣映霞，等.对不受波速影响的输电线路单端行波法故障测距的探讨 [J].继电器，2006，36 (8)：1-6.

[4] 张广斌.实测数据环境下的输电线路行波故障测距关键技术研究 [D].哈尔滨工业大学，2014.

[5] 王安定，葛耀中.模量变换技术在反应故障分量的微机保护中的应用研究 [J].电力系统自动化，1988，12(3)：17-27.

[6] 敬涵，张飚，范瑜，等.解耦变换在电力系统暂态保护中的应用研究 [J].北京交通大学学报，2006，300(5)：101-104.

[7] 宋国兵，李森，康小宁，等.一种新相模变换矩阵 [J].电力系统自动化，2007，31(14)：57-60.

[8] 尹晓光，宋琳琳，尤志，等.与波速无关的输电线路双端行波故障测距研究 [J].电力系统保护与控制，2011，39 (1)：35-39.

[9] 郑秀玉，丁坚勇，黄娜.输电线路单端故障定位的阻抗行波组合算法 [J].电力系统保护与控制，2010，38(6)：18-21.

[10] 邓军波，施围.输电线路接地故障行波测距新方法 [J] .继电器，2000，28(8)：16-18.

[11] GALE P F，TALOR PV，HITCHIN C.Traveling wave fault locator experience on Eskom’S transmission network[C]. //Seventh International Conference on Developments in Power System Amsterdam(Netherlands)：2001：327-330.

[12] 覃剑，陈祥训，郑健超，等.利用小波变换的双端行波测距新方法 [J].中国电机工程学报，2000，20(8)：6 -10.

[13] 黄雄，王志华，尹项根，等.高压输电线路行波测距的行波波速确定方法 [J].电网技术，2004，28(19)：34 -37.

[14] 葛耀中.新型继电保护和故障测距的原理与技术 (2版) [M].西安：西安交通大学出版社，2007.

[15] 徐丙垠，李京，陈平，等.现代行波测距技术及其应用[J].电力系统自动化，2001，25(23)：62-65.

[16] 陈平，徐丙垠，李京，等.现代行波故障测距装置及其运行经验 [J].电力系统自动化，2003，27(6)：66-69.

李天权，男，工程师，云南电网有限责任公司楚雄供电局，从事调度运行方面研究工作。

杨桥伟，男，工程师，云南电网有限责任公司楚雄供电局，从事调度运行方面研究工作。

Research on Triangle Ring Transmission Line Fault Range Extension Algorithm

JI Si1，LI Tianquan1，YANG Qiaowei1，BAI Bing2，YU Duo2
(1.Chuxiong Power Supply Bureau，Yunnan Power Grid Co.，Chuxiong，Yunnan 675000，China；2.Kunming University of Science and Technology，Kunming 650500，China)

Analysis the fault traveling wave propagation and reflection rule about the triangular ring network transmission line.To propose a fault location method for the triangular ring network.EMTDC/PSCAD simulation results show that，the extension algorithm for triangular ring network fault location is feasible，the results of fault location is accurate and reliable.

triangular ring network；fault location；extension

TM73

B

1006-7345(2015)03-0004-05

2014-12-22

纪思 (1985)，男，硕士，工程师，云南电网有限责任公司楚雄供电局，从事调度运行方面研究工作，(e-mail)282685687＠qq.com。