旋转体零件中心偏置时测点坐标值的求解方法

刘兴富

(广州威而信精密仪器有限公司，陕西西安 710075)

旋转体零件中心偏置时测点坐标值的求解方法

刘兴富

(广州威而信精密仪器有限公司，陕西西安 710075)

针对传统的测量旋转体零件参数时需要将被测零件基准孔(轴)圆心与分度台旋转中心调整重合的问题，受坐标系平移方法的启迪，提出在分度台上任意放置被测零件时测点坐标值的求解方法，这种方法省时、省力，效率高，且可达到精密测量的要求。

分度台；偏置测件；求解方法

0 概述

按极坐标系统进行旋转体零件参数测量时，传统测量程序(步骤)是：

(1)确定分度台旋转中心的坐标值；

(2)调整被测零件基准孔(轴)圆心与分度台旋转中心相重合；

(3)进行零件的参数测量。

调整被测零件基准孔(轴)圆心与分度台旋转中心相重合，传统的方法是要调整被测零件的旋转中心严格与分度台的旋转中心重合，以达到零件参数精密测量所要求的准确度，被测件位置调整困难，取得正确位置费时、费力，效率低。

针对传统方法的缺点，提出一种偏置被测件的方法。

1 安装调整方法的比较

如图1所示，被测零件基准孔(轴)圆心与分度台旋转中心相重合。当分度台旋转时，被测零件上的每个质点都围绕分度台旋转中心作圆周运动，零件上各被测孔(轴)的圆心也可看成是一个质点。

传统方法的优点是：测量者易于理解，测量基准完全与设计基准重合；缺点是：需要将被测零件基准孔(轴)圆心与分度台旋转中心调整为相重合，被测件在调整位置时移动困难，取得正确位置费时、费力，效率低。

偏置被测件的方法，只需要将被测零件随意地放置在分度台上，省时、省力，效率高。

2 虚拟坐标设定和计算方法

(1)调整步骤和数据提取

①首先确定零件旋转中心零点(X1,Y1)坐标；

②确定零件中心(X1,Y1)到分度台旋转中心(X0,Y0)的距离为L、H(注意：由于零件位置放置不一样，L、H可能是负数或正数)。

(2)测量原理与公式推导

根据图2得到图3几何示意图，并推导出相关参数的计算公式。

应先指出：分度台逆转时针旋转时转角正,顺时针旋转时转角为负。

如图3所示，设O为分度台旋转中心，O1为零件旋转前的旋转中心，Oi为零件旋转后的旋转中心。

当在O1位置测量完B轴的孔1后，将分度台旋转φi角，测量孔i，得到坐标Oi；这时只需计算出O1到Oi的X向和Y向的移动量，即M和N。具体计算公式推导过程如下：

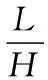
OC=Rcosθ=Rcos(φi-α)=R(cosαcosφi+sinαsinφi)

OiC=Rsinθ=Rsin(φi-α)=R(sinφicosα-cosφisinα)

O1E=O1D+DE(OiC)=L+R(cosαcosφi+sinαsinφi)

所以可得：

式中:M和N分别为零件坐标系从O1旋转到Oi的X向和Y向的移动距离；α为工作台旋转中心和零件中心连线与纵轴间的夹角；L和H为零件中心O1的坐标值；R为零件中心旋转轨迹圆半径；φi=0(0°)～5(300°)为工作台-零件的旋转角度。

3 程序的编制

(1)程序设置。在程序中首先将零件中心坐标系O1设定到测量坐标系O中，并输入以下参数值：零件中心(X1，Y1)到分度台旋转中心(X0，Y0)的距离为L、H；φ0(工件所要旋转的起始角度，如图2中第1孔的角度，即B轴为0°)；φi(工件所要测量每次旋转的角度，见图2)；φ5(工件所要转到的最终角度，如图2中的φ5为最终角度，φ5=300°或者φ5=-60°)。

(2)程序编制(略)。

4 结束语

传统方法必须把零件基准孔(轴)中心调整为和分度台旋转中心重合，才能对零件参数进行测量，调整困难，费时、费力，效率低。而偏置被测件的新方法，只需将被测零件随意地放置在分度台上，不必对零件的位置进行任何调整，省时、省力，效率高。

综上所述，在测量旋转体零件参数时，零件偏置新方法(坐标系平移方法)具有非常大的优势，特别是测量大型旋转体零件时，更具有良好的效果。

最后应指出的是，为简化计算，偏置时旋转体零件中心应尽量靠近分度台的旋转中心。

【1】刘兴富.分度台旋转中心坐标快速确定[J].机械工人:冷加工，2004(1):57.

【2】刘兴富.坐标变换在精密测量中的应用[J].计量技术，2011(6):38-41.

【3】李慎安.测量误差及数据处理技术规范解说[M].北京:中国计量出版社，1993.

SolvingMethodofMeasuredPointsCoordinateofRotatingBodyPartswithCenterBias

LIU Xingfu

(Guangzhou Wilson Precision Instruments Co.,Ltd.,Xi’an Shaanxi 710075，China)

In traditional measuring to parts with rotating body, the center of benchmark holes (axis) of measured parts is need to be adjusted in superposition with the rotation center of indexing table. To overcome the problem, enlightened by translating coordinate method, the solving method of coordinate was put forward in which the measured parts was put on the indexing table randomly. This method can save time and labor, has high efficiency, and can reach the requirements of precision measurement.

Indexing table; Bias measured parts; Solving method

2014-10-21

刘兴富(1935—)，男，高级工程师，研究领域是几何量精密测试。E-mail：xall029@163.com。