箱涵结构不同计算模型的精度分析

蒲德龙　李立坤

(1.贵州省交通规划勘察设计研究院股份有限公司　贵阳　550081；　2.中交二公局第一工程有限公司　武汉　430014)

箱涵结构不同计算模型的精度分析

蒲德龙1李立坤2

(1.贵州省交通规划勘察设计研究院股份有限公司贵阳550081；2.中交二公局第一工程有限公司武汉430014)

摘要运用结构力学简化计算及Midas有限元通用软件，对公路工程中某一常用的通用箱涵结构进行了空间结构受力分析。结果表明，结构力学简化计算的结果与有限元的计算结果有一定的差距，有限元模型中，用不同单元类型模拟箱涵结构，也存在较大的差别，其中梁单元与板单元的计算结果基本一致，但实体单元的计算结果比其他方法计算的均要小很多；此外，箱涵结构地基支撑刚度也会影响结构的受力；小构件的箱涵结构，结构受力并不是简单的梁、板单元受力特性，而是一个复杂的空间受力状况。

关键词公路工程通用箱涵Midas FEA地基刚度

对于公路工程中通用箱涵的受力分析，现行的计算理论主要把空间问题转化为平面问题，结合结构力学和箱涵计算软件，对箱涵进行配筋计算和结构验算。然而，大部分的实际箱涵结构，都是与路线走向有一定的角度，有研究表明[1-2]，当斜交角度小于某一个值时，可以不考虑斜交的影响。近些年各大设计院普遍采用斜交转正交来计算箱涵。当然，对于斜交角度过大的的箱涵，也有其相应的计算理论，那就是通过空间计算结构的弯矩和扭矩，再以主方向上的弯矩和扭矩进行设计配筋。对于这种斜交计算理论，海潮等[3]对其做了研究，王丽等[4]对斜交地道桥的力学特性做了研究，其研究的主要内容是结构的弯矩随斜交角度的变换情况，对于结构边界条件支撑刚度的影响等问题并没有涉猎。目前为止，无论是斜交箱涵还是正交箱涵，做的研究工作，都是在一种计算模式下进行的，并未考虑计算模型的精度，同时，边界条件均是假定在一个半无限大的弹性体上[5-6]，在支撑刚度处理上，支撑刚度对结构受力的影响并没有做深入的分析。本文对一通用标准箱涵进行多种计算模型下的结构受力分析，得出相关结论，供箱涵结构工程人员参考。

1　工程概况

本合同段为牙同高速公路D标段，项目起点位于青海省海东地区化隆县哇加滩附近，设计起点桩号为K32+000，路线向南先后跨越S203省道和黄河，再由隆务峡1号长隧道穿越山体，出隧道后，路线终于青海省黄南州尖扎县当顺乡隆务峡口林业资源管理站附近，终点桩号为K37+000，路线全长5.012km。其中共有13处钢筋盖板涵和通道。

选取其中一座箱涵进行结构受力分析，结构尺寸及受力情况见图1、图2，设计参数及荷载参数见表1和表2。

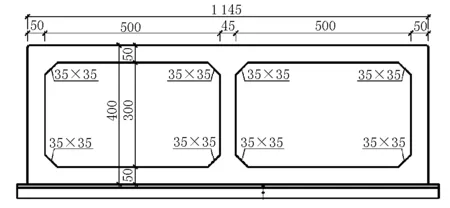
图1　结构尺寸图(单位：cm)

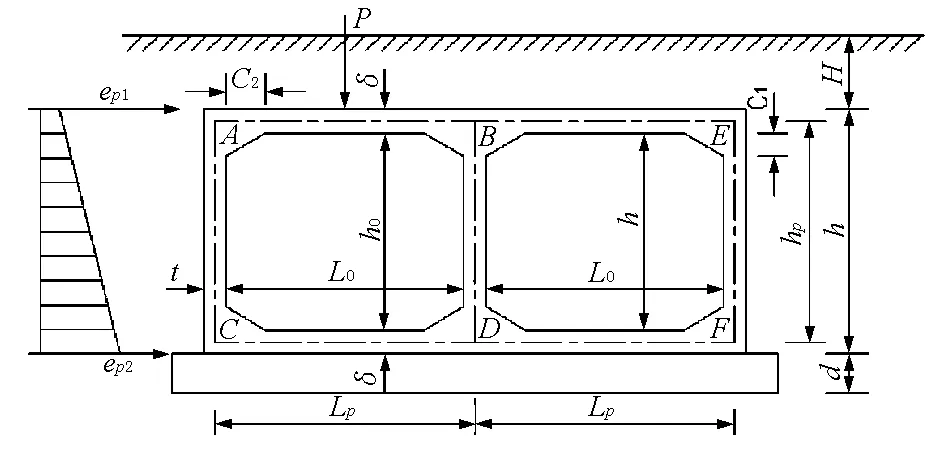
图2　结构受力简图

表2　荷载参数　kPa

2　模型建立及基本假定

本箱涵结构的有限元模型分为平面杆系模型，空间板单元模型以及空间实体单元模型；杆系模型和板单元模型均考虑单元外偏心、无偏心、内偏心3种情况，此外，由于箱涵看作为支撑在半无限体上的空间结构，在荷载或其他作用下，结构是与地基一起发生变形的，故而，本模型考虑了地基支撑刚度对结构受力的影响。

有限元模型基本假定：①箱涵结构底面各点的支撑刚度一致；②不考虑箱涵结构与地基的摩擦作用。实体模型离散图见图3。

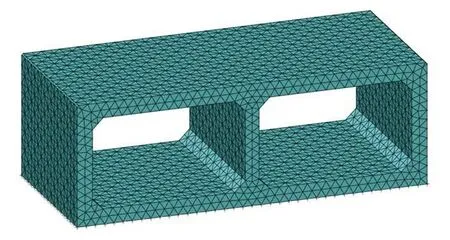
图3　空间实体模型单元离散图

3　内力计算及分析

对箱涵中的钢筋和混凝土进行受力分析，在最不利荷载作用(1.2恒载+1.4活载)下，与结构力学简化计算所得的内力进行对比，表3～表5为几种计算方法所得的弯矩内力和应力值。

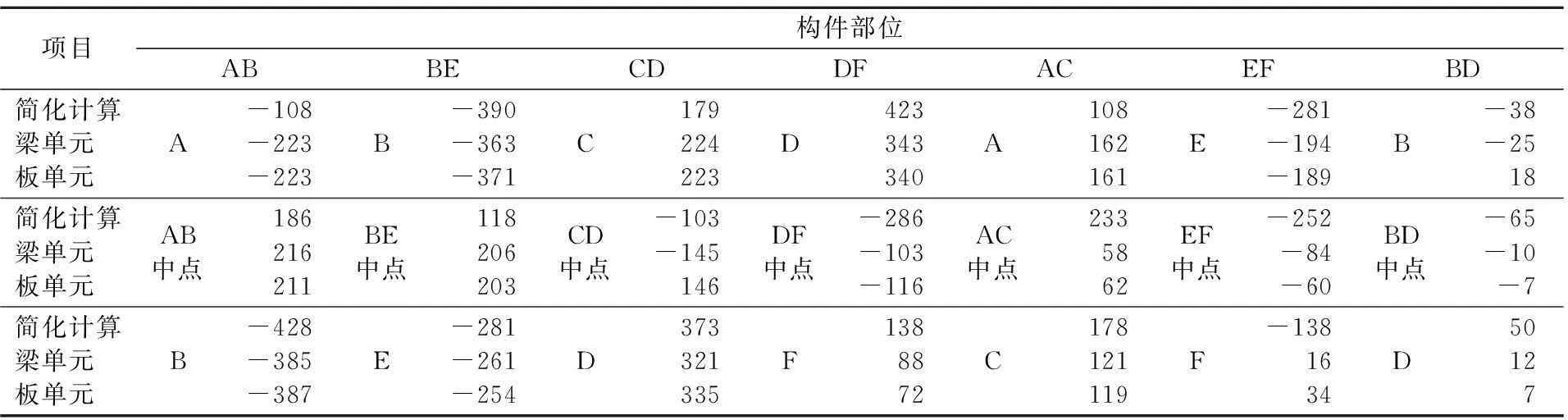
表3　箱涵弯矩内力值比较表　kN·m

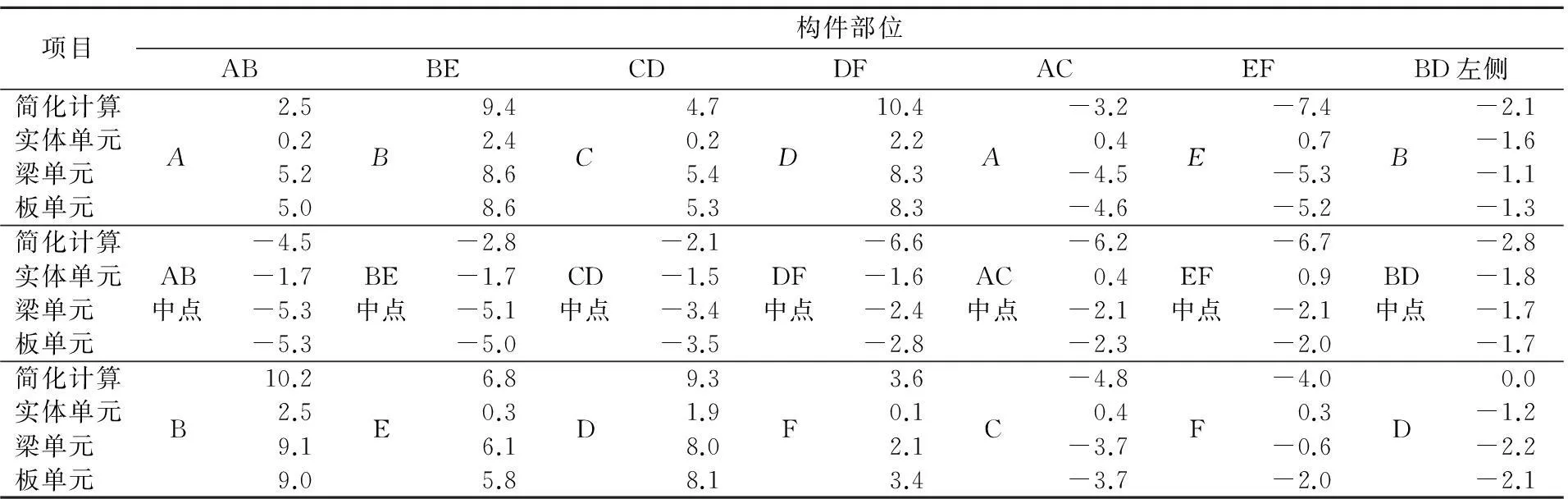
注：构建受压为正。

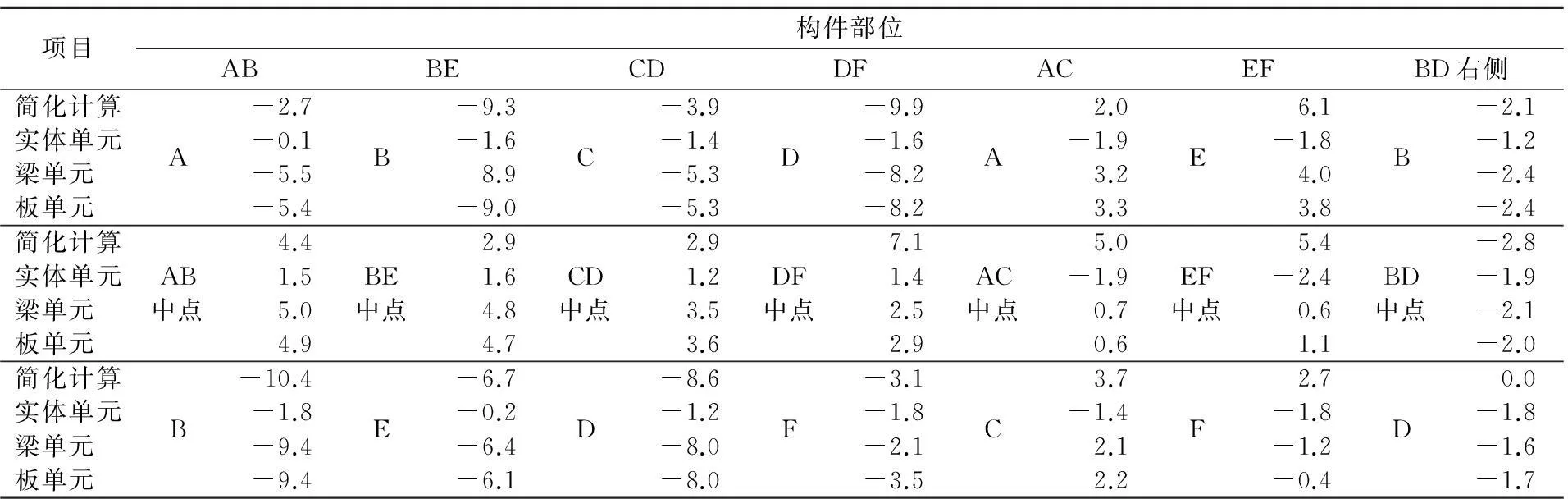
表5　箱涵构件内侧应力比较表　MPa

由表3可见，箱涵构件各部分在最不利荷载组合下，简化计算结果与有限元程序算的结果有一定的差距，箱涵顶板的误差最大为52%，最小5%；箱涵底板误差最大为178%，最小11%；箱涵腹板误差最大为963%，最小33%。而有限元的计算结果，3种方法之间的误差却很小，箱涵底板的误差最大为3%，最小0%；箱涵底板误差最大为18%，最小0%；箱涵腹板误差最大为113%，最小0%。从数据变化情况来看，除个别点外，梁、板单元有限元的计算结果，能很好地吻合，而简化计算与有限元计算之间有很大的差距，特别是腹板的计算；误差大的原因是除了是由于数据量太小，导致误差的百分率很大外，另外箱涵简化计算边界条件的部分假定，对腹板和底板的受力有很大影响。

图4　空间实体单元应力图

从表4、表5，以及图4的箱涵构件应力计算结果来看，梁、板单元模型的应力值，除腹板和底板的个别点外，大部分关键位置的应力值很接近，比如顶板位置以及底板位置都能吻合得好。但实体单元的应力计算结果要远小于简化计算和梁、板单元模型的计算结果，部分位置的应力计算结果，简化计算与梁、板单元模型计算结果能很好地吻合，而与实体单元模型的计算结果有很大的差距，比如BE构件的B位置内侧，实体单元模型的应力只有1.6MPa，而其他3种计算方法都在9MPa左右，并且大部分构件的应力值要远小于简化计算和梁、板单元模型的计算。

分析原因，对于小构件的箱涵结构，结构受力并不是简单的梁、板单元受力特性，而是一个复杂的空间受力。对于弯曲平面尺寸大于1/10的构件，截面变形不满足平截面假定，而梁、板模型均是基于变形协调的平截面假定基础上进行，使得梁、板模型的计算结果偏大，模拟失真。此外，实体单元底板为一个面的边界条件，而简化计算和梁、板单元模型底板的约束情况集中到底板节点上，与实际的受力状况有一定偏差，对于结构受力不是简单梁、板单元受力特性的小构件的箱涵来说，这种边界条件偏差的影响会更大。

4　结论

(1) 构件内力方面，现行的简化计算结果与有限元的计算结果有一定的差距，并且还与箱涵构件位置有关。

(2) 箱涵边界条件的假定，对腹板和底板的受力影响要大于顶板，并且把底板的约束情况集中到底板节点上，与实际的受力状况会有一定偏差。

(3) 箱涵实体空间模型与简化计算、梁、板单元的平面模型，计算结果有很大的差距，空间实体模型应力值要远小于平面模型的应力值，说明小构件的箱涵结构，结构受力是一个复杂的空间受力状况，杆系模型模拟会失真，实体模型模拟相对要可靠。

(4) 按平面杆系计算结果来对箱涵结构进行配筋，箱涵结构的安全系数会很大。

参考文献

[1]范立础.桥梁工程[M].北京:人民交通出版社,2001.

[2]林文泉,朱尔玉,田杰.框架式地道桥考虑纠偏内力影响的结构优化设计[J].路基工程,2005(5):4-7.

[3]禹国辉,朱尔玉,李学民.斜交框架箱涵结构在钝角处的受力和配筋特点[J].北京交通大学学报,37(1):125-127.

[4]王丽,季日臣,伊新芳,等.斜交框架地道桥的力学特性[J].甘肃科学学报,2009,21(1):132-134.

[5]金理平,金明亮.地道桥的有限元法结构分析[J].甘肃科技纵横,2009,38(1)：158-158.

[6]潘文怡.斜交框架地道桥的设计探讨[J].铁道标准设计,2009(6):79-81.

收稿日期：2015-04-11

DOI10.3963/j.issn.1671-7570.2015.04.026