预应力混凝土T梁非线性分析

王国强　张红宇　吴文清

(1.江西省交通工程集团公司　南昌　330008；　2.南昌市公路勘察设计院　南昌　330006；

3.江西省高速集团宜春管理中心　宜春　336000)

预应力混凝土T梁非线性分析

王国强1张红宇2吴文清3

(1.江西省交通工程集团公司南昌330008；2.南昌市公路勘察设计院南昌330006；

3.江西省高速集团宜春管理中心宜春336000)

摘要为了研究预应力混凝凝土T梁开裂后的力学性能，选取30 m预应力混凝土T形梁为原型，以有限元理论为基础，采用三维弹塑性实体空间有限元法对实桥三分点加载全过程进行非线性静力仿真分析，获取了桥梁加载全过程的变形、裂缝等结构响应发展规律，研究了桥梁的受力特性、破坏机理，计算结果表明：运用ANSYS模拟得到结论和试验结果符合较好。

关键词预应力混凝土梁非线性受力特性

随着日益增多的交通量，以及超载和养护缺位等多种因素的影响，在役预应力混凝土T梁桥普遍存在裂缝、过度下挠等病害，使得在役桥梁的承载能力受到一定程度的威胁[1-2]。然而，现在对其开裂后的力学性能的研究尚且不够，特别是极限状态下的力学性能缺乏全面了解。目前，随着更为精确的弹塑性分析理论被建立起来，并被运用于预应力混凝土桥梁结构非线性分析，由于该理论综合考虑了结构几何、材料非线性的影响，故采用该理论计算出的临界荷载能较真实地反映结构的承载能力[3-4]。本文正是在此基础之上，采用大型通用有限元软件ANSYS对我国桥梁建设中常用30 m T梁进行非线性有限元仿真，采用预应力混凝土结构常用有限元模型、整体式模型和分离式模型相结合的方法，进行非线性受力状态的模拟和破坏机理的研究。

1　数值模拟

1.1基本假定

为了建立预应力混凝土T梁的有限元计算模型，在对预应力混凝土T梁进行截面分析时，由于其长度远大于截面尺寸，采用如下基本假设。

(1) 假定钢筋与混凝土接触面位移协调，不考虑两者之间的粘结滑移。

(2) 不考虑时间(龄期)和环境温、湿度等的作用。

(3) 忽略了加载前的预应力损失。

1.2有限元单元选择和特性

根据预应力混凝土梁的特点，本次分析时选用Solid65混凝土单元模拟梁；选用Link8单元模拟预应力筋、非预应力筋及箍筋，其中，Solid65单元可以考虑混凝土的压碎和开裂，该单元有8个节点，每个节点有3个自由度：节点的X，Y，Z方向的线位移；单元具有分析拉应力区开裂和压应力区可能的压溃反应的能力，每个单元在8个积分点处进行开裂和压溃的检验。在单元的积分点处，一旦混凝土单元的主应力超出了混凝土的抗拉或抗压强度范围,单元则被标记为开裂或压溃,裂缝或压溃区的方向由相应的主应力方向确定。钢筋采用Link8空间杆元。

1.3材料的本构模型

本文混凝土采用von mises弹塑性随动强化本构模型，采用William-Warnker 5参数破坏准则，能够较好地反映混凝土在多轴受压复杂应力状态下的实际破坏情况。预应力钢绞线本文采用高强钢丝，采用3折线等向强化的本构关系，采用von Mises屈服准则以及等向强化的假定。

1.4有限元模型的建立及求解

模型为30 m预应力混凝土简支T梁[5-6]，结构尺寸布置见图1。由于结构和施加荷载的对称性，所以在建模时采用了1/2对称模型，全模型中共有90个预应力钢筋Link8单元，3 275个混凝土节点，1 824个混凝上Solid65单元，模型梁有限元模型第1载荷步为施加自重荷载和初始预应力；第2载荷步为施加2 900 kN的力，第2荷载步又包括290个荷载子步，程序每一级加载量为10 kN。在建模过程中为了取得较好的收敛解，模型选取0.2 m的网格尺寸自动划分网格划分后的有限元模型，见图2。对应的荷载-挠度计算结果见表1。

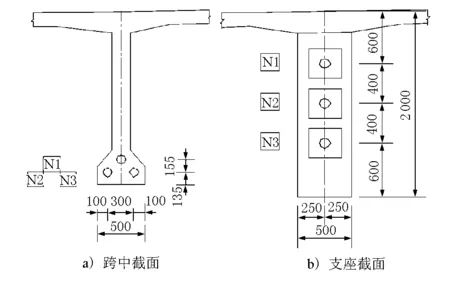
图1结构尺寸布置图(单位：mm)

图2　梁体有限元模型

数值荷载/kN010203040506070实际挠度/mm17.969.516.6793.710.543-2.39-5.42-8.338挠度增量/mm08.4511.2814.2517.4220.3523.3826.3数值荷载/kN808590100110120130140实际挠度/mm-12.7-14.8-19-25.8-32.9-38.3-48.8-50.5挠度增量/mm30.6632.7636.9643.7650.8656.2666.7668.46数值荷载/kN150160170180190200210220实际挠度/mm-56.811-63.007-69.325-75.848-82.253-88.93-95.098-101.4挠度增量/mm74.7780.9787.2993.81100.21106.89113.06119.36数值荷载/kN230240250260270280290实际挠度/mm-107.89-114.4-121.2-137.8-143.4-150.5-165挠度增量/mm125.85132.36139.16155.76161.36168.46182.96

由表1可见，预应力混凝土梁加载过程中，梁体跨中挠度变化可以分为开裂前弹性、裂后弹塑性和塑性3个阶段。第一阶段混凝土表现出面型的线弹性受力特征，说明，此阶段梁体的抗弯刚度没有变化，挠度荷载曲线为一条斜直线；之后一段时间内，表现为裂后弹塑性，挠度荷载曲线仍为一条斜直线，不过斜率较第一条直线斜率小，说明在一段时间内，梁体刚度比之前的线弹性小；第三阶段表现为从普通钢筋屈服到梁体破坏阶段，该阶段梁体表现为弹塑性阶段，荷载挠度曲线表现为斜率逐渐变小，表明梁体的刚度迅速减小。

2　计算结果分析

2.1外荷载与预应力筋应变的关系

设计原型梁采用ANSYS进行分析时，施加完预应力和自重荷载后，预应力筋跨中纯弯段的初始应力大小为1 300 MPa。取该时刻的状态为初始状态，计算每级荷载作用下预应力筋的应力总增量，并绘制外荷载作用下的模型梁跨中纯弯段预应力筋应力荷载曲线见图3。

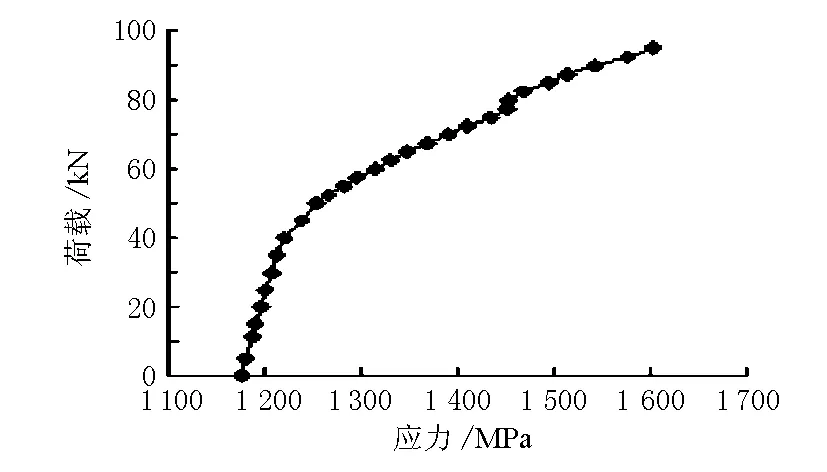
图3　预应力筋应力增量-荷载曲线

由图3可见，开裂前梁体处于线弹性阶段，跨中纯弯段预应力筋应力荷载曲线表现为一直线，在开裂荷载时，应力荷载曲线有一拐点，随后跨中纯弯段预应力筋应力荷载曲线仍能满足线性关系。

收稿日期：2015-06-10

DOI 10.3963/j.issn.1671-7570.2015.04.002