小世界网络中埃博拉病毒传播的研究

小世界网络中埃博拉病毒传播的研究

程静1,2，黄青1，谢铭杰1，吴小雨1，李佳君1，张志梁1，吕杰1,2

1上海医疗器械高等专科学校 医疗器械工程系(上海，200093)

2 上海健康医学院 医疗器械学院(上海，200093)

通信作者：吕杰，E-mail:lyj@smic.edn.cn

【摘要】目的为更好地防御和控制埃博拉病毒疫情，需要建立病毒在高度聚集的人类社会中的传播数学模型。方法建立了包含潜伏节点的小世界网络传播模型(SEIR模型)，并对病毒的实际传播情况进行了仿真，进而使用模型研究初始感染人数及社会的人群聚集度(关联度)对病毒传播过程的影响。结果模型的仿真结果与病毒实际报道的传播情况相符，表明所构建的模型对疫情防控具有现实指导意义。病毒的传播速度与初始染病人数和关联度具有明显的正相关关系，因此在潜伏期内对病毒传播进行干预以及对感染者进行隔离可对疫情进行有效控制。

【关键词】埃博拉病毒；传播；小世界网络；SEIR模型

doi:10.3969/j.issn.1674-1242.2015.02.007

作者简介：程静，E-mail:chengj@smic.edu.cn

【中图分类号】【文章标志码】A

文章编号：1674-1242(2015)02-0091-04

Abstract【】ObjectiveIn order to prevent and control Ebola virus disease, a new virus transmission model should be established.MethodsBased on the small-world network theory, a new SEIR model was proposed to simulate the transmission process of Ebola virus disease. Then, the number of infected and the frequency of human contacts, which were the two major factors, were investigated to explore their roles in virus transmission.ResultsSimulation results of the model were accorded with actual reports of the virus situation, which illustrated that the model was reasonable and practicable. There are positive relationships between propagation speed of the virus and these two major factors. Therefore, it is critical to isolate the infected and take some intervention methods in incubation period.

收稿日期：(2015-02-28)

Study on the Transmission of Ebola Virus in Small World Network

CHENG Jing, HUANG Qing, XIE Mingie, WU Xiaoyu, LI Jiajun, ZHANG Zhiliang, Lü Jie

1. Department of Medical Instrument Engineering,

Shanghai Medical Instrumentation College(Shanghai，200093)

2. Medical Instrument Department, Shanghai University of Medicine & Health Sciences(Shanghai，200093)

【Key words】Ebola virus, transmission, small-world network, SEIR mode

埃博拉(Ebola virus disease又称埃博拉出血热)是一种传播迅猛的急性致命传染疾病，致死率高达50%～90%[1]，埃博拉疫情在1976年刚果靠近埃博拉河流域的小村庄首次出现。近期从2013年起，该病毒在西非肆虐蔓延，始于几内亚，后蔓延至萨拉里昂、利比里亚及尼日利亚等国家，给人们的生命和财产带来巨大的损失，引起全球的广泛关注与思考[2]。对埃博拉病毒的传播过程进行数学模拟，可对其流行的影响因素进行分析，预测其爆发时间和规模，从而更好的改善应急机制，为疾病的防治提供理论依据和技术支持。

埃博拉病毒不同于其他流行病，其传播途径相对封闭，主要为直接接触病人的分泌物传播、注射传播和性接触传播[3-4]。目前国内外对于埃博拉病毒传播过程主要有增长动态模型[4]，SIR/SEIR等简单数学模型[5]；David N. Fisman等[4]使用衰变指数拟合模型(IDEA)来对病毒的传播过程进行模拟，虽然模拟结果与实际报道相符，但模型中所使用的参数的实际意义却难以精确定义；江华等[5]人使用SIR模型来模拟埃博拉病毒的传播，但其研究只局限于简单的数学模型分析，并没有考虑埃博拉病毒在不同的社会人际网络中的传播能力，以及潜伏期感染人数对其传播速度产生的影响。由Watts等[6-7]提出的小世界网络模型，人群通常是高度聚集的，并以一定的概率随机混合在一起，是一种可以用来描述复杂社会拓扑结构的理想模型。本文根据埃博拉病毒的传播特点，在小世界网络理论基础上，建立了包含潜伏节点的埃博拉病毒传播模型，并结合实际数据，考察了模型的实际应用性能。进而探索了初始染病人数、传播人群接触关系等因素对病毒传播的影响，为埃博拉病毒疫情的防御和控制提供了理论依据和现实指导。

1　埃博拉病毒传播模型

1.1模型假设

假设人群模型分为4类群体，即易感者群体、潜伏者群体、感染者群体与移除者群体。易感者与感染者无防护的接触将导致传染；易感者与感染者是同质混合的，潜伏期内不具有传染；在埃博拉病毒传播过程中不采取任何干预措施；不考虑人口的迁出和迁入，也不考虑人口自然状态下的出生和死亡。

1.2模型结构

图1埃博拉病毒传播模型结构示意图

Fig.1Transsmission model of Ebola virus

埃博拉病毒传播模型结构示意如1图所示。S表示易感者，即未感染埃博拉病毒人群；E表示潜伏者，即携带埃博拉病毒但无感染症状，即处于潜伏期的人群，不具有传染性；I表示感染者，即存在埃博拉病毒感染症状并且具有传染性的人群；R表示移除者，即死亡人群。在疾病传播过程中，易感者与感染者接触后，以一定的概率P转化为潜伏者；α表示单位时间内潜伏者向感染者转变的数目；β表示单位时间内感染者向移出者转变的数目；T1表示由潜伏者到感染者所需的平均时间；T2表示感染者到移除者所需的平均时间。N表示总人口数，即易感者、潜伏者、感染者与移除者之和。根据埃博拉病毒2013～2014年在西非爆发的实际数据[8-9]，可知α、β为极限概率趋近于1 的两个变量，T1为2～20 d，T2为7 d；研究中通过对实际数据的拟合，采用最小平方法获得传播概率P。

1.3模型的实现

本文各种模拟和绘图使用Matlab程序进行编写。根据小世界网络模型理论，如图2所示：定义每一个节点为一个个体的人，其中空心圆为易感者(S)，实心圆为感染者(I)，空心方块为潜伏者(E)，实心方块移除者(R)，网络节点总数代表总人口数；网络中的边表示节点之间存在联系即两个个体之间存在着接触，网络中每个节点与其他节点的平均连接数定义为关联度。在模型中，我们假设总人口数不发生改变，即整个网络不会有新的节点进入，总人口数设为10 000。在进行模拟时，以一定的概率随机地变动网络中的每条边，即边的一个端点保持不变，然后随机选择网络中的节点作为另一个端点。同时限定，任意两个不同的节点之间最多只能存在一条边，每一个节点不存在边与自身相连。在小世界网络中，寻找感染者的邻居节点，并判断邻居节点的属性，如果邻居节点属于易感者，则他们将以一定的概率P发生病毒感染；如果是感染者、潜伏者、或者移除者，则不发生疾病感染。当节点从未感染状态(S)到潜伏状态(E)时，时间属性开始计数，在遍历节点时判断其时间属性是否大于T1，符合时则将该节点转变为感染者(I)。若节点已进入感染状态(I)，其新的时间属性开始计数，在遍历节点时判断其时间属性是否大于T2，符合时则将该节点转变为移除者，属性为死亡(D)，节点从网络中去除，不再参与人群传染过程。模型的算法流程如图3所示。

图2小世界网络模型

Fig.2Structure of small world network model

空心圆为易感者(S)，实心圆为感染者(I)，

空心方块为潜伏者(E)，实心方块点为移除者(R)

图3算法流程图

Fig.3Flow diagram of Ebola virus transmission model

2　结果与讨论

在研究中，我们进行了以下的比较和模拟研究：首先，将模型对埃博拉病毒传播过程的模拟结果与1976年在刚果爆发的疫情数据作比较，考察模型对真实情况的模拟效果；其次，固定社会网络中的人群关联度不变，改变初始感染人数，研究其对病毒传播过程的影响。最后，我们固定初始染病人数，改变社会网络中的人群关联度，研究其对病毒传播过程的影响。

2.1埃博拉病毒模拟传播过程与实际情况的对比

为了验证我们的预测模型的准确性，我们模拟了埃博拉病毒发病人数占总人口的百分比随时间的变化情况。在模拟时，我们设定初始染病人数为1人，社会网络中人群的关联度为50(图4)，模拟结果表明病毒发病高峰期出现在第35～40 d，死亡率约为91%。据报道，1976年在刚果爆发的埃博拉病毒疫情中，疫情的高峰期出现在第35 d[9-10]，死亡率90%，与我们的模拟数据基本吻合。该结果表明，我们所建立的模型能够逼真地模拟病毒的传播过程，可以为病毒传播的影响因素研究提供基础模型，进而为病毒的防御与控制提供理论依据。

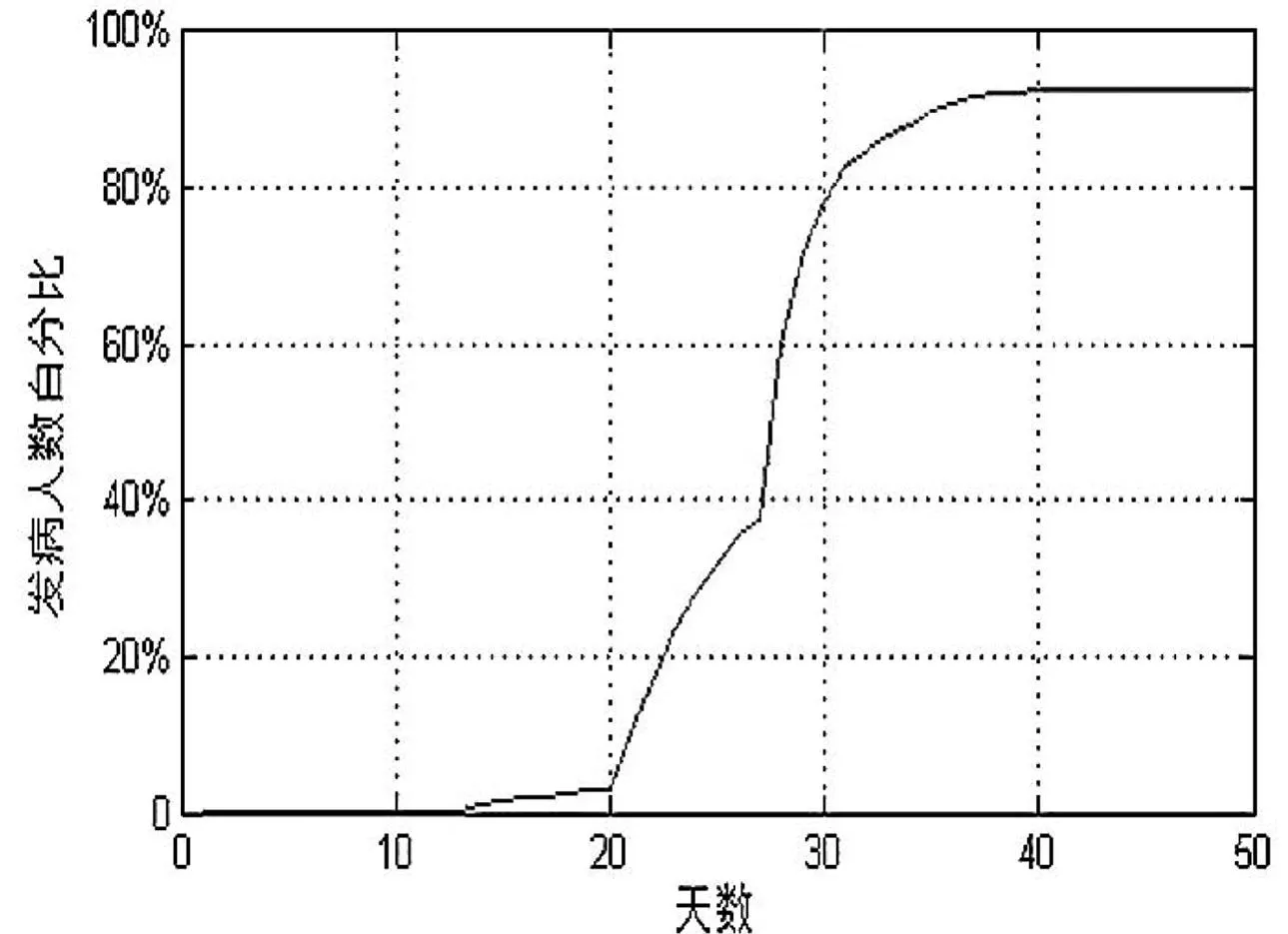
图4初始染病人数为1人、关联度为50时埃博拉病毒传播模拟结果

Fig.4Simulation results of Ebola virus transmission model with

initial infected number of 1 and correlation degree of 50

2.2初始染病人数对埃博拉病毒传播的影响分析

在实际工作中，我们研究了埃博拉病毒的传播曲线与初始染病人数之间的变化关系(设定网络中人口总数为10 000，人群的关联度为50)，如图5所示。在第1～15 d，染病者大多以潜伏状态存在，有症状的发病人数并没有显著增加；在第15～20 d出现了一波小规模的爆发，发病人数持续增长；在第20～30 d出现了大规模的爆发，发病人数快速增长；在第40 d左右发病人数占总人数的百分比接近90%，与报道的埃博拉的致死率相同[11-12]。当初始染病人数小于30人时，埃博拉病毒的传播曲线变化随初始染病人数的增加波动明显，初始染病人数越多，埃博拉病毒的传播速度增长越快。然而当初始染病人数大于30人时，埃博拉病毒的传播曲线变化随初始染病人数的增加波动并不明显，始终处在一种快速增长过程中。该研究结果表明，在埃博拉病毒疫情的初期，如果能够采取一些有效的干预措施，例如对感染者进行有效的治疗、密切观测潜伏者，将感染者控制在30人以下(占总人口比率为0.3%)，这将大大减缓病毒的传播速度，减轻病毒的爆发规模。

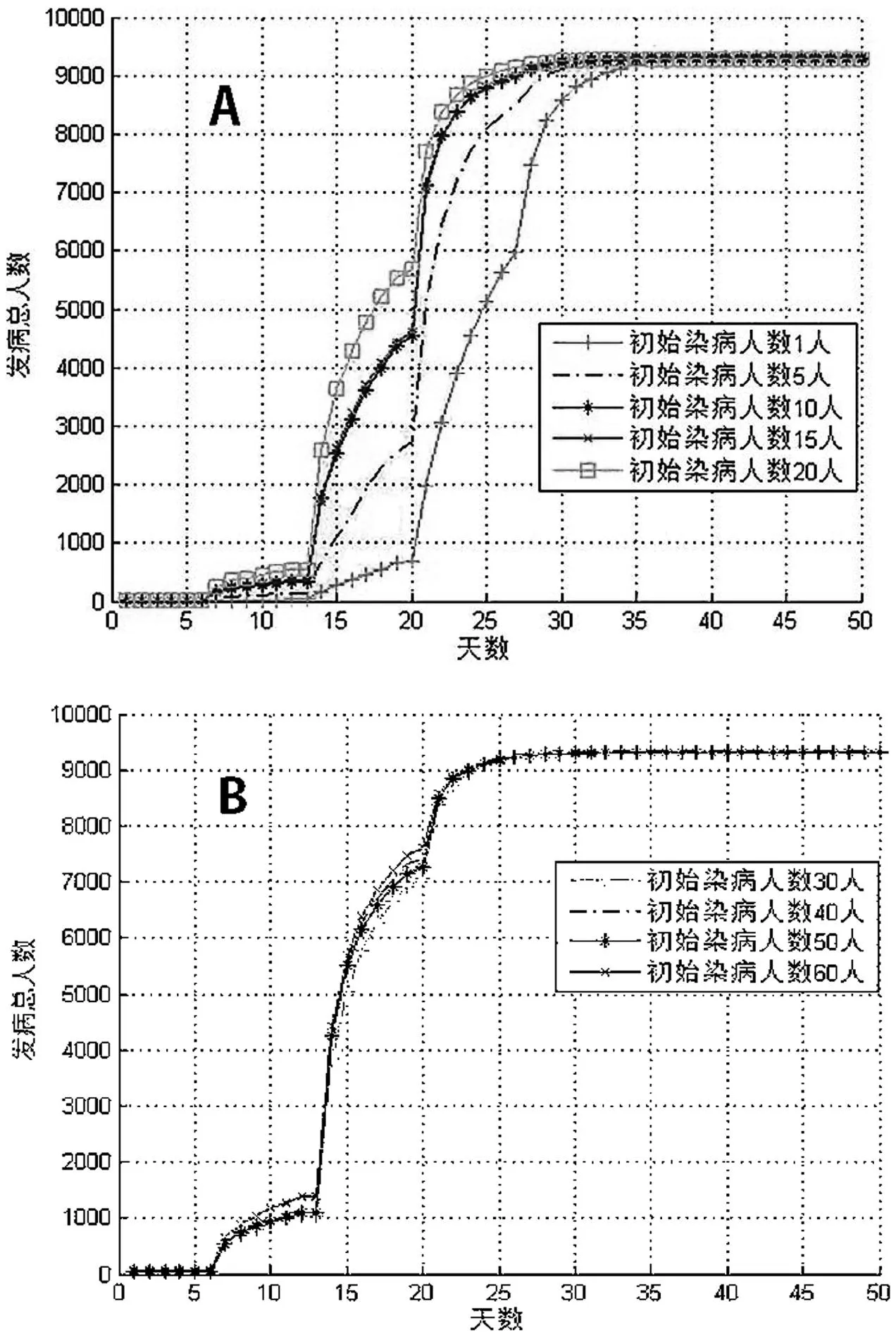
图5关联度为50，的埃博拉病毒传播模拟曲线

(A)初始染病人数为1～20人；(B)初始染病人数为30～60人

Fig.5Simulation results of Ebola virus transmission model with

correlation degree of 50 (A) initial infected number varied from

1 to 20;(B)initial infected number varied from 30 to 60

2.3关联度对埃博拉病毒传播的影响分析

为考察感染者的社会关系对埃博拉病毒传播的影响，我们研究了埃博拉病毒的传播曲线变化与关联度之间的关系(设定初始染病人数为10人，关联度的变化范围为20～60)。在研究中，我们假定网络中不同类的节点具有不同的网络属性，同一类节点具有不同的权重，来模拟每个节点代表的个体在社会中角色的不同，其社会活跃程度的不同 (模拟的结果见图6)。如图6所示，埃博拉病毒的传播速度与关联度成正相关关系，随着社会中人群的关联度的快速增长，埃博拉病毒的传播速度也逐渐增快。由此可知，感染者的社会关系对埃博拉病毒的传播具有重要影响，因此发现埃博拉病毒疫情后，需要采取切实的干预措施，例如医学隔离感染者、对感染者的接触人群进行跟踪观测等，这将有效地降低感染者的社会关联度，将疫情控制在一定的范围内，并为病毒的防控赢得时间，大大减缓病毒的传播。

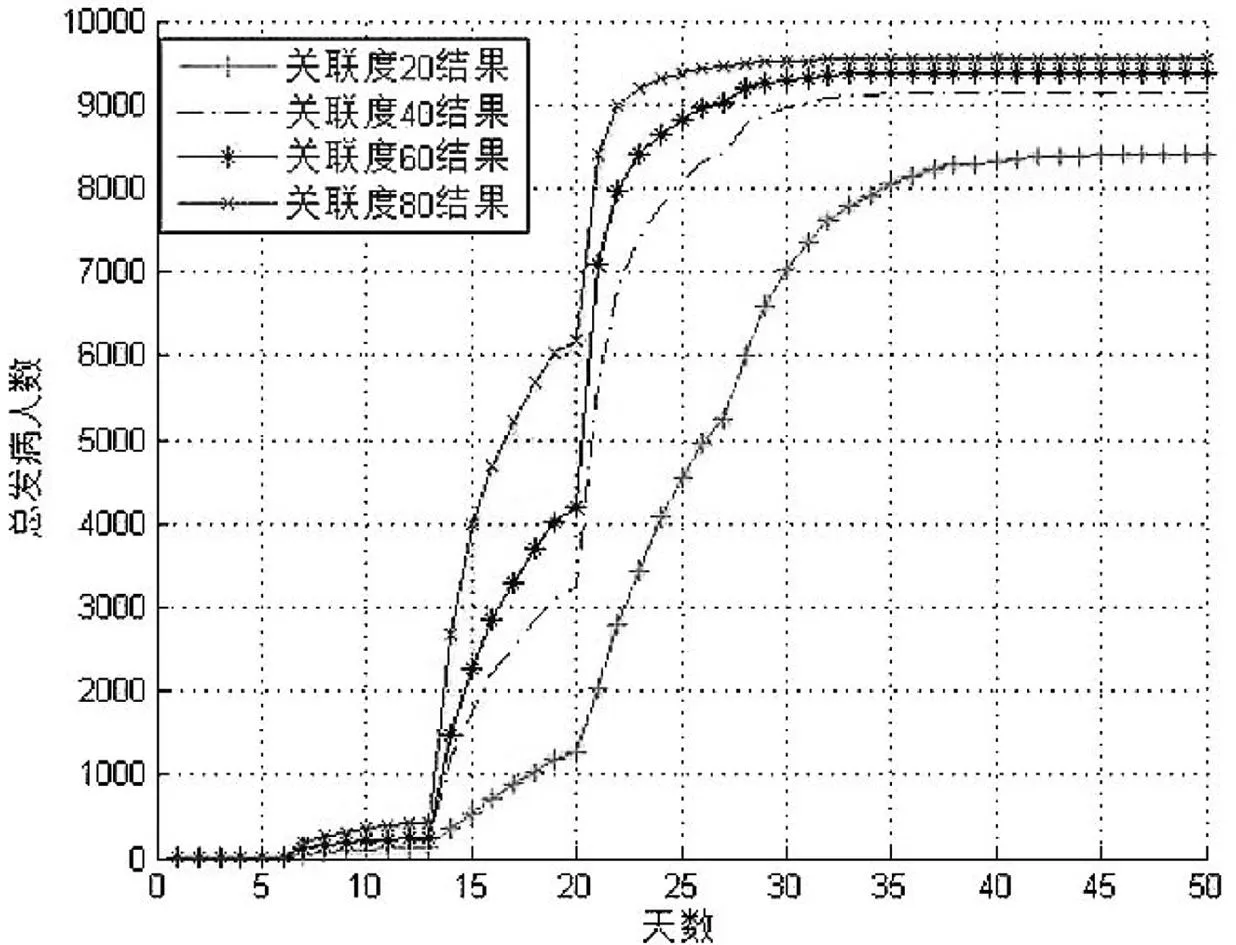
图6初始染病人数为10人，不同关联度下，

埃博拉病毒传播模拟曲线

Fig.6Simulation results of Ebora virus transmission

model when initial infected number is 10 with

different correlation degree

3　结论

在研究中，我们首先建立了包含潜伏节点的小世界网络传播模型，来模拟埃博拉病毒在人类社会中的传播过程，模型模拟的结果与1976年刚果爆发的埃博拉疫情数据基本吻合，表明所构建的模型是合理的，具有实际指导意义。在此基础上，我们研究了初始感染人数以及社会中人群的关联度与病毒的传播关系，结果表明这两个因素与疫情的发展具有明显的正相关关系，因此在疫情的早期，采取对感染者进行隔离和积极治疗，并且密切追踪感染者的接触人群等措施可以有效控制疫情的发展，极大地减少病毒对人们的生命和财产带来的损失。

参考文献

[1] Gire SK, Goba A, Anderson KG, et al. Genomic surveillance elucidates Ebola virus origin and transmission during the 2014 outbreak[J]. Science, 2014，345(6202): 1369-1372.

[2] Briand S, Bertherat E, Cox P, et al. The international Ebola emergency[J]. N Engl J Med，2014,371:1180-1183.

[3] Baron RC, McCormick JB, Zubeir OA, Ebola virus disease in southern Sudan: hospital dissemination and intrafamilial spread[J]. Bull World Health Organ,1983, 61(6): 997-1003.

[4] Chowell G, Viboud C, Hyman JM, et al.The Western Africa Ebola virus disease epidemic exhibits both global exponential and local polynomial growth rates[J]. PLOS Currents Outbreaks, 2015, arXiv:1411.7364 [q-bio.PE].

[5] 江华, 潘海霞. 基于计算机流行病学的埃博拉出血热传播与爆发仿真研究[J]. 中华急诊医学杂志, 2014, 23(9): 974-978.

[6] Watts DJ,Strogatz SH.Collective dynamics of 'small-world'networks[J]. Nature,1998,393(4): 440-442.

[7] 谢莉, 姚伟. 复杂网络中男-男同性性行为间的艾滋病传播[J]. 科学通报, 2013,58(18):1731-1738.

[8] Francesconi P, Yoti Z, Declich S, et al. Ebola hemorrhagic fever transmission and risk factors of contacts, Uganda[J]. Emerg Infect Dis,2003,9(11):1430-1437.

[9] WHO Ebola Response Team. Ebola virus disease in west africa - The first 9 months of the epidemic and forward projections[J]. N Engl J Med, 2014, 371(16):1481-1495.

[10] Chowell G, Nishiura H. Transmission dynamics and control of Ebola virus disease(EVD):a review[J]. BMC Medicine, 2014,12:196-212.

[11] Gatherer D. An introduction to Ebola: the virus and the disease[J]. General Virol,2014,95(8):1619-1624.

[12] Pourrut X, Kumulungui B, Wittmann B, et al. The natural history of Ebola virus in Africa[J]. Microbe Infect, 2005,7(8):1005-1014.