活性粉末混凝土柱恢复力模型试验研究
王德弘,鞠彦忠,郑文忠
活性粉末混凝土柱恢复力模型试验研究
王德弘1, 2,鞠彦忠1,郑文忠2
(1. 东北电力大学建筑工程学院,吉林吉林,132012;2. 哈尔滨工业大学土木工程学院,黑龙江哈尔滨,150090)
进行18个活性粉末混凝土(RPC)配筋柱的低周反复加载试验,研究轴压比、纵筋配筋率和配箍率等对活性粉末混凝土配筋柱强度、刚度和滞回特性的影响规律,通过理论分析和对试验结果的回归分析,建立活性粉末混凝土配筋柱的三线型恢复力模型,并给出各特征点参数的计算方法。研究结果表明:该恢复力模型能够反映轴压比、纵筋配筋率和配箍率对滞回特性的影响,与试验结果吻合较好,可为活性粉末混凝土结构的非线性动力分析提供参考,为活性粉末混凝土柱类构件的抗震设计提供参考。
活性粉末混凝土;框架柱;恢复力模型;骨架曲线;滞回特性
随着电子结构分析中计算机的广泛应用,结构的弹塑性时程动力分析方法已经成为建筑结构抗震分析及设计的一种重要方法。而一个合理的恢复力模型是动力分析结果可信度的基础[1−2]。国内外学者对普通混凝土和高强混凝土构件的滞回特性进行了大量的试验研究,提出了多种恢复力模型[3−9]。但是,活性粉末混凝土(reactive powder concrete,RPC)是一种超高强度超高性能的新型水泥基复合材料。考虑到RPC结构材料及构件变形性能的特殊性,以往的这些研究成果并不能完全适用于RPC结构或构件的抗震分析,因此,对活性粉末混凝土构件的恢复力模型进行研究具有重要的实际意义。郝文秀等[10]对5个RPC空心桥墩试件进行了无轴压的低周反复荷载试验,对试件的破坏形态、滞回特性和延性性能进行了研究。在对桥墩试件骨架曲线特点进行分析的基础上建立了RPC空心桥墩的退化双线性恢复力模型。黄明兰[11]采用有限元软件模拟了4种工况下RPC配筋柱的滞回耗能性能、骨架曲线及恢复力模型,分析了轴压比和配筋率对RPC配筋柱恢复力特性的影响。王诚等[12−13]通过对3个RPC箱型墩试件拟静力试验,研究了常轴力作用下水平荷载作用方向对RPC箱型墩抗震性能的影响,分析了各试件的滞回曲线和骨架曲线的特征,建立了RPC箱型桥墩的恢复力模型。目前对于RPC柱类构件的恢复力特性研究已取得了一定的成果,但是由于试验数据非常有限,考虑的影响因素较少,因此,现有的恢复力模型的适用性有限。本文作者通过对18个大比例尺RPC配筋柱进行拟静力试验,研究轴压比、纵筋配筋率、配箍率等设计参数对RPC配筋柱恢复力特性的影响。在对试验结果分析的基础上,考虑影响恢复力模型的主要因素,建立适合于RPC配筋柱恢复力特性的三线型恢复力模型。
1 试验概况
1.1 试件设计
本试验共设计18个试件,试验柱有效高度为 1 500 mm,试件截面尺寸及配筋形式如图1所示,保护层厚度取15 mm。图1中表示牌号HRB335钢筋;表示牌号HPB235钢筋。试件设计考虑轴压比、纵筋配筋率、配箍率及钢纤维体积分数4个影响因素,试件主要参数如表1所示。试件纵筋采用HRB335热轧钢筋,箍筋采用HPB235钢筋[14]。钢纤维为高强钢丝切断型细圆形表面镀铜钢纤维,其直径为0.2~0.3 mm,长度为13~15 mm。
1.2 试验装置与加载方案
试验加载装置如图2所示,竖向荷载由1 000 kN数控电动液压伺服作动器通过滚轴支座施加于柱顶,水平荷载通过固定在反力墙上的500 kN数控电动液压伺服作动器施加。试验采用荷载、位移混合控制的加载制度。试件屈服前采用荷载控制的方式,屈服后按照位移控制的方式进行加载[15]。试验加载制度示意图如图3所示。
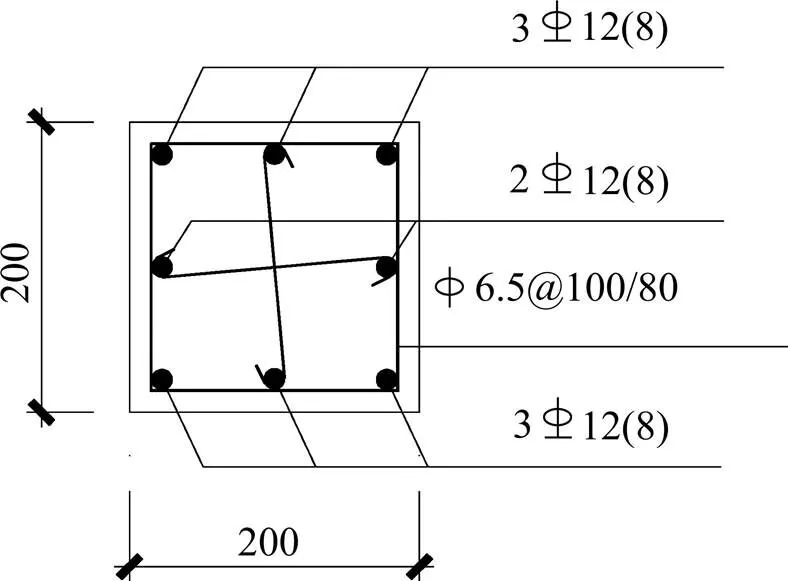
单位:mm
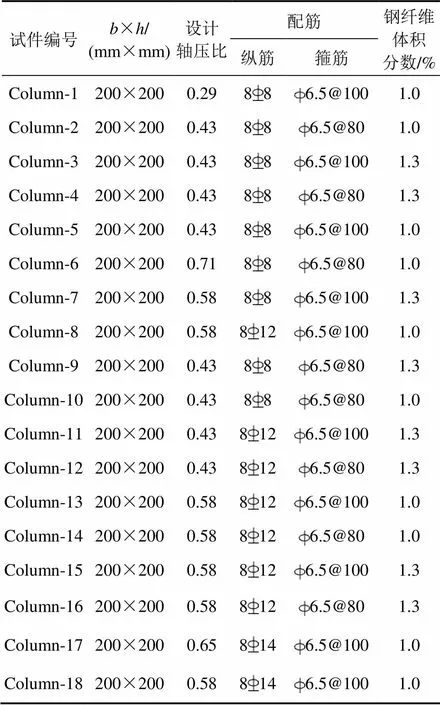
表1 试件参数
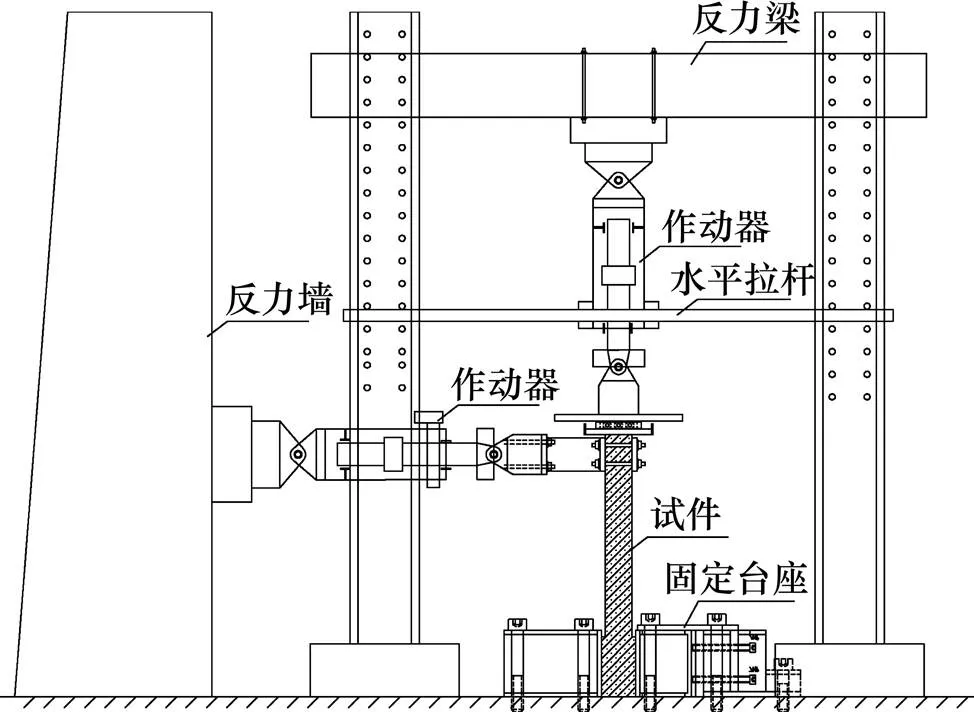
图2 试验加载装置图
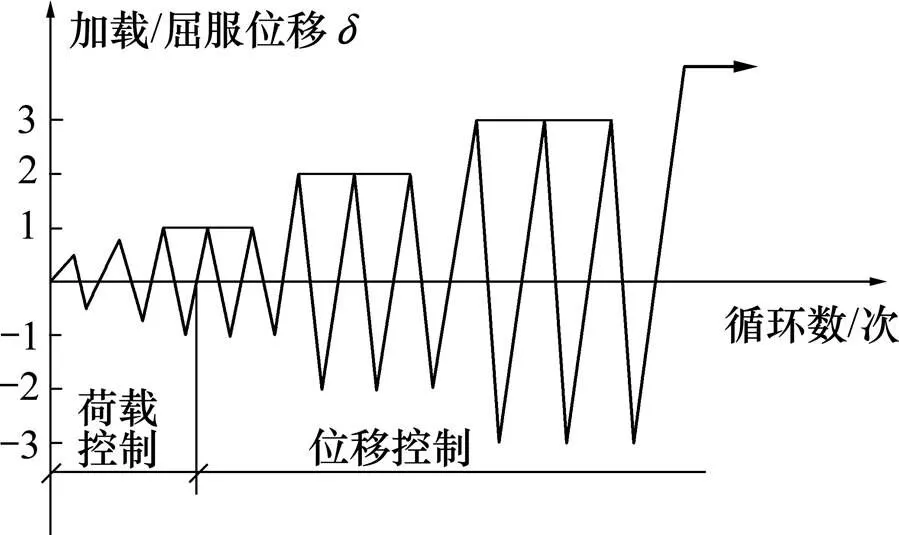
图3 试验加载制度示意图
2 试验结果与分析
2.1 典型滞回曲线特征
图4所示为活性粉末混凝土配筋柱典型的柱顶荷载−位移滞回曲线。从图4可以发现活性粉末混凝土柱的滞回曲线具有以下几个特点。
1) 在试验加载初期,试验柱的卸载刚度与初始的加载刚度基本相等,呈现出线性卸载特征。当达到屈服荷载后,随着加载位移的增加,滞回曲线出现加载和卸载刚度的衰减现象,但衰减幅度不大,此时滞回曲线为较小的梭形。当加载位移幅值继续增加,加载和卸载刚度的衰减明显加快,此时滞回环出现不同程度的捏拢现象,试件的滞回曲线均呈现为弓形曲线。
2) 当达到最大侧向承载力后,柱顶水平荷载逐渐降低,出现下降段。试件柱的塑性变形能力表现出明显的降低趋势,呈现出刚度退化现象,且刚度退化随轴压比的增大而更加明显。
3) 轴压比和纵筋配筋率对活性粉末混凝土配筋柱的滞回特性存在明显的影响。比较试件Column-11与Column-15,Column-12与Column-16滞回曲线可知:低轴压比的试件的滞回曲线更为饱满,其延性和能量耗散能力更好。从试件Column-9与Column-12,Column-8与Column-18滞回曲线的比较可以看出:随着纵筋配筋率的提高,试验柱的滞回曲线更加饱满,延性性能及耗能能力均有较大程度的提高。
4) 从试件Column-11与Column-12,Column-15与Column-16滞回曲线的比较可以看出:配箍率对活性粉末混凝土配筋柱的滞回特性影响不大。但在高轴压比条件下,配箍率的提高能够在一定程度上减缓试件在大变形时的强度退化,该规律与高轴压普通混凝土柱的试验结果[6]一致。
2.2 骨架曲线
图5所示为部分试件的荷载−位移骨架曲线。从图5可以看出活性粉末混凝土配筋柱的骨架曲线具有以下几个特点。
1) 荷载−位移骨架曲线关于原点对称性较好。
2) 荷载−位移骨架曲线的两侧明显地表现出弹性阶段、强化阶段和强度退化阶段。
3) 到达侧向极限承载力后,荷载−位移骨架曲线的曲线下降速度比较缓慢,并且存在1个较长的强度下降平台,说明活性粉末混凝土配筋柱延性较好。
表2所示为活性粉末混凝土配筋柱骨架曲线主要特征点试验结果。表2中y和y分别为屈服荷载和屈服位移;m和m分别为最大荷载和最大荷载所对应的位移;u和u分别为极限荷载和极限位移。从表2可以看出:轴压比的增大和纵筋配筋率的增加能够显著提高试件的侧向承载力,提高幅度可以达到34%。配箍率的提高在一定程度上改善了荷载达到峰值后阶段的滞回特性,使骨架曲线的下降段变得较为平缓。
3 恢复力模型
3.1 骨架曲线
活性粉末混凝土配筋柱的荷载−位移骨架曲线可以大致分为弹性段、弹塑性段及下降段3部分,考虑在结构弹塑性地震反应分析及工程应用中的方便,在反映试件的滞回特征的前提下,将该恢复力模型要尽可能地简化[6]。根据试件的骨架曲线特征,将活性粉末混凝土配筋柱的骨架曲线简化为三折线,简化的骨架曲线模型如图6所示。该模型具有3个特征点,分别对应屈服点,最大荷载点和破坏点。确定骨架曲线模型需要9个特征点参数:弹性阶段的刚度1、屈服后的刚度2、下降段的刚度3、屈服荷载y、屈服位移y、最大荷载m、最大荷载所对应的位移m、极限荷载u和极限位移u。

试件:(a) Column-7; (b) Column-8; (c) Column-9; (d) Column-11; (e) Column-12; (f) Column-15; (g) Column-16; (h) Column-18

1—Column-1 (轴压比n=0.29); 2—Column-7 (n=0.58); 3—Column-9 (n=0.43); 4—Column-11 (n=0.43); 5—Column-15 (n=0.58)
影响钢筋混凝土柱的强度、刚度的因素很多,活性粉末混凝土配筋柱与其相似,本文仅考察轴压比、纵筋配筋率、配箍率和钢纤维体积分数4个因素的影响。因此,本文主要依据轴压比、纵筋配筋率、配箍率sv和钢纤维体积分数这4个因素建立恢复力 模型。

表2 骨架曲线主要特征点试验结果

图6 骨架曲线模型
1) 活性粉末混凝土试件柱屈服前,将其恢复力模型骨架曲线简化为连接原点和屈服点的直线段,其斜率即为弹性阶段的刚度1,按下式确定:
其中:
式中:y为柱截面的屈服弯矩;y为柱截面的屈服曲率,可以由正截面分析得到。
2) 活性粉末混凝土试件柱屈服后,将其恢复力模型骨架曲线简化为连接屈服点和最大荷载对应点的直线段。通过对试验结果的分析,最大荷载与屈服荷载的比值随着轴压比和纵筋配筋率的增加而增加,随着体积配箍率的增加而减小。通过对试验数据的拟合得到其关系表达式为
式中:为轴压比;为纵筋配筋率;sv为体积配箍率。而最大荷载对应的位移与屈服位移的关系表达式为
3) 试件屈服后的刚度为
4) 根据JGJ 101—96“建筑抗震试验方法规程”[15],试件的极限荷载为最大荷载的0.85倍,即
5) 极限位移为
6) 达到最大荷载后,骨架曲线进入下降段,下降段的刚度3=1,为刚度退化系数,通过对试验结果的回归分析拟合,得到刚度退化系数为
又因为
所以,此活性粉末混凝土配筋柱的恢复力模型骨架曲线的9个特征点参数均可求得。
3.2 卸载刚度
试验结果表明,加载位移幅值是影响卸载刚度最主要的因素,按照卸载刚度确定方法[16−17]统计计算不同阶段RPC试件柱的卸载刚度,并对统计结果进行回归分析可以得到RPC试件柱的卸载刚度与弹性阶段刚度1的关系为
式中:u为卸载刚度;u为卸载点对应的位移。
图7所示为刚度比u/1、位移比u/y的试验统计结果与拟合得到的计算曲线。从图7可知:该拟合曲线与试验结果吻合较好,说明该计算公式具有较高的精度。

图7 刚度退化拟合
3.3 滞回规则
图8所示为活性粉末混凝土配筋柱的恢复力模型,其中为图6中的荷载−位移骨架曲线,关于原点与对称,其滞回规则为:
1) 试件承受的水平荷载在未超过屈服强度时,构件处于弹性阶段,加载和卸载均沿着骨架曲线的弹性段()进行,不考虑刚度退化和残余变形。
2) 试件承受的荷载超过屈服强度后,但未达到最大荷载时,构件处于弹塑性阶段,加载沿着骨架曲线进行,加载刚度为屈服后的刚度2。此时卸载,即卸载点为图8所示的点,其卸载刚度按照式(11)确定。
3) 荷载超过最大荷载后,进入下降段,加载刚度取骨架曲线下降段刚度3。此时的卸载刚度也按式(11)计算。
4) 当进行反向加载时,若反向经历过的最大位移未超过屈服位移,则从零荷载点(图8所示的点)处直接指向反向屈服点′,当反向经历过的最大位移超过屈服位移时,从零荷载点处直接指向反向经历过的最大位移点;反向卸载后再正向加载时,从零荷载点处直接指向正向经历过的最大位移点。

图8 活性粉末混凝土配筋柱的恢复力模型
3.4 计算结果与试验结果比较
图9所示为部分试件骨架曲线的计算结果与试验结果的比较。从图9可以看出:恢复力模型骨架曲线计算结果与试验结果较为接近,表明本文提出的三线型恢复力模型能够较好的反映RPC配筋柱的滞回特性。
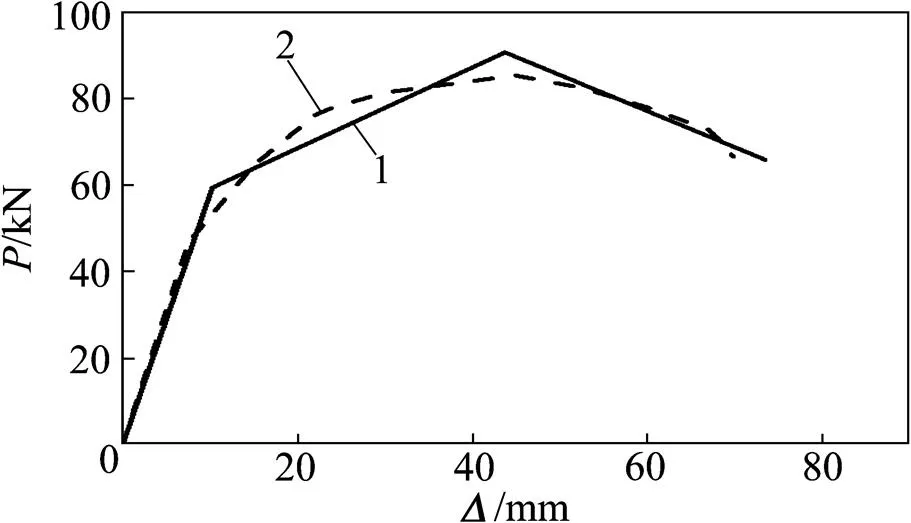
1—计算结果;2—实验结果
4 结论
1) 试件柱的纵筋配筋率及配箍率对活性粉末混凝土配筋柱的滞回特性存在明显的影响。随着纵筋配筋率及配箍率的提高,试验柱的滞回曲线更加饱 满,延性性能及耗能能力均有一定的提高。轴压比和纵筋配筋率对试件的侧向承载力影响显著,轴压比的增大和纵筋配筋率的增加能够显著提高试件的侧向承 载力。
2) 通过对试验结果进行多元线性拟合,确定了恢复力模型参数与轴压比、配筋率和配箍率的关系,给出了恢复力模型特征点参数的计算方法及相关的计算公式,计算方法简单实用。
3) 本文提出的RPC配筋柱的三线型恢复力模型与试验结果吻合较好,具有较高的精度,可为RPC结构的弹塑性动力分析提供参考。
[1] 张国军, 吕西林, 刘伯权. 高强混凝土框架柱的恢复力模型研究[J]. 工程力学, 2007, 24(3): 83−89. ZHANG Guojun, LÜ Xilin, LIU Boquan. Study on resilience models of high-strength concrete frame columns[J]. Engineering Mechanics, 2007, 24(3): 83−89
[2] 张国军, 吕西林, 刘伯权. 轴压比超限时框架柱的恢复力模型研究[J]. 建筑结构学报, 2006, 27(1): 90−98. ZHANG Guojun, LÜ Xilin, LIU Boquan. Research on restoring force model of frame columns with ultra-limited axial compression ratio[J]. Journal of Building Structures, 2006, 27(1): 90−98.
[3] Clough R W, Johnston S B. Effect of stiffness degradation on earthquake ductility requirements[C]// Proceedings of the 2nd Japan Earthquak Engineering Symposium, Tokyo: JSCE, 1966: 37−44
[4] Takeda T, Sozen M A, Nielson N N. Reinforced concrete response to simulated earthquakes[J]. Journal of Structural Division, ASCE, 1970, 96(12): 2557−2573.
[5] Saiidi M. Hysteresis models for reinforced concrete[J]. Journal of Structural Division, ASCE, 1982, 108(5): 1077−1087.
[6] 郭子雄, 吕西林. 高轴压比框架柱恢复力模型试验研究[J]. 土木工程学报, 2004, 37(5): 32−38. GUO Zixiong, LÜ Xilin, Experimental study on the hysteretic model of RC columns with high axial compression ratio[J]. China Civil Engineering Journal, 2004, 37(5): 32−38.
[7] 马颖, 张勤, 贡金鑫. 钢筋混凝土柱弯剪破坏恢复力模型骨架曲线[J]. 建筑结构学报, 2012, 33(10): 116−125. MA Ying, ZHANG Qin, GONG Jinxin. Skeleton curves of restoring force model of reinforced concrete columns failed in flexure-shear[J]. Journal of Building Structures, 2012, 33(10): 116−125.
[8] 齐岳, 郑文忠. 核心高强混凝土柱荷载−位移恢复力模型[J]. 哈尔滨工业大学学报, 2010, 42(4): 531−535. QI Yue, ZHENG Wenzhong. Restoring-force model of load versus displacement for concrete columns with high strength Core[J]. Journal of Harbin Institute of Technology, 2010, 42(4): 531−535.
[9] 马恺泽, 梁兴文, 李斌. 方钢管高强混凝土柱恢复力模型研究[J]. 世界地震工程, 2011, 27(1): 54−59. MA Kaize, LIANG Xingwen, LI Bin. Research on the restoring force model of high strength concrete-filled rectangular steel tubular columns[J]. World Earthquake Engineering, 2011, 27(1): 54−59.
[10] 郝文秀, 钟铁毅, 赵冠远. 活性粉末混凝土空心桥墩恢复力模型试验研究[J]. 铁道学报, 2011, 33(1): 89−93. HAO Wenxiu, ZHONG Tieyi, ZHAO Guanyuan. Experimental study on the restoring force model of reactive powder concrete hollow piers[J]. Journal of the China Railway Society, 2011, 33(1): 89−93.
[11] 黄明兰. 活性粉末混凝土配筋柱滞回性能数值模拟[D]. 北京: 北京交通大学土木建筑学院, 2011: 44−59. HUANG Minglan. Simulation on hysteretic behavior of reactive powder concrete reinforced columns[D]. Beijing: Beijing Jiaotong University. School of Civil Engineering, 2011: 44−59.
[12] 王诚. 活性粉末混凝土箱型桥墩抗震性能试验研究[D]. 长沙: 湖南大学土木工程学院, 2010: 32−37. WANG Cheng. Experimental study on seismic performance of RPC box piers[D]. Changsha: Hunan University. College of Civil Engineering, 2010: 32−37.
[13] 任亮, 方志, 王诚. 考虑双轴水平力耦合效应的RPC箱型桥墩恢复力模型试验研究[J]. 地震工程与工程振动, 2012, 32(2): 152−159. REN Liang, FANG Zhi, WANG Cheng. Experimental study on the restoring force model of reactive powder concrete box piers under biaxial horizontal loads[J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(2): 152−159.
[14] 鞠彦忠, 王德弘, 白俊峰. 活性粉末混凝柱抗震性能的试验[J]. 哈尔滨工业大学学报, 2013, 45(8): 111−116. JU Yanzhong, WANG Dehong, BAI Junfeng. Seismic performance of reactive powder concrete columns[J]. Journal of Harbin Institute of Technology, 2013, 45(8): 111−116.
[15] JGJ 101—96, 建筑抗震试验方法规程[S]. JGJ 101—96, Specification of testing methods for earthquake resistant building[S].
[16] Watson S, Zahn F A, Park R. Confined reinforcement for concrete columns[J]. Journal of Structural Engineering, 1994, 120(6): 1798−1824.
[17] Watson S, Park R. Simulated seismic load tests on reinforced concrete columns[J]. Journal of Structural Engineering, 1994, 120(6): 1825−1849.
(编辑 罗金花)
Experimental study on restoring force model of reinforced reactive powder concrete columns
WANG Dehong1, 2, JU Yanzhong1, ZHENG Wenzhong2
(1. School of Civil Engineering and Architecture, Northeast Dianli University, Jilin 132012, China;2. School of Civil Engineering,Harbin Institute of Technology, Harbin 150090, China)
Cyclic loading tests of 18 reinforced reactive powder concrete (RPC) columns were conducted, the effects of axial compression ratio, longitudinal reinforcement ratio and stirrup ratio on strength, rigidity and hysteretic characteristics were discussed. Through theory analysis and regressive analysis of experimental results, a three-line restoring force model was proposed, and calculation method was presented. The results show that the proposed restoring force model reflects the effect of axial compression ratio, longitudinal reinforcement ratio and stirrup ratio on the hysteretic characteristics of reinforced reactive powder concrete columns, which fits in well with the experimental results of reinforced reactive powder concrete columns. The proposed restoring force model can be used for the nonlinear analysis of reinforced reactive powder concrete structures, which can be referenced to in the designing of RPC columns.
reactive powder concrete; frame columns; restoring force model; skeleton curve; hysteretic characteristics
10.11817/j.issn.1672-7207.2015.09.039
U442.5+5;TU528.572
A
1672−7207(2015)09−3454−07
2014−12−27;
2015−02−28
国家自然科学基金资助项目(50878040);国家教育部长江学者奖励计划项目(2009-37) (Project(50878040) supported by the National Natural Science Foundation of China; Project(2009-37) supported by Changjiang Scholars Program of China)
鞠彦忠,博士,教授,从事高性能混凝土材料研究;E-mail: juyanzhong@126.com

