基于双边滤波算法的树木点云模型去噪方法研究

管西鹏，陈宇拓，张怀清 ，刘 闽，李永亮

（1.中南林业科技大学 计算机与信息工程学院，湖南 长沙 410004；2.中国林业科学研究院 资源信息所，北京 100091）

基于双边滤波算法的树木点云模型去噪方法研究

管西鹏1，陈宇拓1，张怀清2，刘 闽2，李永亮2

（1.中南林业科技大学 计算机与信息工程学院，湖南 长沙 410004；2.中国林业科学研究院 资源信息所，北京 100091）

针对三维激光扫描仪获取的树木点云数据存在噪声点的问题，结合双边滤波算法，通过设定空间邻近度因子σc值不变、灰度邻近度因子σs变化以及σs值不变、σc变化的2种不同参数取值状态，根据计算得到的双边滤波权因子α，选择剔除部分与当前采样点距离过大的相邻采样点，更新所有的数据点，最后得到经过滤波后的新数据点。经过对比分析2种参数取值状态下的不同去噪结果，可得到合理的参数取值，进而实现对树木点云模型去噪的处理，且达到保持原特征的目的。最后选取2个合适的实验数据模型，进一步对实验结果进行验证。实验结果表明该算法简单高效，噪声去除效果良好，具有较好的实用性和研究意义。

树木测量；双边滤波算法；点云去噪；空间邻近；灰度邻近

三维激光扫描仪通过激光测距方法对真实物体进行测量，使得待扫描的真实物体的三维数据获取变得简单可靠[1]。随着三维扫描技术和林业可视化技术的发展，根据激光扫描获取真实树木的高精度点云数据信息，对获取的点云数据进行三维重建，得到更加真实的树木模型，从而可更好地应用于林业资源调查、树木生长模拟等研究。由于人为因素或扫描仪自身的缺陷，使得获取的三维数据不可避免地带有噪声，而噪声会对后继相关的数字几何处理产生极大影响[2]。为了使点云数据能够更好地运用到后期的处理过程，满足曲面拟合及三维建模、网格化等对数据高质量的要求，必须先对原始数据进行去除噪声方面的预处理。

国内外许多研究学者在这方面做了深入的研究。Jones等[3]根据各顶点的邻域点来预测顶点位置，该方法的优点是不需要进行迭代计算。肖春霞等[4]采用协方差分析方法获取点云模型上数据点的平均曲率，提出了基于平均曲率流的点云模型去噪算法。Clarenz等[5]通过在点云模型上解一个离散的各向异性的几何扩散方程，实现各向异性的点云模型去噪。Buades等[6]提出2D图像的非局部均值去噪，使用其他与该像素点有相似邻域的像素来给该像素去噪。Wang等[7]基于几何密度和采样点特征的相似性，提出了点集曲面的非局部去噪算法。Jean-Emmanue等[8]基于局部曲面描述的相似性，提出了3D点云的非局部去噪算法，算法为每个采样点邻域内定义局部坐标系，计算两个点之间局部曲面描述相似性的权值，最后加权平均所有相似点，求得当前点的值。上述方法存在许多不足，例如方法计算量大、稳定性差、点云模型的原始特征难以保持等，并且去噪算法在树木点云数据处理中的研究应用甚少。

双边滤波由Tamasi等人提出，能同时利用邻域内像素点的空间邻近度信息和灰度邻近度信息，通过一系列的计算和删除操作实现降低噪声的目的，又可保持原始数据边缘细节的滤波技术。该方法首先用于滤除图像噪声，Durand等人[9]将双边滤波器用于数字图像处理上，后来逐步被应用到点云数据处理中。双边滤波方法是一种局部加权平均，其加权系数由两个因子决定[10]：一个是空间权系数因子σc（空间邻近度因子），一个是灰度权系数因子σs（灰度邻近度因子）。双边滤波用于去噪处理时，就是用周围点灰度值的加权平均来代替当前点的灰度值，权因子不仅与当前点和周围点之间的几何距离有关，而且与它们的灰度值差异有关。

1 双边滤波点云模型去噪方法

在三维点云数据的滤波中，定义

式（1）中：r为数据点，α为双边滤波权因子，n为数据点r的法向。当数据点的法向未知时，用最小二乘拟合平面的法向来估计数据点的法向[11]。

双边滤波的主要思想是计算权重因子，使得模型的数据点沿着法向方向移动，以此来光顺噪声，与图像双边滤波相类似，点云模型的双边滤波权因子α定义[12]如下：

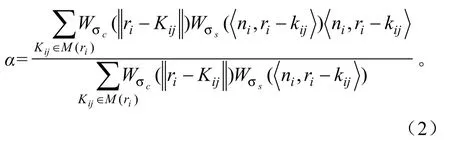
式（2）中：M(ri)={rij}1≤j≤k是数据点gi的邻近点，光顺滤波是标准高斯滤波，定义为：

特征保持权重函数类似于光顺滤波，定义为：

式（3）～（4）中：参数σc是数据点ri到每个邻域点的距离对该点的影响因子；参数σs是数据点ri到邻近点的距离向量在该点法向ni上的投影对数据点ri的影响因子。

下面是点云双边滤波去噪的算法步骤：

（1）读入点云数据，求出点云模型的数据量；

（2）对于每一个数据点ri，求出它m个近邻点，Kij，j=1，…，m；

（3）对于每一个邻近点，求出光顺滤波函数的参数值x（x=‖ri-Kij‖，为点ri到邻近点Kij的距离）；计算特征保持权重函数的参数值y（y=〈ni，ri-Kij〉，为点ri与邻近点的距离向量ri-Kij与该点的法向量的内积）；

（4）按照公式(3)和(4)计算出双边滤波函数值Wc(x)和Ws(y)；

（5）将Wc(x)和Ws(y)代入公式（2），计算出双边滤波权因子α；

（6）根据式（1）：ri:=r+αni，计算经过滤波后的新数据点；

（7）当所有的数据点都经过更新后，程序结束。

2 实验结果和分析对比

本文实验所用点云数据由法如公司FARO Laser120三维激光扫描仪测量获得（以.xyz文件存储），双边滤波去噪算法在主频2.80 GHz、内存6.0 GB的DELL T3500图形工作站上采用VC++编程语言环境实现。首先以一棵3年生紫叶矮樱为实验数据，树高1.80 m，南北最大冠幅0.94 m，东西最大冠幅0.76 m，扫描后数据点数为108 418。为更好地对去噪效果进行对比，截取树木，取主干树高方向0.55～0.85 m之间的数据进行放大。图1～图5中，(a)为树木整体效果图，(b)为主干0.55～0.85 m处的点云分布情况。其中，图1中(a)为去噪前树木整体效果图，(b)为主干处的点云分布图。图2、图3、图4、图5、图6分别为σc=10，并取σs=1、σs=10、σs=20、σs=50、σs=100 时，树木整体去噪效果图(a)和截取处点云分布图(b)，当σs依次取上述4个值时，去除的噪声点数分别为 3 891、15 497、24 861、54 273、69 731。模型点数变化如表1所示。

图1 去噪前效果Fig.1 Effect before de-noised

图2 去噪效果 (σc =10，令 σs =1)Fig.2 De-noising effect (σc =10, σs=1)

图3 去噪效果 (σc =10，令 σs =10)Fig.3 De-noising effect (σc =10, σs=10)

图4 去噪效果（σc =10，令 σs =20）Fig.4 De-noising effect (σc =10, σs=20)

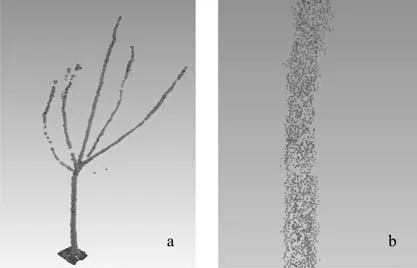
图5 去噪效果（σc =10，令 σs =50）Fig.5 De-noising effect (σc =10, σs=50)

图6 去噪效果（σc =10，令 σs =100）Fig.6 De-noising effect (σc =10, σs=100)

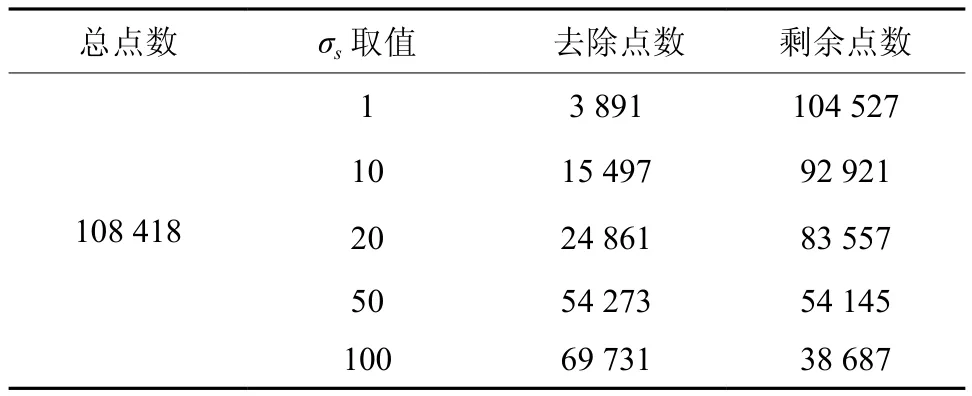
表1 不同σs取值下模型的点数变化情况和所用时间Table 1 Different values of point model and taken time under σs changes

当σs=10，σc依次取值1、20、50时，图7、图8、图9分别显示了树木的整体(a)和截取部分(b)的去噪效果，去除的噪声点数分别为3 845、3 998、4 899。模型点数变化如表2所示。

图7 去噪效果（σs =10，令 σc =1）Fig.7 De-noising effect (σs =10, σc =1)

图8 去噪效果（σs=10，令 σc =20）Fig.8 De-noising effect (σs =10, σc=20)

图9 去噪效果（σs=10，令 σc =50）Fig.9 De-noising effect (σs =10, σc=50)

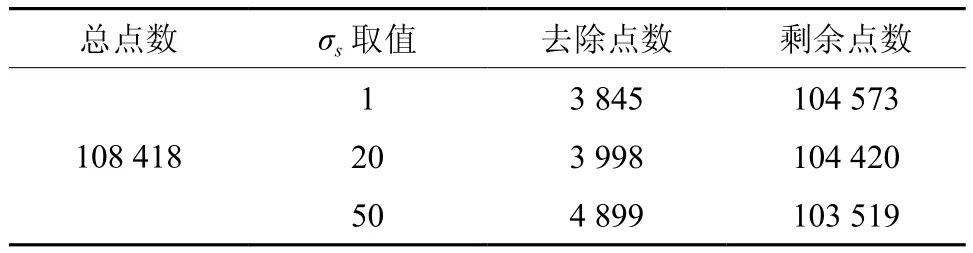
表2 不同σc取值下模型的点数变化情况Table 2 Different values of point model under σc changes

在Geomagic软件中选择减少噪声的功能，图10、图11分别显示选取迭代次数m=2，偏差限制值为n=0.005 mm和迭代次数为m=5，偏差限制值为n=0.001 mm的去噪结果，结果显示软件处理结果去噪效果较差，去除噪声点数也不能统计。若在Geomagic中，手动选取噪声点并删除，耗费时间过大，去噪效果同样较差。

图10 去噪效果（m=2，n= 0.005）Fig.10 De-noising effect (m=2, n= 0.005)

图11 去噪效果（m=5，n= 0.001）Fig.11 De-noising effect (m=5, n= 0.001)

实验结果表明，双边滤波器的两个参数σc和σs表示保持模型特征的大小和对比度，直接决定着点云模型整体的噪声去除效果。由图1～图9可以看出，当σc=10和σs= 20时的去噪效果较好，当σs=50和100时，去除的噪声点过多，大量有效点云数据被去除，模型边界被破坏。经过对比发现，双边滤波算法在噪声去除和树木扫描原型保护方面强于软件处理的效果。

3 应 用

以5年生桑树（树高3.98 m，南北最大冠幅1.20 m，东西最大冠幅1.15 m，原始数据点数380 495）和4年生毛白杨（高3.54 m，南北最大冠幅1.52 m，东西最大冠幅1.60 m，原始数据点数455 993）这2个扫描获取的点云模型为实验样例，在σc=10，σs= 20取值下，图12、图13显示了2个模型的去噪效果，其中(a)为去噪前效果图，(b)为去噪后效果图。2个模型去除的噪声点数分别为87 337和105 662，剩余数据点数分别为293 158和350 331，可以看出在合理的参数取值情况下，双边滤波算法的去噪效果明显，并且与原模型保持较高的相似性。

图12 桑树去噪效果（σc =10，令σs =20）Fig.12 Mulberry denoising effect (σc =10, σs=20)

图13 毛白杨去噪效果（σc =10 ，令σs =20）Fig.13 Populus tomentosa denoising effect (σc =10, σs=20)

4 结论与讨论

本文将双边滤波算法应用到树木点云去噪的研究中，实验初始时，双边滤波算法需要根据经验预先设置参数，但不能保证合理的参数取值。在对空间参数σc和灰度参数σs不断地调整变化中，得出以下结论：当两个参数的值接近于零时，双边滤波不会对输入图像产生任何作用；σs越大，滤波效果越明显，但特征保持能力就越弱（点云模型更多的纹理特征被平滑掉）；在σc取值较小的前提下，双边滤波器可以既实现有效地去噪又确保对点云模型轮廓的保护，并且σc的改变，对模型中去除的噪声点数数值的变化影响较少。

文中选取的σc=10，σs= 20参数较合理，使得双边滤波算法内存开销不大，计算复杂度较低，并且去噪后的点云边界细节跟树木本体差异较小，不会对边界数据产生很大的损坏。可见经双边滤波算法处理后的数据，足以满足后期点云数据建模以及参数提取等操作需求，同时，该方法在点云去噪处理中具有较好的实用性和研究意义。本研究中所选的参数并非最优参数，寻找最优仍需作进一步的研究，同时，缩减算法运行时间、优化算法自身稳定性以及易于硬件实现等方面的问题也是今后研究工作的重点。

[1] 张 帆,康宝生.点云数据几何处理方法研究[D].西安：西北大学,2013.

[2] 杜小燕,姜晓峰,郝传刚,等.点云模型的双边滤波去噪算法[J].计算机应用与软件,2010,27(7): 245-246.

[3] Jones T, Durand E, Desbrun M.Non-iterative Feature Preserving Mesh Smoothing[C].Proceedings of SIGGRAPH, 2003:943-949.

[4] Xiao C X, Miao Y W, Liu S,et al.A dynamic balanced flow for filtering point-sampled geometry[J].The Visual Computer, 2006,22(3): 210-219.

[5] Clarenz U, Rumpf M, Telea A.Fairing of point based surfaces[C]In Computer Graphics International, 2004: 600-603.

[6] Buades A, Morel J M.A non-local algorithm for image denoising[C].Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2005.

[7] Wang R F, Chen W Z, Zhang S Y,et al.Similarity-based denoising of point-sampled surfaces[J].Journal of Zhejiang University (Science A), 2008,9(6): 807-815.

[8] Deschaud J E, Goulette F.Point cloud non local denoising using local surface descriptor similarity [C].Paparoditis N, Pierrot D M, Mallet C.IAPRS, France, 2010.

[9] Yoshizawa S, Belyaev A, Seidel H P.Smoothing by example:Mesh denoising by averaging with similarity-based weights[C].Proceedings of the IEEE International Conference on Shape Modeling and Applications,2006.

[10] 张志强,王万玉.一种自适应的图像双边滤波方法[J].中国图像图形学报,2009,14(3):443-447.

[11] Tomasi C, Manduchi R.Bilateral Filtering for Gray and Color Image[C].Proceedings of the Sixth International Conference on Computer Vision, 1998: 839-846.

[12] 王丽辉,袁保宗.三维点云数据处理的技术研究[D].北京：北京交通大学,2011.

Method on tree point cloud model de-noising based on bilateral filtering

GUAN Xi-peng1, CHEN Yu-tuo1, ZHANG Huai-qing2, LIU Min2, LI Yong-liang2
(1.School of Computer Science and Technology, Central South University of Forestry and Technology, Changsha 410004, Hunan,China; 2.Research Institute of Forestry Resource Information Technology, Chinese Academy of Forestry, Beijing 100091, China)

For the problems of noises in trees point cloud data obtained by a three-dimensional laser scanner, by combining bilateral filtering algorithm, through two kinds of states in parameter values were set that the spatial proximity factor valueσcunchanged, while gray proximity factorσschange andσsvalue unchanged, whileσschange.According to the bilateral filtering weight factors, the adjacent sampling points were removed because it is too large with the current sampling point and update all data points.After filtering, the new data points were gotten.After comparatively analyzing the de-noising results of the two different parameter values state, the reasonable parameter values were obtained and thus realizing the purpose of the de-noising processing in trees point cloud model and maintaining the original features.Finally, two suitable experimental data models were selected, and the experimental results were validated further.The experimental results show that the algorithm is simple and efficient and noise removal works well.It has good practicability and significance.

measuring trees; bilateral filtering algorithm; point cloud de-noising; space proximity; gray proximity

S758

A

1673-923X(2015)09-0083-05

10.14067/j.cnki.1673-923x.2015.09.014

2014-09-18

国家863计划资助项目（2012AA102002）

管西鹏，硕士研究生 通讯作者：陈宇拓，教授；E-mail：cyt28@126.com

管西鹏,陈宇拓,张怀清,等.基于双边滤波算法的树木点云模型去噪方法研究[J].中南林业科技大学学报,2015,35(9):83-87.

[本文编校：谢荣秀]