杉木人工林树冠表面积及体积模型的研究

涂宏涛，孙玉军，吴明钦，王明初，杨星华

（北京林业大学 省部共建森林培育与保护教育部重点实验室，北京 100083）

杉木人工林树冠表面积及体积模型的研究

涂宏涛，孙玉军，吴明钦，王明初，杨星华

（北京林业大学 省部共建森林培育与保护教育部重点实验室，北京 100083）

以福建杉木Cunninghamia lanceolata人工林为研究对象，基于15块样地的33株标准木的解析数据，探讨了树冠平均表面积、最大表面积、平均体积、最大体积4个复合指标的预测模型。结果表明：4个树冠复合指标与胸径、树高、冠长、冠幅之间呈显著相关，相应的增加变量可提高模型的拟合精度，但当模型变量增加到2个以上时，模型精度提高不大。模型检验结果表明，以冠幅和冠长为变量的树冠表面积模型为最优；树冠体积以冠幅、冠长和树高为变量的模型为最优。模型的预估精度P均大于70.3%，说明模型可以较好地预估杉木人工林的树冠表面积和体积。

杉木人工林；树冠表面积；树冠体积；预测模型

树冠是树木的重要组成部分，是树木营养物质的重要提供场所，其大小能够体现树木间的竞争以及受环境影响的水平[1]。同时，树冠结构是树木生长及其与环境相互作用、反馈调节的综合结果，也是经营措施的具体表现[2-3]，树冠结构主要由枝条数、冠长、树冠表面积及体积等组成，它不仅影响各器官的空间分布，而且还影响林木截取光照进行光合作用的效率，因此研究树冠结构特征，对研究林木生长状况具有重要的意义[4]。

国内外对于树冠的研究相对较多，如Hamilton[5]研究表明树冠是树木材积增长最重要的因素；Sprinz、Smith等[6-9]认为树冠对于整个森林生态系统发育非常重要；Hasenauer等[10]采用非线性逻辑斯蒂模型（LM）建立奥地利主要树种树冠率模型来预测树冠的衰退及生长动态；周国模等[11]研究了雷竹林冠层特性与叶片的空间分布；梁军等[12]通过分析生长指标与树冠特性间的相关关系，得出冠层疏密度对于林木生物量和材积生长量呈负相关关系。但对于杉木人工林树冠表面积和体积的定量模型研究较少[13-14]，由于树冠结构复杂，很难对其进行准确的测算，如果具体测量树冠表面积和体积需要耗费大量的人力、物力和财力[15]。目前，树冠表面积和体积的计算方法主要有几何体法、平均断面积求积法、树冠轮廓模型法、激光扫描法4种[16-19]。

本研究以福建将乐林场杉木人工林为研究对象，采用几何体法和平均断面积法求算树冠的表面积和体积，并构建树冠表面积和体积等指标与林木胸径、冠幅等易测林木变量的预估模型，为准确估算树冠表面积和体积提供科学合理的方法，从而为进一步研究林木生长和林分结构提供参考依据。

1 试验地概况

试验区位于福建省将乐县国有林场（117°05′～ 117°40′E，26°25′～ 27°04′N），地势呈西北、东南高，中间低，大致呈西南向东北延伸的山间盆谷，平均海拔在400～800 m。气候属中亚热带季风气候，四季分明，干湿明显，年平均气温14.6～18.7 ℃，年平均降水量1 676.3 mm，年平均蒸发量1 204 mm。土壤以红壤为主，并分布有黄红壤，土层深厚，土质较好的一般为沙壤土或轻壤土，水分充足，土壤肥沃。植被以亚热带植物区系为主，植被种类非常丰富，主要的乔木有：杉木Cunninghamia lanceolata、马尾松Pinus massoniana、湿地松Pinus elliottii等；林下植被主要有黄瑞木Cornus alba、粗叶榕Ficus hirta、盐肤木Rhus chinensis、五节芒Miscanthus floridulus、芒萁Dicranopteris dichotoma、乌蕨Stenolomachusanum等。

2 材料与方法

2.1 数据的收集与整理

本研究于2010至2012年在福建将乐国有林场杉木人工林，根据林分不同年龄、密度，以典型抽样原则设置了15块20 m×30 m标准地。对标准地内的林木进行每木检尺，在每块标准地选取2～3株标准木共33株，伐倒并进行解析木的测定。分别测定解析木的胸径（D）、树高（H）、冠幅（C）、活枝下高（HCB）、冠长（CL）和每个枝条的着枝深度（BH）、着枝角（BA）以及枝长（BL）等因子。从33株样木中选取10株作为模型拟合的检验数据。解析木的具体做法参见文献[20-21]。

对于树冠表面积和体积，结合几何体法和平均断面积法，将树冠按1 m分成若干层，将树冠顶层视为圆锥体，树冠底层为倒圆锥体，中间部分为圆台。以每层的平均枝长和最大枝长与着枝角的三角函数关系求出各个区分冠层顶部和底部的半径（CR）。

根据圆锥体、圆台表面积和体积的计算公式（式2～式5）求算树冠各冠层的表面积和体积，剔除树冠底层不连续的冠层，累加各冠层表面积和体积得到全树冠平均表面积（CSA1）、最大表面积（CSA2）、平均体积（CV1）和最大体积（CV2）。各标准木主要测树因子数据如表1所示。

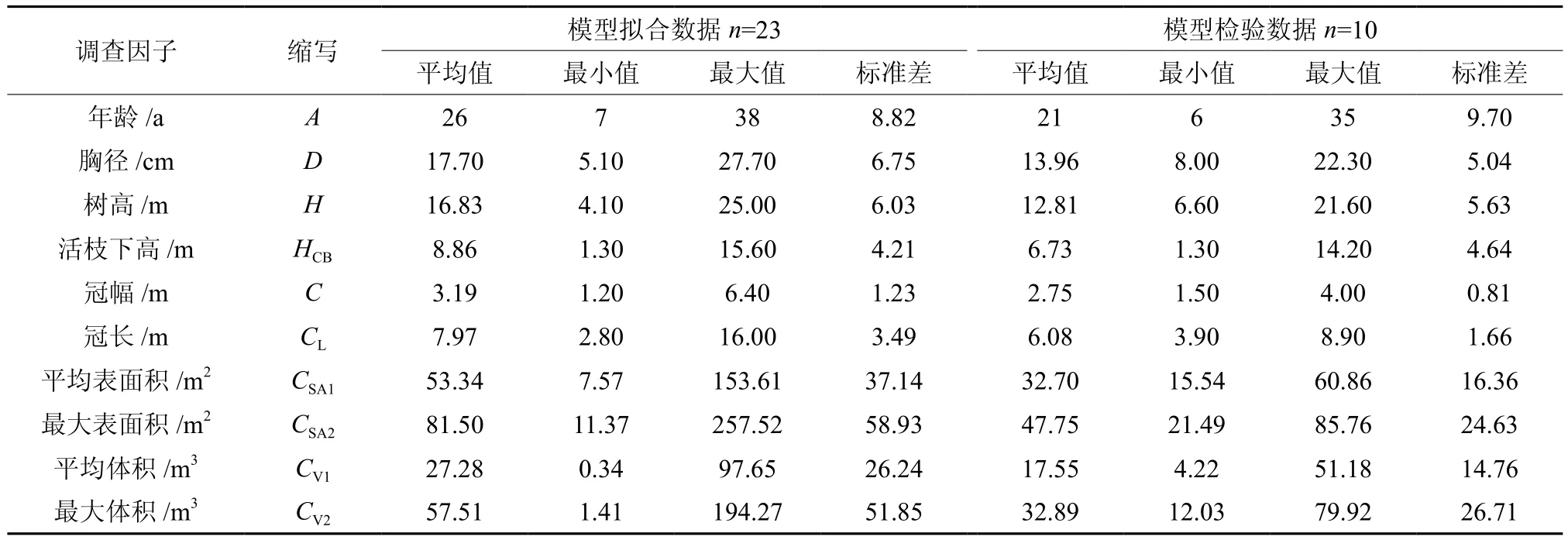
表1 杉木标准木主要测树因子数据统计Table 1 Statistical data of main measuring tree factors of Chinese fir model trees

式中：h为每个冠层的长度；R为冠层底部的半径；r为冠层顶部的半径。

2.2 树冠模型的构建

2.2.1 树冠模型结构的设计

研究表明异速生长方程（式6）能够很好地拟合树冠的表面积和体积模型[22]。本文根据33株解析木数据，选取23株样木的数据来建模，剩余10株为模型检验数据。运用R软件进行回归分析，构建树冠模型。模型方程如下：

式中：y为树冠表面积或体积；x1、x2、xi为林木变量；a、b、c、n为模型参数。

2.2.2 模型变量的筛选

根据实测数据所得33株样木的胸径、树高、冠长、冠幅等林木变量与树冠平均表面积、最大表面积、平均体积和最大体积进行Pearson相关分析，可知除活枝下高外，各林木变量均与树冠表面积和体积显著相关（见表2）。因此，以其4个林木变量作为模型拟合的变量。

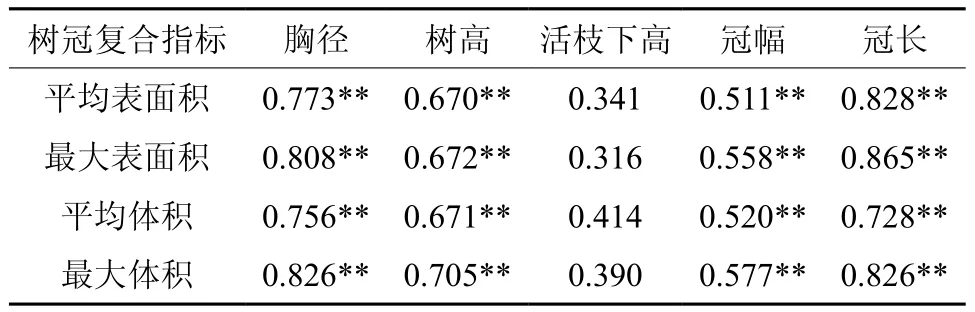
表2 林木变量与树冠表面积、体积的Pearson相关分析†Table 2 Pearson relation analysis between tree variables and crown surface area and volume

2.2.3 模型评价与检验

对建模样本进行检验，计算检验指标，评价模型优度。用于模型评价与检验的指标主要有R2（拟合优度或判断系数）、P（预估精度）、S（剩余标准差）、平均相对误差（E）、平均相对误差绝对值(e)[23]。R2、P越接近1越好；S、E、e越接近0越好。

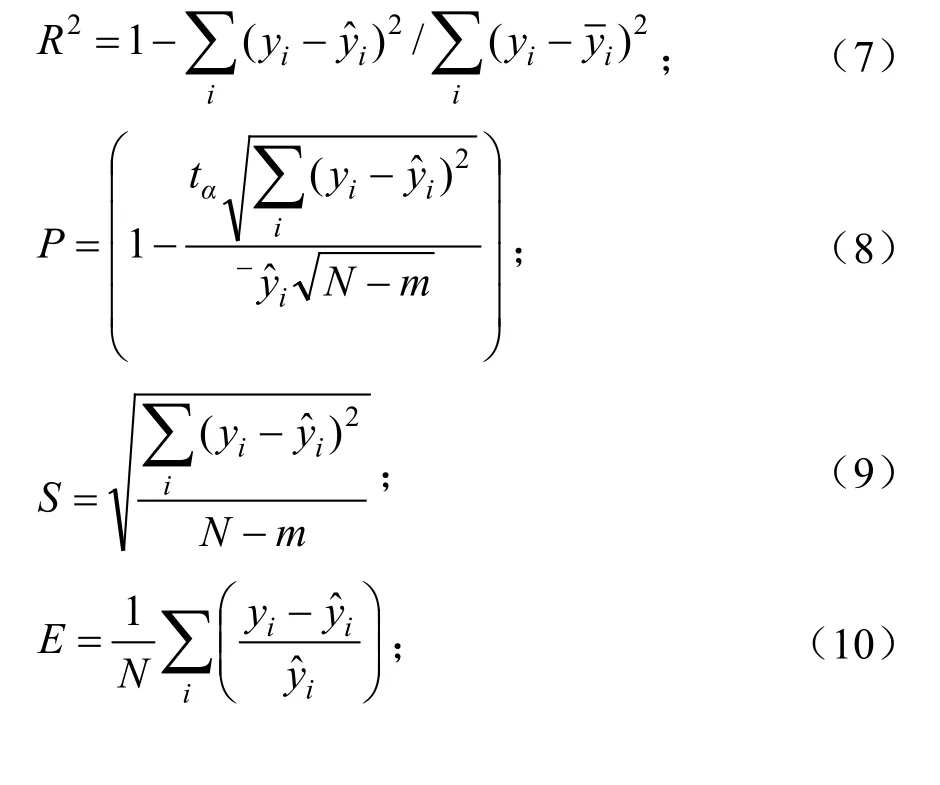
式中，yi为实测值；iyˆ为估计值；为实测平均值；为预估平均值；N为样本数；m为模型中参数的个数；tα为置信水平为α时的t分布值（α=0.05，tα=1.98）。

3 结果与分析

3.1 树冠表面积和体积模型

以林木变量拟合树冠表面积和体积预估模型，开始只引入单变量为拟合模型变量，不断增加拟合变量至四元变量模型，分别选取各元拟合模型中R2、P最大的模型，结果见表3。求解参数估计值、评价指标值和各元方程的F检验值。

由表3可以看出，随着模型变量的不断增加，模型方程的R2（拟合优度或判断系数）不断增大，P也整体呈增加趋势，模型的精度不断提高；但当模型变量数超过两个后，R2和P增加不明显。在树冠模型中，一变量模型的拟合优度最低，R2＜0.70，P＜80.00%；四变量的最大，R2＞0.74，P＞80.5%；从整体来看，树冠平均体积模型的拟合优度最小，树冠最大表面积模型的拟合优度最大。所建立的预估模型，树冠平均表面积中，以三变量模型方程3的判断系数R2和预估精度P最大；树冠最大表面积中，以四变量模型方程4的判断系数R2和P最大；树冠平均体积中，以四变量模型方程4判断系数R2最大，以三变量模型方程3预估精度P最大；树冠最大体积中，以四变量模型方程4判断系数R2和预估精度P最大。

通过F检验得出树冠表面积和体积的最优变量模型，即如果两个方程F检验值显著，则选取R2、P较大的模型方程；如果两个方程F检验值不显著，则选取变量数较少的模型方程，对于树冠平均表面积和最大表面积，以C、CL双变量模型方程2为最优（R2=0.78、R2=0.80；P=86.00%、P=86.10%）；对于树冠平均体积和最大体积，以C、CL、H三变量模型方程3最优（R2=0.74、R2=0.78；P=80.50%、P=81.30%）。综上所述，树冠表面积的大小主要受冠幅、冠长的影响，选取模型方程2来估算树冠的平均表面积和最大表面积；树冠体积大小主要受冠幅、冠长和树高的影响，选用模型方程3来估算树冠平均体积和最大体积。

表3 杉木树冠表面积和体积模型拟合结果†Table 3 Fitting results of crown surface area model and crown volume model for C.lanceolata

3.2 树冠最优模型的检验

通过未参与建模的10株样木数据，根据表3的F检验所得出的树冠表面积和体积最优模型进行检验，检验结果如表4所示。树冠平均表面积和最大体积的预估精度P都达82.99%以上，平均相对误差E分别为-0.12、-0.14；树冠平均体积和最大体积的预估精度P达70.30%以上，平均相对误差E为0.35、0.23。总体而言，树冠模型方程的拟合优度R2均达0.80以上，因此，模型能很好地预估树冠表面积和体积。

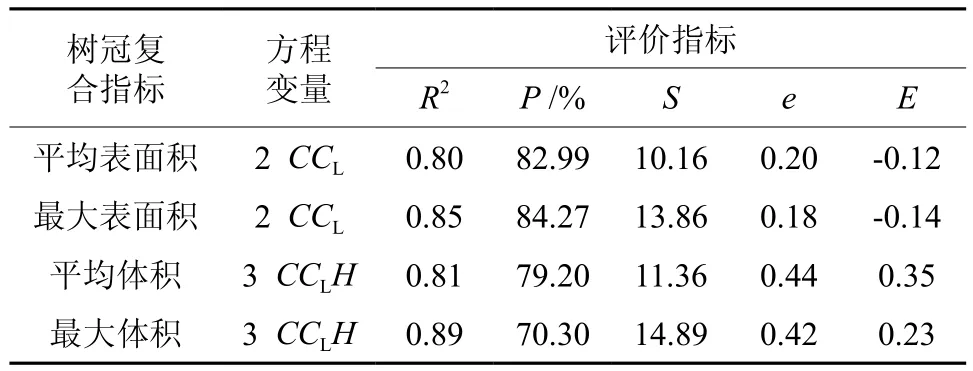
表4 杉木树冠模型检验结果Table 4 Test results of crown model for C.lanceolata

以树冠表面积和体积最优模型预估出所有样木树冠平均表面积、最大表面积、平均体积和最大体积的理论值，分析理论值与实际值的相关关系（见图1）。树冠最大表面积、最大体积的理论值与实际值较相近，其模型拟合效果较优；而树冠平均表面积、体积的理论值与实际值关系点较为分散，其原因可能是在树冠模型拟合中，主要是以林木最长树枝作为模型变量冠幅，因此，以其为变量拟合的树冠表面积和体积最大值的理论值与实际值相关性较为接近；而树冠平均表面积和体积的理论值和实际值相关性较差。

4 结 论

本研究以福建杉木人工林中33株杉木为研究对象，采用分层切割法计算树冠整体表面积和体积，同时以异速生长方程来拟合树冠表面积和体积模型。得出以下结论：

（1）杉木树冠表面积和体积随着林木变量的增大而增大，与胸径、树高、冠长、冠幅显著相关，其中与冠长的相关系数最高；异速生长方程能很好地拟合杉木树冠表面积和体积模型。林木变量数的增加能适当地提高模型拟合的精度，但当林木变量数超过2个后，模型精度提高不大。

（2）树冠表面积模型中，以冠幅、冠长为变量的双变量模型来拟合杉木树冠平均表面积和最大表面积最优，模型的判断系数R2达0.80以上，模型的预估精度P达82.99%以上，所建立的模型具有较高的估测精度，平均树冠表面积模型为，最大树冠表面积模型为；树冠体积模型中，以冠幅、冠长、树高为变量的三变量模型来拟合杉木树冠平均体积和最大体积最优，模型的判断系数R2达0.81以上，模型的预估精度P达70.30%，树冠平均体积模型为，树冠最大体积模型为

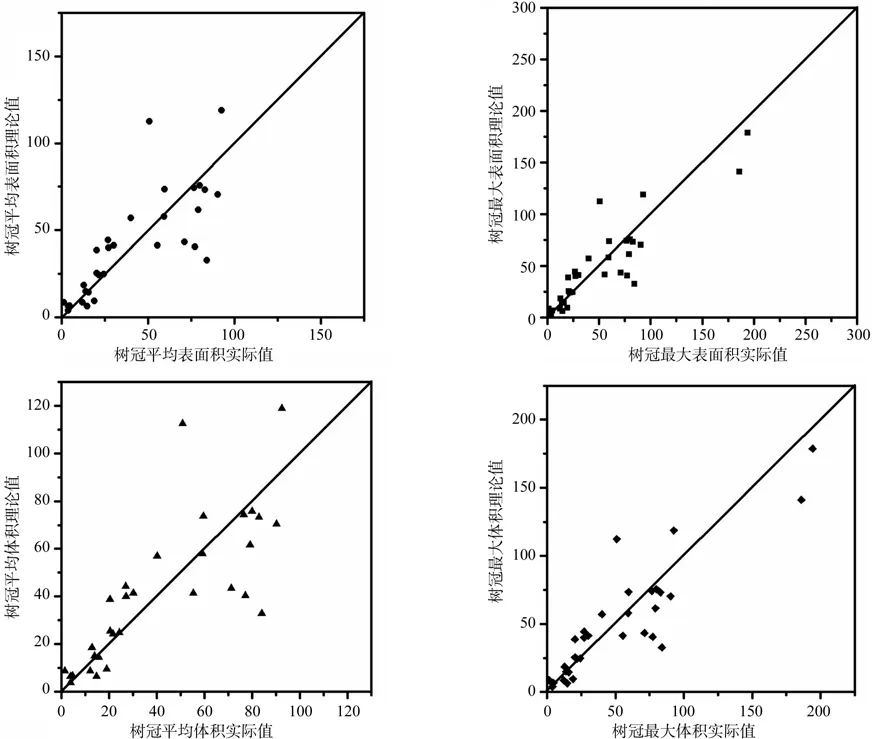
图1 树冠表面积和体积的实测值与理论值的相关关系Fig.1 Relationship between measured values and theoretical values of crown surface area and crown volume

（3）由于林木冠幅和冠长在野外测定中比较困难，且人为误差较大，因而在满足一定的估测精度条件下，以胸径建立的单变量模型预测树冠表面积和体积的预估精度也达70.9%以上，因此，可以直接利用胸径单变量来预估树冠的表面积和体积。本文中所建立的林木树冠表面积和体积模型可以预估杉木人工林林木的树冠表面积和体积，其应用于林分结构的分析和优化还需要进一步的研究。

[1] 姜石磊.黑龙江省主要针叶树种树冠形状模型的研究[D].哈尔滨：东北林业大学, 2012.

[2] 朱春全.集约与粗放经营杨树人工林树冠结构的研究[J].林业科学, 2000, 26(2): 60-68.

[3] 刘艳艳.樟子松人工林树冠结构的研究[D].哈尔滨:东北林业大学, 2005.

[4] 周国模, 金爱武.雷竹林冠层特性与叶片的空间分布[J].林业科学, 1999, 35(5): 17-21.

[5] Hamilton G J.The dependence of volume increment of individual trees on dominance, crown dimensions, and competition [J].Forestry, 1969, 12(1): 133-134.

[6] Sprinz P T, Burkhart H E.Relationships between tree crown,stem, and stand characteristics in unthinned loblolly pine plantations [J].Can.J.For.Res., 1987, 17(6): 534-538.

[7] Kramer H.Crown development in conifer stands in Scotland as influenced by initial spacing and subsequent thinning treatment [J].Forestry, 1996, 39(1): 40-59.

[8] Smith W R, Farrar R M, Murphy P A Jr,et al.Crown and basal area relationships of open-grown sourthern pines for modeling competition and growth [J].Can.J.For.Res.,1992,22(3):341-347.

[9] Ford E D.Branching, crown structure, and the control of timber production[C] //Connell M G R, Jackson J E I.Attributes of trees as crop plants.Huntingdon: Institute of Terrestrial Ecology,1985:228-245.

[10] Hasenauer H, Monserud R A.A crown ratio model for Austrian forests [J].Forest Ecology and Management, 1996, 84(1): 49-60.

[11] 贾炜玮.樟子松人工林枝条生长及节子大小预测模型的研究[D].哈尔滨: 东北林业大学,2005.

[12] 梁 军, 徐锡增, 吕士行, 等.I-69杨生长过程分析和生长阶段划分[J].林业科学研究, 2000, 13(4)：343-348.

[13] 杜 娟, 范志霞, 叶顶英,等.楠木人工林树冠体积与叶面积指数预估模型的研究[J].浙江林业科技,2010,30(4)：37-41.

[14] 廖彩霞, 李凤日.樟子松人工林树冠表面积及体积预估模型的研究[J].植物研究,2008,28(5)：632-636.

[15] 刘 平, 马履一, 等.油松、侧柏树冠复合指标模型的建立及其对林分健康性的评价[J].东北林业大学,2009,37(3):32-35.

[16] 刘兆刚, 刘继明, 李凤日, 等.樟子松人工林树冠结构的分形分析[J].植物研究,2005,25(4):465-470.

[17] 郑治刚, 李怀玉, 廖雅萍, 等.树冠空间体积的计算方法[J].林业资源管理, 1986, 2(1):35-40.

[18] 巩垠熙, 何 诚, 冯仲科, 等.基于改进Delaunay算法的树冠三维重构单木因子提取[J].农业机械学报, 2013,44(2):192-199.

[19] 熊妮娜, 王 佳, 罗 旭, 等.一种基于三维激光扫描系统测量树冠体积方法的研究——以油松为例[J].北京林业大学学报, 2007, 29(增刊2): 61-65.

[20] 吴明钦, 孙玉军, 郭孝玉, 等.长白落叶松树冠体积和表面积模型[J].东北林业大学学报, 2014, 42(5): 1-5.

[21] 肖 锐, 李凤日, 刘兆刚,等.樟子松人工林分枝结构的分析[J].植物研究, 2006, 26(4): 490-496.

[22] 卢 军, 李凤日, 张会儒, 等.帽儿山天然次生林主要树种冠长率模型[J].林业科学, 2011, 7(6): 70-76.

[23] 李际平, 郭文清, 曹小玉,等.基于非线性度量误差的马尾松相容性立木生物量模型[J].中南林业科技大学学报, 2013,33(6): 22-25.

Predicting models of crown surface area and crown volume forCunninghamia lanceolataplantation

TU Hong-tao, SUN Yu-jun, WU Ming-qin, WANG Ming-chu, YANG Xing-hua
(Key Lab.for Silviculture and Conservation Co-constructed by China Ministry Education and Beijing, Beijing Forestry University,Beijing 100083, China)

Based on the data of 33 sample trees from 15 permanent plots inCunninghamia lanceolataplantations, the predicting models of crown average-surface area, crown max-surface area, crown average-volume, crown max-volume were discussed and were studied and set up.The results show that these four crown composite indexes had significant relationships with other four tree variables, such as diameter at breast height, tree height, crown length, and crown width, the number increasing of tree variables can improve the fitting precision of the models, when the number increasing of tree variables were over two, the fitting precision of models cannot be obviously improved.The model test results show that the tree crown surface area model with crown length and tree height as the variables was the optimal; the crown volume model with crown width, crown length and tree height as the variables was the best; The estimated precisions of the optimal models were greater than 70.3%.Therefore, the models developed in this study are suitable for estimating the crown surface area and crown volume ofC.lanceolataplantations.

Cunninghamia lanceolataplantation; tree crown surface area; tree crown volume; forecasting model

S758.1

A

1673-923X(2015)09-0088-05

10.14067/j.cnki.1673-923x.2015.09.015

2014-01-15

林业科技成果国家级推广项目（[2014]26）；国家林业局重点项目（201207）

涂宏涛，硕士研究生 通讯作者：孙玉军，教授；E-mail：sunyj@bjfu.edu.cn

涂宏涛 ,孙玉军 , 吴明钦,等.杉木人工林树冠表面积及体积模型[J].中南林业科技大学学报，2015, 35(9): 88-92, 103.

[本文编校：谢荣秀]