舰船燃气轮机气路测量参数的理论选择方法
姜荣俊,高建华,刘永葆
舰船燃气轮机气路测量参数的理论选择方法
姜荣俊,高建华,刘永葆
(海军工程大学动力工程学院,武汉430033)
针对舰船燃气轮机气路性能监测诊断的有效性要求,归纳总结了气路测量参数选择要求,提出了1套系统完整的燃气轮机气路测量参数的理论选择方法。在可测量和易测量要求及测试精度要求的初步选择基础上,依次采用影响系数、相关系数和条件数对气路测量参数的敏感性、相关性和诊断误差等进行了分析,最终从理论上选择了某舰船3轴燃气轮机气路性能监测诊断的测量参数。实例表明该理论方法具有一定的通用性和工程应用价值,对燃气轮机气路测量参数的选择有一定的指导作用。
气路;测量;监测;诊断;舰船;燃气轮机
0 引言
发动机监测诊断是保证发动机安全运行、减少寿命费用、防止恶性事故的有效手段。进行燃气轮机监测诊断必须根据实际目标要求首先对其测量参数进行优化选择[1]。针对燃气轮机的气路性能监测诊断,Urban早在20世纪70年代就提出了气路分析(gas path analysis-GPA)技术[2],其原理是基于燃气轮机各部件间的气动热力学关系式建立小偏差故障模型,构建燃气轮机性能变化量与测量参数变化量的函数关系,从而实现利用带有噪声或偏置的气路参数对燃气轮机气路性能进行监测诊断。
为了较好地对燃气轮机的气路性能实施监测和诊断,基于各种要求和考虑,国内外学者对燃气轮机气路测量参数的选择进行了研究。Urban基于线性气路分析技术(LGPA—linear gas path analysis),提出采用诊断误差作为筛选测量参数的1个重要准则,并明确提出测量参数的数目不能少于性能参数数目[3];Consumi M和Agostino L d基于数据统计推理,根据不同的气路测量参数组合的诊断精度对测量参数进行了选择[4];Ogaji SOT等基于敏感度和诊断误差,分别利用线性和非线性气路分析方法(NLGPA—non-linear gas path analysis),对燃气轮机测量参数的选择问题做了进一步研究,结果表明在模拟单一气路故障情况下,根据NLGPA方法选择出的测量参数方案更为合理;而在多种气路故障情况下,NLGPA方法的优越性并不十分明显[5];唐耿林基于敏感性、相关性和诊断误差对航空发动机的性能测量参数进行了选择[6];孙祥逢等针对气路故障诊断主因子模型,基于敏感性、相关性和诊断误差对测量参数进行了选择,证明测量参数太多对采用故障方程的诊断不利,并尝试给出了解释[7]。
本文主要针对监测诊断结果的有效性,从理论上对某舰船3轴燃气轮机的气路监测诊断参数进行了优化选择,对于工程中的安全性、可靠性等因素则不予太多考虑。
1 气路测量参数的初步选择
某舰船3轴燃气轮机为带双转子燃气发生器的简单开式循环燃气轮机,其具体结构如图1所示,图中标识出其气路通道的各特征截面。考虑到稳态过程的气路容积效基本可以忽略,因此对于同一特征截面处的上1个部件出口和下1个部件的进口,可以认为其气路参数相同。

图1 3轴燃气轮机结构
燃气轮机的工作状态可用一定的特征量来描述,由这些特征量可以确定燃气轮机的完好性、工作能力和其动作的正确性。在燃气轮机气路监测诊断中,特征量通常指需要分析的部件特性参数或几何参数,如压气机效率、涡轮导向器面积等。在实际运行的不解体情况下,特征量通常是不可测量的。从特征量可以引出描述故障状态的故障因子[8]。而测量参数主要指可观测的且能区分发动机技术状态的状态量,这些参数主要是指气路各截面上能直接测量的参数(图1),如转子转速、温度、压力等[9]。燃气轮机的气路性能监测诊断主要是通过对其气路通道中压力、温度和转速等状态量的监测,实现对压气机、涡轮和燃烧室等部件的效率、流量等特性参数或几何参数特征量的诊断。
考虑到舰船燃气轮机中动力涡轮的气路性能故障通常较少,且其气路参数受负载(如螺旋桨)的影响较大,变化较复杂,因此一般不作为气路性能监测参数,但为了防止超速,仍需对其转速进行监控。由于燃烧室掉块、烧裂等故障不会引起发动机性能参数的明显变化[10],因此只分析与燃油喷嘴堵塞故障有关的燃烧室效率特征量。选取9个需要监测诊断的特征量:高、低压压气机的效率η和流量W;高、低压涡轮及动力涡轮的效率和流量;燃烧室效率。
舰船3轴燃气轮机,在一定的环境参数(大气压力、温度和湿度)和油门位置下,可以被用作气路监测诊断的参数主要有以下几种:(1)转速:包括高、低压压气机转速;(2)压力:包括高、低压压气机,燃烧室,高、低压涡轮的出口压力等;(3)温度:包括高、低压压气机,燃烧室,高、低压涡轮的出口温度等;(4)其它:包括燃油流量、发动机扭矩或功率等。
首先从可测量和易测量要求出发来分析以上气路测量参数:由于高速、高温、高压和气流影响,燃烧室出口、高压涡轮出口等处温度和压力往往比较难测出且成本较高,即使在台架试车非全流程参数测试情况下[11],这些参数也往往不测量,通常不作为气路监测诊断参数。为了检验不测量此处参数对气路监测诊断效果的影响,这里暂时考虑测量燃烧室出口、高压涡轮出口处温度和压力。
对这些参数的测试精度进行分析,相对台架试验条件,实际使用中通常会降低测试精度[11],但随着发动机测控技术的进步和测试标准的提高,在排除人为误差的情况下,认为其测试精度满足测量误差小于故障变化引起的测量参数偏差的要求。
基于以上步骤,除环境温度和压力、运行工况参数(油门位置等)的运行环境参数外,初步确定了13个气路测量参数:低压压气机的出口温度T1.5、出口压力P1.5、转速n1,高压压气机的出口温度T2、出口压力P2、转速 n2,燃烧室的出口温度 T3、出口压力 P3,高压涡轮的出口温度T3.5、出口压力P3.5,低压涡轮的出口温度T4、出口压力P4,发动机功率N。这13个参数是否能够满足敏感性、相关性和诊断误差等测量参数要求,还需进一步分析。在继续分析之前,首先对所采用的GPA方法进行介绍。
2 气路分析法介绍
GPA的原理是映射燃气轮机测量参数和特征量间的气动热力学关系[2,13],其一般形式的数学模型为

式中:输入矢量P∈Rp,为运行环境参数;P∈Rn,为特征量参数;输出矢量Y∈Rm,为气路性能测量参数。
某基准运行工况(用下标“0”表示),式(1)利用泰勒级数展开

式中:HOTs为偏差的高阶项,在小偏差的情况下忽略其影响,成为线性化方程。若运行环境参数与基准环境参数相同,则(P-P0)=0。式(2)简化为

以小偏差量来表示

A∈Rm×n,是影响系数矩阵(ICM-influence coefficient matrix),是 F(X,P) 关于特征量 X 的Jacobian矩阵

式(4)即经典的GPA小偏差方程,它反映了测量参数和特征量参数的关系。若矩阵A可逆,则得

式中:A-1为故障系数矩阵(FCM-fault coefficient matrix)。基于该线性化的关系式,通过测量参数变化量可得到燃气轮机部件特征量参数的变化量,从而实现对燃气轮机气路性能的监测诊断。
实践中往往很难得到实际发动机模型F(X,P)的精确解析形式,因此现在通常采用精确仿真模型的数值线性化的方法来得到影响系数矩阵A。且A通常为非正定矩阵,因此实际中很少直接采用式(6)来求解式(4),更多采用最小二乘等方法。
如果考虑测量误差因素ν,则式(4)为

以上是Urban早在1960年提出的基于小偏差方程的LGPA[14]。
3 气路测量参数的敏感性选择
对特征量敏感的测量参数才能暴露故障,因此可根据敏感性原则直接选择测量参数。表征系统的特征量的各状态量,都可以作为对系统进行技术监测诊断的主要依据。每个状态量对系统的故障部位和故障程度的敏感性不同,可以从这些参数中挑选出对故障特征量最敏感的状态量,也可以用某几个状态量组合成1个敏感性较大的综合参数。气路性能测量参数可通过测量与特定气路故障有关的状态量来直觉猜测,但基于GPA的方法往往更可取。根据GPA,利用小偏差原理,可以计算出特征量偏差和测量参数偏差之间的影响系数矩阵A。基于燃气轮机仿真模型,通过数值计算,可以得到某型舰船燃气轮机在1.0设计工况下的影响系数矩阵,具体数值见表1,该系数矩阵反应了测量参数对特征量的敏感性。测量参数对不同特征量变化的2种敏感性如图2所示。在描述敏感程度时,依据影响系数的绝对值大小,可分为:较敏感(≥0.50)和非常敏感(≥1.00)。
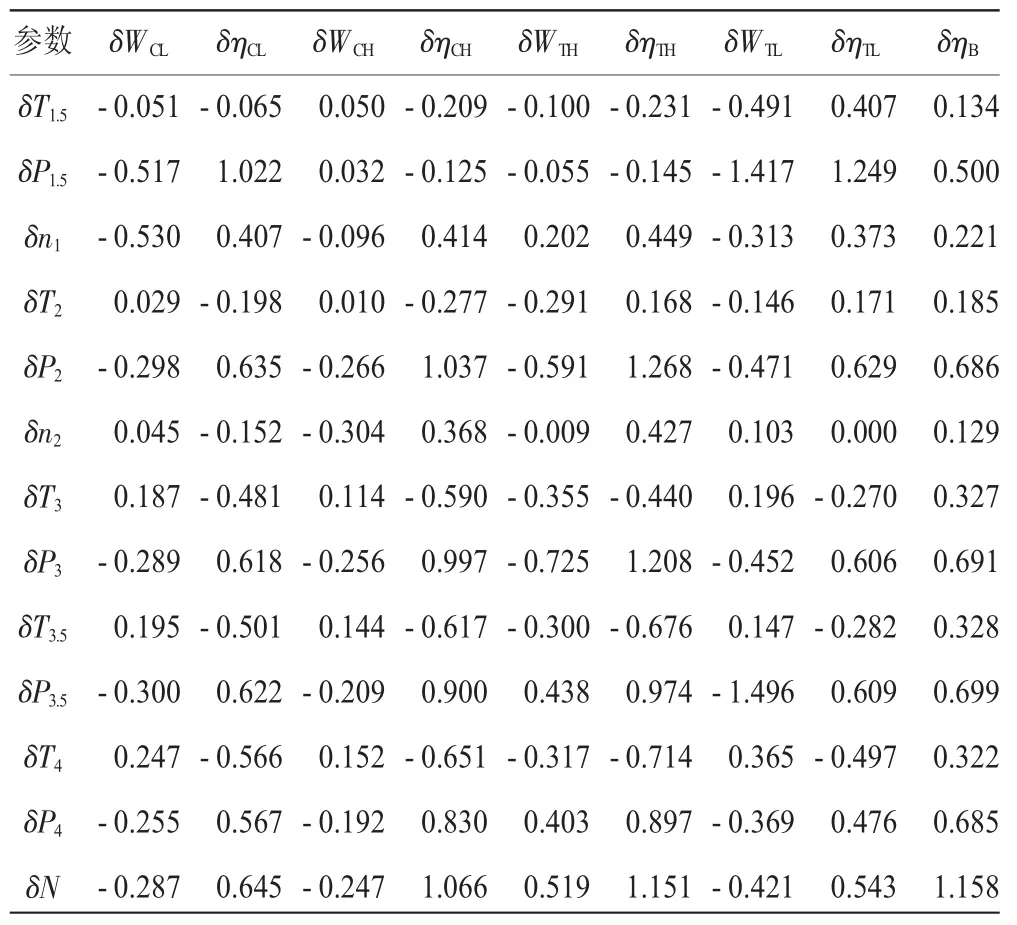
表1 某型舰船燃气轮机1.0设计工况下的影响系数矩阵

图2 不同特征量变化下测量参数的敏感性
(1)低压压气机对 δWCL,n1、P1.5较敏感;对 δηCL,P1.5、P2、P3.5、P3、N、P4、T4、T3.5较敏感。T1.5对包括低压压气机在内的性能特征量变化都不敏感,但对低压涡轮的特征量变化有比较突出的表现(绝对值仍较小),因此从低压涡轮气路性能的监测诊断需要出发,是否测量T1.5值得进一步分析。
(2)在高压压气机中,对于δWCH,几乎所有的参数都不很敏感。压气机叶片结垢、叶顶间隙增大会导致流量特征量变化,考虑故障监测诊断的需要,暂时保留相对较敏感的几个参数:n2、P2、P3、N(按敏感度从大到小排序,取影响系数绝对值≥0.25);对于δηCH,N、P2、P3、P3.5、P4、T4、T3.5、T3都较敏感。T2对包括高压压气机自身在内的特征量变化也不敏感,所以不测量该参数。
(3)在高压涡轮中,对于 δWTH,P3、P2、N 较敏感;对于 δηTH,P2、P3、N、P3.5、P4、T4、T3.5都较敏感。结合前述初步选择时对高温截面处测量参数的选择,确定采用温度相对较低且对高压涡轮特征量变化也非常敏感的 N、P2、P4、T4,而不测量 T3.5和 P3.5。
(4)在低压涡轮中,对于 δWTL,P3.5、P1.5、T1.5较敏感;对于 δηTL,P1.5、P2、P3.5、P3、N、T4都较敏感。结合前述分析,选择不测量 P3、P3.5。
(5)在燃烧室中,对于 δηB,N 非常敏感,P3.5、P3、P2、P4、P1.5也较敏感,根据前述分析,选择舍弃 P3.5、P3。通过敏感性分析,选择了 7 个测量参数:P1.5、n1、P2、n2、T4、P4、N。
4 气路测量参数的相关性选择
相关是指变量之间的线性关系。参数的相关性是指在不同故障作用下测量参数组变化之间的线性关系。对测量参数的相关性要求是:对不同的故障特征量,测量参数有不同的变化特征。即测量参数之间的相关性要尽量小,使所选择的测量参数不仅能够表现各部件特征量的变化,且对于不同的故障,测量参数能表现出不同的变化特征,达到隔离故障的目的[7]。相关性的强弱常用相关系数γxy表示,其值越接近于0,表示相关性越弱。另文献[6]提出:若某2个不同故障对同1组测量参数的影响相当,则该组参数对这2个故障是相关的,而某2个故障对同1组测量参数的影响方向相反,则不相关。因此相关性分析可以通过ICM中的正负符号进行判断。
综合这2种测量参数相关性判断方法,本文提出:
(1)若γxy接近0,则测量参数相关性小;
(2)若 γxy<0(负相关),则测量参数不相关;
(3)若γxy接近1,且能找到变化相反并足够敏感的测量参数,也认为测量参数不相关。
根据上面提出的3种判断方法,可以对气路测量参数进行相关性选择。
基于式(8),不同特征量下7个测量参数变化间的相关系数值见表2。


表2 不同特征量下测量参数变化间的相关系数值
从表2中可见:
(1)δWCL与 δWTL、δηCL与 δηTL、δηCH与 δηTH这 3 组特征量对应的测量参数变化间的的正相关性较强,因此基于现有的测量参数较难区分。
(2)观察 δWCL与 δWTL组合,P1.5对 δWTL变化非常敏感,其影响系数值是P1.5对δWCL的影响系数值的2.744倍,有可能据此来区分这2个特征量。另外依据判断方法(3)分析,从表1中可以发现T2的变化方向相反,但注意到它对δWCL和δWTL的变化都不敏感,影响系数分别为+0.029和-0.146,因此只有在保证足够测量精度的情况下才有可能区分这2个特征量的变化,所以是否选择T2值得考虑。
(3)观察 δηCL与 δηTL组合,从表 1 可以发现 T1.5变化方向相反,且对δηTL足够敏感,影响系数为+0.407,因此选择T1.5。
(4)观察 δηCH与 δηTH组合,从表 1 可以发现 T2的变化方向相反,且二者的影响系数值也足够敏感,综合考虑(2),因此确定选择T2。
通过以上相关性分析,在原来7个测量参数基础上增加了2个测量参数T1.5和T2。根据计算,测量参数增加后,以上3组特征量对应的测量参数变化间的正相关性都有所减弱,气路性能监测诊断的有效性有所提高。
5 气路测量参数的最终选择
通过以上步骤得到比较满意的测量参数组合。测量参数数目达到了气路监测诊断的最低要求,但监测诊断的效果还有待继续分析。
气路诊断的过程实际就是基于小偏差方程(4),根据已知的测量参数偏差求解未知性能特征量偏差的数值计算问题。用数值方法求解线性方程组(4),计算结果存在误差,原因主要有2个:一是选用的计算方法,为了保证算法的稳定性,采用选主元的高斯消去法,选主元的三角分解法等;二是方程组本身。一般来说,由于存在各种误差,线性方程组(4)的系数矩阵A与测量项δY的数值并不绝对正确[15]。对于这种偏离正确值的扰动导致的计算精度问题,根据数值计算理论,可以用矩阵A的条件数cond(A)来衡量[16]
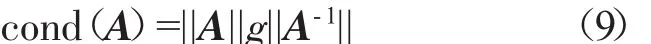
式中:“||||”是矩阵的某种范数。
条件数反映了矩阵A和方程本身的性态,条件数小,扰动引起的解的相对误差小;条件数大,扰动引起的解的相对误差就可能大。理论上,条件数确定了解的相对误差上限,即扰动可引起误差的最大放大倍数。
经以上步骤确定的小偏差方程(4),影响系数矩阵A的性态将对计算结果有直接影响。对此,Urban指出[5],如果测量参数选取较差,将导致故障系数矩阵(FCM)中的系数较大,从而导致方程迭代过程不收敛或者导致较大的计算误差。由此,可以直接通过影响系数矩阵的条件数cond(A)来判断测量参数误差对特征量计算精度的影响。
表1、表3列出了主要几种不同测量参数组合下影响系数矩阵的谱范数||||2条件数。表中符号“×”表示选择该参数。
对表3进行分析:
(1)前面选择的9个测量参数组合的条件数相对7个基本测量参数的条件数较大,即增加测量参数后,区分了3组相关的特征量,使故障定位更有效,同时使方程组(4)的性态变差了,增加了误诊断的可能性。

表3 不同测量参数组合的条件数
(2)测量参数的多少反映了对发动机运行状况的了解程度。从性能监测诊断的角度出发,倾向于合理选择更多的测量参数。但增加测量参数后可能导致方程组(4)的性态变差,如(1)所述,因此具体效果需深入分析。
(3)适当牺牲故障发现性能,即减少预诊断的特征量的数目,可以改善方程组的性态。对于选择的9个测量参数,如果不考虑δηB特征量变化,则计算的条件数只有90.8,方程组的性态得到了很大改善。实际δηB特征量变化有关的燃油喷嘴堵塞故障也可以通过喷嘴前燃油压力或燃油流量等反映出来。因此气路监测诊断时还应综合采用其它监测诊断手段。
(4)适当牺牲故障定位性能,即恰当减少测量参数,可提高方程组(4)的性态。因此在监测诊断时,可减少测量参数的方程组先行判断,提高故障发现性能。在出现易混淆特征量变化,即故障定位性能不够时,再引入更多测量参数的方程组进行判断。
(5)方程组的病态程度是相对的。病态的影响随着计算机字长的增长减轻。病态方程的有效解法可参看相关文献。在消去法的基础上,对已取得的近似解不断改进,就可以达到十分准确的结果。因此,由于测量参数组合导致的诊断误差问题,可以通过改进诊断算法予以弥补。
(6)加入P3.5测量参数,可以使参数组合的条件数减少。因此,如果高温下压力测试可行,可以用参数P3.5代替测试相对困难的N参数,该组合不仅满足诊断的最低数量测量参数要求,而且组合的条件数也相对前面所选9个参数组合的条件数要小得多,数值参见表3。
通过以上对不同测量参数组合下影响系数矩阵的条件数分析,可以认为前述步骤选择的9个测量参数比较符合某3轴舰船燃气轮机的气路监测诊断需求。对于条件数较大的情况,可以采用(3)、(4)或(5)的方法予以改进。该测量参数组合包含了实际发动机控制系统现有的全部5个气路测量参数,实现了最大程度的共享,所以该选择更为优化合理。
6 总结
(1)针对燃气轮机气路性能监测诊断需求,归纳总结了选择气路测量参数的6个要求。
(2)重点利用影响系数、相关系数和条件数,分析了某舰船3轴燃气轮机的气路测量参数的敏感性、相关性和诊断误差,最终选择了适用于气路性能监测诊断的9个测量参数。
(3)该理论方法具有一定的通用性和工程应用价值,对燃气轮机气路测量参数的选择有一定的指导作用。
[1]ИВ.凯巴著.航空燃气涡轮发动机技术诊断[M].王起鹏,刘德磬,译.北京:航空工业出版社,1990:2-5.ИВ.Keba.Aero gas turbine engine technology diagnosis[M].WANG Qipeng,LIU Dexin,translated.Beijing:Aviation Industry Press,1990:2-5.(in Chinese)
[2]Urban L A.Gas path analysis:applied to turbine engine condition monitoring[J].Journal of Aircraft,1973,10(7):400-406.
[3]Urban L A.Parameter selection for multiple fault diagnosis of gas turbine engines [J].Journal of Engineering for Power,1975,97(2):225-230.
[4]Consumi M,Agostino L.A statistical inference approach to gas path analysis of a turbofan[R].AIAA-1998-3551.
[5]Ogaji S O T,Sampath S,Singh R,et al.Parameter selection for diagnosing a gas turbine’s performance deterioration [J].Applied Ener gy,2002,73(1):25-46.
[6]唐耿林.航空发动机性能监视参数选择的研究 [J].推进技术,1998,19(2):38-42.TANGGenglin.Investigationson selectingperformance monitoring pa rameters of aeroengine[J].Journal of Propulsion Technology,1998,19(2):92-96.(in Chinese)
[7]孙祥逢,陈玉春,胡福.发动机故障诊断主因子模型的测量参数选择[J].航空动力学报,2010,25(1):129-135.SUN Xiangfeng,CHEN Yuchun,HU Fu.Research on selection of measurement parameters of engine fault diagnosis based on primary factor mode[J].Journal of Aerospace Power,2010,25(1):129-135.(in Chinese)
[8]范作民,孙春林,白杰.航空发动机故障诊断导论[M].北京:科学出版社,2004:134-138.FANZuomin,SUNChunlin,BAIJie.Introduction toaeroengine fault diagnosis[M].Beijing:Science Press,2004:134-138.(in Chinese)
[9]邓明,金业壮.航空发动机故障诊断[M].北京:北京航空航天大学出版社,2012:95-96.DENG Ming,JIN Yezhuang.Aeroengine fault diagnosis[M].Beijing:Behang University Press,2012:95-96.(in Chinese)
[10]Ogaji S O T.Advanced gas path fault diagnostics for stationary gas turbines[D].Bedford:Cranfield University,2003.
[11]陈益林.航空发动机试车工艺[M].北京:北京航空航天大学出版社,2010:212-215.Chen Yilin.Aeroengine test technology[M].Beijing:Beihang University Press,2010:212-215.(in Chinese)
[12]陈卫,程礼,李全通,等.航空发动机监控技术[M].北京:国防工业出版社,2011:156-159.Chen Wei,Cheng Li,LI Quantong,et al.Aircraft engine monitoring technology[M].Beijing:National Defense Industry Press,2011:156-159.(in Chinese)
[13]LI Yiguang.A GPA diagnostic system for aeroengine applications[J].Journal of Aerospace Power,2007,22(6):898-908.
[14]LI Yiguang.Performance analysis based gas turbine diagnostics:a review[J].Journal of Power and Energy,2002,216(5):363-377.
[15]何汉林,魏汝祥,李卫军.数值分析[M].武汉:湖北科学技术出版社,1999:245-246.HE Hanlin,WEI Ruxiang,LI Weijun.Numerical analysis[M].Wuhan:Hubei Scienceand Technology Press,1999:245-246.(in Chinese)
[16]邓建中,葛仁杰,程正兴.计算方法[M].西安:西安交通大学出版社,1985:50-52.DENG Jianzhong,GE Renjie,CHENG Zhengxing.Calculation method[M].Xi'an:Xi'an Jiaotong University Press,1985:50-52.(in Chinese)
Selection of Gas Path Measurement Parameters for Marine Gas Turbine in Theory
JIANG Rong-jun,GAO Jian-hua,LIU Yong-bao
(College of Power Engineering,Naval University of Engineering,Wuhan 430033,China)
According to the validity demand of gas turbine gas path performance monitoring and diagnosis,requirements for gas path measurement parameters selection were generalized and summarized,and a systematic and complete theoretical method of gas turbine gas path measurement parameter selection was put forward.Based on the preliminary selection with the requirements of measurability,testability and measuring accuracy,the sensitivity,correlation,diagnosis error of the gas path measurement parameters were analyzed in combine with influence coefficient,correlation coefficient and condition number respectively.Finally,the measurement parameters were chosen for the gas path performance monitoring and diagnosis of a marine gas turbine with three shafts.Example shows that the theoretical method has certain universality and engineering application value,and has certain instruction function to the selection of gas path measurement parameters of gas turbine.
gas path;monitoring;measurement;diagnosis;marine;gas turbine
V231.1
A
10.13477/j.cnki.aeroengine.2015.01.015
2013-10-09
姜荣俊(1973),男,博士,研究方向为燃气轮机的状态监测和故障诊断;E-mail:jiang_rj@163.com。
姜荣俊,高建华,刘永葆.舰船燃气轮机气路测量参数的理论选择方法[J].航空发动机,2015,41(1):74-79.JIANGRongjun,GAOJianhua,LIUYongbao.Selection of gaspath measurement parametersfor marinegasturbinein theory[J].Aeroengine,2015,41(1):74-79.
(编辑:赵明菁)

