金属软管在航空发动机上的应用
贾 铎,罗 鹏,邱明星,高 雷
金属软管在航空发动机上的应用
贾 铎,罗 鹏,邱明星,高 雷
(中航工业沈阳发动机设计研究所,沈阳 110015)
针对发动机管路制造偏差和运动位移的补偿要求,对金属软管在航空发动机上的应用进行研究。根据金属软管的系统、结构尺寸、接口参数和位移补偿,采用样条曲线对软管路径进行拟合,并运用有限元求解变形后的路径形状的计算方法对金属软管的长度和补偿工作条件下的曲率半径进行了分析。结果表明:金属软管的管形变化可满足发动机位移补偿要求,并为金属软管在某型发动机上的应用提供依据。
金属软管;航空发动机;位移补偿;曲率半径
0 引言
金属软管具有质量轻、体积小、承压高、耐腐蚀、耐高低温、抗疲劳、柔性好等优点,能够吸收振动,补偿安装偏移和管线位移,广泛应用于航空、航天、船舶和兵器等领域[1-4]。目前在航空发动机上的金属软管多用于补偿制造偏差和热偏差,而补偿较大运动位移在国内的大中型涡喷、涡扇发动机研制中尚未应用[5]。
本文对金属软管在工作时管形变化对位移的补偿能力进行分析和研究。
1 金属软管设计要求
金属软管由网体部分和两端连接接头焊接而成,其中网体又由金属波纹管、接管、环、钢丝网套焊接而成。受金属波纹管的结构限制,金属软管不能过度弯曲和承受轴向载荷,在承受扭曲应力或交变应力时,寿命会大大缩短[6-9]。因此,金属软管需要在发动机上的有限空间内合理安装和固定,同时还要满足运动位移补偿要求,难度较大。
1.1 系统要求
(1)实现发动机和配装飞机附件机匣之间的管路接口连接。
(2)发动机和配装飞机附件机匣共用滑油系统,金属软管实现输送滑油系统工作介质,如图1所示。
1.2 结构尺寸要求
(1)根据某型发动机、飞机附件机匣的空间位置和接口要求,金属软管采用硬管和软管组合结构,通过两端硬管部分将发动机和飞机附件机匣接口之间的空间角度转换为平面角度,使软管柔性部分成为1个平面内1个圆弧结构形式。金属软管的结构尺寸如图2所示。
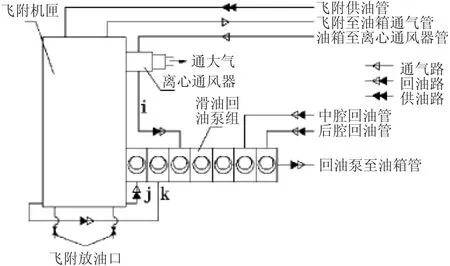
图1 金属软管系统
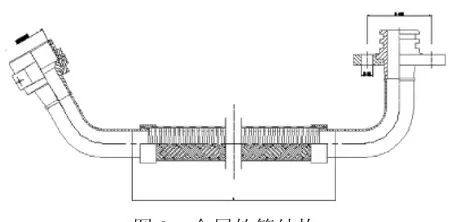
图2 金属软管结构

表2 软管接口位置
(2)根据发动机的系统要求,确定金属软管的规格,见表1。
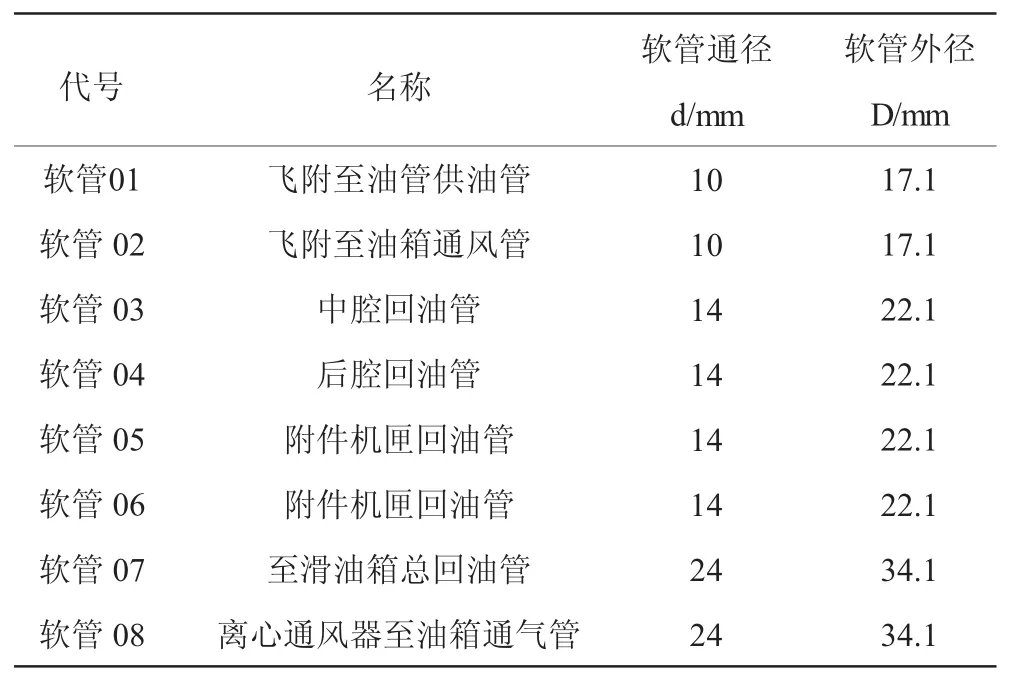
表1 金属软管规格
1.3 接口位置要求
根据发动机数字样机模型,确定金属软管接口位置(对应的接头端面圆心坐标和外法矢量),数据见表2。
表2中坐标及矢量信息对应的基准坐标系如图3所示。取主安装节截面为YZ平面,其与发动机轴线交点为主坐标系原点(0,0),X轴由发动机出口指向进口,且与发动机旋转轴线重合;Z轴为从原点出发的径向线,其正向为指向发动机正上方;Y轴按右手法则确定。
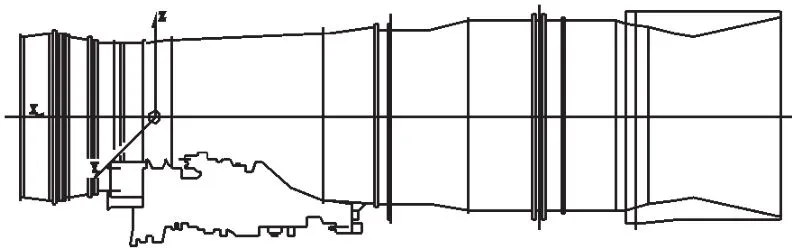
图3 发动机主坐标系
1.4 位移补偿要求
补偿飞机附件机匣与发动机之间相对位移公差。其中相对位移补偿要求为 Δx=0 mm;Δy=±6 mm;Δz=±6 mm。
2 计算方法及步骤
2.1 长度计算
软管的长度计算主要包括2个步骤:软管路径确定和路径长度计算,基于材料力学原理,均匀软管在两端受约束后,其中心线形状应至少满足2阶光滑连续;基于高等数学原理,已知曲线起点、终点的坐标和外切向矢量,可以惟一确定1条3次样条曲线[10-13]。
以表2提供的接头端面圆心坐标为软管的起、终端面圆心坐标,以接头端面外矢量为软管端面内矢量,采用样条曲线对软管路径进行拟合。具体拟合方法为:
(1)以起点为坐标原点O,以起点-终点连线为OX轴建立新的直角坐标参考系,换算出起点、终点在新坐标系下的坐标值(x1,y1,z1)、(x2,y2,z2)以及端面矢量在新坐标系下的值(i1,j1,k1)、(i2,j2,k2)。这一步可在UG等CAD软件中方便实现。
(2)样条曲线方程可写为

通过求式(1)的导数可得曲线的斜率为
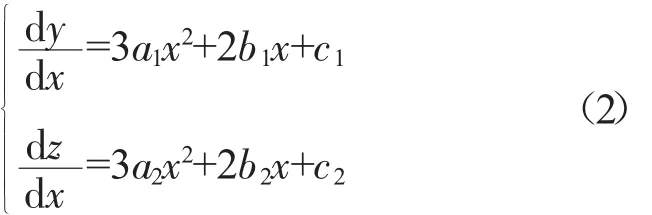
(3)将起点、终点的信息代入式(1)和(2),可得到以a1,b1,c1,d2,a2,b2,c2,d2为未知量的方程组
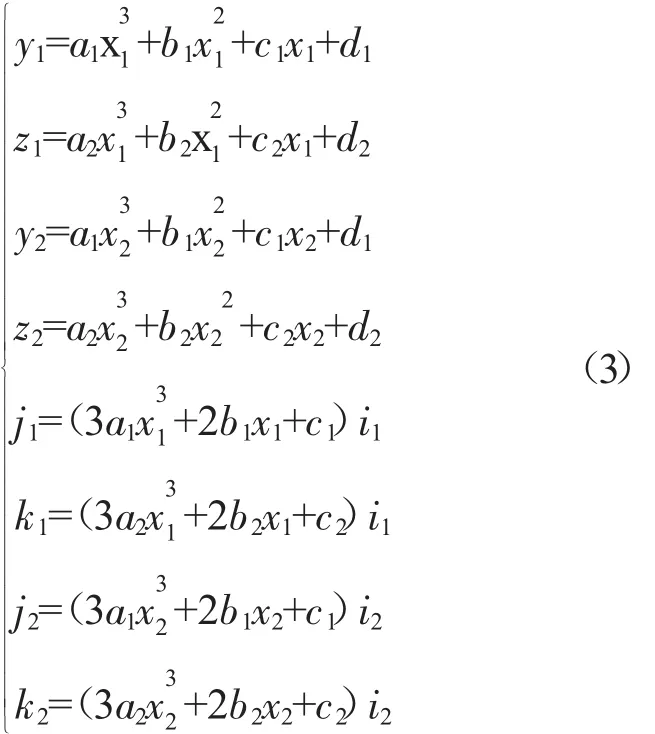
求解式(3)并将结果代入式(1),即得到样条曲线的描述方程。
(4)进行曲线积分计算样条曲线长度l
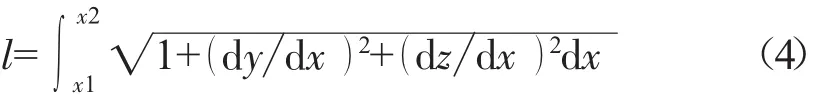
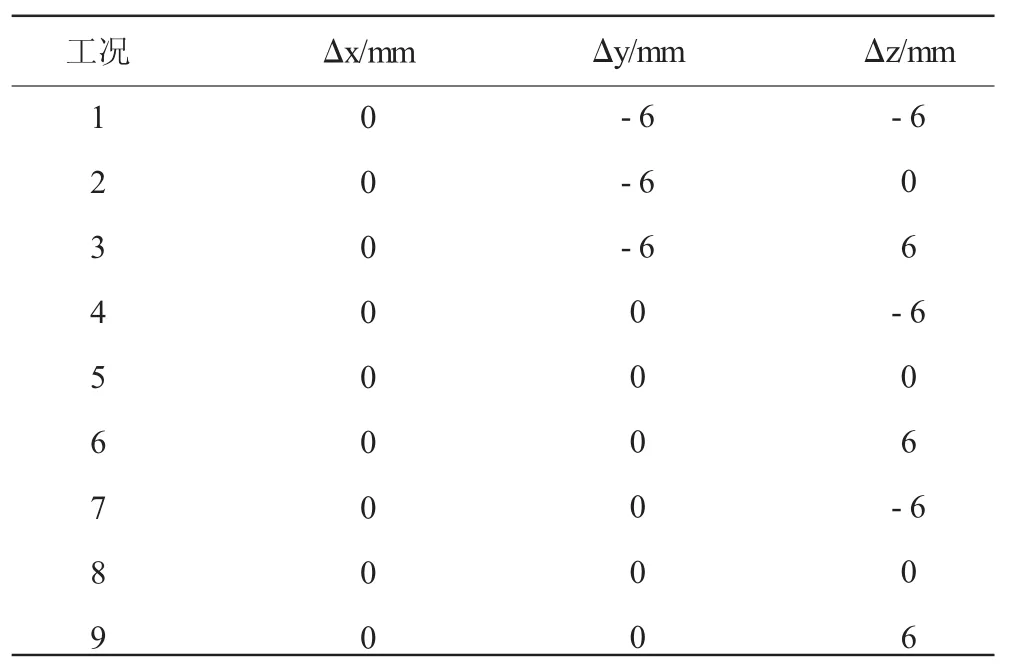
表3 典型极限相对位移变化工况
(5)假定位移补偿,即起点与终点相对位移发生变化时,硬管部分只有平动,而无转动,即起点与终点的端面法矢量不变。计算发生典型极限相对位移变化(即表3所示的9种工况)时,拟合得到的样条曲线的长度,取所有工况中的样条曲线的最大长度为软管设计的基准长度。
计算一端固定,另一端法向矢量不变、而位置在Δy,Δz构成矩形区域内变化时的极限情况下样条曲线的长度,如图4所示。

图4 极限相对位移变化工况
2.2 曲率半径计算
对于式(5)描述的曲线,可看作某一动点的运动轨迹,则该动点

运动速度和加速度矢量为
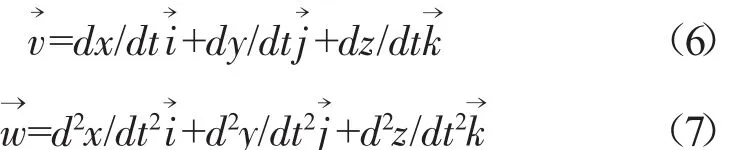
对于有显式表达式的曲线,可直接求其导数进而获得速度与加速度信息,在只有曲线坐标信息时,可采用有限差分的方法进行求解[14-15]。
由运动学中的惠更斯定理,加速度与速度满足
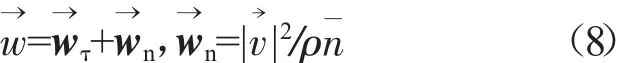
所以有
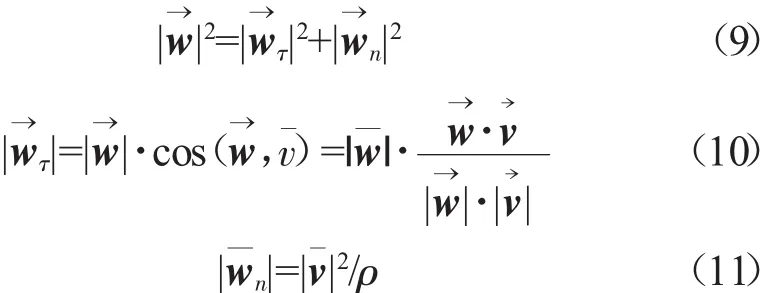
通过式(9)、(10)和(11)即可求解出曲率半径 ρ。
对于按某一工况进行样条曲线拟合得到路径的软管,在其它位移补偿工况时,软管形状必然发生改变,曲率半径也发生改变。本文采用有限元法对其他工况下的变形进行计算(如图5所示)。软管分析建模采用了以下假设:
(1)相对于软管管体,管接头及相关组件刚性较大,假定在位移补偿中,接头端面只有平动,而无转动。
(2)软管内波纹管的波长相对其长度为小值,壁厚较薄,而网套沿长度方向较为均一,假定软管管体截面惯性距沿其长度方向均匀分布。
具体实施步骤为:
(1)建立软管在样条曲线工况下的路径曲线模型;
(2)采用管单元对路径曲线进行单元划分;
(3)输入管截面尺寸参数和材料信息;
(4)一端进行完全零位移约束,另一端按补偿工况要求的位移值施加平动位移,并约束转动位移;
(5)进行几何非线性求解。

图5 有限元求解变形后的路径形状
从有限元计算结果中提取位移变形信息,并计算变形后的路径坐标,然后基于前述方法进行曲率半径的计算。
3 计算结果及分析
3.1 长度计算结果
软管长度计算结果见表4。其中l_hose为按样条曲线拟合计算的软管长度,dis_max为所有极限位移补偿工况下软管起点与终点之间最大直线距离。
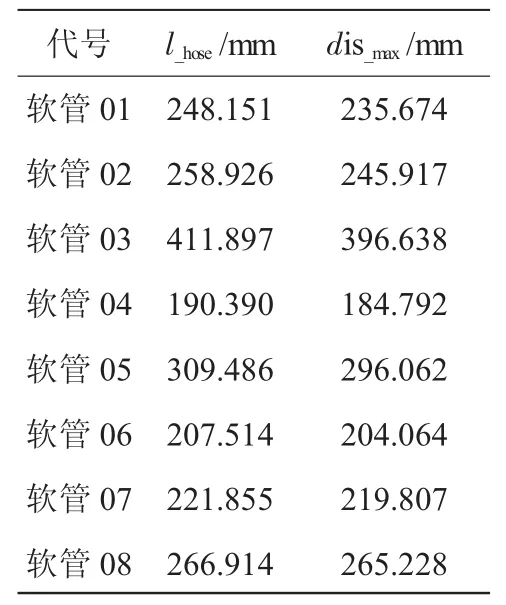
表4 软管长度计算结果
软管实际长度的取值,无疑不能小于表4中的dis_max(起点、终点最大间距),过长则会出现长度“冗余”而导致曲率半径偏小,也容易引起振幅偏大相互碰摩。
3.2 曲率半径计算结果
软管曲率半径的计算结果见表5。其中“安装状态”是指无位移补偿即Δx=Δy=Δz=0的情形;“最小R状态”是指在所有极限位移补偿工况中,平均曲率半径最小的情形;R表示软管路径上的平均曲率半径;R、D_ratio分别为软管路径曲率半径与软管外径的比值。
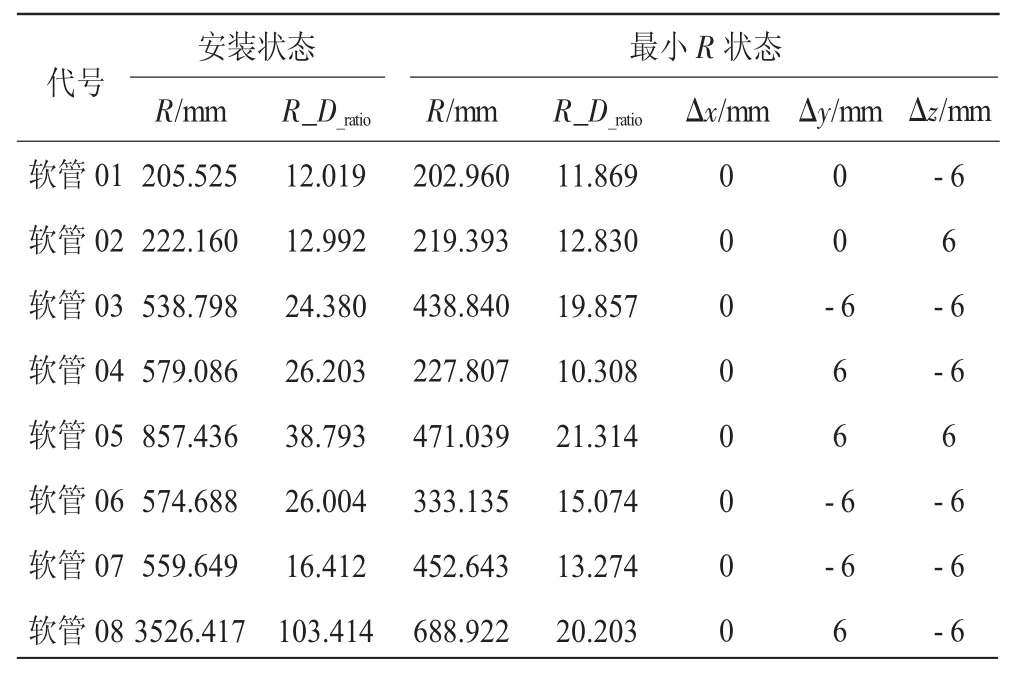
表5 软管曲率半径计算
4 结束语
(1)在某型发动机金属软管设计时,从结构、工艺等方面继承现役金属软管的成熟技术,降低研制风险。
(2)金属软管长度和静态弯曲半径满足在发动机上的安装和固定要求;工作时的最小曲率半径符合动态弯曲半径要求。
(3)金属软管能够满足发动机的位移补偿要求。
[1]吴翠萍,王宁涛.船舶管路金属软管接头选型及安装[J].广船科技,2006(3):33-35.WU Cuiping,WANG Ningtao.Type select and installation of flexible metallic tube joint on vessel[J].Journal of GSI Shipbuilding Technology,2006(3):33-35.(in Chinese)
[2]张文良,王世杰,夏建满,等.一种高压双层金属软管的研制[J].机械设计与制造,2010(1):130-131.ZHANG Wenliang,WANG Shijie,XIA Jianman,et al.Development of high pressure double layer metal hoses[J].Machinery Design and Manufacture E,2010(1):130-131.(in Chinese)
[3]李俊昇,文放.航空发动机管路件标准化的整体构思[J].航空标准化与质量,2010(1):8.LI Junsheng,WEN Fang.Overall conception of aeroengine piping and fitting standards[J].Aeronautic Standardization and Quality,2010(1):8.(in Chinese)
[4]刘凯兰.金属软管的焊接[J].技术与市场,2013,20(12):86.LIU Kailan.Welding of metallic flexible hose[J].Technology and Market,2013,20(12):86.(in Chinese)
[5]葛子余.金属软管[M].北京:宇航出版社,1985:41-52.GE Ziyu.The metal hose[M].Beijing:China Astronautic Publishing House,1985:41-52.(in Chinese)
[6]李新德,王丽.浅谈液压系统软管的使用和维护 [J].机床与液压,2008(8):195-196.LI Dexin,WANG Li.Introduction to the use and maintenance of the metal hose in the hydraulic system[J].Machine Tool and Hydraulics,2008(8):195-196.(in Chinese)
[7]韩淑洁,孙化栋.金属软管网套平衡编织角的研究[J].机械工程与自动化,2007(3):137-139.HAN Shujie,SUN Huadong.Research on the best knitted angle of the metal hose nets[J].Mechanical Engineering and Automation,2007(3):137-139.(in Chinese)
[8]闫松,谭永华,陈建华.高压金属软管应力及参数敏感度分析[J].火箭推进,2013,39(5):76.YAN Song,TAN Yonghua,CHEN Jianhua.Stress and parameter sensitivity analysis of high-pressure metal hose[J].Journal of Rocket Propulsion,2013,39(5):76.(in Chinese)
[9]卢秀荣.浅议金属波纹管膨胀节的力学特性、主要类型与工程应用[J].化工设备与管道,2010,47(2):23-25.LU Xiurong.Discussion of main type,mechanical behavior and application of metal bellow expansion joint[J].Process Equipment and Piping,2010,47(2):23-25..(in Chinese)
[10]盛冬平,朱如鹏,王心丰,等.基于ANSYS的金属软管的动态有限元分析[J].机械设计与制造,2007,24(1):20-21.SHENG Dongping,ZHU Rupeng,WANG Xinfeng,et al.Dynamic finite element analysis of metallic hose based on ANSYS[J].Machinery Design and Manufacture,2007,24(1):20-21.(in Chinese)
[11]盛冬平,朱如鹏,王心丰,等.基于ANSYS的金属软管的静态有限元分析[J].压力容器,2007.24(1):32-35.SHENG Dongping,ZHU Rupeng,WANG Xinfeng et al.Static finite element analysis of metallic hose based on ANSYS[J].Pressure Vessel Technology,2007.24(1):32-35.(in Chinese)
[12]谢传锋,王琦.理论力学[M].北京:高等教育出版社,2009:32-36.XIE Chuanfeng,Wang Qi.Theoretical mechanics[M].Beijing:Higher Education Press,2009:32-36.(in Chinese)
[13]龚曙光,谢桂兰.ANSYS操作命令与参数化编程[M].北京:机械工业出版社,2004:26-29.GONG Shuguang,XIE Guilan.Operation command and parametric programming of ANSYS[M].Beijing:China Machine Press,2004:26-29.(in Chinese)
[14]盛冬平,朱如鹏,王心丰,等.基于ANSYS的金属软管的瞬态有限元分析[J].压力容器,2008,25(1):14-17.SHENG Dongping,ZHU Rupeng,WANG Xinfeng et al.Transient dynamic finite element analysis of metallic hose based on ANSYS[J].Pressure Vessel Technology,2008,25(1):14-17.(in Chinese)
[15]韩淑洁.基于ANSYS的金属软管参数化有限元建模方法[J].制造业自动化,2011,33(21):57-59.HAN Shujie.The method of building parametric finite element modeling of metal hose based on ANSYS [J].Manufacturing Automation,2011,33(21):57-59.(in Chinese)
Application of Metal Hose for Aeroengine
JIA Duo,LUO Peng, QIU Ming-xing,GAO Lei
(AVIC Shenyang Engine Design and Research Institute,Shenyang 110015, China)
To meet the compensation requirements for pipe manufacturing deviations and movement displacement of the engine,the application of the metal hose for aeroengine was investigated.According to metal hose of system,structure size,interface parameter and displacement compensation requirements,the hose path was fitted by spline curve.The length of metal hose and curvature radius at compensation work conditions were analyzed by the path shape calculation method of ANSYSfinite element solving deformation.The results show that the tube style changes of the metal hose can meet displacement compensation requirements of engine and provide reference for application of metal hose for an aeroengine.
metal hose;aeroengine;displacement compensation;curvature radius
V232.7
A
10.13477/j.cnki.aeroengine.2015.01.007
2013-01-10 基金项目:航空动力基础研究项目资助
贾铎(1980),男,工程师,主要从事航空发动机外部结构设计工作;E-mail:jiaduo1980326@tom.com。
贾铎,罗鹏,邱明星,等.金属软管在航空发动机上的应用[J].航空发动机,2015,41(1):36-40.JIA Duo,LUOPeng,QIU Ming-xing,et al.Application of metal hosefor aeroengine[J].Aeroengine,2015,41(1):36-40.
(编辑:沈广祥)

