Continuities of Progressive and MixingAlgorithm for Surface Modeling and Editing
LIU Yukun(刘玉坤)
1School of Information Science and Engineering,Hebei University of Science and Technology,Shijiazhuang 050018,China
2Institute for Research of Applicable Computing,University of Bedfordshire,Luton LU1 3JU,UK
Introduction
The progressive and mixing algorithm (PAMA)is first presented in the author's thesis[1].The PAMA is a novel method of surface modeling and editing.
In computer graphics,there are many researches involved,such as geometric algorithms of construction and edition of curves and surfaces,lighting,texturing,2Dand 3D rendering technologies, and human-computer interactions[2-6].The surface modeling and editing is one of the most active branches of researches in computer graphics.The algorithms of surface modeling and editing have been applied to other relevant fields,these being computer-aided design (CAD) and computer-aided geometric design(CAGD).They have played a very important role in industry designs of cars,ships,airplanes,etc.
In the surface modeling and editing,one can use a variety of splines to fit varied shapes of curves and surfaces for design purposes.Among the splines,the fundamental and popular ones are Bézier-splines and B-splines.Béziersplines have many good geometric properties,for example,the convex hull property,variation-diminishing property,and convergence.
A problem of Bézier-splines is that the degree of the Bézier curve or surface is dependent directly on the number of vertices of the Bézier polygon.This problem leads to the global characteristics of the Bézier control points,that is,each control point has an effect on the entire shape of the Bézier curve or surface.When a control point is moved,the entire shape of the Bézier curve or surface will be unexpectedly changed.
To solve this problem,B-splines are used.B-splines are defined locally.That is,changes in one of control points affect the corresponding curve segment or surface patch locally without influences on other parts.This merit is very useful in practical designs,such as CAD and CAGD.However,it cannot meet the design needs only to change the positions of control points because these changes are limited.In real designs,one requires more control on shapes of curves and surfaces.For this reason,many more variants of splines,such as Beta-splines(orβ-splines),ν-splines,and τ-splines,are invented[7].They can improve the freedom of control on shapes of curves and surfaces and maintain the continuities of curvature or torsion of them.
1 Related Studies
For a curve,the basic idea of splines is to divide the given curve into smaller intervals, and form an approximating curve consisting of pieces of curve segments.As regards a surface,the similar idea is to split the given surface into smaller patches,and construct an approximating surface composed of pieces of surface patches.In this way,the splines curve or surface can replace the original curve or surface in a design.The former is usually easy to be modeled and changed for design purpose while the latter is not practical to be controlled for the same purpose.Since the global smoothness is necessary for the approximating curve or surface,the piecewise curve or surface must be concerned with continuities between two adjoined segments or patches.Let us first explore two types of continuities,parameter continuities and geometric continuities.
1.1 Parameter continuities and geometric continuities
Since splines are represented with spline functions,a curve or surface constructed with splines can be represented with parameter polynomials.A Bézier curve of degree nis written in a Bernstein polynomial form with one parameter as

where uis the parameter and takes a value 0≤u≤1,biare the control points,and(u)are Bernstein polynomials and(u)=()n i ui(1-u)n-i.A Bézier surface of degree(m,n)is expressed in a Bernstein polynomial form with two parameters as

where uand v are the parameters and take values 0≤u,v≤1;bi,jare the control points;(u)and(v)are Bernstein polynomials,(u)=( )m i ui(1-u)m-iand
With parameter expressions,it is natural for piecewise curves and surfaces to have parameter continuities.Given two parameter curves,s(u),u ∈[u0,u1],and t(w),w∈[w0,w1],they meet at a common point P =s(u1)=t(w0).The conditions of k-order parametric continuities(Ck)at this common point are written as
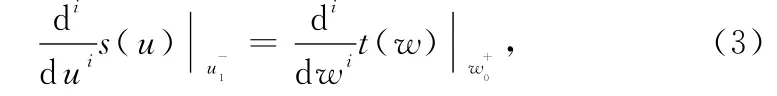
where u1=w0and i=0,1,…,k.This equation means that the k-order derivative of s(u)with respect to uat u1is equal to the k-order derivative of t(w)with repect to wat w0and u1=w0.
According to studies of Hoschek and Lasser[7],and Farin[8],the zero-,the first-,and the second-order geometric continuities(G0,G1,and G2)are expressed as follows,

and


Compared with conditions of C0,C1and C2of Eq.(3)with i =0,1,and 2,conditions of G0,G1and G2of Eqs.(4),(5)and(6)are less restricted.Because conditions of parameter continuities are more constricted,some splines curves that do not meet these conditions can meet the conditions of the corresponding geometric continuities.Curves that meet the specific-order geometric continuity can provide a special visual smoothness,which can meet most design needs.For this reason,Beta-splines[9]are used to construct curves with two more degrees of shapemanipulation freedom by changing two shape parameters,β1andβ2,than Bézier-splines and B-splines.
1.2 Beta-splines
In Ref.[9],the authors use three conditions of Eqs.(4),(5)and(6)to join two neighboring curve segments to form a piecewise curve that meets the geometric continuities of G0,G1and G2.This curve is called Beta-splines curve.Its benefit is of adding two more degrees of freedom to shape changes than that of changing only positions of control points.In addition,two shape parameters,β1andβ2,of each control point can be changed independently,and they have distinct effects on the curve shape.By increasingβ1of a control point,the curve can bias along the arc direction at the control point.By increasingβ2of the control point,the curve can approach the control point.These merits equip designers with more tools to manipulate the curve shapes for their design purpose.
1.3 Composite surfaces
Like a piecewise curve that is formed with splines in different intervals and by joining them together with geometric continuity conditions,a composite surface can be constructed by joining splines patches with the conditions of geometric continuities on the common boundaries between different patches[7-8].An example of composite surfaces is a composite bi-cubic Bézier-splines surface.Each patch of the composite bi-cubic Bézier-splines surface is a tense product of two cubic Bézier-splines curves as follows

where 0≤u,v ≤1,and bi,jare the control vertices.
The tense product of two splines curves can,however,lead to a large amount of multiplication operations during the computing of algorithms for surface modeling and editing.This must be noticed because the applications of algorithms for surface modeling and editing must meet the needs of practical designs,such as CAD and CAGD,which cannot tolerate a slow processing caused by a large amount of multiplication computing.
With the merits mentioned above,Beta-splines have been used to construct piecewise curves[9].A special case of Beta-splines curves is a piecewise cubic Bézier-splines curve,which is formed by joining two cubic Bézier-splines curve segments with meeting the G2conditions on the common points between any two neighboring segments[9-11].
In Eq.(7),two parameterizations,u and v,are involved.Intuitively,a composite bi-cubic Bézier-splines surface with Beta-constraints should involve four shape parameters,two for each parameterization.They should be βu1andβu2for u parameterization andβv1andβv2for v parameterization.
Beta-splines are also used to construct two special cases of composite surfaces by researchers[12-13].In Ref.[12],the authors take the same shape parameters in two parameterizations for each control point.In Ref.[13],one of the shape parameters(βu2)takes one for all control points so that the computing is decreased but the control on these parameters is no use.
To retain the control of all four shape parameters with a limited amount of computing,the PAMA is presented for surface modeling and editing[1].To make it palpable,an introduction of the construction scheme of PAMA is presented in the next section and the continuities of PAMA will be discussed in section 3.
2 Construction Scheme of PAMA
Given a set of original control points P(i,j),a composite bi-cubic Bézier-splines surface can be constructed with the PAMA.The constructed mesh is composed of a set of vertices Q(l,k),which consists of four times vertices more than those of the set of P(i,j),as shown in Fig.1.Each patch is a bi-cubic Béziersplines patch with four original control points and sixteen constructed points.As shown in Fig.1,the patch of si,j(u,v)consists of four original control points[P(i,j),P(i+1,j),P(i+1,j+1),P(i,j+1)]and sixteen constructed points[Q(3i,3j),Q(3i+1,3j),Q(3i+2,3j),Q(3(i+1),3j),Q(3i,3j+1),Q(3i+1,3j+1),Q(3i+2,3j+1),Q(3(i+1),3j+1),Q(3i,3j+2),Q(3i+1,3j+2),Q(3i+2,3j+2),Q(3(i+1),3j+2),Q(3i,3(j+1)),Q(3i+1,3(j+1)),Q(3i+2,3(j+1)),Q(3(i+1),3(j+1))].

Fig.1 A patch si,j(u,v)with original control points,P(i,j),and the constructed vertices,Q(l,k)(patches and vertices are identified at the points of the corresponding lower-left corners)
To avoid the large computing cost of multiplication,the PAMA does not generate the constructed points Q(l,k)directly with a tense product of two Beta-splines.Instead,the PAMA generates points for each patch that is a bi-cubic Bézier-splines patch and joins these patches with constrains on their common boundaries.
The PAMA adopts a scheme to generate different points of a patch(or mesh,say Q(l,k),as shown in Fig.1)from an original patch(say P(i,j),as shown in Fig.1)with different strategies.
2.1 Points on common boundaries
Common boundaries are along u or v direction,respectively,and isoparametric curves of a Bézier-splines surface,as shown in Fig.1.These curves can keep the second-order geometric continuities by setting the special conditions on their second-order partial derivatives.Along the u direction,they are

and
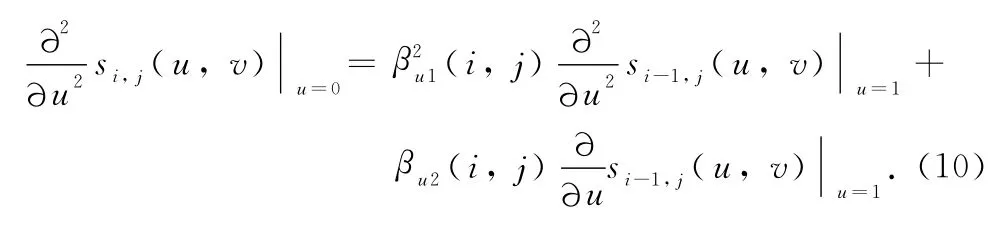
Along the v direction,they have the similar equations as Eqs.(8)-(10).With these equations,we can construct the points on the common boundaries as follows

and

2.2 Points on corners
For points on corners,twists,the mixed partial derivativesare considered.Along with twists are twist vectors.Let us inspect Q(3i,3j)that is a corner point of four patches,si,j(u,v),si-1,j(u,v),si,j-1(u,v)and si-1,j-1(u,v),as shown in Fig.2.

Fig.2 A point at the corner,Q(3i,3j),with relative patches and points
Take si,j(u,v)as an example.According to Ref.[8],the twist vector at Q(3i,3j)is the deviation of the corner sub-quadrilateral formed with Q(3i,3j),Q(3i+1,3j),Q(3i+1,3j+1),and Q(3i,3j+1)from the tangent plane at this corner.Four adjoining patches meeting the condition of the first-order parametric continuity have the same twist at the corner[8].This condition is so restrictive to limit the shape changes around the corner.Therefore,the PAMA does not use this condition to construct the points at corners,but blends the effects of the control points along u and v directions into one equation with the linear interpolation as follows,
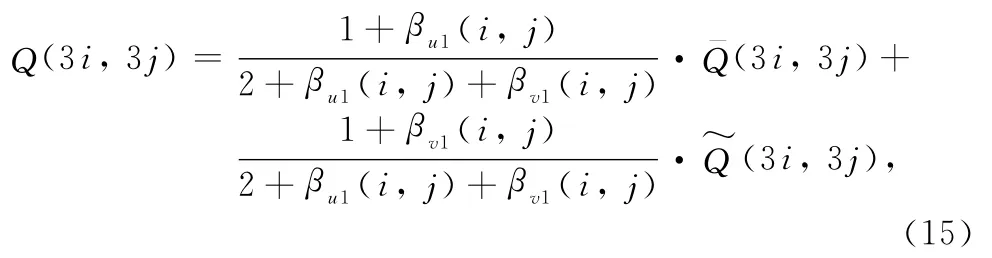
where
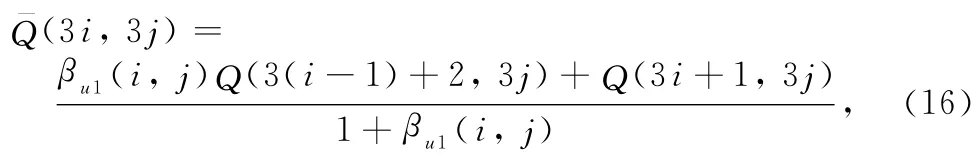
and

2.3 Inside points
As shown in Fig.1,four inside points in the patch si,j(u,v)are Q(3i+1,3j+1),Q(3i+2,3j+1),Q(3i+1,3j+2),and Q(3i+2,3j+2).To maintain the freedom of changing four shape parameters,βu1,βu2,βv1,andβv2,independently,the PAMA blends the variations of points along both uand v directions with the method presented in studies[9-11]and the bisection interpolation.The equations are written as follows

3 Continuities of PAMA
Through the construction process of PAMA discussed in section 2,we can summarize the continuities of PAMA.
(1)Inside any bi-cubic Bézier-splines patch,si,j(u,v),it meets the C2conditions.
(2)Along the common boundary curves between two neighboring patches,the C0(and G0)condition is met.
(3)Along the u-and v-isoparametric curves in a composite surface constructed with PAMA, the G2conditions are met approximately.
(4)The first partial derivatives agree along the common boundary curve between two neighboring patches.
4 Conclusions
The PAMA provides a new scheme for surface modeling and editing.It gives designers four more degrees of freedom to manipulate a 3Dobject for design purpose.In addition,the benefits from the PAMA can be listed as follows(details and more examples of applications can be referred to the thesis[1]).
(1)Medium continuous conditions on the common boundaries are rewarded with more types of shapes.For example,a shape fold that cannot be generated under G2or G1is formed with PAMA,as shown in Fig.3.Figures 3(a)and 3(b)show the examples of G0while Figs.3(c)and 3(d)are the examples of G2.

Fig.3 A clamshell box(a-b)and ashtray(c-d)constructed with PAMA:(a)the connection side marked with the black arrow is G0in the v direction;(b)the same box as(a)viewed in a different angle;(c)the dent marked with the black arrow is G2;and(d)the same ashtray as(c)viewed in a different angle
(2)The effects of changing four shape parameters,βu1,βu2,βv1,andβv2,are distinguishable.
(3)They retain the effects of the corresponding Betasplines curves[9].That is,changingβu1(i,j)orβv1(i,j)can make the surface bias locally around the P(i,j)point.Changingβu2(i,j)orβv2(i,j)can make the surface approach locally to the P(i,j)point.
(4) The effects of shape parameters keep the orientation sense.Changingβu1orβu2makes shape changing along the u direction while varyingβv1orβv2makes shape changing along the v direction.
[1]Liu Y K.A Novel Parallel Algorithm for Surface Editing and Its FPGA Implementation[D].Luton,the UK:University of Bedfordshire,2013:135-155.
[2]Zhang J Q,Shi Z.Triangulation of Molecular Surfaces Based on Extracting Surface Atoms[J].Computers & Graphics,2014,38:291-299.
[3]Wedel A,Badino H,Rabe C,et al.B-Spline Modeling of Road Surfaces with an Application to Free-Space Estimation[J].IEEE Transactions on Intelligent Transportation Systems,2009,10(4):572-583.
[4]Kim K,Lepetit V,Woo W.Real-Time Interactive Modeling and Scalable Multiple Object Tracking for AR[J].Computers&Graphics,2012,36(8):945-954.
[5]Park Y,Lepetit V,Woo W.Handling Motion-Blur in 3D Tracking and Rendering for Augmented Reality [J].IEEE Transactions on Visualization and Computer Graphics,2012,18(9):1449-1459.
[6]Ben-Artzi A,Egan K,Durand F,et al.A Precomputed Polynomial Representation for Interactive BRDF Editing with Global Illumination[J].Transactions on Graphics,2008,27(2):Article No.13.
[7]Hoschek J,Lasser D.Fundamentals of Computer Aided Geometric Design [M].Wellesley, Massachusetts:A K Peters,Ltd.,1993:217-243.
[8]Farin G.Curves and Surfaces for Computer Aided Geometric Design,a Practical Guide[M].3rd ed.New York:Academic Press Inc.,1993:201-285.
[9]Barsky B A, DeRose T D.Geometric Continuity of Parametric Curves: Constructions of Geometrically Continuous Splines [J].IEEE Computer Graphics and Applications,1990,10(1):60-68.
[10]Farin G.Visually C2 Cubic Splines[J].Computer Aided Design,1982,14(3):137-139.
[11]Boehm W.Curvature Continuous Curves and Surfaces[J].Computer Aided Geometric Design,1985,2(4):313-323.
[12]Barsky B A,DeRose T D.The Beta2-Spline:a Special Case of the Beta-Spline Curve and Surface Representation[J].IEEE Computer Graphics and Applications,1985,5(9):46-58.
[13]Joe B.Knot Insertion for Beta-Spline Curves and Surfaces[J].ACM Transactions on Graphics,1990,9(1):41-65.
——首批全国岗位学雷锋标兵刘玉的故事
 Journal of Donghua University(English Edition)2015年2期
Journal of Donghua University(English Edition)2015年2期
- Journal of Donghua University(English Edition)的其它文章
- Two Types of Adaptive Generalized Synchronization of Chaotic Systems
- Exploring Mobile LearningTools Used in Autonomous Learning:a Perspective from China
- Optimal Packet Size of Underwater Sensor Networks
- A Fast Bayesian Evaluation Algorithm Based on the Second Categoryof Maximum Likelihood
- Dynamic Simulation Analysis of the Flexible SwapDevice
- Design of Control and Monitor System Applied in Artificial Grass Tufting Machine
