Effects of Fiber Volume Fraction on Damping Properties of Three-Dimensional and Five-Directional Braided Composites

GAO Yan (高 岩) ，LI Jia-lu (李嘉禄)

Composites Research Institute of Tianjin Polytechnic University，Tianjin 300387，China

Introduction

The vibration phenomenon is often encountered when composite materials are in use.Because the vibration could cause resonance or fatigue of composite materials，the natural frequency and mode performance of composite materials must be understood in the design of composite products.Three dimensional (3D) braided composites have the integrated structure，in which the fiber tows interweave together to form a net and no-laminar structure.So it has many good properties，such as higher specific strength and specific stiffness，higher temperature resistance，and better vibration performance.

The research from Dion et al.［1］investigated the damping level trends of 3D braided composites as a function of matrix material， fiber-matrix interface， fiber braid angle， fiber volume，and axial fiber tow size.The logarithmic decrement of braided composite was considerably larger than steel specimen.Trends of increasing damping were measured with both increasing fiber braid angle and fiber volume.Dynamic mechanical characteristics of carbon fiber/epoxy braided structural reinforced composites were studied［2］by means of the experimental modal analysis technique.By comparing with steel beam and tube，the results revealed that braided structure composite had a better dynamic mechanics behavior.The experimental study from Li［3］showed that the damping properties for the five-directional braiding structure were superior to the four-directional braiding structure.Lu et al.［4］studied the vibration properties of 3D four-directional and fivedirectional braided composites by the theoretical analysis.The calculation results indicated that the first order natural frequency increased with fiber volume fraction and decreased with braiding angle.Works［5-9］on vibration property of braided composites components have been done and the vibration property is affected by the reinforcement's parameters.

General theoretical approaches are not capable of accurately predicting the complex dynamic response of braided composites［10］.In this report，an experimental modal testing method for carbon fiber/resin three-dimensional and fivedirectional (3D-5Dir)braided composites cantilever beam was used.The free vibration responses，as well as the first three orders of natural frequency and damping ratio of the braided composites are studied.The vibration characters of braided composites with different fiber volume fraction are discussed.Meanwhile，the experimental modal analyses of carbon fiber plain woven laminated/epoxy resin composite cantilever beams with different fiber volume fraction are concerned for comparison.

1 Experimental

In this study，the single-input and single-output (SISO)modal testing of cantilever beam was used to accurately predict the free vibration property of 3D-5Dir braided composites with different fiber volume fraction.Meanwhile，modal tests of carbon fiber Plain woven fabric/epoxy resin laminated composites with different fiber volume fraction were also finished，in order to make modal properties comparison between 3D-5Dir braided composites and laminated composites.

1.1 Specimens preparation

The fiber tow，used for 3D-5Dir braided performed with different fiber volume fraction，was T700-12K carbon fiber and the matrix was TDE86 epoxy resin.The braided performs had integral structures，and each was directly braided to form a three-dimensional sheet fabric with the size of 25 mm (width)×250 mm (length) ×4 mm (thickness)and different fiber volume fraction.The formation technology of braided composite specimens was the net-shape forming technique of resin transfer molding (RTM)technology with a specific mold，which can keep the integral structure and make a high quality surface of specimens.

The reinforment of laminated composites was woven plain fabric (500 g/m2)with T700-12K carbon fiber tows as warp yarn and weft yarn.The resin used was TDE-86 epoxy resin.The formation technology of laminated composite was also RTM technology.However，the laminated composites were formed as the size of 400 mm × 600 mm × 4 mm for several pieces firstly，then the large piece of laminated composites was cut into many small pieces with the size of 25 mm (width)×250 mm(length)×4 mm (thickness)as specimens for testing and the length direction of specimen was along the warp direction of reinforcement.The parameters of specimens are given in Table 1.In Table 1，B represents 3D-5Dir braided composites and L represents laminated composites.The definition of braiding angle can be found in Ref.［10］.

Table 1 The parameters of specimens

Two strengthening plates were affixed to the two sides of clamped end of the specimen by using epoxy glue films(J-47A，cured at 120 ℃and 0.25 GPa pressure for 2 h)，in order to provide a clear cantilever boundary and prevent from damaging the specimen when specimen was clamped in the rigid fixture during the test.The strengthening plate was aluminum piece with the size of 25 mm (length)×25 mm (width)×2 mm(thickness).The specimen with strengthening plates is shown in Fig.1.

Fig.1 The appearance of the composites specimen

1.2 Modal testing procedure

A simple experimental setup was used to measure the free vibration response of cantilever beams，shown in Fig.2.It consisted of rigid test fixture，excited hammer with force sensor，accelerometers，filter amplifier，AD converter，and computer data acquisition system.Before the test，all of the specimens were subjected to room temperature of 23 ℃，so as to make them stability in thermodynamic property.To simulate cantilever boundary condition，the end with strengthening plates of specimen was mounted in a massive rigid fixture which could provide a horizontal support.The effective dimensions of the cantilever beam were 25 mm (width)×225 mm (length)×4 mm (thickness).A miniature pick-up accelerometer(LC0408T，Beijing Wavespectrum ＆ Science ＆ Technology Co.，Ltd.，China)，weighing 2.8 g and having a sensitivity of 4.4 pc/g，was attached nearly to the free end of the cantilever.The impulse hammer was used to induce the excitation of the vibrations of the sample.This product had advantage on exciting multi-order resonances at one time.The impulse width in the frequency domain was controlled by the stiffness of the hammer head.Specimen was excited near the root end，and a force transducer (BZ1201，Beijing Wavespectrum ＆Science ＆Technology Co.，Ltd.，China)was positioned at the hammer to obtain the excitation signal as a function of time.The input force signal and the output acceleration signal were fed to a dual channels power amplifier(WS2401，Beijing Wavespectrum ＆Science ＆ Technology Co.，Ltd.，China)，AD converter(WS5921，Beijing Wavespectrum ＆ Science ＆ Technology Co.，Ltd.，China)，and then analyzed by a PC computer using the modal software (Vib' SYS modal analysis system)to get the first three modal parameters (frequency response function，natural frequency，and damping ratio)of the beam.

2 Results and Discussion

In order to analyze the relationships that between the vibration properties of braided/laminated composites and fiber volume fraction，the composite specimens were tested group by group according to the magnitude of fiber volume fraction.The results obtained and analyses considered are reported as follows.

2.1 Experimental results of braided composite specimens

The vibration properties of braided specimens with different fiber volume fraction were tested and then analyzed by the modal experimental analysis method.Modal parameters were derived.The modal test results of braided composite specimens with different fiber volume fraction are given in Table 2.It indicates that the first three modal parameters of braided composite specimens change obviously when its fiber volume fraction changes.Therefore，in the condition of fixed braiding angle，fiber volume fraction plays an important part in the vibration properties of the braided composites.As the group of B-A1(braiding angle α is 21°)，the first order natural frequency increases，and the first order damping ratio decreases，when fiber volume fraction increases from V1 (the fiber volume fraction is 45.30%)to V3 (the fiber volume fraction is 64.27%).The relations are agreed well with the studies in Refs.［3-4］.In this study，it is approved that all the first three orders of results comply with those relations and more details are achieved.

Table 2 The first three modal factors of braided composites (average)

The natural frequency and fiber volume fraction have a significant proportional relation，while the damping ratio and fiber volume fraction have an inverse relation.Moreover，with the same braiding angle and fiber volume fraction，the natural frequency increases gradually from the first order to the third order.The higher natural frequencies indicate higher resistant to deformation under impact exciting，which means the higher stiffness and smaller deformation factor.The higher natural frequency makes the resonance difficult to excite.However，the relationship between damping ratio and fiber volume fraction is contrary to that between natural frequency and fiber volume fraction.The damping ratio decreases from the first order to the second order，and then increases in the third order，with the maximum value at the first order.The higher damping ratio obtained more energy absorption and faster energydecay.From above，it can be concluded that fiber volume fraction is a very important factor to determine the vibration performance of 3D-5Dir braided composites.

2.2 Normalized analyzing for natural frequency and damping ratio of braided composite specimens

The normalized analyzing method is the method to derive the ratio of any frequency or damping ratio to the maximum frequency or the maximum damping ratio with the same order，They are the dimensionless values and can release the changing rates of curves more distinctly and intuitively in comparison.

Figures 3-5 derive the relations between fiber volume fraction and the normalized frequency of the first three order frequencies of 3D-5Dir braided composites with different braiding angles(A1，A2，and A3).The curves indicate that the natural frequency dramatically increases with the increase of fiber volume fraction in each mode，and the increasing degree rates become smaller when fiber volume fraction is about 55%.

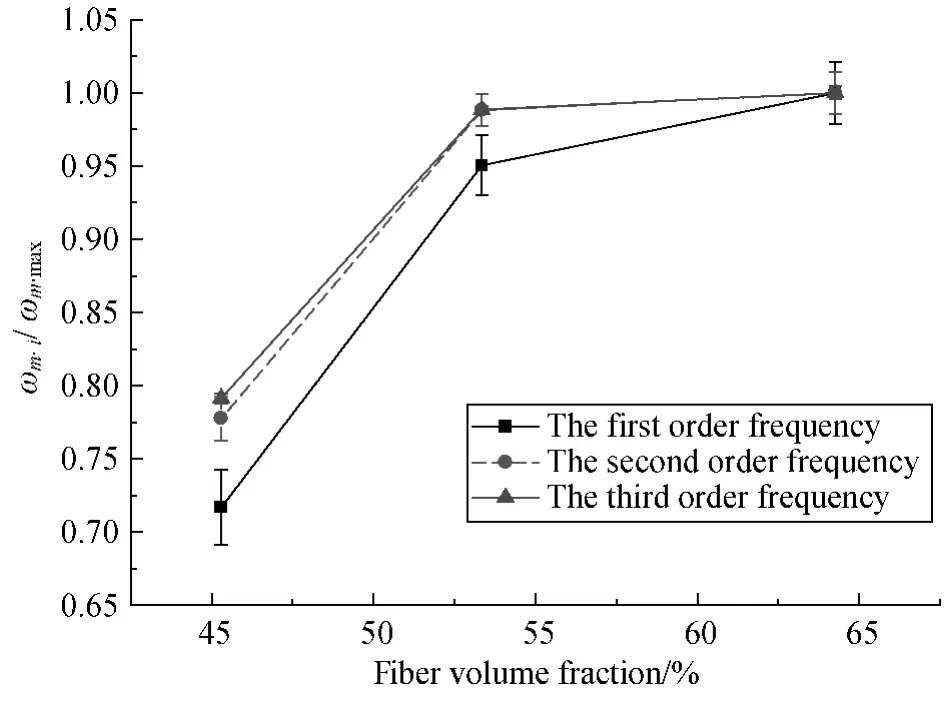
Fig.3 The relationship between fiber volume fraction and the normalized natural frequency of braided composites with braided angle A1(α1 =21°)

Figures 6-8 derive the relations between fiber volume fraction and the normalized damping ratio of first three order damping ratio of 3D-5Dir braided composites with different braiding angles(A1，A2，and A3).The curves indicate that the damping ratio dramatically decreases in each mode with the increase of fiber volume fraction.However，the decreasing degree rates have a significant variation between different modes.The third order damping ratio decreases relatively slower comparing with the first order damping ratio and the second order damping ratio.But the errors of testing results were increased significantly，which could be caused by the systematic error in high-frequency vibration.

2.3 Frequency response analyzing in frequency domain of braided composite specimens

Figures 9-11 are the amplitude responses of transfer function in frequency domain of the vibration of 3D-5Dir braided composite specimens with different fiber volume fraction and certain braiding angle (A1，A2，and A3).In these figures，the range of frequency is 0-2 000 Hz.There are three clear peaks in each response curve.The number of peaks corresponds to the excited vibration.Thus，between 0-2 000 Hz，the first three modes have been excited.Using this curve，it is possible to determine the vibrating behaviors of the beams with the first three orders.

Fig.4 The relationship between fiber volume fraction and the normalized natural frequency of braided composites with braided angle A2(α2 =33°)

Fig.5 The relationship between fiber volume fraction and the normalized natural frequency of braided composites with braided angle A3(α3 =42°)

Fig.6 The relationship between fiber volume fraction and the normalized damping ratio of braided composites with braided angle A1(α1 =21°)

Fig.7 The relationship between fiber volume fraction and the normalized damping ratio of braided composites with braided angle A2(α2 =33°)

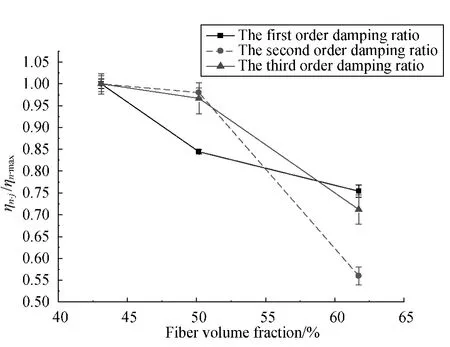
Fig.8 The relationship between fiber volume fraction and the normalized damping ratio of braided composites with braided angle A3(α3 =42°)

From these figures，it can be clearly seen that with the same braiding angle，the value of same order natural frequency increases gradually when the fiber volume fraction increases from V1 to V3，and the distance between the neighbor frequencies peaks becomes larger.The resonance of beam specimen could be difficult to excite for the higher fiber volume fraction.Moreover，for the same order natural frequency，the natural frequency amplitudes with larger fiber volume fraction are significantly higher than that with smaller fiber volume fraction.The natural frequency bandwidth becomes narrower and the peak is quite sharp，for the specimen with larger fiber volume fraction.The larger fiber volume fraction causes stronger vibration response.

2.4 Acceleration response analyzing in time domain of braided composite specimens

The amplitude responses of acceleration in time domain of 3D-5Dir braided composite specimens with certain braiding angle (A1，A2，and A3)and different fiber volume fraction are shown in Figs.12-14.From these figures，it can be seen that under the action of the impact force，the amplitude responses of acceleration are non-periodic oscillation curves and have an exponential decaying.But the oscillation levels of braided composite specimens with different fiber volume fraction are different.With the same braiding angle，the lower fiber volume fraction specimen has the smaller degree of the oscillation and the faster decaying.At the same time，the specimen (with smaller fiber volume fraction) has a smaller amplitude oscillation and a shorter time taken for oscillation disappearing.

Fig.9 Amplitude of transfer function in frequency domain of braided composite specimens with different fiber volume fraction and braiding angle A1(α1 =21°)

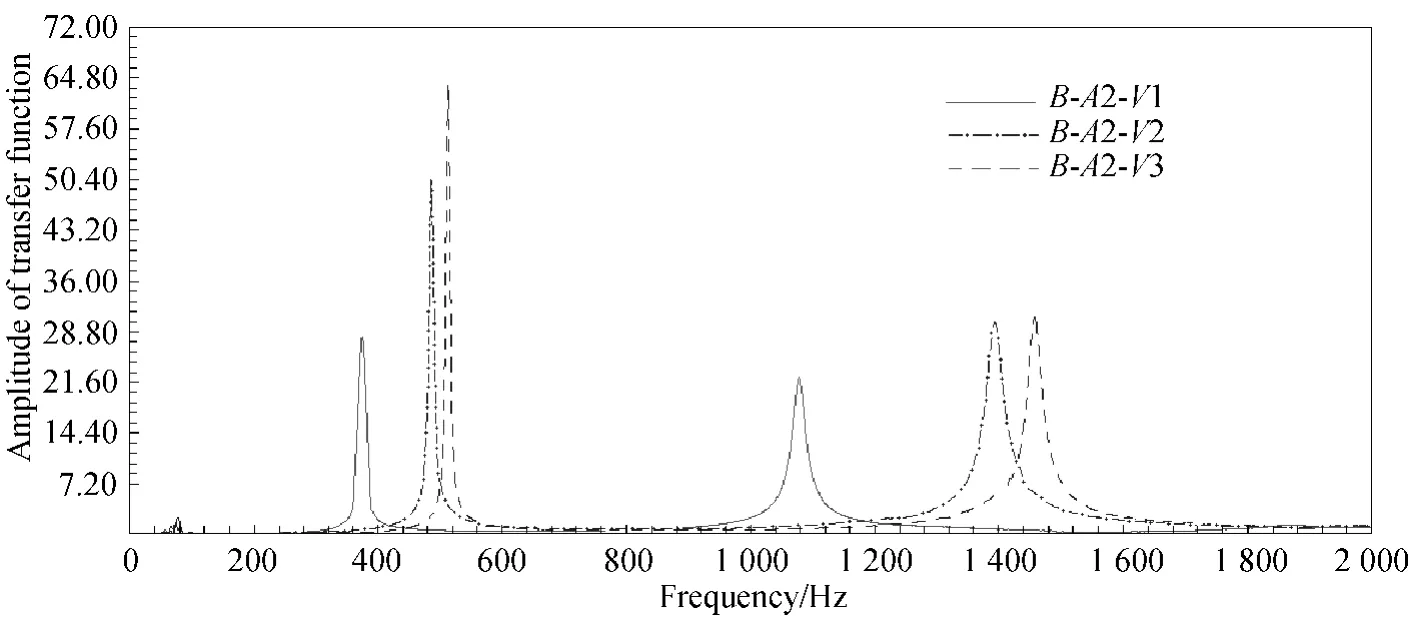
Fig.10 Amplitude of transfer function in frequency domain of braided composite specimens with different fiber volume fraction and braiding angle A2(α2 =33°)

Fig.11 Amplitude of transfer function in frequency domain of braided composite specimens with different fiber volume fraction and braiding angle A3(α3 =42°)

This means that the braided composites with smaller fiber volume fraction have better damping characteristics.These vibration characters are fairly the same with the results in Table 2.

In summary，fiber volume fraction of 3D-5Dir braided composites obviously influences its vibration performance.As the fiber volume fraction increases，natural frequency increases and damping ratio decreases.Furthermore，a larger fiber volume fraction will be valuable for the better anti-exciting property，and has an opposite effect on dissipation of vibration energy.In 3D-5Dir braided composites design，this mutual restrict relationship should be taken into consideration in order to select a suitable fiber volume fraction so that 3D-5Dir braided composites can achieve the best vibration performance and meet the need.

2.5 The comparison of the vibration properties between 3D-5Dir braided composites and laminated composites

In order to make a comparison with 3D-5Dir braided composites，the vibration testing results of laminated composite specimens with different fiber volume fraction are listed in Table 3.

Figures 15-17 are the first，second，and third order of natural frequency comparison between braided composites and laminated composites with different fiber volume fraction，respectively.

Fig.12 Amplitude response of acceleration in time domain of braided composite specimens with different fiber volume fraction and braiding angle A1(α1 =21°)

Fig.13 Amplitude response of acceleration in time domain of braided composite specimens with different fiber volume fraction and braiding angle A2(α2 =33°)

Fig.14 Amplitude response of acceleration in time domain of braided composite specimens with different fiber volume fraction and braiding angle A3(α3 =42°)

Table 3 The first three modal factors of laminated composites (average)

From these figures，it can be seen that with the increase of fiber volume fraction，the first three order frequencies of 3D-5Dir braided composites and laminated composites are increased.However when fiber volume fraction is V1 and V2，the natural frequency of laminated composites is larger than that of braided composites with braiding angle A3 and smaller than that of braided composites with braiding angle A1，and when fiber volume fraction is V3，the natural frequency of laminated composites is smallest one compared with that of braided composites.This means that with the increase of fiber volume fraction，the increase of natural frequency of braided composites is greater than that of laminated composites.When the fiber volume fraction is high，the natural frequency of braided composites is larger than that of laminated composites.When high natural frequency is needed，increasing the fiber volume fraction of 3D-5Dir braided composites is easy to achieve this purpose.

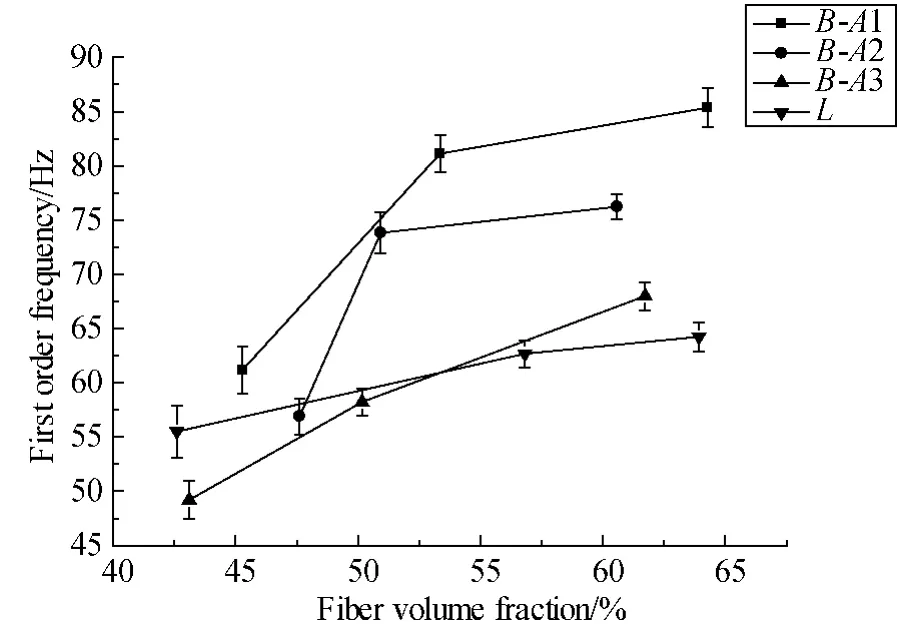
Fig.15 The first order natural frequency comparison between braided composites and laminated composites with different fiber volume fraction

Fig.16 The second order natural frequency comparison between braided composites and laminated composites with different fiber volume fraction

Figures 18-20 are the comparisons of damping ratio between braided and laminated composites with different fiber volume fraction.

Fig.17 The third order natural frequency comparison between braided composites and laminated composites with different fiber volume fraction

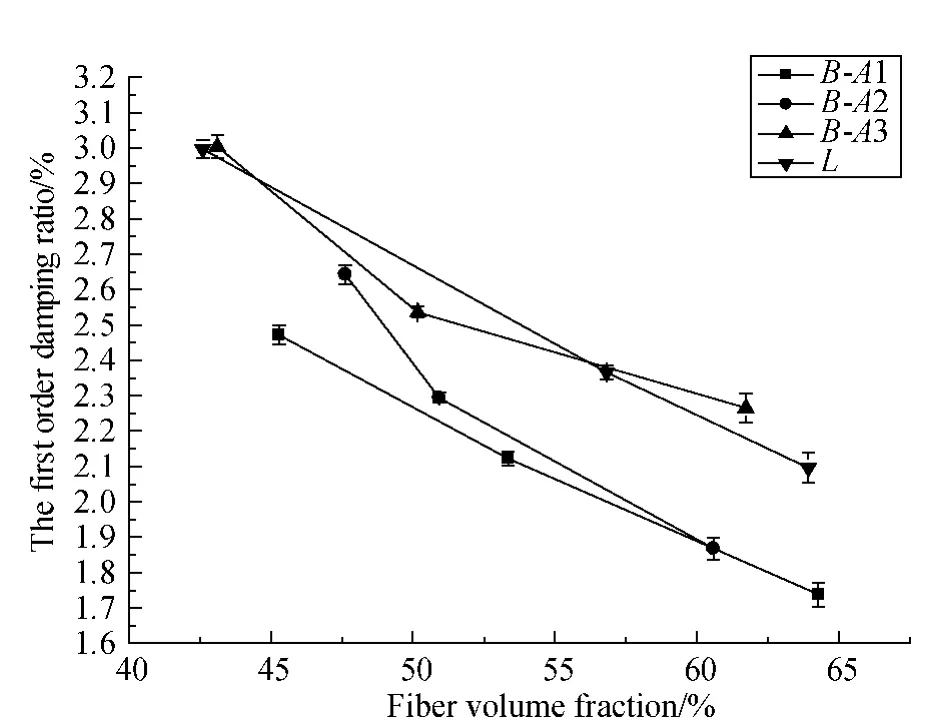
Fig.18 The first order damping ratio comparison between braided composites and laminated composites with different fiber volume fraction

Fig.19 The second order damping ratio comparison between braided composites and laminated composites with different fiber volume fraction

Fig.20 The third order damping ratio comparison between braided composites and laminated composites with different fiber volume fraction

From these figures，it can be seen that with the increase of fiber volume fraction，the first three order damping ratios of 3D-5Dir braided composites are decreased.For the laminated composites (L)，with the increasing of fiber volume fraction，the first order damping ratio is decreased，and the second，third order damping ratios are increased firstly and then decreased.For the first order damping ratio，when fiber volume fraction is V1，the damping ratio of laminated composites is almost the same with that of braided composites with braiding angle A3;when fiber volume fraction is V2 and V3，the damping ratio of laminated composites is smaller than that of braided composites with braiding angle A3 and larger than that of braided composites with braiding angle A2 and A1.For the second damping ratio，when fiber volume fraction is V1，the damping ratio of laminated composites is the smallest one comparing with that of braided composites;when fiber volume fraction is V2 and V3，the damping ratio of laminated composites is almost the same with that of braided composites with braiding angle A2，larger than that of braided composites with braiding angle A1，and smaller than that of braided composites with braiding angle A3.For the third damping ratio，for any fiber volume fraction，the damping ratio of laminated composites is the smallest one comparing with that of braided composites.This means that with the changing of fiber volume fraction，the changing range of first order damping ratio of laminated and braided composites is almost the same.However，the changing range of second and third order damping ratio of laminated composites is narrower than that of braided composites.So for the high order damping ratio，3D-5Dir braided composites are easy to meet the need through changing fiber volume fraction.

3 Conclusions

Free vibration characteristics of 3D-5Dir braided composites and laminated composites with different fiber volume fraction have been evaluated experimentally by modal analysis method subjected to a hammer excitation.The experimental results indicated that with the fiber volume fraction increase，the first three order natural frequencies had a significant increase;however the first three order damping ratios decreased relatively.For 3D-5Dir braided composites beam，the higher fiber volume fraction could reduce the resonance to be excited difficultly.And the lower fiber volume fraction obtained more energy absorption and faster energy decay.These results show the high degree of correlations between vibration behaviors and fiber volume fraction of 3D-5Dir braided composites.Comparing the vibration properties of 3D-5Dir braided composites with those of laminated composites，with the changing of fiber volume fraction，braided composites have larger changing range of natural frequency and high order damping ratio than that of laminated composites.

［1］Dion B L，Sadler R，Silverberg L.Elementary Damping Properties in Braided Composite Materials ［J］.SPIE，1994，2189:369-377.

［2］Yao X F，Yao Z H，Dai F L，et al.Experimental Modal Analysis on Dynamic Characteristics of Braided Structural Composites［J］.Acta Materiae Compositae Sinica，1998，15(4):107-112.(in Chinese)

［3］Li D S，Lu Z X，Li J L，et al.Experimental Research on the Vibration Damping Properties of 3D Braided Composites ［J］.Journal of Mechanical Strength，2009，31(2):211-214.(in Chinese)

［4］Lu Z X，Xia B，Yang Z Y.Vibration Characteristics of 3D Braided Composites Cantilever Beam ［J］.Acta Materiae Compositae Sinica，2010，27(6):172-179.(in Chinese)

［5］Cai G W，Zhou X H，Liao D X.Analyses of the Stiffness and Damping of the 4-Step Three-Dimensional Braided Composite Links［J］.Journal of Mechanical Strength，1999，21(1):18-21.(in Chinese)

［6］Cai G W，Zhong J，Liao D X.Modal Damping of Mechanisms Fabricated from Three-Dimensional Braided Composite ［J］.China Mechanical Engineering，2000，11(5):481-484.(in Chinese)

［7］Huang X L，Qiu J B.Free Vibration of Three Dimensional Braided Plates［J］.China Water Transport，2007，5(8):74-76.(in Chinese)

［8］Li Z J，Cai G W，Huang Q B，et al.Analysis of Nonlinear Vibration of a Motor-Linkage Mechanism System with Composite Links［J］.Journal of Sound and Vibration，2008，311(3/4/5):924-940.

［9］Zhang G L，Wang Y N，Li J L，et al.The Effect of Reinforcement Structure on the Modal Parameters for Sandwich Structure Composite Plate ［J］.Advanced Materials Research，2011，194/195/196:2420-2424.

［10］Gao Y，Li J L.Effects of Braiding Angle on Modal Experimental Analysis of Three-Dimensional and Five-Directional Braided Composites ［J］.Composites Part B:Engineering，2012，43(5):2423-2428.