Application of Monetary Unit Sampling Based on Extended Audit Game

ZHU Jia-jun (朱佳俊)，CHEN Ke-ming (陈克明)，ZHENG Jian-guo (郑建国)

1 School of Business，Jiangnan University，Wuxi 214122，China

2 Glorious Sun School of Business and Management，Donghua University，Shanghai 200051，China

Introduction

Audit sampling is the application of audit procedures to less than 100% of items within a population of audit relevance such that all sampling units have a chance of selection in order to provide the auditor with a reasonable basis to draw conclusions about the entire population［1］.In other words，the standard recognizes that auditors will not ordinarily test all the information available because this would be impractical as well as uneconomical.Instead，the auditors will use sampling as an audit technique in order to form their conclusions.However，so long as sampling techniques are employed in the auditing process，there will be sampling risk，which will affect auditing risk levels through evaluation of material misstatement risks and the determination of detection risks.Therefore，sampling risk and audit efficiency have always been hot research topics in modern auditing.

The sampling techniques classically used in auditing are divided into two categories:attribute sampling and variables sampling.Monetary unit sampling (MUS)， also called probability-proportional-to-size or dollar-unit sampling，is one of the most important methods in audit sampling for determining the accuracy of financial accounts.Based on combining attribute sampling with variables sampling， MUS can express a conclusion in dollar amounts rather than as a rate of occurrence.It is commonly used by auditors to test accounts such as accounts receivable，loans receivable，investment securities，and inventory［2］.Although MUS has a strong advantage in audit sampling and analysis，there are still some deficiencies:firstly，the audit risks and coefficients cannot really reflect the relationship between the audit costs and benefits，audit risk and sampling，which are assumed by the auditors;secondly，the Poisson distribution can be used to estimate risk factors of different misstatements，but cannot accurately measure the effects of expected error on risk factors［3］;thirdly，common MUS estimation practice does not explicitly recognize the multiple distributions within the population of account errors，which often leads to excessive conservatism in auditors'judgment of population error;fourthly，due to the limitations of static errors and conservative estimate policies，audit policies can not reflect the dynamic error range of audit policies［4］.To a certain extent，the sampling precision and error analysis are affected as a result of policies assessment.

The control of audit risks and sampling errors is always remarkable.After years of development， a number of evaluation techniques have been used to improve the traditional MUS，in order to control the Type II error (the risk of incorrect acceptance) and the Type I error (the risk of incorrect rejection)，for example，the modified moment bound(MM)，the Clayton's combined bound (CL)［5］，the multinomial-Dirichlet bound (MD)［6］，the Stringer bound(ST)［7］，the Bayesian normal bound(BN)［8］，etc.In the sampling error analysis of MUS，Higgins and Nandram［9］used the Zero-Inflation Poisson (ZIP)distribution to consider zero versus nonzero errors and to handle the real populations of account errors.An algorithm yielding the optimal solution in time and space linear to the number of population units is given by Carrizosa［10］when units sizes have very large variability.An extended multinomial-Dirichlet model for error bounds for dollar-unit sampling was established by Swinamer et al.［11］，which is reliable and efficient for most of the real populations studied.

There is no doubt that the accuracy and the reliability of audit sampling are the basis of audit judgment.On account of the problem of incomplete information in strategy selection of audit game，this article uses a strategic auditing approach to improve error analysis and interval estimation techniques of MUS centers on audit risk in order to study expected return and strategy matrix，irregular tendency and benefits transfer of the auditee under hidden action.Costs and benefits of extended audit game under respective conditions were analyzed in order to measure the incidence of Type I and Type IIerrors and the precision of audit sampling.Not only does this method take the advantages of MUS in auditing，but also obtains the relation between audit risk with audit sampling，conducive to the promotion of the judgment results of multi-factor analysis and multi-stage evaluation in extended audit game.

1 Audit Strategy and Risk Based on Mixed Game

Game theory is a subject appeared in early 20th Century，which is widely applied in behaviors and tactics analysis.The game-theoretic strategic auditing approach， pioneered by Fellingham and Newman［12］，identifies the strategic component of auditing as critical in detection and deterrence of management fraud.The method is used to simulate the interaction between auditors and audited firms［13-14］.This allows a more detailed investigation of the way that auditors' and auditees' actions are affected by the actions or threat of actions of the other party.

1.1 Major assumptions of audit game

Auditing is a monitoring device that acts as a mechanism to detect and deter material irregularities.However，the auditing environment is interactive.The major assumptions of audit game model are as follows:

(1)the auditor and the auditee are utility maximizers;

(2)the precision of the audit efficiency and effectiveness is known to the auditor and the auditee;

(3) the payoffs associated with the outcomes are exogenously specified;

(4)the payoffs and preferences of the auditor and auditee are common knowledge.

In audit game， there are two choices (“no major irregularities”and“significant violations”)which can be made by the auditee.The choice of“no major irregularities”indicates compliance with accounting regulations and guidelines，while in the selection of “major violations”， i.e.， violation of accounting regulations and guidelines， the auditee always claimed that the statements and accounts were provided compliance with regulations.Therefore，this game reflects not the constant sum，but variable sum game based on local conflicts and incomplete information，so its essence is a strategy analysis model for hiding the behavior and incomplete information.

1.2 The mixed strategies and Nash equilibrium of audit game

Definition 1 Assume that Z={V1，V2，…，Vn;u1，u2，…，un}is a standard-game participation by n-person，Vi= {Vi1，Vi2，…，Viγ}is the strategy space of participant i，“mixed strategy”means “strategy”which is randomly selected by participant i in its alternative strategy γ according to the probability distribution Pi={Pi1，Pi2，…，Piγ}，0≤Pij≤1，∑Pij=1，j =1，2，…，γ.

Definition 2 Assume that V and T are strategy sets of the two sides of audit game，mixed strategy sets are X and Y，and benefit matrices are KAand KR.(x，y)can be called a mixed strategy Nash equilibrium if mixed strategy (x，y)∈X × Y satisfies the following conditions:

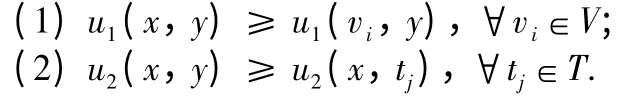
where，∑xi= 1，∑yj= 1.

Definition 3 Assume that α is the probability of auditor accepting the account balance，β is the probability of auditee choosing“no material irregularity”.A game strategy matrix (Table 1)can be obtained after combining the choice behaviors of auditor and auditee.Assuming that B is the return of the auditor and L is the return of the auditee，A =(α，1-α)and O=(β，1-β)are the strategy probabilities of auditor and auditee.Then，a mixed strategy Nash equilibrium is established.0≤α≤1，0≤β≤1，0≤B1＜B2＜B3＜B4，0≤L1＜L2＜L3＜L4［15］.

Table 1 Mixed strategies matrix of audit game

According to the return of the auditor and auditee，the Nash equilibrium theory can be employed to arrive at Eqs.(3)and (4)，respectively for the probability of acceptance by the auditor and the probability that the auditee commits no material irregularity.Substituting α and β into the strategies of the auditor and auditee respectively，Eqs.(1)and (2)can be arrived at.Among them，δ ＞0 stands for the profit differences between the auditor's overall strategies of acceptance and rejection;φ ＞0 refers to the profit spread between the auditee's overall strategies of material irregularity and no material irregularity;θ ＞0 represents the product of the differences between the aggregate profits of the auditor and auditee.

1.3 Risk analysis of mixed audit game

Corollary 1 Based on the mixed strategy Nash equilibrium，a game probability matrix between the auditor and the auditee can be obtained:

According to the mixed strategy Nash equilibrium，there are four possible outcomes of the audit game probability matrix:{no material irregularity，accept}，{no material irregularity，reject}，{material irregularity，accept}，{material irregularity，reject}，in which {no material irregularity，reject }constitutes the risk of incorrect rejection and {material irregularity，accept}constitutes the risk of incorrect acceptance.

Corollary 2 Based on the mixed strategy Nash equilibrium，the risk of incorrect acceptance can be expressed by S and the risk of incorrect rejection can be expressed by R，0 ＜ R ＜1，0 ＜S ＜1.Then，the formulas of S and R are:

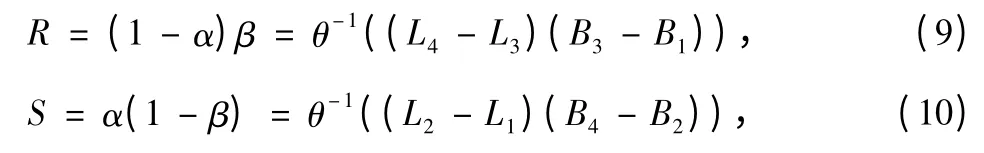
Corollary 3 Based on the mixed strategy Nash equilibrium，when α=β，there must be an equality between Type I and Type II errors，namely，R = S;that is，when R = S，(L4-L3)(B3-B1)=(L2-L1)(B4-B2).

So when (L4- L3)(B3- B1)＞(L2- L1)(B4- B2)，Type I error is greater than Type II error，R ＞S;when (L4-L3)(B3-B1)≤(L2-L1)(B4-B2)，Type I error is less than Type II error，R≤S.

2 The Extended Audit Game Based on Incomplete Information

The extended audit judgment process has been added into traditional audit game in order to increase strategic advantage for auditors and help further analysis of the relation between audit costs and audit risk.

2.1 Mixed strategy and cost analysis of extended audit game

For the purposes of this stylized model，the auditing process is divided into two phases:the primary audit and the extended audit.The auditor may make an accept/reject decision after the primary audit or after the extension of audit procedures.At this time，the auditee has only two strategies，but the auditor has three strategies，so a new audit game model under incomplete information is constituted.

Definition 4 Assume that αcand zcare the probability of acceptance and rejection by the auditor respectively，hcis the extended audit probability，αc+zc+hc=1，wcis the acceptable probability of extended audit，1 -wcis the rejected probability of the extended audit，and βcrepresents the probability of auditee choosing“no material irregularity”.Let 0≤B1＜B2＜B3＜B4be the initial return of auditor and 0≤L1＜L2＜L3＜L4be the initial return of auditee.When extended audit occurs，C is the additional cost of the auditor，but auditee does not need to spend an additional cost.Auditors and audit actions constitute an extended game strategy matrix (Table 2)，among which，Ac= (μc，νc)is the auditor's strategies and Oc= (βc，1 -βc)is the auditee's strategies，μc= αc+ hcwc，νc= zc+ hc(1 -wc)，c = 1，2，3，…，which is used to represent a policy variable of extended audit.Thus，a mixed strategy Nash equilibrium is established.

Table 2 Mixed strategies matrix of extended audit game

Equation (11)for the probability of acceptance by the auditor αcand Eq.(12)for that of rejection by the auditor zccan be arrived by the probability of expanded auditing hcand the probability of expanded acceptance wc，from which the formula β for the probability that no material irregularity is committed on the part of the auditee after expanded auditing is derived as follows:

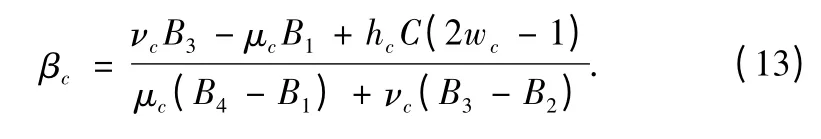
When the extended audit occurs，the return of the auditee is unchanged，and the auditor needs to spend the cost of C，so that it will affect the game strategy changes between auditee and auditor.In particular，when the extended audit and extended audit cost are not considered，that is，h=0 and C =0，αc=φ-1(L2-L1)，βc=δ-1(B3-B1)，zc=1 -αc，then Definition 3 is a special form of Definition 4.

2.2 Risk analysis of extended audit game

Corollary 4 Based on the mixed strategy Nash equilibrium，an extended audit game probability matrix between the auditor and the auditee can be obtained:

Corollary 5 Based on the mixed extended strategy Nash equilibrium，the risk of incorrect acceptance can be expressed by Scand the risk of incorrect rejection can be expressed by Rc，0 ＜Rc＜1，0 ＜Sc＜1.Then，the formulas of Scand Rcare:

Corollary 6 Based on the extended audit game，when αc+hc·wc= βc，there must be an equality between Type I and Type II errors，that is，Rc=Sc.

When Rc=Sc，hc≠0 and w≠0.5，extended audit cost can be obtained:where σ=μB4-νB2，τ=νB3-μB1，because C ＞0，so (L2-L1)σ ＞(L4-L3)τ.

Different extended audit probability wchas different effects on the extended audit cost C and plays a different role.The extended audit cost C includes not only the material and cost of additional spending，but also the time and energy consumed.Compared with the ordinary audit game theory，the more the expanded auditing cost C is paid by the auditor during the auditing process，the smaller the Type I risk，the bigger the Type II risk.Reasonable expanded auditing costs can be employed to analyze the relationship between auditing costs and efficiency，which helps auditors adjust auditing strategies and sampling scales.

3 Improvement of MUS Based on Extended Audit Game

By introducing the extended audit game，the dynamic，quantitative audit risk strategy can be integrated into the sampling process，a systematic risk analysis tool for audit sampling，in order to expand the range of applications of audit sampling.

3.1 Sampling risk and sample size

Definition 5 Assume that the acceptable level of Scis the risk of incorrect acceptance，the number of Scobeys a Poisson distribution，λ is the reliability factor，and ε is the number of misstatements for the sampling application.

Let n be the sample size，p the probability of an individual monetary unit being misstated，λ=n×p，BVthe recorded book value for the population total，TMthe tolerable misstatement based on planning materiality，EMthe expected amount of misstatement in the population，and Scthe acceptable level for the risk of incorrect acceptance.Then the probability p is given by p = TM/，so that λ = n·TM/BV.As the number of errors runs up to ε the auditor will accept the sampling result.When no errors are to be accepted，from Eq.(19)，we get Sc= exp(- np)，from which

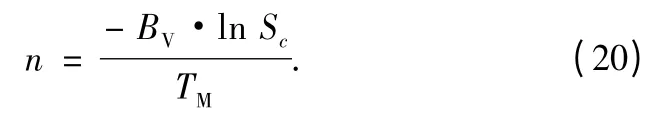
According to the characteristics of the Poisson distribution，the distribution of n samples can be obtained with the range of p(Table 3).

The sample size may not equal the number of items actually tested.Here n actually equals the number of intervals selected.Amounts over the interval might actually consist of one or more intervals from the n.According to Eq.(20)，Sampling Interval(SI)can be calculated as

Table 3 Sample size estimation based on p

3.2 Expected misstatement and reliable function

Based on the Nash equilibrium of mixed expansion strategy，each misstatement ε corresponds to a single the EMin error analysis.EM(perhaps based on the experience of prior years)represents the auditor's best estimate of the population misstatement.

The (conservative)assumption made in audit sampling is that all misstatements are 100% misstatements.Thus m/n=EM/BVor，equivalently

If all misstatements are 100% misstatements，H is the expected error rate which can be calculated with Eqs.(20)and (23)(Table 4)in order to help auditors to consider the impact of Scon H and select the optimal sampling strategy.

Table 4 H based on Sc

By the table lookup method，the approximate reliability factor λ should be calculated.But not all confidence coefficient and data flow among the misstatements are shown in traditional table lookup method.The approximate interpolation method can construct confidence function in accordance with the existing H and λ in order to obtain reliability factor λ according to arbitrary EM.

Definition 6 Suppose Pkis a set of k-order polynomials，H0，H1，…，Hkis a group of different interpolation nodes of the expected error，λi=f (Hi)is k order polynomial interpolation，the interpolation polynomial Pk(H)∈P of the reliability factor can satisfy the following conditions:

where Pk(H)is called reliability factor of the interpolation polynomial，f(H)is a function of the reliability factor and［min(Hi)，max(Hi)］is the interpolation interval of reliability factor，r(H)is the interpolation remainder term，and (Hi，ζi)is called data points.

Definition 7 Suppose that the k-order polynomial Pk(H)to meet the Definition 6，

where Pk(H)is called the Lagrange interpolation formula，and lt(H)is called interpolation basis function.

Corollary 7 If confidence level Pkis a k-order polynomial and Pk(H)is the k-order Lagrange interpolation polynomial of f(H)，then Pk(H)≡f(H).

Based on the interpolation polynomial Pk(H)of expected error，it's easy to obtain reliability factor λ to achieve integrating Type II error and statistical sampling.

3.3 Sampling interval analysis

Upper Error Limit (U)is the maximum possible error estimated in the population as a result of the substantive test of samples.If the U is above the materiality limit，then the auditor will either perform further substantive tests to check whether there is a material error or conclude that there is a material error.

U consists of Most Likely Error (ML)with allowance for sampling risk (AR)，then U may be determined by

where ML= ∑MLiis an estimation of the error in the population.If recorded value (BVi)is less than sampling interval，then MLiwill be estimated based on net tainting percentage(Tpi)and sampling interval;if BViis greater than or equal to the sampling interval， then MLiis the actual misstatement between BViand audited value (AVi).After carrying out substantive test of details，the MLwill be projected based on actual sample results and used for drawing audit conclusions.

Note that MLis the point estimate，which is the equivalent of sample mean and U equals the confidence bound.ARconsists of basic precision (BP)with the incremental allowance (IA).

where BPis the allowance for errors which exist but no evidence of that is found in the sample.It is dependent on the confidence level and the size of the sample and is present even where no errors have been found in the sample.If no differences are discovered， then the BPfor both overstatements and understatements may be determined by

IAis used to describe the uncertainty of sampling results，this allowance is the difference between the expected error rate and the tolerable deviation rate.Multiply the ranked MLiwhich BViis less than SIfrom highest to lowest by λiand sum the products，then IAmay be determined by

Especially，if no misstatements in sample are found，IA= 0.

Definition 8 Suppose that b overstatements and d understatements are found， and that reliability factors of overstatement differences are λ1，λ2，…，λb，reliability factors of understatement differences are λ1，λ2，…，λd.Suppose further that the ratios of overstatement differences to their respective recorded book values，sorted in descending order，are G1，G2，…，Gb，similarly，the tainting of understatements is Q1，Q2， …， Qd.Then the U for overstatements and understatements are given by

If every recorded value is less than sampling interval，then Eqs.(34)and (35)are changed into:

Corollary 8 If the following conditions are met，then |UO| =|UU|.

(1)If every recorded value is less than sampling interval;

(2)b = d;

Proof If |UO| = |UU|and every recorded value is less than sampling interval，then UO= -UU，

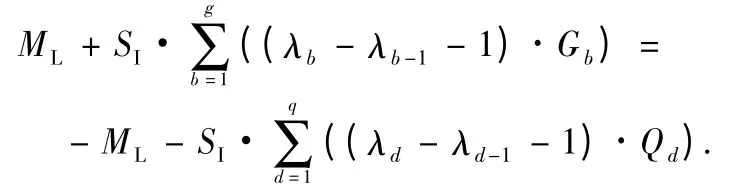
After substituting MLwith Eq.(38)，

After substituting b = d and there must be SI≠0 in audit sampling，

Thus，if D ＞0，then |UO| ＞|UU|;if D ＜0，then |UO| ＜|UU|.Specially，when b = d，D is used to help auditors determine the relationship between the error rate and the number of errors and analyze the impact of sampling error on the sample size and the direction of the errors.

If (UU，UO)∈(- TM，TM)，it is concluded that population is not misstated by more than TMat the specified level of sampling risk，so the result can be accepted，otherwise the sampling interval liable to be rejected.U is the dynamic region due to the dynamic values.Therefore，it can be used to observe the impact of audit risk on the population valuation range，and calculate the valuation range when audit game equilibrium.

4 Simulation

Suppose，for example，that an auditor is auditing a population (2 535 items)with a recorded book value of$2 580 700 with a tolerable misstatement of $100 000，and B1=$ 10000，B3= $ 20 000，B4- B2= $ 15 000，C =$5 000.Because auditors do not have the true figures so they will have to make some approximations about the auditee's income between “major irregularities” and “no major irregularities”，so suppose L4-L3=$72 000，L2-L1=$66 000.

According to Eqs.(15)-(16)，Type I error Rcand Type II error Sccan be calculated when hc= wc，and the values range of Scfrom 5.6% to 21.7% (Fig.1)，so the values range of confidence from 89% to 57%.When no more errors are discovered，the sample size n also can be calculated by Eq.(20)，n increased with the increasing probability in which auditor accepts the account balance(Fig.2)，at the same time，max(n)= 268 if Scis smallest and min(n)= 200 if Scis greatest.

Fig.1 The trends of Sc

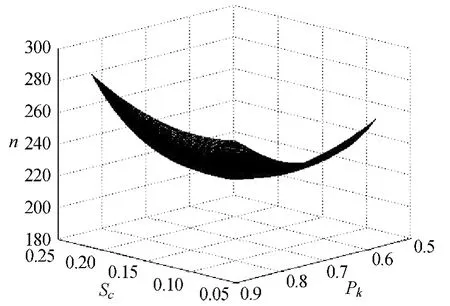
Fig.2 The trends of n under Sc and Pk

Based on the sample of n，the audited values for recorded amounts of $1 800，$680，$920，$1 280，and $1 160 are $ 1 080，$ 950，$ 1 220，$ 980，and $ 860，respectively (Table 5).There are three overstatements and two understatements.Arrange the rate of tainting in descending order for overstatement and understatement separately.

Table 5 Number of audit errors

Due to all the recorded values are less than sampling intervals，therefore，Eqs.(29)and (30)can be used to calculate ML，which is an important point estimate method of MUS for error analysis.When the condition is min(Sc)，the UOfor overstatements is given by Eq.(36)as$34 729.2，and the UUfor understatements is therefore given by Eq.(37)as $-30 613.2(Table 6).As the U is less than the materiality limit the auditors can conclude that there is no material error and the sampling results could be acceptable to auditors under 89%confidence.If the U is more than the materiality，then the auditors will reject the sampling results，and conclude that there is a material misstatement in the accounts.

Table 6 Analysis of audit risk and sampling error

Similarly，under the conditions of max (Sc)，U can be calculated also which meets the requirements of the sampling error under 57% confidence.Through two kinds of error analysis under equilibrium conditions，auditors can consider that audit risk has had a big influence on the sample size and errors.In particular， zero or negative balances must be tested separately.

From the point of view of Sc，Pkand UOmove in the opposite direction of Sc，and UUincreases with decreasing Pkand increasing Sc，and the lower the Pk，the greater the Sc.Affected by the degree of overstatements and understatements，the rate at which UUdecreases is greater than that at which UOincreases(Figs.3-4).

Under the same Pk，the confidence intervals of each sampling method include the book value，which supports the conclusion that the account is not materially misstated (Table 7).But the precision intervals of the new MUS method based on the extended audit game are more effective than the Mean Per Unit (MPU)method.In addition，as a static sampling approach，MPU method can only calculate the confidence interval under prescribed confidence level，and it does not reflect the procedure of audit strategy judgment and selection.

Fig.3 The trends of UO under Sc and Pk

Fig.4 The trends of UU under Sc and Pk

Table 7 Comparison of confidence interval between new MPU and MUS

5 Conclusions

The traditional audit sampling can only achieve static sampling analysis and internal estimation by the subjective judgment of the audit risk.In addition，traditional audit sampling methods for Type I error and Type II error in audit risk systems require too many ideal conditions.An objective and high precision parameter estimation is very important to the audit sampling system design and improvement.Through analysis of game strategy and audit risk between auditor and auditee，variable sampling can not only achieve quantitative and dynamic estimates of audit population，but also obtain numerical characteristics of population and form systematic judgment about misstatement.As a result，it improves the accuracy and the reliability of analyzing receivables，inventories，wage costs，trading activities，etc.，in audit sampling.

The model's main role is as follows.Firstly，the method introduces audit sampling into the theories and techniques of audit game.Risk analysis and statistical sampling are combined to realize comparison and selection of game strategies with incomplete information and hidden action in order to improve the audit sampling methods.Secondly，it is used to research the relation between expected error and the number of misstatements based on the reliability factor function and Lagrange interpolation formula in order to meet the needs of discrete and continuous interpolation and expand the scope of the application of confidence level.Thirdly，based on the extended audit game，the variation and balanced conditions of risk of incorrect rejection and risk of incorrect acceptance can be observed，and the formulas of overall misstatements level are established to achieve sample selection and error estimation under dynamic game.Fourthly，through the cost and probability of extended audit，the effect and variation of statistical sampling can be observed and the relationship among the audit cost，and audit strategy change and statistical inference can be analyzed.

The financial statements consist of the income statements，balance sheet，and statement of cash flows.These financial statements may be inaccurate and auditors may need to find additional information to make sure that the information provided by these financial statements is reliable.The extended audit sampling model which combines audit game and statistical sampling.It is used to help the auditor determine which auditing procedures for accounts or transactions in the financial statements can help decrease the audit risk to an appropriate level.Auditors can decide the requirements of extended audit through the audit situation，and statistical data and priori probability are combined to determine reasonable extended audit probability and audit costs，to control audit risk and cost.Audit strategy and confidence level under incomplete information，thus improving the accuracy and the reliability of audit sampling error analysis.

［1］Power M K.From Common Sense to Expertise:Reflections on the Prehistory of Audit Sampling［J］.Accounting，Organizations and Society，1992，17(1):37-62.

［2］Carpenter B，Dirsmith M.Sampling and the Abstraction of Knowledge in the Auditing Profession:an Extended Institutional Theory Perspective［J］.Accounting，Organizations and Society，1993，18(1):41-63.

［3］Span G A，Popa I E.Mathematical Optimum of the Audit Sample［J］.American Journal of Applied Sciences，2012，9(8):1290-1293.

［4］Jr Messier W F，Kachelmeier S J，Jensen K L.An Experimental Assessment of Recent Professional Development in Nonstatistical Audit Sampling Guidance［J］.Auditing:A Journal of Practice ＆Theory，2001，20(1):81-96.

［5］Clayton H R.A Combined Bound for Errors in Auditing Based on Hoeffding's Inequality and the Bootstrap［J］.Journal of Business＆Economic Statistics，1994，12(4):437-448.

［6］Tsui K W，Matsumura E M，Tsui K L.Multinomial-Dirichlet Bounds for Dollar-Unit Sampling in Auditing［J］.The Accounting Review，1985，60(1):76-96.

［7］Bickel P J.Inference and Auditing:The Stringer Bound［J］.International Statistical Review，1992，60(2):197-209.

［8］Dworin L，Grimlund R A.Dollar-Unit Sampling:a Comparison of the Quasi-Bayesian and Moment Bounds［J］.The Accounting Review，1986，61(1):36-57.

［9］Higgins H N，Nandram B.Monetary Unit Sampling:Improving Estimation of the Total Audit Error［J］.Advances in Accounting，2009，25(2):174-182.

［10］Carrizosa E.On Approximate Monetary Unit Sampling［J］.European Journal of Operational Research，2012，217(2):479-482.

［11］Swinamer K，Lesperance M，Will H.Optimal Bounds Used in Dollar-Unit Sampling:a Comparison of Reliability and Efficiency［J］.Communications in Statistics—Simulation and Computation，2004，33(1):109-143.

［12］Fellingham J C，Newman D P.Strategic Considerations in Auditing［J］.The Accounting Review，1985，60(4):634-650.

［13］Cook J，Hatherly D，Nadeau L，et al.Does Cooperation in Auditing Matter?A Comparison of a Non-cooperative and a Cooperative Game Model of Auditing［J］.European Journal of Operational Research，1997，103:470-482.

［14］Chou P B，Xu W，Anandarajan A，et al.Is Honesty the Best Policy? A Game Theory Perspective of Auditing ［J］.International Journal of Behavioural Accounting and Finance，2012，3(1/2):88-106.

［15］Deshmukh A.The Role of Audit Technology and Extension of Audit Procedures in Strategic Auditing［J］.International Journal of Applied Quality Management，1999，2(2):187-209.

［16］Gillett P R.Monetary Unit Sampling:a Belief-Function Implementation for Audit and Accounting Applications［J］.International Journal of Approximate Reasoning，2000，25(1):43-70.