云南石门坎水电站坝基岩体变形模量与波速相关关系研究

李 雷，闫思泉

（黄河勘测规划设计有限公司，河南郑州450003）

云南石门坎水电站坝基岩体变形模量与波速相关关系研究

李 雷，闫思泉

（黄河勘测规划设计有限公司，河南郑州450003）

水利水电工程勘察过程中，根据岩体变形模量与波速相关关系，测试岩体波速，便可大范围确定岩体变形模量。通过对多项工程岩体变形模量与波速关系统计分析可知，变形模量与波速的关系为非线性，指数函数形式较为合适。本文利用5种指数函数形式，对云南石门坎水电站坝基岩体变形模量与波速进行拟合分析，以决定系数、残差平方和与自由度的商作为标准，评价拟合效果。结果表明，岩体变形模量与波速关系1阶递增指数函数为最优。

变形模量；波速；相关系数

1 引言

岩体在荷载作用下产生变形，如果荷载不断增加，变形也不断增加，最后导致岩体破坏；或荷载达到某一值后，保持恒定，变形持续增长，最后也能促使岩体破裂。因此岩体变形模量成为水利水电工程勘察设计中非常重要的力学参数。

岩体变形模量取决于岩块、结构面及充填物的性质，在水利水电工程勘察设计过程中，岩体变形模量通常采用承压板法试验获得，该试验试件加工复杂、周期长、耗资大，得到的数据只是局部的。近些年来，使用钻孔弹模法较多。该方法虽然较承压板法轻便灵活，但是依旧不宜展开大范围测试。

岩体声波速度的大小主要取决于岩性、结构面的性质和数量、以及它们之间的组合关系，因而不仅能反映岩体的地质因素，同时在一定程度上也可以表征岩体的变形特征，反映岩体的力学属性。岩体声波波速测试，方法简单、快捷、费时少，对岩体没有破坏作用。

由于岩体结构的复杂性和岩体性状分布的不均匀性，现场大型岩体变形试验只能取得有限点的资料，不能完全反映工程区岩体变形参数。而声波测试可以掌握大范围岩体的完整性和岩体质量的优劣。在现场做好工程地质分区，利用声波测试取得定量指标，通过建立波速与岩体变量模量的相关关系，便可进行大范围岩体变形参数的评价。

2 变形模量与波速相关关系类型分析

岩体变形模量与声波波速之间的相关关系，曾有多种不同类型的拟合函数形式。Barton等［1］根据建立的岩体纵波速度Vp与Q值（Q为1974年挪威的Barton等人提出的岩体质量指标，下同）的关系以及Q值与岩体变形模量的关系，推导出了岩体纵波速度与岩体变形模量的关系：

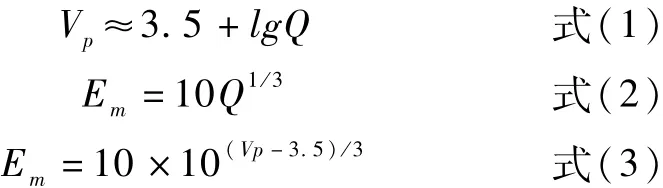
我国学者对岩体波速与变形模量之间的关系进行研究，文献［2］将Barton早期建立的岩体变形模量与Q值的关系Em=25lgQ和式（1）结合起来推导，得到岩体变形模量与波速之间的关系，即：

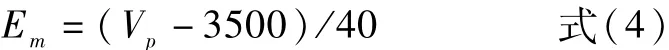
该研究同时利用岩石力学参数管理系统ROMEDA中丰富的数据经拟合认为，式（4）过高地估计了岩体变形模量，建议采用Em=（Vp-3500）/80进行估算。同时给出了花岗岩纵波波速与岩体变形的关系为：

冯国栋等［3］根据姚河坝岩体变形模量和纵波波速的实测数据，拟合了如下的关系：

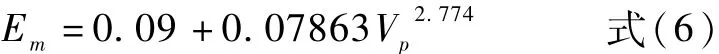
从文献［4］统计的国内12个水电工程岩体动静对比关系可以看出，有6个工程岩体变形模量与波速相关关系型式为指数函数，5个工程为幂函数，岩体变形参数与波速关系中函数类型不统一、参与统计的数量不统一、相关系数不统一。根据国内20多个大中型水电工程589对数组统计结果，得出如下几个特点：①数组分布为非线性，均符合指数函数和幂函数规律，但指数函数更接近点群；②低波速段变形模量离散性较小，高波速段变形模量离散性较大；③指数函数和幂函数的相关关系均大于0.70；④部分数组偏离关系曲线较远。三峡水利枢纽坝基岩体变形模量与波速关系为指数函数Em=0.0123e1.4277Vp［5］。乌江构皮滩水电站坝基岩体变形模量与波速关系为指数函数，Em= 0.69e0.7244Vp［6］。对云南省小湾水电站坝基岩体进行了72组动静对比测试，利用其中42组代表性数据拟合分析，变形模量与波速相关关系为指数函数Em=0.012586e0.001438Vp［7］。

由三峡水利枢纽工程坝基岩体、乌江构皮滩水电站［4］、巴基斯坦高摩赞枢纽工程［8］等工程岩体变形模量及声波波速测试资料可知，某一特定工程变形模量值主要集中在某一波速区段，高波速段和低波速段较少。

综上所述，岩体变形模量与波速的关系形式有直线函数（Em=aVp+b）、幂函数（Em=aVbp、Em= R+aVbp）、指数函数（Em=a10Vp+b、Em=aebVp）。经过对比，结合实际工程资料分析，认为岩体变形模量与波速的关系为非线性，指数函数形式较为合适。

3 变形模量与波速相关关系研究

对岩体变形模量与波速相关关系采用非线性模型—指数函数进行分析。对于非线性模型，设有n组观测数据i=1，2，3，…，n。设因变量Yi和自变量Xi满足：

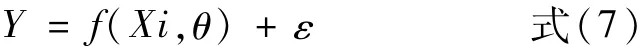
经过拟合，求出最佳参数θ。非线性拟合的结果利用决定系数和残差平方和来评价。①决定系数：在Y的总平方和中，由X引起的平方和所占的比例，即相关系数的平方，记为R2（R的平方）。决定系数的大小决定了相关的密切程度。当R2越接近1时，表示相关的方程式参考价值越高；相反，越接近0时，表示参考价值越低。对于同一组数据，越大越好。②残差平方和χ2：每一点Y的估计值与实际值之差的平方之和称为残差平方和。即：

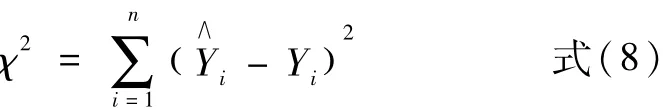
对于同一组数据来说，残差平方和越小，其拟合程度就越好。采用多参数函数型式拟合，有：

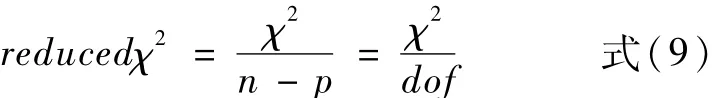
式中：n—参与拟合的数据点数目，p—参数的数目，（n-p）—自由度（degreesoffreedom）。对于同一组数据，其reducedχ2值越小越好。

4 工程应用研究

云南石门坎水电站拱坝坝基岩体有3种岩性，第1种为灰白色石英砂岩，第2种为青灰色钙质细砂岩，第3种为紫红色泥钙质粉砂岩。根据坝基开挖后现场钻孔弹模试验及声波测试成果，对坝基不同岩性岩体的变形模量和声波波速资料，通过归类分析，舍去不合理的离散值，按照下列5种指数函数形式进行非线性拟合。式（10）为最简单指数形式，式（11）为常用指数形式，式（12）～（14）分别为1阶递增指数函数、2阶递增指数函数、3阶递增指数函数。

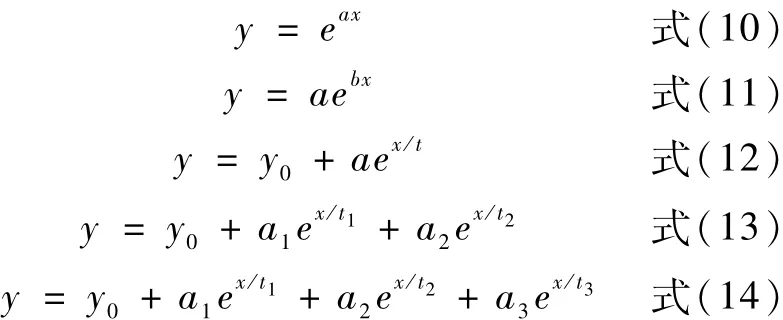
为便于分析对比，式（10）～（14）分别编号为A、B、C、D、E5种类型。将这5种函数拟合结果评价参数列于表1中。从表1分析可知，石英砂岩5种指数形式拟合的决定系数R2是由小变大，reducedχ2由大到小；从这2个指标评价及其相关关系分析可知，5种指数形式由简单到复杂，其拟合结果越来越好。钙质细砂岩变形模量与波速关系函数，reducedχ2值由大到小再到大，决定系数R2由小到大再到小；第3种指数函数最优。泥钙质粉砂岩变形模量与波速关系函数，reducedχ2值由大到小再到大，决定系数R2由小到大再到小；第3种指数函数最优。上述5种指数函数形式是由简单到复杂。式（10）最简单，只有1个参数。式（13）有5个参数，式（14）有7个参数。参数越多，需要的试验数据也就越多，相应地，试验组数增加，费用代价也越高。

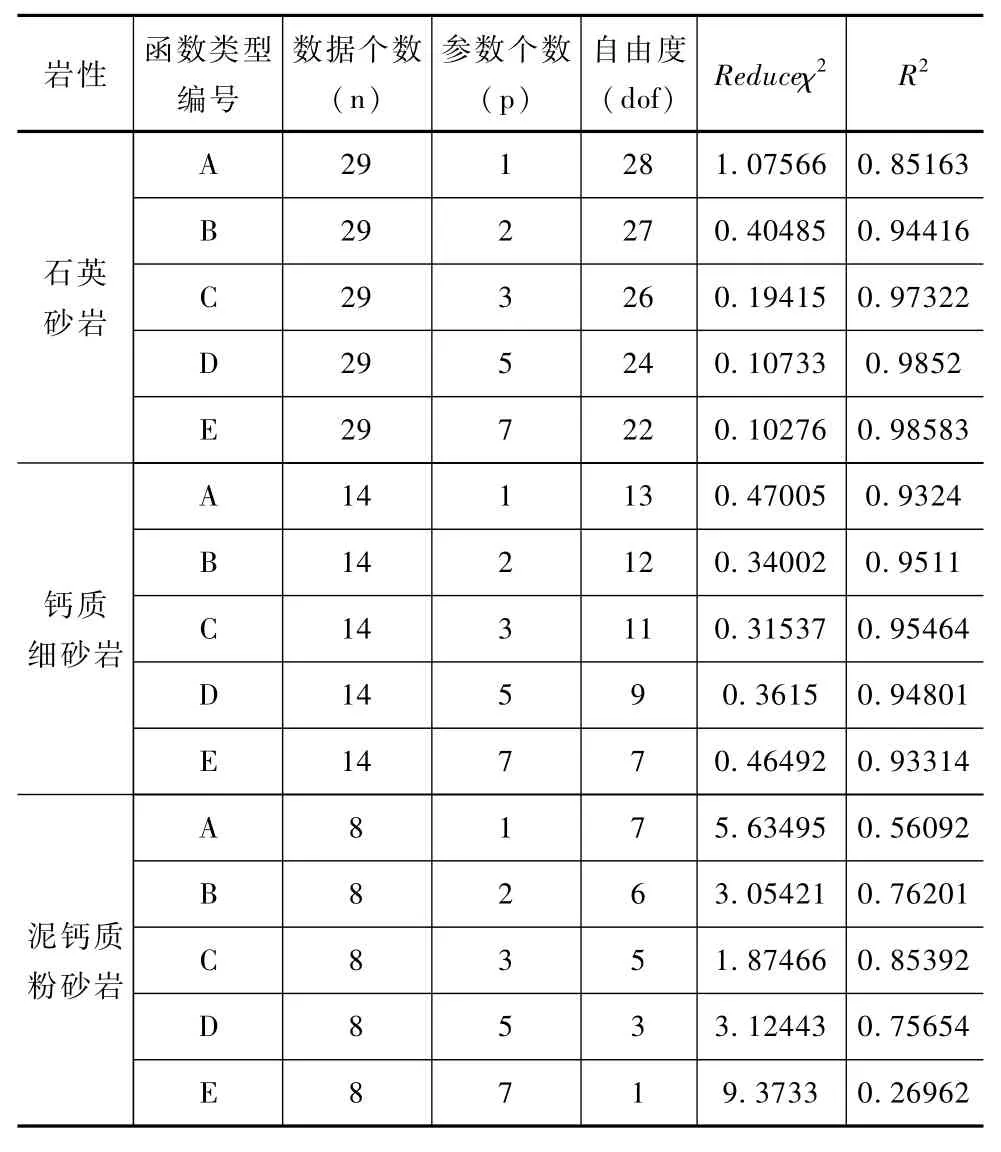
表1 波速与变形模量相关关系参数

将石英砂岩、钙质细砂岩、泥钙质粉砂岩3种岩体的变形模量和波速，按式（10）～（12）指数函数拟合的曲线如图1～3所示。从图1、2可以看出，石英砂岩和钙质细砂岩式（10）函数形式变形模量值整体偏大；在大波速值范围内，对应的变形模量偏小。式（11）函数形式在小波速和大波速范围内，对应的变形模量值均偏小。式（12）函数居于试验数据中心位置。从图3可以看出，泥钙质粉砂岩式（10）函数形式变形模量值整体偏大；在大波速值范围内，对应的变形模量值偏小。式（11）函数形式在小波速范围内，对应的变形模量值偏小；大部分波速对应的变形模量值与式（12）接近。式（12）函数居于试验数据中心位置。因此，根据变形模量与波速相关曲线对比分析1阶，递增指数函数最优。

根据上述图、表分析，得到这样的结论，即石门坎水电站坝基岩体变形模量与声波速度，按式（12）1阶递增指数函数拟合最优。石英砂岩岩体变形模量与波速相关关系为Em=2.61925+ 0.00659eVp/652.41138，钙质细砂岩岩体变形模量与波速相关关系为Em=3.28024+1.07558E-6eVp/260.33224，泥钙质粉砂岩岩体变形模量与波速相关关系为Em= 0.7276+0.2907eVp/1409.286。

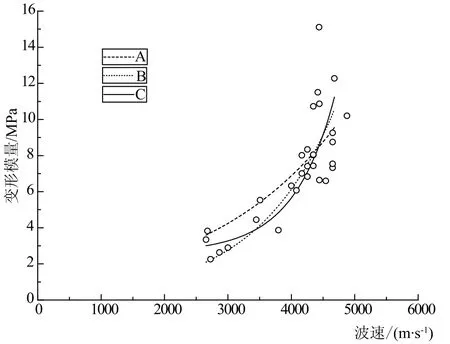
图1 石英砂岩变形模量与波速关系曲线

图2 钙质细砂岩变形模量与波速关系曲线

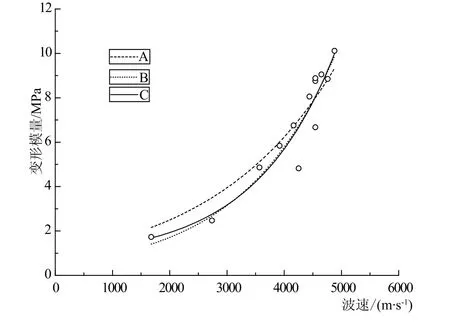
图3 泥钙质粉砂岩变形模量与波速关系曲线

上述为坝基开挖后岩体变形模量与声波波速的1阶递增指数函数的拟合。同样，该函数形式仍可用于拟合坝基岩体固结灌浆后岩体的变形模量与声波波速之间的相关关系，并根据其拟合出来的关系式制定坝基固结灌浆验收标准。

5 结论

变形模量是水利水电工程勘察设计中非常重要的力学指标。通过对变形模量与波速之间关系式、关系曲线进行分析，得出如下结论：岩体变形模量与波速相关关系为非线性；岩体变形模量与波速相关关系中，指数函数形式最为合适；变形模量与波速的5种指数函数形式中，1阶递增指数函数为最优。

［1］BARTONN.SomenewQ-valuecorrelationstoassistinsitecharacterisationandtunneldesign［J］.InternationalJournalofRockMechanics&MiningSciences，2002（39）：185-216.

［2］吴兴春，王思敬，丁恩保.岩体变形模量随深度的变化关系［J］.岩石力学与工程学报，1998，17（05）：487-492.

［3］冯国栋.姚河坝水电站岩体纵波波速与静变形模量相关关系的探讨［J］.水电工程研究，1993（01）：49-54.

［4］李维树，黄志鹏，谭新.水电工程岩体变形模量与波速相关性研究及应用［J］.岩石力学与工程学报，2010，29（Z1）.

［5］李维树，鲁先元等.三峡工程坝区工程岩体变形参数的动静特性研究［J］.地下空间，1999，19（04）.

［6］李维树，彭朝全，张仕光.乌江构皮滩水电站坝基岩体变形参数取值方法［J］.地下空间，2004，24（02）.

［7］李伟，沈蓉，古兴伟，等.小湾水电站坝址区岩体变形特性研究［C］.第一届中国水利水电岩土力学与工程学术讨论会论文集，2006.

［8］陈书文，许仙娥.固结灌浆后岩体变形模量的确定方法［J］.长江科学院院报，2014，31（01）.

TU459+.3

A

1672-2469（2015）12-0049-03

10.3969/j.issn.1672-2469.2015.12.018

李 雷（1969年—），男，高级工程师。