一类Lienard方程零解的全局稳定性
符策红,李 武
(1.海南软件职业技术学院 信息管理系,海南 琼海 571400;2.琼山华侨中学,海南 海口 571100)
一类Lienard方程零解的全局稳定性
符策红1,李 武2
(1.海南软件职业技术学院 信息管理系,海南 琼海 571400;2.琼山华侨中学,海南 海口 571100)
利用构造李雅普诺夫函数方法证明了一类Lienard方程的零解的全局稳定性.
Lienard方程;李雅普诺夫函数;全局稳定
1 引言及引理
著名的Lienard方程
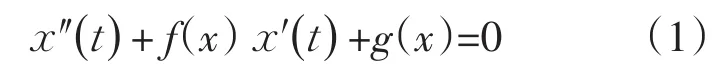
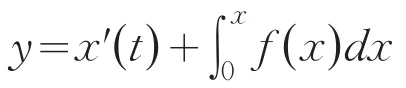
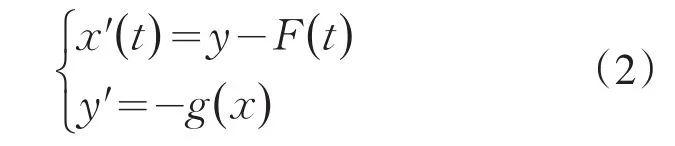
因其具有广泛的实际背景,人们对其研究一直怀着强烈的兴趣,并取得了相当丰富的结果[1-3].
引理1[1]若系统(2)满足
(a1)xg(x)>0,当x≠0时,
(b1)xF(x)>0,当x≠0时,
(c1)
那么,系统(2)的零解为全局稳定.
引理2[2-3]若系统(2)满足
(a2)xg(x)>0,当x≠0时,
(b2)xF(x)>0,当x≠0时,
(c2)
那么系统(2)的零解为全局稳定.
对于系统
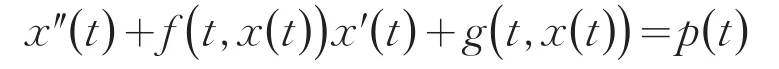
的大部分研究集中在周期解的问题上,并取得显著成果[4-7].本文从引理1和引理2入手,证明系统(3)的零解的全局稳定性.
2 主要结果
考虑Lienard方程

满足g(0,x(0))=0,f(t,x(t)),g(t,x(t))在R2上均连续.对(3)作Lienard变化
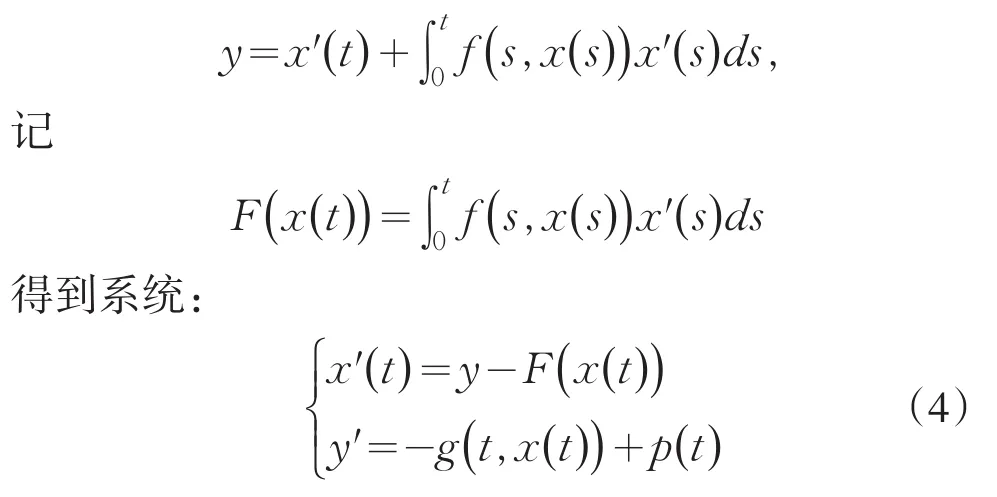
定理1 若系统满足条件:
(A1)x(t)[g(t,x(t))-p(t)]>0,当x(t)≠0时,
(A2)x(t)F(x(t))>0,当x(t)≠0时,
(A3)存在数列xn→+∞,→-∞使得

则系统(4)的零解为全局稳定.
证明 作系统(4)的李雅普诺夫函数:
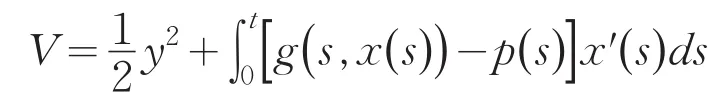
所以有:

是正定的,即:V′0,并且在直线y=0除了坐标原点外,不包含整条轨线.
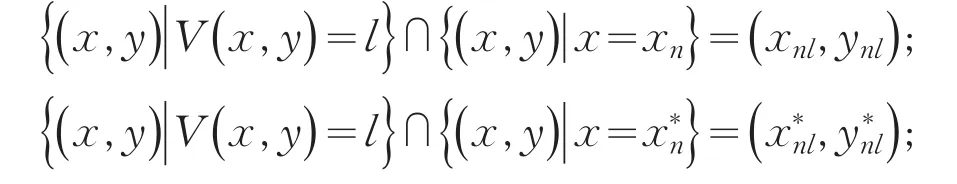
其中满足ynl
因为V′0,所以轨迹要从区域D内离开,就必须通过边界x=xn,x=但是在x=xn上有:
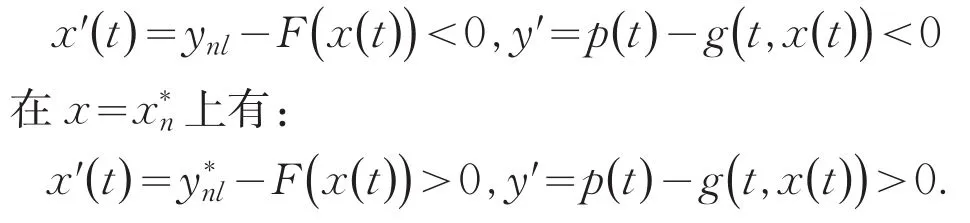
所以,轨迹经过边界x=xn,x=时候走向都是从外到里,即系统(4)的每一个正半轨都是有界的,定理1得证.
定理2 若系统(4)满足条件:
(A1)x(t)[g(t,x(t))-p(t)]>0,当x(t)≠0时
(A2)x(t)F(x(t))>0,当x(t)≠0时
(A4)∃xn→+∞,→-∞使得
则系统(4)的零解为全局稳定.
证明 条件(A4)满足至少有下面一个条件成立:
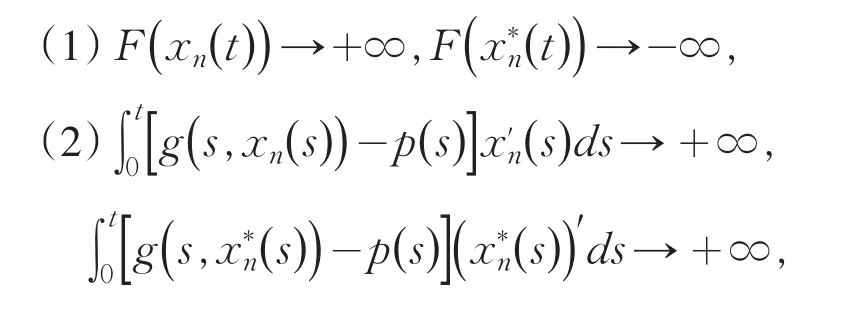
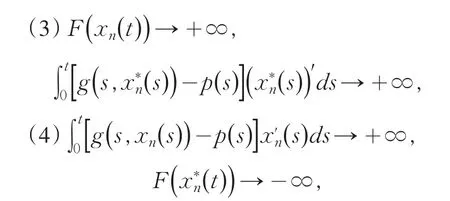
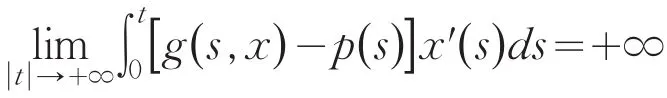
理2得到系统(4)的零解为全局稳定.
当条件(3)成立时取区域
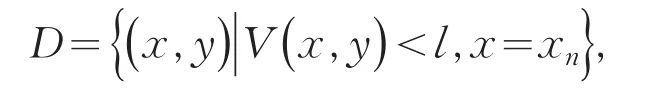
对于∀l,xn因为V是正定的,所以∃l>0,xn使得∀P(x,y)∈D有:
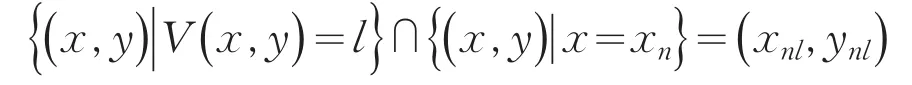
并且满足ynl 因为V′0,所以轨迹要从区域D内离开,就必须通过边界x=xn但是在x=xn上有: 所以轨迹经过边界x=xn时候走向都是从外到里即系统(4)的每一个正半轨都是有界的即系统(4)的零解为全局稳定.同理可证,当条件(4)满足时,取,可得到系统(4)的零解为全局稳,定理2得证. [1]李曾淑,王慕秋.关于Lienard方程零解的全局稳定性[J].数学研究与评论,1985,5(2):67-70. [2]秦元勋,王慕秋,王联.运动稳定性理论与应用[M].北京:科学出版社,1981. [3]Vilari G.Periodic solutions of Lienard equation[J].J Math Anal Appl,1982,86:376-386. [4]Vilari G.On the existence of periodic solutions of the Lien⁃ard equation[J].Nonlinear Anal,1983,7:71-78. [5]Mawhin J L,Ward J R.Periodic solutions of some forced Lienard differential equation at resonance[J].Arch Math, 1983,41:337-351. [6]彭世国.时滞的Lienard型方程的周期解[J].工程数学学报,2004,21(3):463-466. [7]朱宏伟,王梅.具有两个偏差变元的广义Lienard型方程周期解得存在性[J].青岛大学学报:自然科学版,2011,22(1):5-9. [8]Guo D.Theory of Functional Analysis[M].Jinan:Shandong Technology and Scienece Publishing House,2001. 责任编辑:毕和平 Global Stability of the Zero Solution for a Class of Lienard Equation FU Cehong1,LI Wu2 The global stability of the zero solution for a class of Lienard equation was proved by using Lyapunov function method. Lienard equation;Lyapunov function;global stability O 175 A 1674-4942(2015)03-0255-02 2015-05-08 海南省自然基金项目(114010)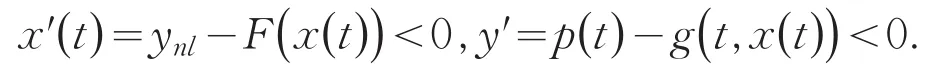
(1.Department of Information Management,Hainan College of Software Technology,Qionghai 571400,China;2.Qiongshan Overseas Chinese Middle School,Haikou 571100,China)

