常微分方程教学中的一些思考
徐家发
(重庆师范大学 数学科学学院,重庆 401331)
常微分方程教学中的一些思考
徐家发
(重庆师范大学 数学科学学院,重庆 401331)
给出几类多点、积分边值问题转化为相应的积分方程的方法,并讨论这些问题与其相应的零边值问题的关系.
常微分方程;边值问题;积分方程
通常把积分号下出现未知函数的方程称为积分方程.未知函数以线性形式出现的方程称为线性积分方程,否则,称为非线性积分方程[1-2].由于实际发展的需要,目前研究较多的是所谓的Hammerstein型非线性积分方程:

其中G(x,y)和f(y,u)都是其变元的已知函数,G(x,y)被称为格林函数.
众所周知,在讨论微分方程边值问题解的存在性时,通常的做法是将其转化为相对应的积分方程,然后借助非线性泛函分析中的拓扑方法或者变分方法获得积分方程解的存在性,运用等价性获得原微分方程解的存在性[3-4].所以,将微分方程转化为对应的积分方程显得尤为重要.例如,二阶Dirichlet边值问题

等价的积分方程为

其中
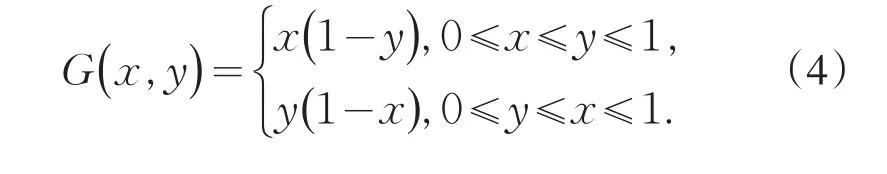
本文主要讨论如何将各种微分方程(包括分数阶方程)转化为对应的积分方程,并讨论多点、积分边值问题与对应的零边值问题的关系.通过两者关系的比较,做到由易入难、由简入繁,这有助于激发学生的学习热情,培养学生的创新能力.
1 整数阶微分方程
以下首先给出问题(2)转化为积分方程(3)的方法,并讨论三点边值问题
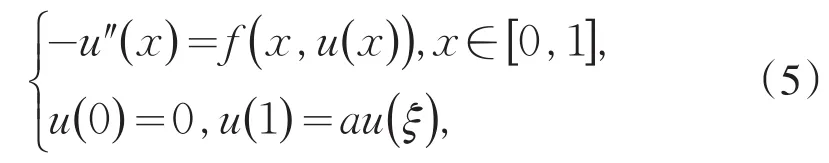
和积分边值问题

易见(2)是(5)的特殊情况,以下给出(5)的等价积分方程.根据常微分方程的基本知识,我们有
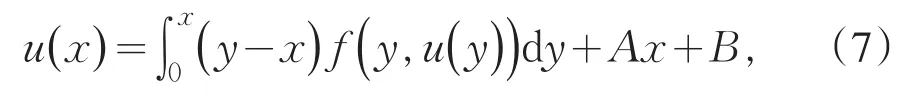
其中A,B是常数.事实上,对(7)式两边求导可得
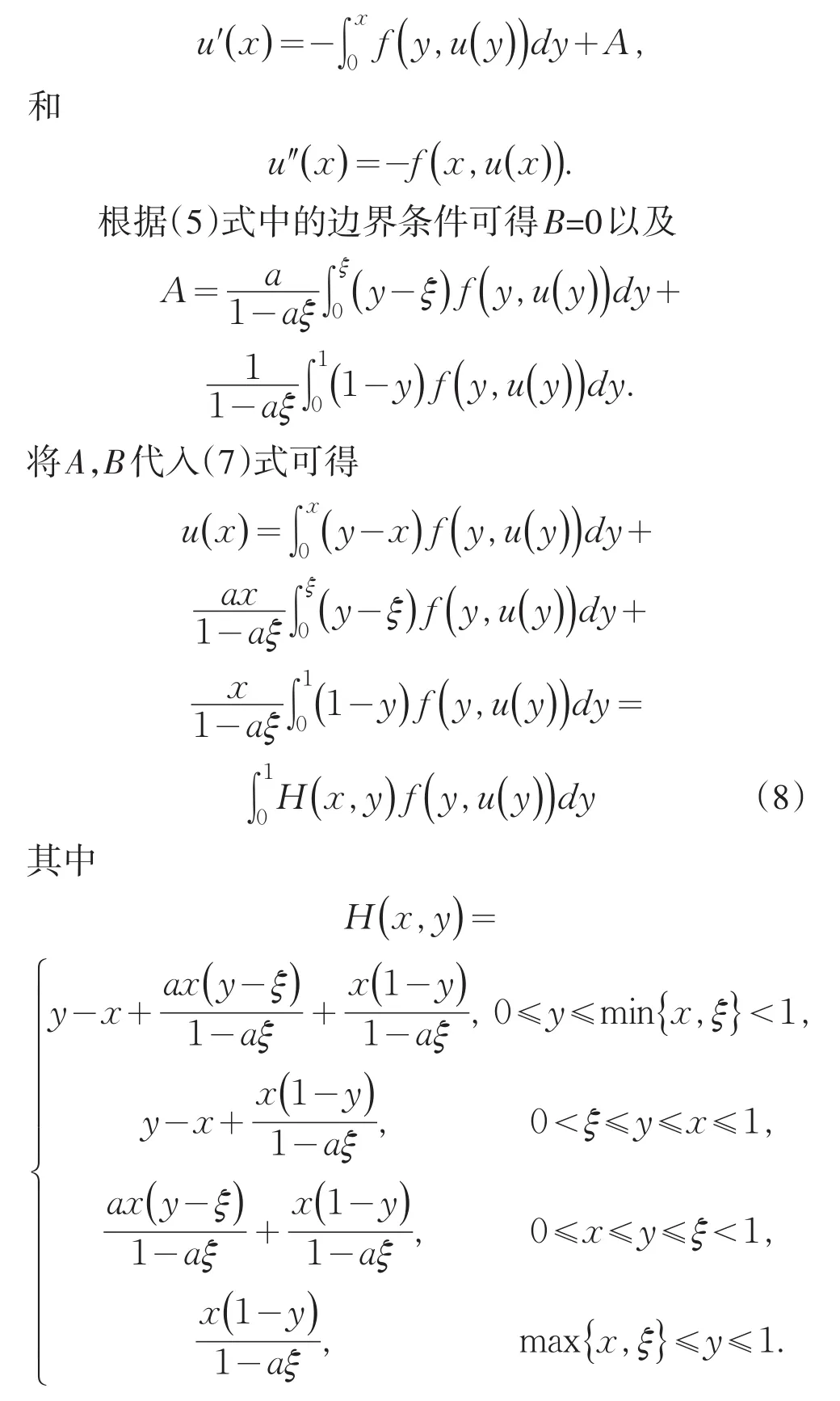
显然若a=0,(5)和(2)是同样的.那么试问:如此繁复的格林函数H(x,y)与相对简单的格林函数G(x,y)有何关系?能否用G(x,y)来表示H(x,y)?
在(8)式的计算中,若做如下处理

在上式最后两行中,将前两个积分合并,将第三个、第四个积分合并,可得
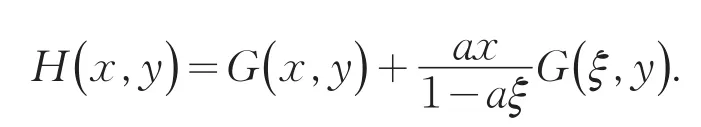
由此可见,H(x,y)由G(x,y)来生成,从而若将(5)看成(2)的扰动,新的格林函数H(x,y)仅需在原有的格林函数G(x,y)的基础上加上它的一个变形.
针对积分边值问题(6),我们先计算常数A,B由u(0)=0可知B=0.从而根据(7)式,有
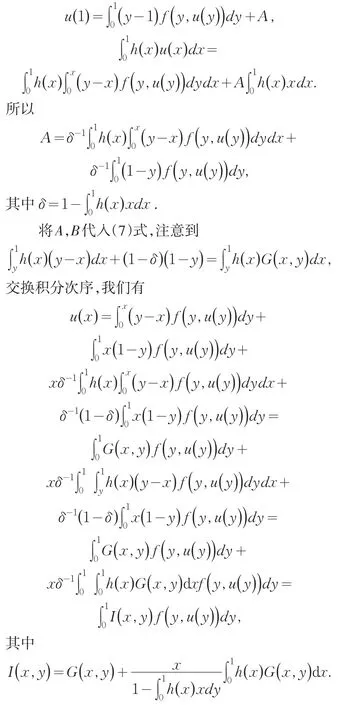
显然I(x,y)也是在原有的G(x,y)的基础上加上它的一个变形.
2 分数阶微分方程
分数阶微分方程是传统的整数阶微分方程的推广,分数阶微积分主要是研究任意阶积分和微分的数学性质及其应用.数学家们研究发现用新的分数阶模型能更精确地模拟现实问题,分数阶微分方程非常适合用来描述现实生活中具有记忆和遗传特性的问题,文献[5]中列举了大量的分数阶方程在应用中的实例,因此研究这类方程具有非常重要的理论意义和应用价值.
以下用具体的分数阶微分方程来说明在计算格林函数时,亦可采用第二部分中所提到的方法.首先给出本文所使用的Riemann-Liouville分数阶的定义及相关知识.
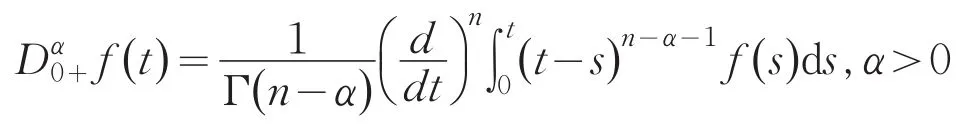

引理1[8]若u,,则

其中N是大于或等于α的最小整数.
定理1 令y∈C[0,1],则分数阶边值问题
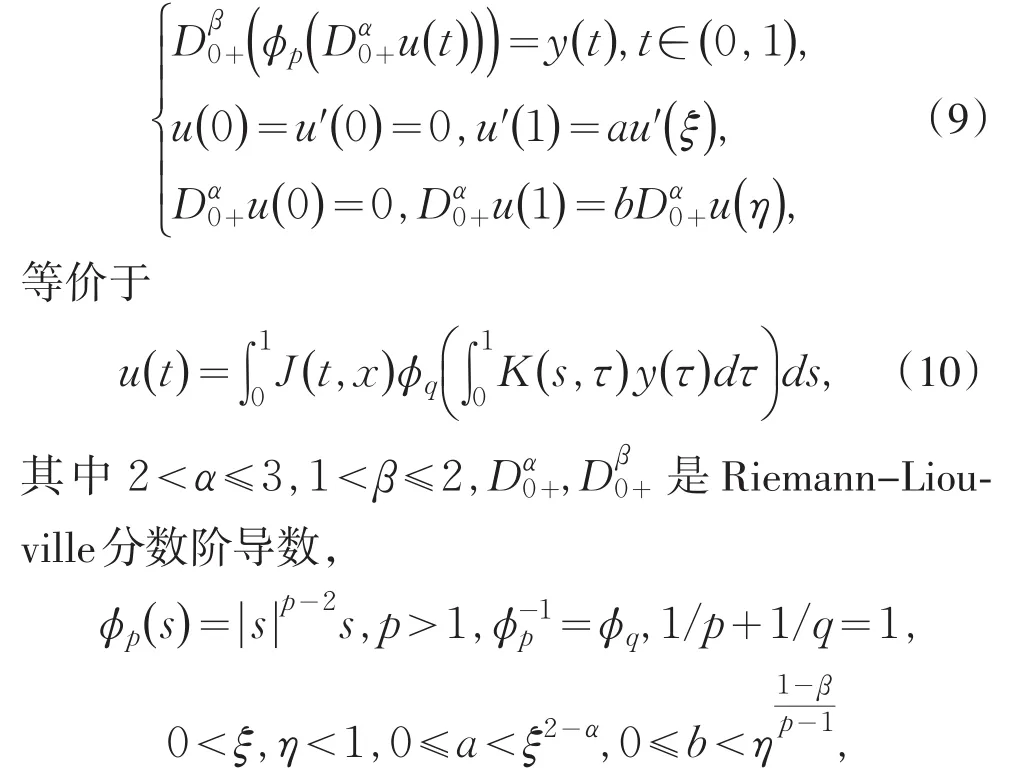
格林函数J,K见证明过程.
证明 根据引理3可得




3 结束语
与零边值问题相比较而言,处理多点、积分边值问题更为困难,但由本文提供的方法可以看出,将多点、积分边值看成是零边值情形的扰动,它们的格林函数实际上就是零边值基础上多加一个变形,所获结果更为简洁.
[1]传璋,侯宗仪,李明忠.积分方程论及其应用[M].上海:上海科学技术出版社,1987.
[2]路见可,钟寿国.积分方程论[M].武汉:武汉大学出版社, 2008.
[3]葛渭高.非线性常微分方程边值问题[M].北京:科学出版社,2007.
[4]白占兵.分数阶微分方程边值问题理论及应用[M].北京:中国科学技术出版社,2013.
[5]郑祖庥.分数微分方程的发展和应用[J].徐州师范大学学报,2008,26(2):1-10.
[6]Podlubny I.Fractional Differential Equations,Mathematics in Science and Engineering[M].New York:Academic Press, 1999.
[7]Samko S,Kilbas A,Marichev O.Fractional Integrals and De⁃rivatives:Theory and Applications[M].Yverdon:Gordon and Breach,1993.
[8]Bai Z,Lü H.Positive solutions for boundary value problem of nonlinear fractional differential equation[J].J Math Anal Appl,2005,311(2):495-505.
责任编辑:刘 红
Some Considerations in Teaching of Ordinary Differential Equations
XU Jiafa
(School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China)
In this paper we offer some methods of transforming multi-point and integral boundary value problems into the corresponding integral equations and discuss the relationships between these problems and zero boundary value problems.
ordinary differential equations;boundary value problems;integral equations
O 175.1
A
1674-4942(2015)03-0346-04
2015-07-08
国家自然科学基金资助项目(11371117);重庆师范大学基金项目资助(15XLB011)

