基于改进 PSO 算法的物流网点选址研究

邵玉华，贾玉卫，陈帝霖

SHAO Yu-hua1，JIA Yu-wei2，CHEN Di-lin2

（1.昆明铁路局 货运处，云南 昆明 650000；2.西南交通大学 交通运输与物流学院，四川 成都

610031）

(1.Freight Transport Department， Kunming Railway Administration， Kunming 650000， Yunnan， China； 2.School of Transportation and Logistics， Southwest Jiaotong University， Chengdu 610031， Sichuan， China)

基于改进 PSO 算法的物流网点选址研究

邵玉华1，贾玉卫2，陈帝霖2

SHAO Yu-hua1，JIA Yu-wei2，CHEN Di-lin2

（1.昆明铁路局 货运处，云南 昆明 650000；2.西南交通大学 交通运输与物流学院，四川 成都

610031）

(1.Freight Transport Department， Kunming Railway Administration， Kunming 650000， Yunnan， China； 2.School of Transportation and Logistics， Southwest Jiaotong University， Chengdu 610031， Sichuan， China)

在阐述目前设施选址模型和快递网点布局研究的基础上，针对物流网点整体偏少并且布局不合理的问题，以建立物流网点所需满足时效性及经济成本最小化要求为目标构建模型，采用改进后 P-中值选址模型对物流网点在某区域的选址问题进行研究，在标准粒子群算法的基础上采用 CUDA 并行编程模型求解以提高计算速度，最后通过某区域物流网点的选址实例验证算法的可行性。

物流网点；P-中值模型；粒子群算法；CUDA 并行编程模型

物流网点选址问题属于设施选址问题之一，可以通过借鉴设施选址方法来研究物流网点选址问题。目前，国内外学者对设施选址模型和快递网点布局进行了诸多研究，Hakimi S L[1]用 P-中值模型来研究如何使需求点的需求量与服务站的距离乘积之和最小；Carbone R[2]对 P-中值问题进行改进，研究需求量服从多变量正态分布且带机会约束的情形，建立非线性模型来解决不确定下公共设施网络的选址问题；杨茂盛等[3]在用重心法得到备选地点的基础上，引用离散模型解决配送中心的最佳地点问题。对于算法的研究，学者最初采用线性规划、非线性规划和网络规划等较简单的算法，随着模型的复杂化，算法方面也开始采用遗传算法[4]、蚁群优化[5]、模拟退火[6]等智能算法。上述研究大部分假设候选地点个数为已知，而实际在选址初期不可能准确确定建立个数，必须通过不断测算验证，推算出建立设施的个数。基于上述研究存在的问题，考虑不明确规定选址个数，而仅将其作为上层目标，建立 P-中值选址模型，下层目标在上层目标的基础上，求得总运输费用 (包括运输费用、网点建设费用和维护费用等) 最低。

1　模型构建

目前物流网点总体分布偏少并且客户分布分散不利于研究，首先对客户进行聚类分析，将一定区域内分散的客户抽象为 1 个具体的发生点。假设发生点已知，物流网点根据发生的分布建立一定数量的候选网点，物流网点选址的目的是在配送成本最小的情况下，尽可能少地选择物流网点。因此，物流网点选址问题可以进行以下描述：给定发生点集合和候选网点集合，已知发生点的数目，运量及发生点与候选网点之间的距离，在总配送成本最小的方案下，确定合理的物流网点数目。

假设有 m 个发生点，n 个备选物流网点，需要从 n 个备选物流网点中选择 P 个网点来满足该区域所有发生点的需求，P 的数目不确定；物流网点的修建有建造费用；每个发生点只能由 1 个物流网点为其服务；发生点数目及每个发生点的运量固定，所有备选物流网点的服务能力已知；每个备选物流网点的最大吞吐量不超过其最大服务能力。根据分析，问题中包含 2 个求解目标，网点数目和网点的选址均为未知，并且选址结果基于网点数目，针对该情况建立双层模型来分别表示 2 个求解目标，即总的网点数目最小和网点选址目标总配送成本最低，其中后者的求解建立在前者解的基础之上。具体模型计算公式为

式中：L 为基本配送距离；wi为发生点 i 的货运量；δj为备选网点的固定成本，包括租金、货运管理人员工资；sj为备选网点 j 的最大服务能力；cij为发生点 i 与备选网点 j 间在基本里程内的运输费用；c'ij为超出基本费用的费率；dij为发生点 i 与备选网点 j 之间的距离；P 为拟建立的网点个数；λ，μ为参数变量；

⑶ 式表示备选网点的最大吞吐量不能超过该网点的最大服务能力；⑷ 式表示 1 个发生点只能有1 个物流网点提供服务；⑸ 式表示拟建立物流网点至少为 1 个；⑹ 式表示保证发送点必须由选中的物流网点提供服务。

2　试验环境及求解算法

粒子群优化算法是 Kennedy 和 Eberhart 受到真实世界中鸟群寻找食物飞行行为启发，于 1995 年提出的智能优化算法[7]。由于该算法具有收敛速度快、寻优能力强、参数设置简单等优点，目前已经成为选址问题求解的主流算法。在实际情况中，当物流网点较多时，粒子本身信息和粒子极值信息常占有较大优势，致使算法容易陷入局部最优解。针对该问题设计新型的粒子编码方式和混沌变异算子，以克服粒子陷入局部最优解的问题，同时采用 CUDA 并行编程模型分离出算法的局部性和并行性，提高计算速度。

2.1粒子编码

2.2混沌变异操作

混沌状态在自然现象和社会现象中广泛存在，由于其具有随机性、遍历性和规律性等性质，使混沌运动能够在一定范围内按照其自身“规律”不重复遍历所有状态，这种遍历性特点可以作为搜索过程中避免陷入局部极值的优化机制，因而构造混沌变异算子如下[8]。

2.3算法步骤

步骤 1：对整个算法流程进行分析，根据算法的特性采用 CUDA 并行编程模型，分离出算法的局部性和并行性。

步骤 2：设定粒子群规模 N，阀值 thre = 0.20，初始化粒子群中每个粒子的位置为第 n 个备选网点被选中的概率，可以通过居民调查法或专家打分获取。

步骤 4：计算每个需求点到所有备选网点的距离，选择其中最小值组成距离矩阵 Bm×n，将解向量与矩阵 Bm×n代入到 ⑵ 式中，求得的函数值即为粒子适应值。

步骤 5：如果目前的适应度值小于之前的 local-Best1，localBest2，…，localBestn 适应度值，则用目前的适应度值代替 localBest1，localBest2，…，localBestn 适应度值，并得到新的个体最优网点，新的最优网点进行全局交流得到新的 globalBest 适应度值，即得到目前最优网点。

步骤 6：如果 globalBest[n]-globalBest[n-1]≤thre，实验结束；反之，继续进化候选站点。

步骤 8：对粒子进行自适应混沌操作，并且转入步骤 5。

步骤 9：计算结束。

3　实例分析

3.1算例描述

假定某区域需要新建网点来满足该区域的需求，备选网点集为 N1—N5，发生点为 M1—M10，该区域备选网点的基本作业里程为 10 km，在基本里程内的单位运输费率为 20 元/t，超出基本里程的运输费率为 0.5 元/t。备选网点位置及服务能力、发生点的位置及发生量、备选网点最大服务能力及固定成本分别如表1—表3 所示。各备选网点及发生点位置如图1 所示。

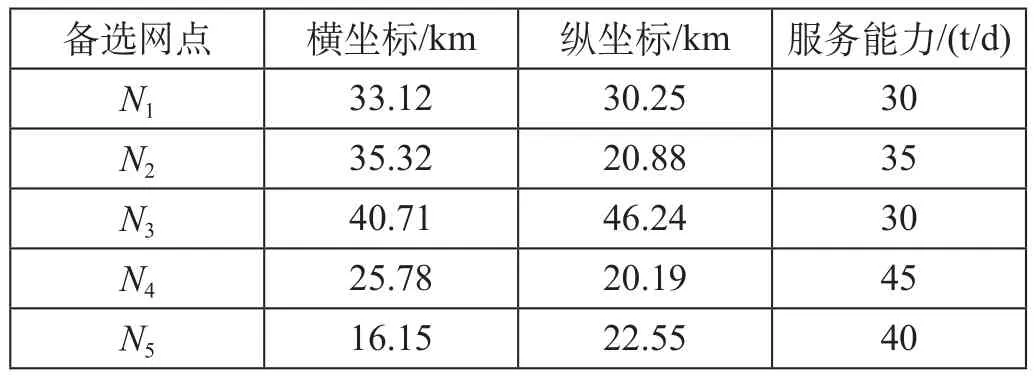
表1　备选网点位置及服务能力

表2　发生点位置及发生量

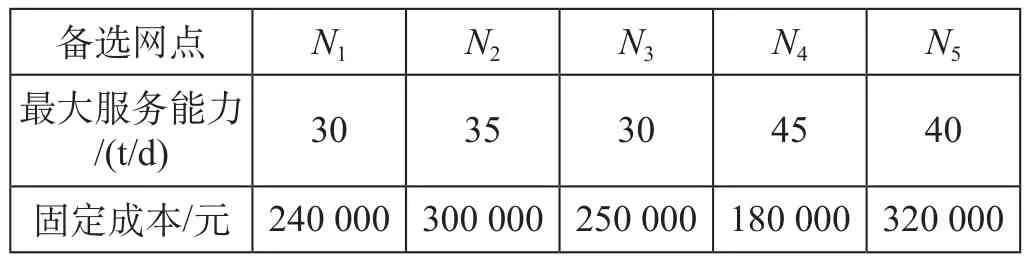
表3　备选网点最大服务能力及固定成本

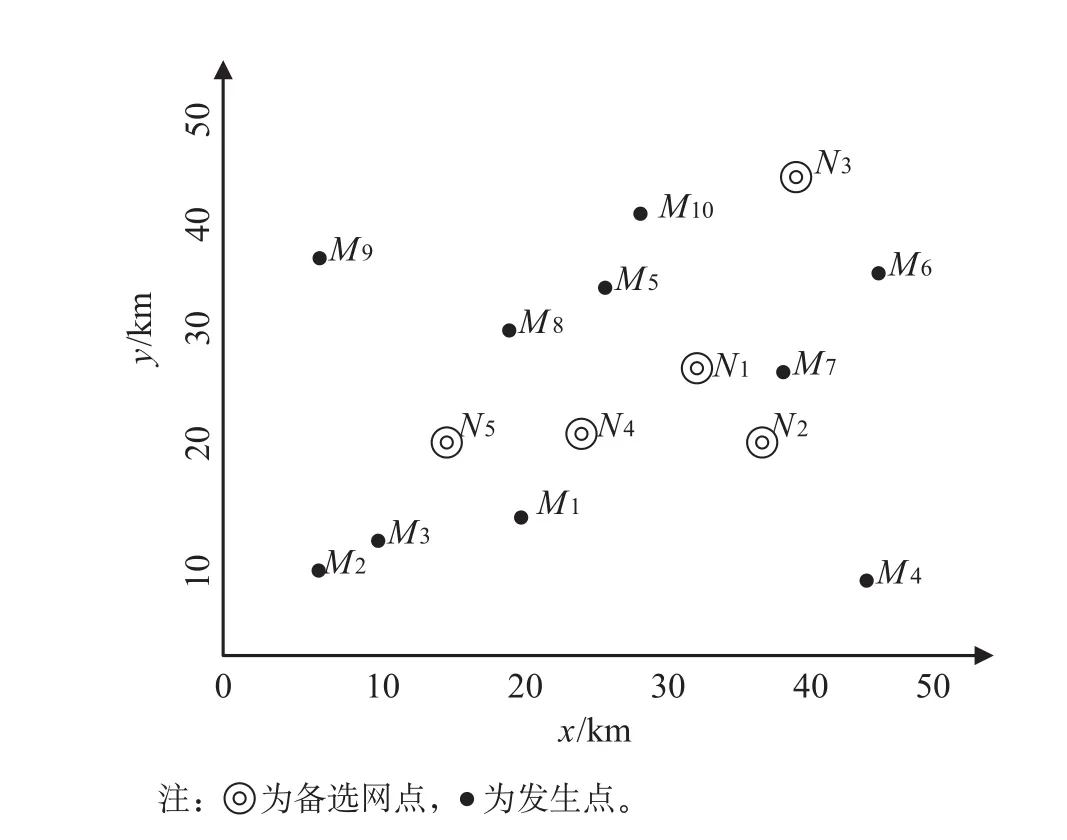
图1　备选网点及发生点位置示意图

3.2结果分析

算法的参数设置如下。粒子群的规模为10，学习参数 w，权重 r1，r2均为 1；实验结束采用阀值设定 thre = 0.20，前后 Fitness 差值小于该阀值时实验结束。改进 PSO 计算的选址结果如表4 所示。

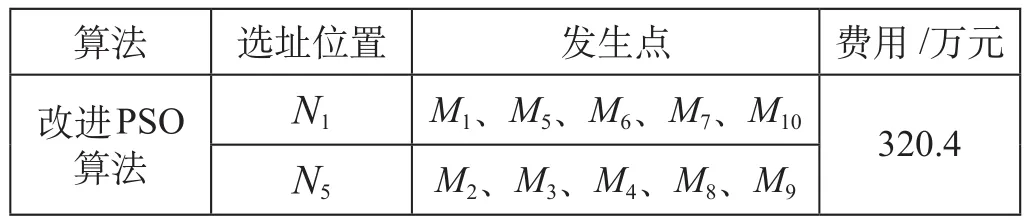
表4　选址结果

由表4 可知，当发生点 M1、M5、M6、M7、M10选择网点 N1，发生点 M2、M3、M4、M8、M9选择网点 N5时，总运输费用最小为 320.4 万元。此时，发生点 M1、M5、M6、M7、M10的需求总和为18 t，在网点 N1的服务能力范围内；发生点 M2、M3、M4、M8、M9的需求总和为 17 t，在网点 N5的服务能力范围内。结果表明，该模型有效可行。

4　结束语

通过研究物流网点选址的问题，将一定区域内分散的客户抽象为具体的发生点，研究 1 种备选网点已知，但网点选择数目不确定的 P-中值选址模型，在算法的求解中，根据改进后 P-中值模型的特点，设计新型的粒子编码方式和混沌变异算子，解决粒子容易陷入局部收敛的问题，采用 CUDA 并行编程模型，提高计算速度，可以应用于计算物流网点选址的问题，该研究对目前物流网点的选址有一定的实际意义和参考价值。但是，还应结合客户时效性问题进行研究，如果加入客户的时间满意度函数，模型将更切合实际。

[1] Hakimi S L. Optimum Locations of Switching Centers and the Absolute Centers and Medians of a Graph[J]. Operations Research，1964，12(3)：450-459.

[2] Carbone R. Public Facilities Location under Stochastic Demand[J]. Infor，1974，12(3)：261-270.

[3] 杨茂盛，姜 华. 基于重心法与离散模型的配送中心选址研究[J]. 铁道运输与经济，2007，29(7)：68-70. YANG Mao-sheng，JIANG Hua. Research on Location Selection of Distribution Center based on Gravity Method and Discrete Model[J]. Railway Transport and Economy，2007，29(7)：68-70.

[4] 王春燕，张 华. 遗传算法在配送中心选址中的应用[J]. 物流科技，2007(4)：111-113. WANG Chun-yan，ZHANG Hua. Application of Genetic Algorithm to Location of Distribution Center[J]. Logistics Sci-Tech，2007(4)：111-113.

[5] 秦 固. 基于蚁群优化的多物流配送中心选址算法[J]. 系统工程理论与实践，2006(4)：120-124. QIN Gu. Logistics Distribution Center Allocation based on Ant Colony Optimization[J]. Systems Engineering-Theory & Price，2006(4)：120-124.

[6] 姜 山. 基于模拟退火算法的应急系统选址优化[J]. 物流技术，2011(9)：142-143. JIANG Shan. Location Optimization for Emergency Response System based on Simulated Annealing Algorithm[J]. Logistics Techlonogy，2011(9)：142-143.

[7] 彭莉娟，吴 鹍，余 静. 机场跑道最大容量评估模型的研究[J]. 四川大学学报：自然科学版，2006，43(5)：1018-1022. PENG Li-juan，WU Kun，YU Jing. The Design and Research of Airport Maximal Capacity Estimation Model[J]. Journal of Sichuan University：Natural Science Edition，2006，43(5)：1018-1022.

[8] 林玉娥，顾国昌. 一种基于混沌变异的粒子群算法[C]//黑龙江省计算机学会. 黑龙江省计算机学会 2007 年学术交流年会论文集. 哈尔滨：哈尔滨工程大学，2007：332.

责任编辑：吴文娟

Study on Location of Logistic Network based on Improved PSO

Based on expounding the current study on facility location model and distribution of express delivery network, targeting with the problems existing in logistic network such as less networks on the whole and unreasonable distribution, the modeling is made by taking the minimized timeliness and economic cost which logistic network construction need satisfying as the objects, then the location of logistic network in certain zone is studied by using improved P-median location model, and CUDA parallel programming is applied to make solution based on particle swarm optimization (PSO), in the end, the feasibility of PSO is validated through actual location example of a logistic network in certain zone.

Logistic Network; P-median Model; PSO; CUDA Parallel Programming

1003-1421(2015)12-0022-04

F259.22

A

10.16668/j.cnki.issn.1003-1421.2015.12.05

2015-11-05

中国铁路总公司科技研究开发计划课题(2014X009-J)