基于人工股票市场的财富分布及演化研究
高 言,李昭辉
(1.中央财经大学金融学院金融工程系,北京100081;2.帝国理工大学商学院,伦敦SW11 2DL)
0 引言
随着复杂性科学和计算机模拟技术的发展,自20世纪90年代起,自下而上的多主体建模(基于主体的建模)方法开始逐步被引入金融领域,主要应用于金融市场的微观结构和交易策略的研究,并因其依靠数学建模和人工模拟的方法创新成为金融市场研究的新热点[1-5]。
股票市场具有买卖双方均不止一人的多对多的市场结构,广泛采用双向拍卖机制进行交易,是一个典型的具有自适应性的复杂系统[6]。与传统金融理论的演绎推理方法不同,多主体模型采用自下而上的归纳推理,强调经济主体的个体差异性,能够很好地刻画股票市场中个体行为因其自身禀赋(如信息获取及处理的能力、风险偏好等)的不同而表现出的异质性,模拟真实市场中的价格形成机制,构建个体与个体之间相互联系、个体与整体市场之间相互影响的动态系统,为研究股票市场这一自适应系统的复杂性特征提供了一个可行路径。
目前多主体建模在股票市场的研究按照其目的大致分为3类。第1类是通过多主体的动态模拟,辅以真人实验,并与传统均衡理论相对照来研究股市中价格趋于均衡价值的收敛速度,并基于此对市场资源的配置效率进行探讨[7-8]。该类研究主要从两个角度展开,其一是策略比较的角度,如零智能模型及其拓展[9-11];其二是结合策略并着重于不同价格形成机制比较的角度[12]。第2类关注于主体是否有报价的最优策略及主体的学习过程[13-15]。第3类则通过对市场中真实投资者行为的细致刻画搭建人工股票市场平台,展现真实市场所拥有的收益率尖峰胖尾、波动聚集等典型事实,并在此基础上探讨市场的交易规则对价格波动与市场稳定性等的影响[16-24]。
综上,多主体建模在股票市场的研究多集中于资源分配的效率,而关注资源配置公平的研究较少。针对公平性问题,具有代表性的便是社会收入与财富分布的研究。早在1897年,帕累托就曾基于对多个国家收入分配的观测提出了收入分布的尾部(高收入部分)呈现出较前端(中低收入部分)更加不均等的现象,总结了尾部收入服从幂律分布的结论,其幂指数被称为帕累托指数[25]。之后,大量学者纷纷收集各个国家的收入数据对这一结论进行印证[26]。同时财富作为收入在一段时间的累积也被证明其尾部同样服从幂律分布。如Levy等[27]利用1996年Forbes公布的美国最富有400人的财产及排名,发现美国财富分布的尾部可以用幂律分布拟合,其帕累托指数约为1.36。Adrian等[28]利用同年的Forbes数据,发现英国财富分布的尾部可以用指数约为1.9的幂律分布拟合。Sinha[29]利用2002年Business公布的印度最富有125人的财富,发现其幂律分布的帕累托指数约为0.81。高建敏等[30]利用2003—2005年《福布斯》公布的中国大陆富人榜数据发现中国财富分布的尾部服从幂指数约为0.98-1.21的幂律分布。在数学上可以严格证明,当整体分布完全服从帕累托分布时,帕累托指数越小,整体分布的均等程度越低[31-33]。而实证研究表明中低财富(或收入)群体的非均等程度要低于高财富(或收入)群体服从的帕累托分布,一般服从对数正态分布或指数分布[29]。那么,用帕累托指数来测算整体财富(或收入)的非均等程度往往会得到高估的结论。而该指数的大小与整体财富(或收入)的非均等程度之间的对应关系也会由于中低财富(或收入)群体分布特征的不同而不同[34]。鉴于此,作为一个更一般化的指标,洛伦兹曲线刻画了累积财富(或收入)占比与累积人口占比的对应关系,由此测算的基尼系数(1922)[32]可以在不考虑分布的情景下给出整体财富分布非均等程度更为准确的衡量。然而,不论是帕累托指数还是基尼系数的测算,其收入或财富数据大多来自于个人的税收记录或财富排名,该数据来源既包含实体经济部门又包含金融市场。而就财富积累的过程和机制来看,实体经济与金融市场这两种不同的环境可能会对财富分布的特性及演化产生不同的影响。但受限于数据的可获得性,目前还没有专门针对(某一)金融市场的财富分布的实证研究。
本文拟基于多主体建模的方法,自下而上地构建贴近实际的人工股票市场,以此为平台,展现真实股票市场中收益率尖峰胖尾、波动聚集等典型事实特征,并弥补实证上缺少股市财富数据的缺陷,对股票市场中投资者的财富分布和演化进行初步探讨,除了关注尾部高财富群体的分布规律外,对整体财富分布也进行了基尼系数的测算。
1 模型设计
结合中国上海证券交易所的交易规则,本文设计了一个虚拟的人工股票市场,通过对微观投资者交易策略与行为的刻画来探索宏观上整体市场所涌现出的统计特征及投资者的财富演化。为了保持模型的简洁,假定市场中只有一支可以和现金交换的股票,股票在市场中的流通总数不变且无红利发放,现金的收益率为0(可以理解为投资者持续持有现金的时间较短且不确定而忽略其时间价值)。
1.1 基本市场框架
中国证券交易采用计算机集合竞价和连续竞价两种方式。由于集合竞价在每日交易中占据的时间较短,并且参与主体也有所不同。所以只关注于每日交易中的连续竞价过程,直接用前一天的收盘价作为当天开盘价的近似,并用最后一笔成交价格作为当日的收盘价格。
具体地,关注人工股票市场的T个交易日。在每个交易日,市场中的N个投资者按随机顺序进入,并根据自己对股票未来价格的预测提交订单。假定每个投资者每日有且仅有一次机会进入市场。这样以交易者的申报为间隔,每个交易日包含N个交易区间。市场根据投资者的申报按照价格优先与时间优先的顺序撮合成交。未成交的订单暂存在当日的指令簿中。在交易日结束时,仍未成交的订单会被清空。
1.2 交易参与主体——异质投资者
每日有N位投资者参与市场交易。与传统经济金融理论所假设的同质代理人不同,我们强调投资者的异质性。这里的异质性主要体现在投资者依据自身的不同禀赋对股票未来价格有不同的预测及策略行为。1.2.1 投资者的初始禀赋
投资者初始禀赋的不同在模型的初始设定时主要体现在两个方面,一是投资者的风险厌恶程度不同,以αi标识。它决定了投资者每次申购时拿出多少比例的现有可利用财富进行买卖报量,该比例假设服从均匀分布αi~U[α1,α2];二是投资者对信息资源的获取与处理能力不同。大致分为3类:1)能够获取较为准确的信息并有较强处理能力的机构投资者,体现在他们既能够得到上市公司股票的较为准确的价值信息vt,又掌握通过以往市场信息推导价格变动趋势的技术手段。2)仅能够利用股票价格的历史信息进行处理并推导未来价格变动趋势的趋势交易者。现实中利用市场历史信息进行技术交易的种类繁多,交易策略也很丰富。这里仅采用最常见的趋势交易作为初步探讨。3)不以股市盈利为目标的噪声交易者,该类交易者往往忽视股票市场中的所有信息,他们参与市场是为了流动性或其它便利性的需求。
事实上,不同投资者进入市场时的财富也不尽相同,而不同的财富会使得投资者可以进行的交易种类(如有些交易会有资金的门槛)及摩擦费用(如佣金、税收等)有所差异,这自然会增加模型的维度及复杂性。本文集中关注由于投资者对信息资源获取及处理能力不同而带来的财富演化及分布特性,所以在模型的初始设定中,赋予所有投资者相同的财富(由现金与股票构成)。
1.2.2 投资者的策略行为
1.2.2.1 投资者对未来价格的预测
依据投资者对信息资源的获取禀赋与处理能力的不同,分别阐述机构投资者、趋势交易者与噪声交易者3类不同投资者对未来价格的预测方式。
第1类是机构投资者。他们拥有最准确的信息资源——股票的价值vt,可以进行价值投资。该投资理念最早由格雷厄姆提出,其核心在于对企业价值的研究,认为股票价格会围绕其自身价值上下波动,即当股价低于(高)于价值时将会上涨(下跌)。据此,第i个机构投资者在第t日采取价值投资时对当日股票收盘价的预测pei,t为式(1)所示。

对于上市公司股票价值的确定存在很多争论,而这不是本文关注的重点,在此采取最一般的处理方式,假设股票的价值vt服从几何随机游走过程ln(vt)=ln(vt-1)+ηt,ηt为服从正态分布的随机噪声ηt~N(0,σ2η)。di1标识不同机构投资者对价格回复到价值速度快慢的不同看法,假设其服从均匀分布di1~U[dd1,du1]。eit标识机构投资者在获取价值信息时所受到的随机干扰,假设其服从均值为0,方差为σ2e的正态分布eit~N(0,σ2e)。
然而,现阶段中国股票市场还不够成熟,很多机构投资者也会捕捉某些明确的市场走势,顺势而为,采取趋势追随策略以获取短期收益。据此,我们认为机构投资者有时也会根据市场走势通过追随趋势预测价格,具体形式如式(2)所示。


既然机构投资者在获取上市公司的价值信息和分析市场的价格趋势上都有能力与优势,那么具体到每日交易,机构投资者选择哪种方式来形成价格预测呢?一个最直观的假设是看哪种预测方式给出的信号最为强烈或在近期表现得最好。具体地,采取式(4)的形式。

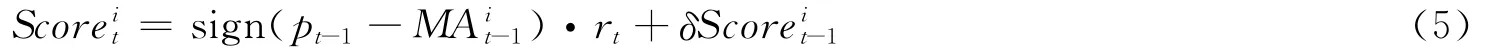
第2类是趋势交易者。他们无法获得较为准确的上市公司的价值信息(或成本太大),只能通过技术分析的手段依据近期价格趋势推测未来价格,其具体形式如式(6)。
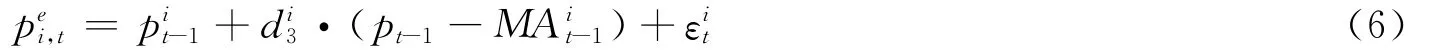
第3类是噪声交易者,他们为了满足自身流动性或风险对冲的需求进入市场,并不通过股票市场信息来盈利,其对价格的预测由当日的开盘价(前一日的收盘价)加上一个正态分布的随机噪声构成。

1.2.2.2 投资者的申购行为
各类投资者根据自身的资源禀赋及信息处理能力形成价格预测后,便进入市场参与交易。由于目前中国证券交易主要由限价订单构成,所以本文只考虑限价订单,由报价和报量两部分构成。
对于报价,当投资者预测价格将会上涨(下跌)时,结合自己的预测及下单前观测到的市场即时信息来进行买入(卖出)报价,买报价的具体形式分别见式(8),(9)。

对于报量,投资者会根据自身的风险偏好程度αi与当前可利用的财富(不考虑买空卖空)来确定。这里采用最简洁直接的形式——买卖报量与投资者的风险偏好及财富成正比,即买入报量卖出报量分别为投资者在上一期(当前可用)的现金财富与股票财富。
1.3 价格形成——连续双向拍卖机制
各类投资者按随机顺序进入市场下单,基于连续双向拍卖的基本机制,采用上海证券交易所的规则来确定双方的成交价格。具体地,进入市场的订单按价格优先和时间优先的准则在订单簿中排序,最优买入申报价格为最高买入申报价格,记为B*;最优卖出申报价格为最低卖出申报价格,记为A*。若新进入的买单报价则以A*的价格成交,即qτ=A*;若新进入的卖单报价,则以B*的价格成交,即qτ=B*。若最优买入申报价格与最优卖出申报价格相同,即A*=B*,则成交价格qτ=A*=B*。
当所有投资者都陆续进入市场参与完一次申购后,一个交易日结束。各类投资者根据各自的成交情况对自身的现金财富和股票财富进行清算,见式(10)。
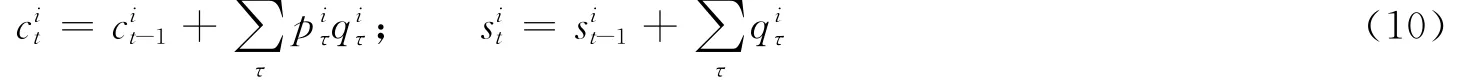
2 模拟结果分析
基于上述模型框架,本文进行了不同初值与参数组合的大量实验,以下展示的是一组具有代表性的模拟结果。对于模型的初始状态,设定市场中一共有(N=)500名投资者(在确保市场交易活跃的前提下,投资者数量初值的设定不影响以下模拟结果。例如,在以下基础实验的参数设置下,将N从500以500为间距增加至3 000,每组参数下运行20次取其均值,得到不同N值下系统稳态时对应的帕累托指数的均值为1.359,方差为0.002 6;基尼系数的均值为0.532,方差为0.000 3)。每位投资者均持有10 000元的现金和(等价的)100股的股票。股票的初始价值和价格均为100元。由于投资者在形成价格预测时涉及移动均线的时间窗口问题,股票价格的前100期设定为服从类似于其价值的几何随机游走过程,即ln(pt)=ln(pt-1)+ξt(ξt~N(0,0.52))。另外,考虑到不同类型的投资者具有不同的信息资源禀赋及信息处理能力(特别是机构投资者在信息资源禀赋和处理能力上占优),这会直接影响他在市场中的获利能力,对本文所关注的投资者整体财富分布和演化具有重要意义。所以在接下来的分析中,将机构投资者的初始市场占比作为一个关键变量(在确保交易活跃的前提下,其他类型投资者的初始占比对本文的基本结论没有定性影响)。据上证所[35]与深交所[36]的统计,从交易金额来看,目前中国机构投资者的市场占比约为15%。不失一般性地,以机构投资者的初始市场占比为15%,趋势交易者(包含趋势追随者和趋势反转者)以及噪声交易者各占剩余比例的1/3(即28.33%)为基础实验,并同时对不同市场占比(机构投资者市场占比从10%开始取值,以5%为步长,一直取到90%;个体投资者的3种类型各占剩余比例的1/3)对财富分布和演化的影响进行了探讨。模型的其它参数设置如表1所示。基于以上的初值及参数设定,每次模拟运行了5 000期,去除前500期暂态,用剩余的4 500期进行结果分析。同时,考虑到随机因素的影响,对于每组参数均模拟了20次以确保结果的稳定性。

表1 模拟结果的基本参数设置Tab.1 The basic parameters setting of the simulation
2.1 市场典型事实
图1、图2分别展示了市场中异质投资者间活跃的交易量及价格围绕价值上下波动的时间序列图。而图3、图4则分别展示了市场(对数)收益率与正态分布相比较的尖峰胖尾特性以及收益率时间序列的波动聚集特性,即大(小)的价格变动往往与大(小)的价格变动相连接。这一特性在收益率的绝对值序列上表现为逐渐衰减的显著的序列相关性(如图5所示)。相对应地,收益率本身却没有显著的序列相关性(如图6所示)。以上特性均与真实股票市场的主要典型事实[37]相吻合,说明本文的模型抓住了真实股票市场的关键机制与特性。
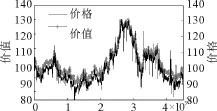
图1 股票价格与价值时间序列图Fig.1 The time series of stock prices with its fundamental values

图2 市场交易量时间序列图Fig.2 The time series of trading volume
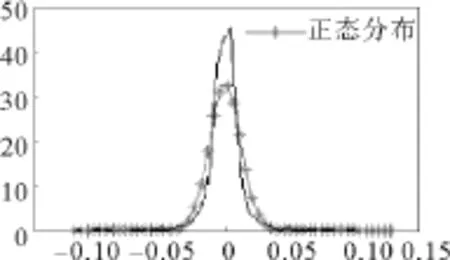
图3 市场对数收益率分布图Fig.3 The distribution of market log returns
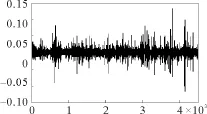
图4 市场对数收益率时间序列图Fig.4 The time series of market log returns
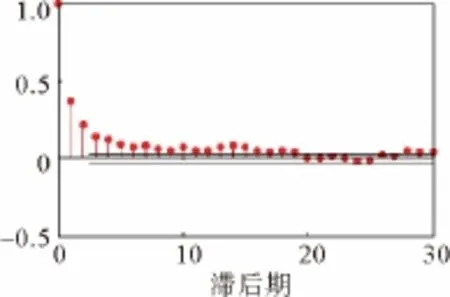
图5 市场对数收益率的绝对值的自相关系数图Fig.5 The autocorrelations of the absolute values of market log returns

图6 市场对数收益率的自相关系数图Fig.6 The autocorrelations of the raw values
当改变机构投资者的初始市场占比时,发现以上与真实市场相吻合的典型事实特性在较大参数范围内依然存在。同时,我们注意到,机构投资者的占比决定了其将股票价格拉回到真实价值附近的能力,对价格在某些时段偏离价值的幅度与持续期起着决定性的影响;并且,当机构投资者的占比较大时,市场对数收益率在较短滞后期内会表现出微弱的自相关性。
2.2 财富分布演化分析
2.2.1 总体财富分布的演化
图7a展示了市场中所有投资者财富的累积分布随时间的演化过程(由于最富有的5%投资者的财富与其余投资者的财富差距过大,为了避免“国王效应”[29],在该部分的分析中将其剔除)。在对投资者财富及其累积概率均取双对数坐标后,可以明显观察到财富分布的尾部(即图形的上半部分)可以近似用直线来拟合。并且随着交易的进行(从右向左),该直线变得更加陡峭,其斜率(等价于帕累托指数的倒数)越来越大。这意味着随着交易的进行,财富逐渐汇集到少数投资者手中,帕累托指数减小,与之对应的整体财富分布的基尼系数增大(见图7b),财富分布的非均等性增强。图8a展示了双对数坐标下终期(模型趋于稳态)投资者财富的累积分布,对其尾部10%的点做线性拟合,得到帕累托指数约为1.345,拟合优度R2为87.4%,p值为0.012(<5%)。图8b为对应的终期投资者财富分布的洛伦兹曲线,由此测算的基尼系数为0.553。经过同组参数下的20次实验,发现帕累托指数与基尼系数的大小受随机因素的影响较小,并且基尼系数相对于帕累托指数表现得更加稳定。具体地,帕累托指数的均值为1.42(相应拟合优度R2的均值为93.31%,p值的均值为0.006 4),中位数为1.30,方差为0.3;基尼系数的均值为0.534,中位数为0.533,方差为0.003 8。
当改变各类投资者的初始市场占比时,发现财富累积分布的尾部幂律特性保持不变。然而,随着机构投资者初始市场占比的增加,尾部帕累托指数先逐渐增大后趋于减弱(这是因为为了避免国王效应,在此计算的是尾部85%-95%的投资者的财富帕累托指数,若将最富有5%的投资者的财富包含进来,其帕累托指数是一直增大的);对应的基尼系数单调递减,意味着整体市场财富分布的非均等程度减小,如图6所示。可见初始资源禀赋的配置对终期财富分布及其演化起着决定性的作用。增加机构投资者的比重,意味着初始时刻享有优势资源的投资者数量增加,初始资源禀赋的非均等程度减小,从而终期财富分布的非均等程度也随之缩小。
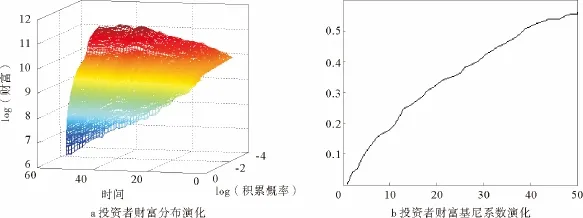
图7 投资者财富累积分布及对应的基尼系数随时间的演化图Fig.7 The evolutions of the cumulative distribution of investors′wealth(a)with the corresponding Gini coefficients(b)
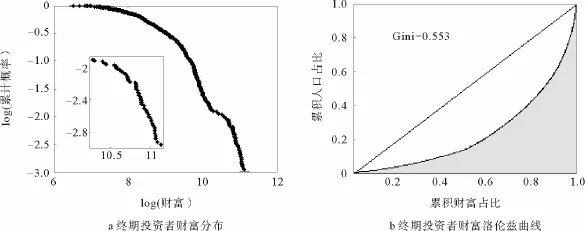
图8 终期投资者财富累积分布图(a)及财富洛伦兹曲线(b)Fig.8 The finial cumulative distribution of investors′wealth(a)and its corresponding Lorenz curve(b)
2.2.2 各类投资者财富变化情况分析
图10展示了各类投资者的财富占比随时间的演化,明显可以看出拥有信息资源及信息处理优势的机构投资者的财富占比整体呈现出上升趋势,而趋势投资者与噪声交易者的财富占比则整体呈现下降趋势。最终,3类投资者的占比趋于稳定。这印证了投资者总体财富尾部呈现出的幂律分布源于收益向资源占优的机构投资者手中的转移与积累。在基础实验的初值与参数设置下,进行了20次实验所得到的各类投资者终期的财富占比相关统计量如表2所示。从中可以看出,机构投资者的财富占比从初始的15%上升至50.43%,其余各类投资者的占比均有下降。同时,各类投资者终期财富占比的大小基本不受模型中随机因素的影响,实验的方差都很小。

图9 机构投资者初始占比与终期投资者财富分布的对应关系Fig.9 The corresponding relationship between the initial share of institutional investors and the equity of the finial wealth distribution

表2 基础实验各类投资者终期财富占比统计特征Tab.2 The statistics of the finial wealth shares of different types of investors in the basic experiment
当增加机构投资者的初始市场占比时,发现尽管财富仍然向具有资源优势的机构投资者手中聚敛,但聚敛的速度在不断下降,机构投资者财富的增加变得缓慢。表3展示的是各类投资者终期的人均财富相对于其初始财富W0的比例。从中可以明显看出,随着机构投资者初始市场占比的增加,其终期人均财富相对于初始财富W0的积累倍数在逐渐递减。这是由于伴随着机构投资者初期市场占比的增加,其余投资者占比减少,机构投资者凭借信息资源及处理能力的优势能够实现从其他投资者向自身的财富转移减少,从而使整体财富分布的基尼系数减小,财富分布的非均等程度有所减缓。
3 结论与探讨
本文通过对市场中各类投资者投资行为的刻画,自下而上地构建了能够展现真实股票市场特性(如收益率尖峰胖尾、波动聚集等)的人工股票市场,同时发现随着交易的进行,市场整体财富分布从最初的均匀分布演变为尾部的幂律分布,整体财富分布的基尼系数逐渐增大,意味着投资者财富分布从均等向非均等的演变。这源于市场收益从一般投资者向具有信息资源获取及处理优势的机构投资者手中的转移与积累。而财富分布的非均等程度会随着该初始禀赋及能力更加均等(实验中表现为机构投资者初始市场占比的增加)而减弱。
当然,由于本文着重强调机构投资者在信息资源的获取和处理上与大多数个体投资者相比具有绝对优势,所以在模型设计上采取了一个较为理想化的假设,即所有机构投资者都能够一致地较为准确地获取上市公司股票的基本价值。基于该假设,当机构投资者的交易占比达到市场的真实比例时(如中国目前的15%左右),其对市场价格的影响力终究能够较为及时地将价格拉回价值附近,避免价格对价值的持续偏离,也使得机构投资者从价格向价值的回复过程中获取收益。当然机构投资者交易占比越少,其对市场价格的影响力越小,将价格拉回价值时所需要的时间就越多。而当机构投资者交易占比非常少时(如低于10%),价格长期偏离价值而不能回复的极端情形开始间或出现。在此情形下,机构投资者并未表现出绝对优势,反而是趋势反转与趋势追随占优,整体市场的财富分布也会较为平均。由于此种情形不论在真实市场中还是在模型中都较少出现,所以本文并未对其展开具体讨论。
同时,为了与机构投资者在信息获取和处理能力上的绝对优势形成清晰的对比,模型在对个体投资者的刻画上,除了假设他由于不能准确获取上市公司的基本价值(或成本太高)而无法采取价值投资策略外,对于基本的趋势追随和趋势反转策略,个体投资者也是从一而终,并未考虑其测算收益后可能发生的策略更新行为。这样的处理方式一是为了避免模型参数过多而增添额外的复杂性,二是考虑到目前关于投资者策略更新方式的实证研究比较有限,很多问题也存在争论,如采取什么样的函数进行收益的测算,采用什么样的频率进行更新等等。

图10 不同类型投资者的财富占比演化图Fig.10 The evolutions of the wealth shares of different types of investors
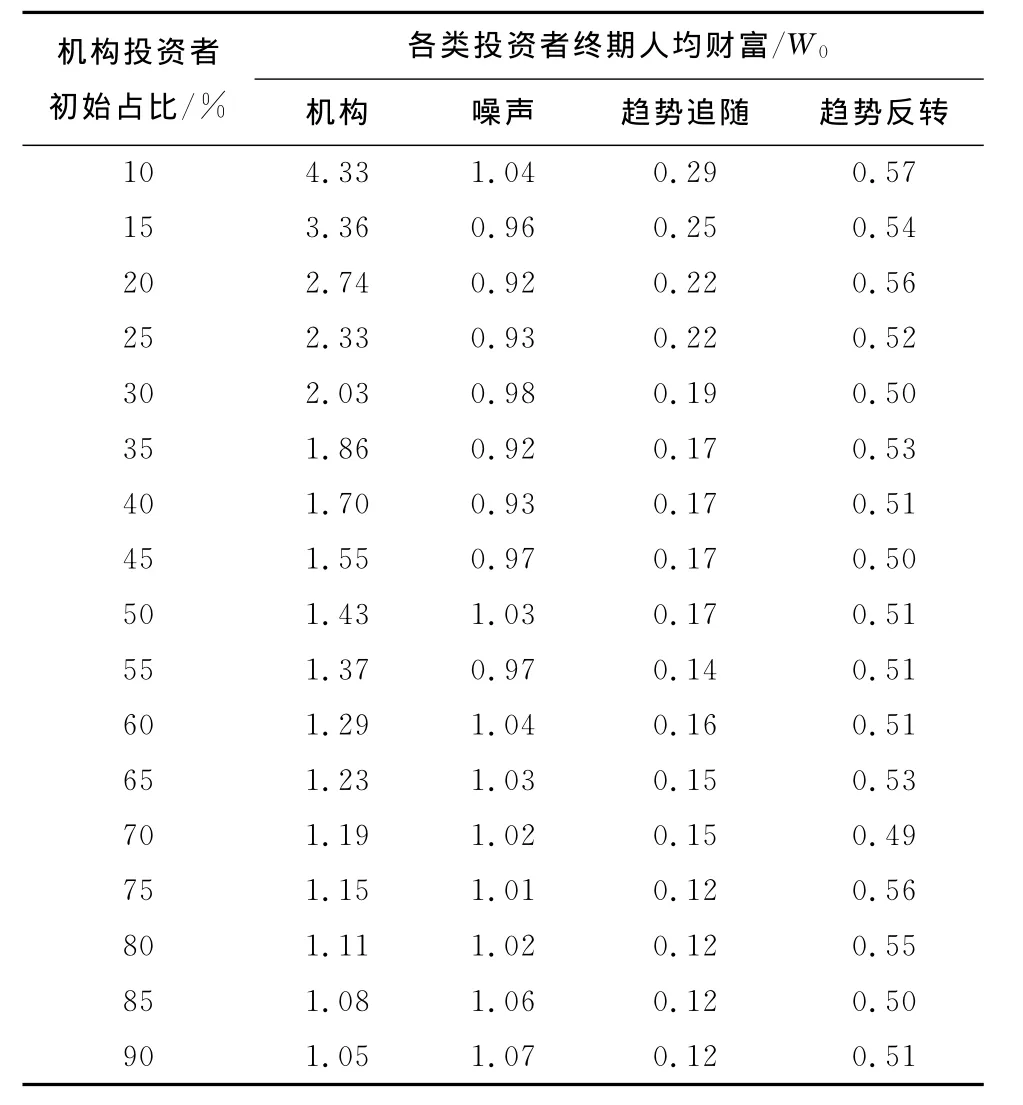
表3 机构投资者初始占比与各类投资者终期人均财富的对应Tab.3 The finial wealth per capital of different types of investors as the initial share of institutional investors increasing
当然,加入个体投资者的策略更新会使得本文的模型更贴近实际。对此,在原有模型设置的基础上,我们初步尝试了加入目前常用的一种更新方式来刻画个体投资者的策略更新行为,即当个体投资者采用的原有策略产生损失时,他会以一定的概率转移到其他策略,该转移概率的大小与趋势追随和趋势反转两类策略之前的累积收益成正比(为了保证市场的成交量,噪声交易主要来自于流动性或风险对冲等便利性需求,不参与策略的更新)。具体形式为
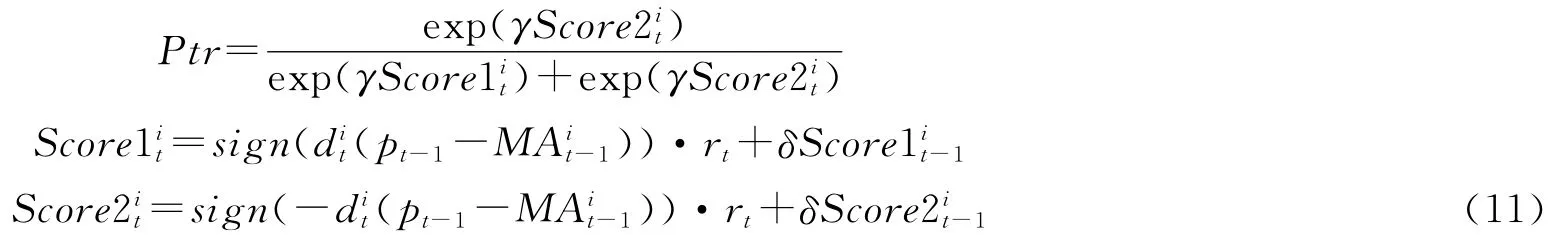
其中,Score1与Score2分别记录个体投资者当前采用的策略及其相反策略的累积得分。γ>0为策略转移强度,γ越大,由于两种策略得分差异而产生的向另一种策略转移的概率就越大。当个体投资者所采用的当前策略的累积得分Score1低于0时,即投资者在一段时间的累积收益为负时,他将以概率Ptr转移至相反的策略,即其趋势追随或反转程度也就是如果之前是趋势追随,那么转移后便是趋势反转。反之亦然。
基于此,我们所得到的基本结论与本文之前的结论一致,即增加机构投资者的占比会使整体市场财富分布的非均等性得以改善。有所区别的是,在同样的参数设置下,加入个体投资者的策略更新行为反而会使得市场终期财富的非均等程度增加,即基尼系数增大。分析其原因,我们认为个体投资者由于不具有准确获取上市公司股票基本价值的途径或能力,他们的策略转换只能在产生损失时以一定的概率转换到另一种策略。而这样的转换方式,会使得个体投资者向前期获利的策略聚集,但前期获利的策略不一定在后期表现良好,并且这样类似于羊群效应的聚集行为反而会使个体投资者购入股票的成本偏高,出售股票的价格偏低,从而加大其获得损失的可能性,表现为趋势追随与趋势反转两类交易者的占比交替地呈螺旋式更快地衰减。当然,该演化特性与个体投资者的策略更新方式密切相关。在更复杂的策略更新方式下,如采用类似生物学中的遗传、突变与自然选择的过程在淘汰已有策略的同时,产生新的策略,增强市场的策略多样性,可能会得到不一样的价格和财富演化。
另外,本文模型所描述的市场环境相对封闭,即市场中的投资者数目固定,现金财富只是在股票市场的不同投资者间流动,而不涉及新旧投资者的进入和退出以及股票市场之外的现金的流入和流出。市场的开放程度对于价格和财富的演化也会有一定影响。考虑更贴近真实市场的策略更新方式以及更加开放的市场环境将是本文工作进一步改进和完善的主要方向。
4 建议
近年来,中国证监会从降低股市风险、增进市场效率的目标出发一直呼吁推动资本市场的结构调整,积极采取各项措施以增加机构投资者的比重,如逐步放开境外机构投资者QFII进入并增加其投资额度,鼓励社保基金、企业年金、保险公司等机构投资者增加其对资本市场的投资比重,积极推动全国养老保险基金、住房公积金等长期资金入市[38]等等。而本文的研究表明,机构投资者比重的增加,对于促进股市财富配置的公平性也有显著的作用。所以我们要将各项增加机构投资者比重的措施积极地开展下去。同时,创造多样化的投资理财渠道,合理引导个人投资者通过投资于机构来间接地受惠于股票市场。
另外,从信息资源更加均等的角度出发,增加上市公司的信息披露,使体现公司价值的信息的可获取性增加,同时保证信息的准确性,加强信息披露的监管与处罚,为上市公司的信息披露建立诚信档案,能够改善股市财富配置的非均等程度。
最后,由于中国股市中个人投资者仍占较大比重,其信息处理能力有限,交易频繁,持股期限短,亏损比例较为严重,是股市生态中的薄弱环节[33]。所以从信息处理能力更加均等的角度出发,推广股市投资知识与技能的大众化宣传与培训,增进个人投资者对市场风险的认识,能够改善股市财富配置的非均等程度。
[1] Farmer J D,Foley D.The economy needs agent-based modeling[J].Nature,2009,460:685-686.
[2] Buchanan M.Meltdown modeling:could agent-based computer models prevent another financial crisis?[J].Nature,2009,460:680-682.
[3] 李红权.计算金融学与政策模拟的前沿动态[J].计算机工程与应用,2010,46(18):21-23.Li Hongquan,Agent-based computational finance and policy simulation in financial markets:review and comment[J].Computer Engineering and Applications,2010,46(18):21-23.
[4] 张维,冯绪,熊熊,等.计算实验金融在中国:研究现状及未来发展[J].系统管理学报,2012,21(6):756-764.Zhang Wei,Feng Xu,Xiong Xiong,et al.Agent-based computational finance in China:its present state and future prospects[J].Journal of Systems & Management,2012,21(6):756-764.
[5] 范如国,叶菁,杜靖文.基于 Agent的计算经济学发展前沿:文献综述[J].经济评论,2013,(2):145-150.Fan Ruguo,Ye Jing,Du Jingwen.Frontier development of agent-based computational economics:a survey[J].Economic Review,2013,(2):145-150.
[6] LeBaron B.Agent-based financial markets:matching stylized facts with style[C]//Colander D.Post Walrasian Macroeconomics:Beyond the DSGE Model.Cambridge:Cambridge University Press,2006:221-238.
[7] Smith V L.An experimental study of competitive market behavior[J].The Journal of Political Economy,1962,70(2):111-137.
[8] Chan N T,LeBaron B,Lo A W,et al.Agent-based models of financial markets:a comparison with experimental markets[EB/OL].[2013-08-30].http://dx.doi.org/10.2139/ssrn.290140.
[9] Gode D K,Sunder S.Allocative efficiency of markets with zero intelligence(ZI)traders:market as a partial substitute for individual rationality[J].Journal of Political Economy,1993,101:119-137.
[10]Zhan W,Zhang J,Yang J,et al.K-ZI:ageneral zero-intelligence model in continuous double auction[J].International Journal of Information Technology & Decision Making,2002,1(4):673-691.
[11]詹文杰,占俊英.连续双向拍卖中的 “增强零信息”策略研究[J].管理评论,2008,20(5):44-50.Zhan Wenjie,Zhan Junying.Study of zero-intelligence plus trading strategies in continuous double auction market[J].Management Review,2008,20(5):44-50.
[12]LiCalzi M,Pellizzari P.The allocative effectiveness of market protocols under intelligent trading[C]//Bruun C.Advances in Artificial Economics.Berlin:Springer,2006:17-29.
[13]Rust J,Palmer R,Miller J H.Behavior of trading automata in a computerized double auction market[EB/OL].[2013-08-30].http://www.santafe.edu/media/workingpapers/92-02-008.pdf.
[14]詹文杰,邵原.连续竞价市场的交易策略研究综述[J].管理学报,2008,5(6):921-927.Zhan Wejie,Shao Yuan.Review on trading strategy of continuous double auction[J].Chinese Journal of Management,2008,5(6):921-927.
[15]赵志刚.学习模型与资产市场[D].天津:天津大学管理学院,2010.Zhao Zhigang.Learning models and asset market dynamics-a research of agent-based computational finance[D].Tianjin:School of Management,Tianjin University,2010.
[16]宋逢明,李超.股票市场涨跌停板设置的微模拟研究[J].运筹与管理,2007,16(1):100-106.Song Fengming,Li Chao.Microscopic simulation research into the ideal price limit on stock market[J].Operations Research and Management Science,2007,16(1):100-106.
[17]巩兰杰,王春峰,房振明.基于 Agent的连续双向拍卖人工股市建模研究[J].计算机应用研究,2008,25(12):3602-3604.Gong Lanjie,Wang Chunfeng,Fang Zhenming.Research on modeling of agent-based artificial stock market with continuous double auction mechanism [J].Application Research of Computers,2008,25(12):3602-3604.
[18]Mike S,Farmer J D.An empirical behavioral model of liquidity and volatility[J].Journal of Economic Dynamics &Control,2008,32:200-234.
[19]陈莹,袁建辉,李心丹,等.基于计算实验的协同羊群行为与市场波动研究[J].管理科学学报,2010,13(9):119-128.Chen Ying,Yuan Jianhui,Li Xindan,et al.Research on collaborative herding behavior and market volatility:based on computational experiments[J].Journal of Management in China,2010,13(9):119-128.
[20]马正欣,张维,熊熊,等.指令簿透明度增加与市场价格发现——基于计算实验金融方法的指令驱动市场研究[J].南开经济研究,2011,(1):132-141.Ma Zhengxin,Zhang Wei,Xiong Xiong,et al.Increasing order book disclosure will promote price discovery?——a research in order-driven market based on agent-based computational finance[J].Nankai Economic Studies,2011,(1):132-141.
[21]Anufriev M,Valentyn P,Jasmina A,et al.Efficiency of continuous double auctions under individual evolutionary learning with full or limited information[J].Journal of Evolutionary Economics,2013,23(3):539-573.
[22]Li Y L,Zhang W,Zhang Y J,Zhang X T,Xiong X.Calibration of the agent-based continuous double auction stock market by scaling analysis[J].Information Science,2014,256:46-56.
[23]李悦雷,张维.基于计算实验金融的连续双向拍卖股票市场交易机制研究[D].天津:天津大学管理学院,2012.Li Yuelei,Zhang Wei.The investigation of trading mechanisms in continuous double auction stock market based on agent-based computational finance[D].Tianjin:School of Management,Tianjin University,2012.
[24]李悦雷,张维,熊熊.最小报价单位对市场流动性影响的计算实验研究[J].管理科学,2012,1:92-98.Li Yuelei,Zhang Wei,Xiong Xiong.Impact of tick size on market liquidity by agent-based modeling approach[J].Journal of Management Science,2012,1:92-98.
[25]Pareto V.Cours d′economie Politique[M].Lausanne and Paris:Rouge and Cie,1897.
[26]Arnab C,Sitabhra S,Bikas K C.Economic inequality:is it natural?[J].Current Science,2007,92(10):1383-1389.
[27]Levy M,Solomon S.New evidence for the power-law distribution of wealth[J].Physica A,1997,242(1/2):90-94.
[28]Adrian D,Victor M Y.exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States[J].Physica A,2001,299(1/2):213-221.
[29]Sinha S.Evidence for power-law tail of the wealth distribution in India[J].Physica A,2006,359:555-562.
[30]高建敏,王炳兴.中国财富分布规律的实证研究[J].浙江工商大学学报,2007,(1):61-65.Gao Jianmin,Wang Bingxing.An empirical research on the distribution of wealth in China[J].Journal of Zhejiang Gongshang University,2007,(1):61-65.
[31]Persky J.Retrospectives:Pareto′s law [J].Journal of Economic Perspectives,1992,6(2):181-192.
[32]Gini C.Measurement of inequality and incomes[J].Economic Journal,1921,31,124-126.
[33]Newman M E J.Power laws,Pareto distributions and Zipf′s law [J].Contemporary Physics,2005,46(5):323-351.
[34]Dalton H.The measurement of the inequality of incomes[J].Economic Journal,1920,30:348-361.
[35]上交所.上交所统计年鉴(2012年卷)[DB/OL].[2013-08-30].http://www.sse.com.cn/researchpublications/publication/yearly/c/tjnj_2012.pdf.Shanghai Stock Exchange.Shanghai stock exchange statistics annual(2012)[DB/OL].[2013-08-30].http://www.sse.com.cn/researchpublications/publication/yearly/c/tjnj_2012.pdf.
[36]深交所.从近年数据看深市投资者结构和行为变化特征[DB/OL].[2013-05-08].http://www.szse.cn/main/aboutus/bsyw/39749823.shtml.Shenzhen stock exchange.The properties of the changes in investor construction and behaviors——the evidences from the market data of recent years[DB/OL].[2013-05-08].http://www.szse.cn/main/aboutus/bsyw/39749823.shtml.
[37]Cont R.Empirical properties of asset returns:stylized facts and statistic issues[J].Quantitative Finance,2001,1(2):223-236.
[38]郭树清,增加机构投资者比重 鼓励养老金入市[DB/OL].[2012-02-02].http://finance.sina.com.cn/stock/t/20120202/011911293079.shtml.Guo Shuqing,Increasing the proportion of institutional investors and encouraging the pensions to invest in the stock markets[DB/OL].[2012-02-02].http://finance.sina.com.cn/stock/t/20120202/011911293079.shtml.

