Dynamic parameters identification withconsidering hyper-viscoelasticof rubber bushing

Gang LEI1，2*，Ying LIU1，Peng HU2，Qian CHEN1（1Key Laboratory of Advanced Manufacturing Technology for Automobile Parts，Ministry of Education，Chongqing University of Technology，Chongqing 400054，China）（2Chongqing Research Center for Rall Transit&Automobile parts，Chongqing Academy of Science and Technology，Chongqing 400054，China）

Dynamic parameters identification with
considering hyper-viscoelastic
of rubber bushing

Gang LEI1，2*，Ying LIU1，Peng HU2，Qian CHEN1（1Key Laboratory of Advanced Manufacturing Technology for Automobile Parts，Ministry of Education，
Chongqing University of Technology，Chongqing 400054，China）（2Chongqing Resea
rch Center for Rall Transit&Automobile parts，Chongqing Academy of Science and Technology，Chongqing 400054，China）

The rubber bushing of the macphersan suspension control arm is researched in this paper.Based on a hyper-viscoelastic constitutive model of rubber bushing，the finite element model is established and the results of simulation are compared with experimental data.By the FE software，high precision mechanical parameters based on the viscoelastic constitutive model in frequency domain of rubber are identified from dynamic characteristic test data.The dynamic characteristic hysteresis loops of the rubber bushing are acquired in the nonlinear FE software，and the information of damping angles is also obtained.Then the complete dynamic parameters are identified.

Rubber bushing，Hyper-viscoelastic constitutive model，Dynamic parameters identified

Hydromechatronics Engineering

http：//jdy.qks.cqut.edu.cn

E-mail：jdygcyw@126.com

With the rapid development of the auto industry，people express higher requirements about the performance of the car，especially the ride comfort.Nevertheless，the vibration and noise of the car affects the ride comfort directly，and there is a variety of complicated reasons contribute to the vibration，with the excitation of uneven road and engine torque is the most significant.As a key component，suspension transfers the road excitation to auto body and the performance of suspension seriously affects the comfort of the vehicle.

The multitudinous studies of the suspensions concentrated on guide mechanisms，positional parameters，springs and damping element，etc.At currently，as a buffer element of the suspensions，the rubber bushing has not been universally studied.Based on reducing vibration and noise as well as compensating for manufacturing tolerance，the rubber bushing have a great influence on the NVH characteristics of the car.With nonlinear in material properties，the mechanical properties of the rubber-like materials present more complex.The impact of the external factors，such as temperature，preload，loading speed，on the characteristics of the rubber-like materials is also obvious［1］.Because of the study on the rubber-like material has not yet been a complete theoretical system of mechanics，determining the parameters of rubber material and analyzing the characteristics of dynamic and static has been a difficult problem.Obtaining material parameters of the rubber with material basic experiment due to the shortage of necessary experimental appliances is not widely used.Based on the simulation of the nonlinear FE software，the dynamic and static characteristics of the rubber can be achieved.

In this paper，based on the hyper-viscoelastic constitutive model of rubber and FE optimization technique，high precision viscoelastic mechanical parameters in frequency domain of rubber were identified without the experimental date of material creep and stress relaxation.Meanwhile，the complete dynamic characteristics information can be reconstructed.

1 Hyper-viscoelastic constitutive mode

The dynamic characteristics of rubber bushing are affected by the excitation frequency and amplitude. The excitation of frequency and amplitude can be determined by the viscoelasticity and the friction characteristics of rubber material respectively［2-3］.

This paper studied on an axisymmetric rubber bushing of the McPherson front-suspension control arm，as shown in Fig.1.

Fig.1 ReaI modeI of rubber bushing

Based on considering the dynamic characteristic influence of the excitation frequency and neglecting rubber friction characteristics namely the excitation amplitude，this study used three-order Ogden constitutive model of hyperelastic model，with six coefficients，to describe the elastic characteristics of rubber material. The dynamic characteristics of rubber is described by the viscoelasticity three-order prony series constitutive equation which determined by generalized Maxwell constitutive model.

1.1 Three-order ogden constitutive hyperelastic model

Based on the theory of continuum mechanics，the Ogden constitutive model is one of the best functions that fit the silicone-rubber experimental date especially the large deformation test.The constitutive equation of the Ogden，with the main elongation λ1，λ2，λ3as the variable，takes the form：

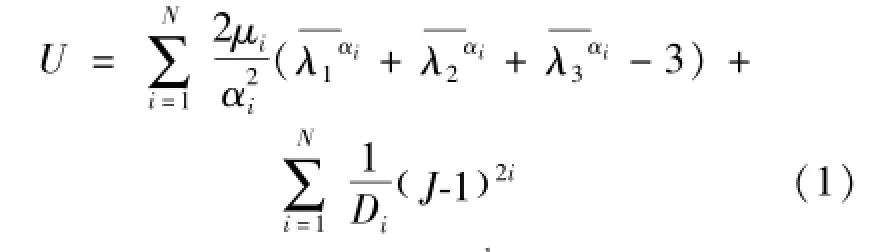
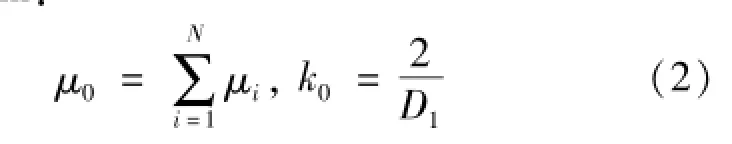
In this paper，the hyperelastic characteristic of the rubber bushing is described by the three-order（N= 3）Ogden constitutive model.

1.2 The prony series viscoelasticity equation of generalized Maxwell model

Generalized Maxwell model is constituted by multiple parallel Maxwell elements.The modulus，viscosity and slack time of sub-model can be different.In Fig. 2，the G and η are spring elasticity coefficient and viscous damping coefficient respectively.

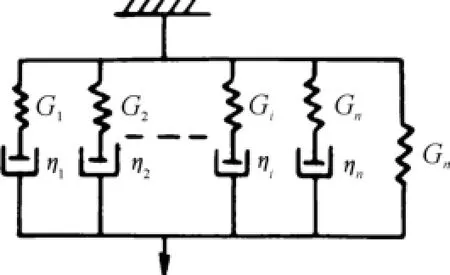
Fig.2 GeneraIized MaxweII modeI

Composite modulus G*of the generalized Maxwell model is expressed as：

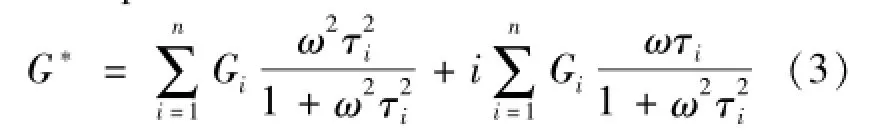
Supposing，the loss modulus of first element in generalized Maxwell is 0.The storage modulus of the first element is tantamount to G1namely elastic coefficient. Then the prony series equation is obtained.

The storage modulus is described：

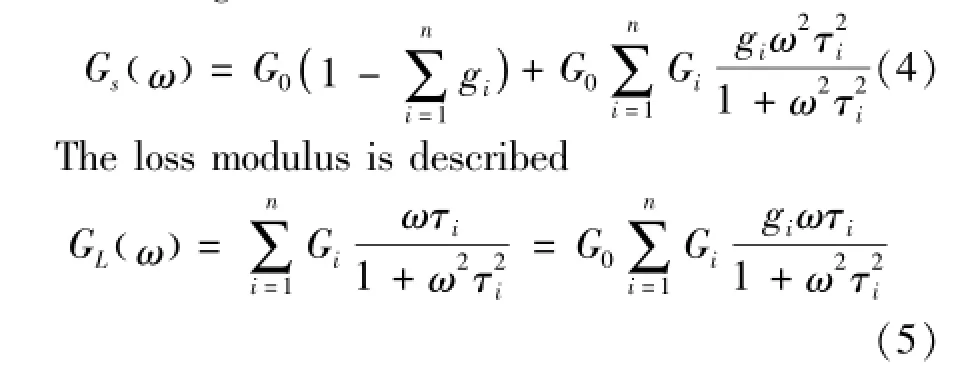
Where ω is pi and τ is shear stress.

2 The dynamic characteristics experiment

The dynamic characteristics of the rubber bushing，based on constant amplitude，mainly mean the effect on the relationship between displacement and frequen-cy while dynamic load is applied.Dynamic stiffness and damping angles are the main evaluation parameters of the dynamic characteristics of the rubber bushing.The study on mechanical Properties of rubber bushing obtains the displacement and force of axial（Z）and radial（X，Y）with different frequency in the case of alternating load and then the dynamic stiffness and damping angle altering with frequency is defined［4］.

The bi-directional dynamic characteristics experiment of rubber bushing was done on MTS831 test-bed. The rubber bushing was installed on the clamp and simultaneously intermediate shaft was fixed.With increasing the frequency one by one from 0 to 25 Hz，an imposed displacement excitation namely Y（t）= Ysin（ωt）was applied on terminal of the test-bed.The signals of displacement X（t）and the reaction forces F（t）are recorded.The hysteretic curve of the dynamic characteristics is obtained and the complete dynamic characteristics of the rubber bushing can be defined based on the following formulas.

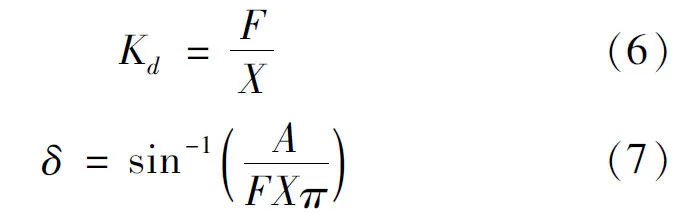
Among the formulas，the Kdis dynamic stiffness of the rubber bushing，F and X are the response of reaction forces and displacement respectively，δ is damping angle and A denotes the area of the return curve.

Two sets of data about the dynamic characteristic below are obtained from the test.

1）With the displacement excitation of axial was applied while the amplitudes of the excitation are 2mm，1.5mm，1mm and 0.52 mm respectively，the dynamic stiffness curves are obtained as shown in Fig.3.

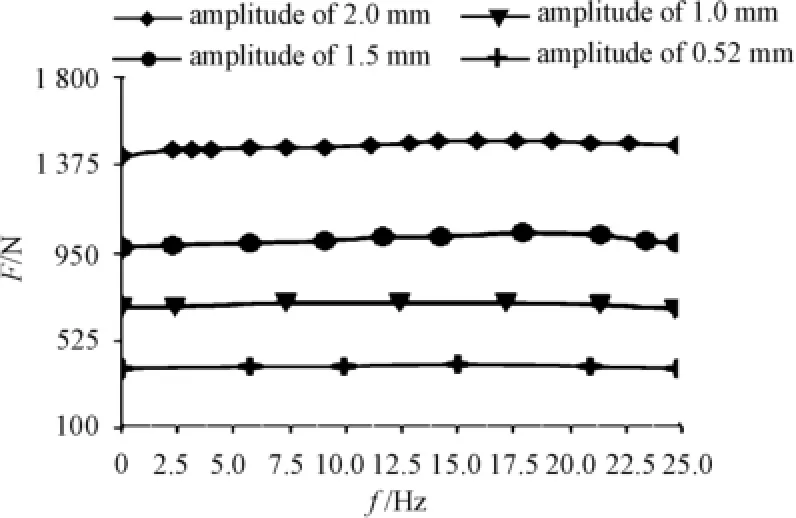
Fig.3 AxiaI dynamic stiffness curves（test）

2）With the displacement excitation of radial was applied while the amplitudes of the excitation are 1mm，0.7mm，0.51mm and 0.34mm respectively，the dynamic stiffness curves are obtained and as shown in Fig.4.

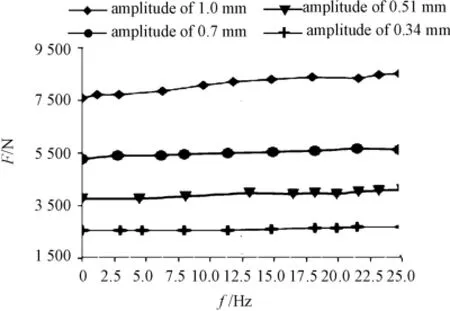
Fig.4 RadiaI dynamic stiffness curves（test）

3 The simulation for dynamic characteristics of rubber bushing

3.1 The simulation with the initial parameters

Mechanical characteristics of rubber filler is described with a hyper-viscoelastic constitutive model（superposition of hyperelastic and viscoelastic constitutive model）while the dynamic characteristics of the rubber bushing is analyzed by FE simulation.

The three-order Ogden constitutive model is utilized to define the hyperelastic property and the coefficients，which has been determined by parameter identification and can accurately express the static characteristics of the rubber bushing，is selected as the material constitutive.As shown in Table 1［5-6］.

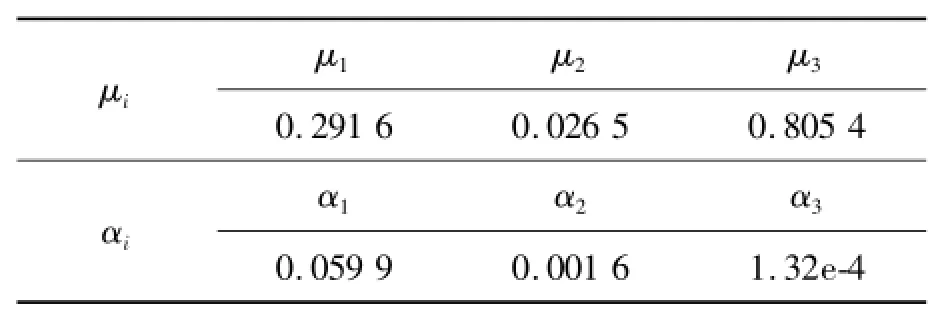
TabIe1 Three-order ogden constitutive parameters

The three-order prony series，determined by generalized Maxwell constitutive model，is used to express the viscoelastic property of the rubber bushing and the initial coefficients of simulation references dissertation［7］，as Table 2 revealed.

Based on the direct response algorithm of steadystate dynamics with harmonic excitation，the dynamic characteristics of rubber bushing is analyzed in nonlinear FE software（Abaqus）.The FE model shown in Fig.5.

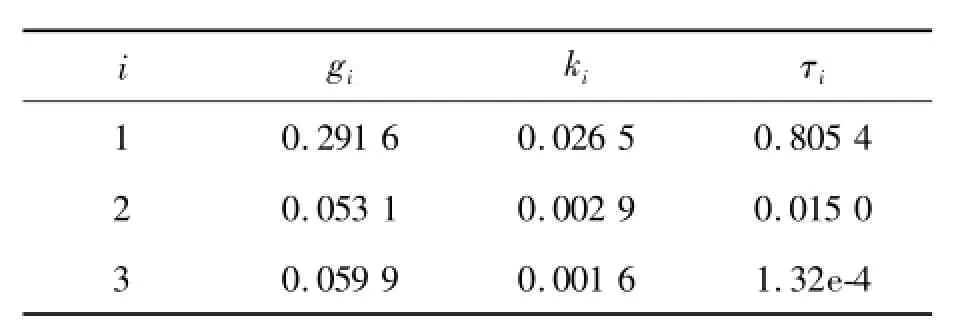
TabIe2 The coefficients of three-order prony series

Fig.5 The FE modeI of rubber bushing

According to the conditions of the dynamic experiment，the boundary conditions of rubber bushing for simulating are established，as shown in Table 3.

TabIe3 Boundary conditions of dynamic anaIysis

The results of simulation，with incentive amplitudes of 1.5mm in axial and 1mm in radial direction respectively，were compared with the test date shown in Fig.6 and 7.

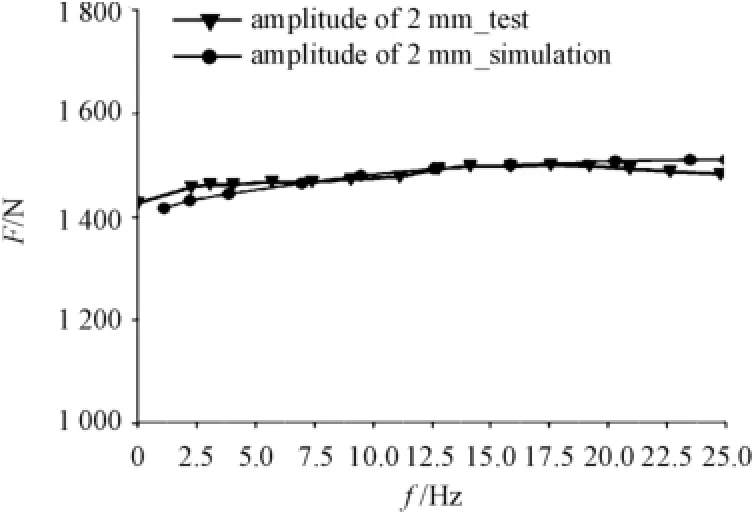
Fig.6 AxiaI initiaI dynamic stiffness curves

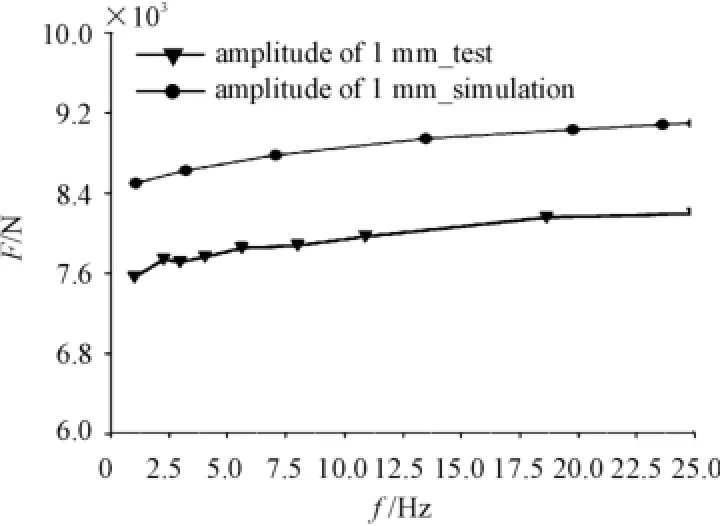
Fig.7 RadiaI initiaI dynamic stiffness curves

Comparatively，there is a considerable gap between the curves which represent the dynamic characteristics of rubber bushing extracted from the simulations and experiments，in particular the radial direction.Therefore，it’s apparent that the initial coefficients of threeorder prony series do not exactly match this rubber bushing.

3.2 Parameter identification of the hyper-viscoelastic constitutive model

By a parameter identification technology and the A-daptive Response Surface Method in nonlinear FE sofeware，the high precision mechanical parameters of the viscoelastic constitutive model in frequency domain of rubber based on the dynamic characteristic test date can be identified.When the simulated results present apparent deviation from the dates of the experiment，the coefficients of the viscoelastic constitutive model can be redefined until coinciding with each other.

3.2.1 Design variables and objects of optimization

The nine coefficients in the three-order prony series equation，accurately expressed the dynamic characteristics of the rubber bushing，are selected as the design variables.The initial coefficients shown in Table 2 and the lower and upper bounds of the values［8］were defined in Table 4.

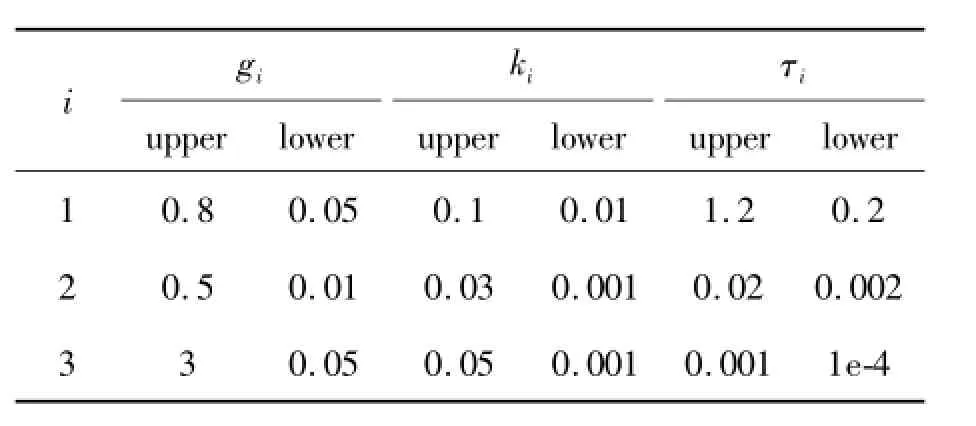
TabIe4 Lower and upper bounds of the design variabIes

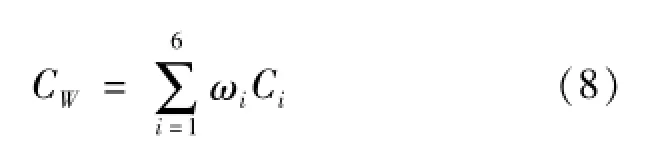
As the weighted sum，Cwis the general goal；ωiare weights in the optimization procedure and Ciare the functions of the sub-objectives.

3.2.2 Parameter indentification

According to reverse algorithm，the optimized coefficients of the material viscoelastic constitutive model are determined while the objective function reaches the minimum.This study found an optimum solution to describe the parameter of the material constitutive model in the viscoelastic mechanical behavior of the rubber bushing by the ARSM.The optimized coefficients of the material viscoelastic constitutive model are shown in Table 5.

The dynamic characteristics date of simulation，axial direction applied displacement excitation with constant amplitudes of 1.5 mm and radial direction applied displacement excitation with constant amplitudes of 1mm，were selected to establish the functions of optimized objects.Six sub-objectives are proposed as follows.

1）The area enclosed by the axial dynamic characteristics simulated curve and abscissa axial is introduced as a response for this sub-objective，while the corresponding value of experiment is applied as the target value.

2）The area enclosed by the radial dynamic characteristics simulated curve and abscissa axial is introduced as a response for this sub-objective，while the corresponding value of experiment is applied as the target value.

3）The initial point and endpoint value on axial dynamic characteristics simulated curve are expected to approximate the corresponding value of experiment.

4）The initial point and endpoint value on radial dynamic characteristics simulated curve are expected to approximate the corresponding value of experiment.

Since the experimental and simulated curves are linear ranging from the minimum to the maximum value of the frequency excitation applied in this study，the above six sub-objectives are able to make the simulated curves overlap the corresponding value of experiment and replicate the axial and radial dynamic characteristics experiment.

To integrate the six sub-objectives mentioned above into one general goal，the weighted equation is employed：

TabIe5 The optimized coefficients of materiaI

The hyper-viscoelastic constitutive model of rubber bushing，based on overlaying the three-order Prony series equation and three-order Ogden hyperelastic constitutive mode，is established and analyzed.The viscoelastic parameters in frequency domain are selected in accordance with the optimized coefficients of material.

The dynamic stiffness of the simulated versus experimental frequency-stress curvilinear relationship in axial and radial is shown in Fig 8，9 respectively.

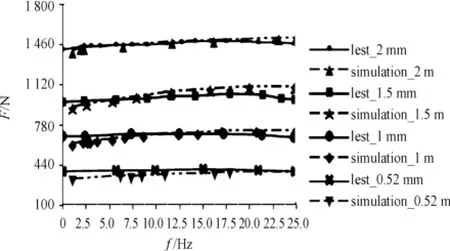
Fig.8 AxiaI dynamic stiffness curves（after optimization）

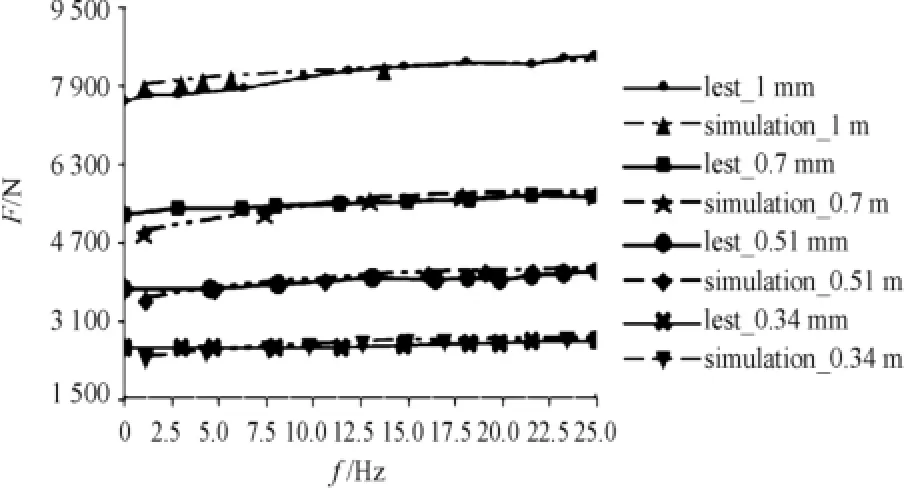
Fig.9 RadiaI dynamic stiffness curves（after optimization）

According to the dynamic stiffness results of comparison，the simulated results of rubber bushing in the axial are close to experiment.The deviation in radial is more obvious from 0 to 7.5 Hz.However，with increasing of the frequency，the deviation shrinks obviously and the simulated curve constantly approaches to the corresponding value of experiment.The simulated model based on parameters identification is more accurate for describing the dynamic characteristics of viscoelastic properties of the rubber bushing.

3.3 Restructuring of the dynamic characteristics information

As the evaluation index of the dynamic characteristics of the rubber bushing，the dynamic stiffness and damping angle are obtained through dynamic characteristic test in general.Without obtaining the information of damping due to the shortage of necessary experimental appliances，the dynamic stiffness is acquired while the harmonic excitation in radial and axial is applied in this paper.Through parameter identification technology，high precision parameters of the viscoelastic constitutive model of rubber were identified.Based on the finite element techniquethe，the dynamic characteristics of the bushings are analyzed further in order to reconstruct the complete dynamic characteristic information of the rubber.

The boundary Conditions for simulation are shown in Table 6.

TabIe6 The boundary Conditions for simuIation

The dynamic characteristic hysteresis loops of the rubber bushing in axial and radial are determined respectively as shown in Fig.10，11.

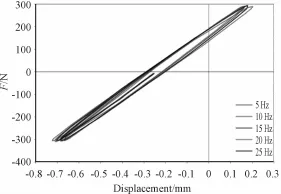
Fig.10 Hysteresis Ioops in axiaI excitation

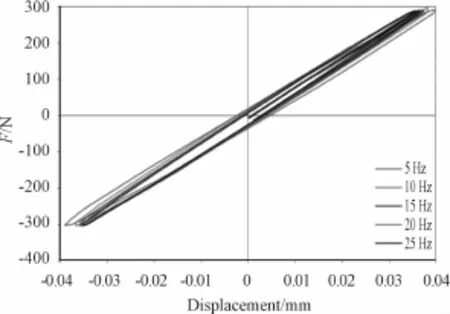
Fig.11 Hysteresis Ioops in radiaI excitation

Based on the simulated results which applied excitation in axial and radial，the information of damping angle can be calculated by formula（7）.The complete dynamic characteristics informationoftherubber bushing is obtained.

4 Conclusions

Based on the FE optimization technique，the high precision viscoelastic mechanical parameters in frequency domain of rubber were identified uniting the dynamic stiffness of the rubber bushing which is acquired through the dynamic characteristic experiment. The hyper-viscoelastic constitutive model with accurate material parameter of rubber bushing is established. Subsequently the complete dynamic characteristic information of rubber bushing is reconstructed.

The technique in this study greatly shortens the development cycle and reduces expenditure on researching rubber-likes material.With the role of guiding researching the dynamic characteristics of the rubberlike，the technique is also applicable to study the static characteristics of rubber-like.Meanwhile，the significance of the method for the design and development of rubber bushing is profound.

Acknowledgements

This paper is supported by Open Fund of Key Laboratory of Advanced Manufacturing Technology for Automobile Parts，Ministry of Education，Chongqing University of Technology and Innovation Fund of Postgraduate for Chongqing University of Technology（YCX2013208）.

［1］Blundell M V.Influence of rubber bush compliance on vehicle suspension movement［J］.Materials&Design，1998，19（12）：29-37.

［2］Ogden R W.Nearly isotopic elastic deformations：application to rubberlike Solids［J］.Journal of the Mechanics and Physics of Solids，1978，26（1）：37-5.

［3］Charlton D J，Yang J，The K K.A review of methods to characterize rubber elastic behavior for use in finite element analysis［J］.Rubber Chemistry and Technology，1994，67（3）：481-503.

［4］Sasso M，Palmieria G，Chiappinia G，etal.Characterization of hyperelastic rubber-like aterials by biaxial and uniaxial stretching tests based on optical methods［J］.Polymer Testing，2008，27（8）：995-1004.

［5］Gang Lei，Qian Chen，Ying Liu，and JingJing Jiang.An Inverse Method to reconstruct complete stiffness information of rubber bushing［J］.Advances in Materials Science and Endineering，2014（10）.

［6］Zhang Wenfei.Powertrain Rubber Mounting Constitutive Relation and Optimization［D］.Beijing：Tsinghua University，2012.

［7］Pan Xiaoyiong.An investigation on modeling and calculation methods for dynamic properties of a rubber isolator［D］. Hangzhou：Zhejiang University of technology，2009.

［8］Li Xiaofang，Yang Xiaofan.A review of elastic constitutive model for rubber materials［J］.China Elastomerics，2005，15（1）：55-58.

考虑橡胶衬套超-粘弹性的动态参数识别

雷 刚1，2*，刘 莹1，胡 鹏2，陈 茜1
1.重庆理工大学汽车零部件先进制造技术教育部重点实验室，重庆 400054
2.重庆市科学技术研究院重庆轨道交通与汽车（摩托车）零部件研究中心，重庆 400054

以某车麦弗逊悬架控制臂橡胶衬套为研究对象，建立了基于橡胶衬套超-粘弹性本构模型的有限元仿真模型，并将动态特性仿真结果与试验数据进行对比；利用动态特性试验数据，采用仿真软件识别得到与橡胶衬套匹配度较高的频域粘弹性本构模型参数；结合非线性有限元软件分析得到橡胶衬套动态特性迟滞回线和阻尼角信息，完成橡胶衬套动态参数识别。

橡胶衬套；超-粘弹性本构模型；动态参数识别

10.3969/j.issn.1001-3881.2015.12.015Document code：A

U279.3+24

21 October 2014；revised 22 February 2015；accepted 7 March 2015

*Corresponding author：Gang LEI，Professor.

E-mail：499151022@qq.com

book=94,ebook=97