基于小波分析和GM-ARIMA模型的月度售电量预测

樊 娇，冯 昊，牛东晓，王筱雨，刘福炎

(1.华北电力大学经济与管理学院，北京 102206;2.国网浙江省电力公司经济技术研究院，浙江杭州 310008)

0 引言

随着电力体制改革的深化和电力市场的逐步建立与发展，电力企业运营的经济性成为重要指标。对于电力企业而言，主要的现金流入来源于售电收入，在我国目前实行电价管制的情况下，对售电量的准确预测有助于电力企业制定合理的购售电方案，确定融资缺口，安排投资支出，具有重要的实践指导意义。

目前，国内外对短期售电量的预测方法与短期负荷预测的方法相同，基本上分为传统预测法及智能预测法两类。传统预测方法主要有经典法、回归分析法、时间序列法、指数平滑法等;传统预测方法多基于时间序列本身的特征，对不同类型的售电量预测没有统一而合理的处理方法，在气候条件、节假日等的影响下稳定性较差［1－2］。智能预测方法主要包括小波分析法、混沌预测法、模糊理论预测法、人工神经网络预测法等。智能预测方法能有效利用历史数据，并考虑某些复杂因素，多数具备自我学习能力和自适应推理能力，通用性较强［3］。

小波分析是继傅里叶变换和短时傅里叶变换后发展起来的一种时频局部化信号分析方法。目前小波分析在信号处理、语音编码、模式识别及许多非线性科学领域内取得了大量的研究成果。小波分析得到广泛应用的原因在于它在时域和频域同时具有良好的局部性质，能将时间序列分解成交织在一起的多尺度成分，从而能够不断地聚集到所研究对象的任意微小细节［4－5］。本文提出了基于小波分析的月度售电量预测新方法，通过小波函数将时间序列分解，对经小波变换后不同尺度上的时间序列进行特征分析，然后选用相匹配的模型进行预测，重构后得出预测结果。实证算例表明，基于小波分析和GM-ARIMA 的组合预测方法具有较高的精度和适应能力，是一种有效的短期电量预测方法。

1 小波分析理论

小波分析是一种时域—频域分析方法，它在时域和频域上同时具有良好的局部化性质，并且能根据信号频率高低自动调节采样的疏密，容易捕捉和分析微弱信号，尤其是对奇异信号很敏感，能很好的处理微弱或突变的信号，其目标是将一个信号的信息转化成小波系数，可以方便的处理、存储、传递、分析或用于重建原始信号，这些优点决定了小波分析可以有效地应用于电量预测问题［6－8］。通过对电量序列进行小波变换，将原始序列投影到不同的尺度上，得到若干子序列，对不同序列分别建立不同的模型进行预测，然后通过序列重构得到完整的预测结果，该方法不但可提高预测精度，而且可以提高建模效率。

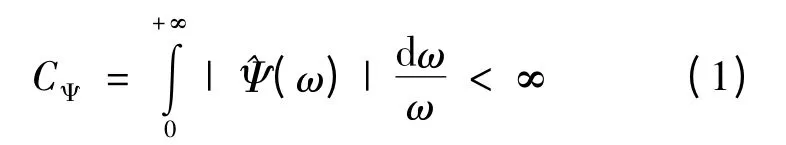
则函数Ψ(t)称为母小波。将母小波通过伸缩平移而生成一簇小波序列{Ψa，b(t)}:

则函数{Ψa，b(t)}称为子小波，其中a 为尺度因子，对母小波作伸缩;b 为平移因子，对母小波作平移［9－10］。小波变换的小波函数具有不唯一性，同一个工程问题用不同的小波函数进行分析有时结果相差甚远。本文的数据处理过程分为4步:

(1)结合历史数据序列特征，选用合适的小波分解函数和分解尺度对原始售电量时间序列进行分解，得到各分解子序列的波形和序列值。

(2)分析子序列的特征，分别运用GM(1，1)和ARIMA 模型对分解后的近似序列和细节序列进行预测。

(3)将第二步中预测出来的各个新序列进行重构产生最终的预测序列。

(4)将得到的预测序列和原始序列进行比较，计算误差率，同时与常用预测模型的预测结果比较，验证该模型的预测效果［11－12］。

2 实例分析

2.1 原始数据分析

为了检验预测模型的可行性，我们选取Z 省2011年1 月至2014年10 月共46 个月度售电量数据作为模型的原始数据，并用2014年1－10 月的数据作为验证数据，然后对11，12 月的售电量进行预测，最后将预测结果和实际值进行比较，求出误差率进而验证模型的有效性。Z 省是我国的经济发达省份，根据该省电力公司财务报表数据，描绘其2011年1 月到2014年10 月的月度售电量的时序图如图1所示，万kW·h。

从图1 中我们可以看出，Z 省月度售电量长期而言呈现逐步上升的趋势，一年内数据序列呈凸形状，即自每年初起数据序列开始逐步上升，在八月左右达到峰值，此后开始逐渐降低直至年底，在下年初再次逐渐升高，达到高于上年的顶峰，总体而言，该曲线呈现一个具有多周期性的非平稳过程。

图1 月度售电量时序图Fig.1 Time series of month electricity sales

2.2 小波函数及分解尺度选择

母小波应根据售电量序列的特点进行选择，同时还需要通过构造不同小波基对售电量序列进行分解并对变换结果进行比较，选取最能体现各子序列规律的母小波。本文通过分析原序列波形，选择四阶Daubechies 函数db4 为母小波。在一定的预测要求下，分解尺度如果选择太小，则不能有效地将原信号中具有不同的频率特征的分量分离出来;而太大的话则需要用较多的模型对分解后的各分量进行预测，各个模型都会引入一定的误差，从而导致最终预测误差变大;在通过大量数据进行多次分析之后本文选择3 尺度对售电量序列进行分解［13］。

图2 小波分解序列Fig.2 Wavelet decompisition series

2.3 小波分解

本文利用MATLAB 软件对图1 中的售电量时间序列数据进行小波分解，采用Daubechies 函数db4 小波函数，分解水平为3，MATLAB 软件输出分解后的近似序列和细节序列如图2所示，其中Approximation A3 为近似序列，Detail D1，Detail D2和Detail D3 分别为各分解尺度对应的细节序列。

2.4 分解子序列预测

(1)近似序列的灰色模型预测

由图2 中的近似序列Approximation A3 变化趋势可以看出该序列反映了售电量稳步增长的趋势，本文由于样本数据较少，采用常用的BP 神经网络预测近似序列会导致学习效果欠佳，因此本文采用GM(1，1)对近似序列进行预测，以合理预测序列的增长趋势。灰色预测通过鉴别系统因素之间发展趋势的相异程度，即进行关联分析，对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况。其用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型，预测未来某一时刻的特征量，对样本数据量要求不高［14］。对于近似序列根据GM(1，1)模型预测结果如表1所示。

(2)细节序列的ARIMA 模型预测

根据图2 显示的小波分解后的各尺度细节序列具有较为平稳的性质，本文采用ARIMA 模型进行预测。ARIMA 模型全称为差分自回归移动平均模型(Autoregressive Integrated Moving Average Model)，在模型ARIMA(p，d，q)中，AR 是自回归，p 为自回归项;MA 为移动平均，q 为移动平均项数，d 为时间序列成为平稳时所做的差分次数［15］。

根据小波分析理论，随着尺度空间阶数增大，原序列在此尺度空间中投影得到的序列具有越来越好的线性及平稳性。我们用EVIEWS 软件进行单位根检验判断序列的平稳性，在平稳序列自相关和偏自相关图的基础上，确定p，q 值，从而进行数值预测。本文根据分解出的细节数序列D1，D2，D3 分别构建模型ARIMA(4，1，1)，ARIMA(2，0，1)及ARIMA(2，0，2)进行预测，预测结果如表1所示。

表1 各分解序列预测结果Tab.1 Prediction results of each decomposed sequence

2.5 预测结果比较

在各分解序列预测的基础上，通过将近似序列与细节序列的预测值重构可得到最终的月度售电量预测结果，与2014年1～10 月份的实际售电量相比，可计算出误差率，如表2所示，为直观反映预测效果，绘制预测值与实际值比较情况如图3所示。

表2 预测结果及误差Tab.2 Prediction results and errors

表2 及图3 显示了采用小波分析和GM-ARIMA 组合预测模型预测出的售电量与实际值的比较，可以看出，该预测模型最大误差率为11.03%，出现在2 月份，这是由于每年春节出现在1 月或2月不同所致，最小误差率为0.34%，平均误差率为3.7%，预测精度较高;同时可以看出2014年8 月份的预测绝对误差较大，与Z 省8 月份气温明显低于往常年份有关。

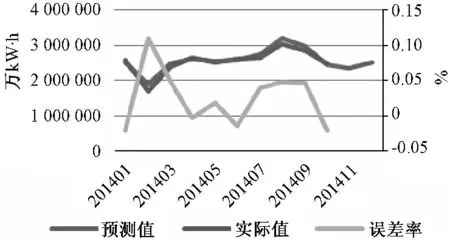
图3 预测值与实际值比较Fig.3 Comparison between actual values and prediction values

表3 多种预测方法预测结果及误差率比较Tab.3 Comparison among various forecast methods

此外，本文分别采用BP 神经网络、ARIMA 模型及灰色模型对原始数据进行了直接预测，将预测结果与小波分析后的GM-ARIMA 组合模型预测结果进行误差率比较，如表3所示，可以看出本文提出的组合预测模型预测精度明显较高，具有较强的适应能力。

3 结论

本文提出小波分析和GM-ARIMA 组合预测模型对Z 省的月度售电量进行预测，研究表明原始序列经过小波分解重构后，能细致地刻画各种随机干扰因素对售电量变化的影响;通过对不同的分解序列采用相匹配的预测模型进行处理，可以有效地提高预测精度，克服单一预测方法的自身缺点;最后通过与常用预测方法的预测误差比较，证明该方法具有较高的预测精度和适应能力，是一种有效的月度电量预测方法。基于小波分析的组合预测方法原理简单，预测模型容易实现，可为短期电量预测工作提供有力支持。

通过本文分析可以看出，小波分解函数及分解尺度的选择对模型预测的准确性有一定影响，目前往往是通过经验或通过不断试验对结果进行对照分析来选择，这也是研究的难点所在;另外由于本文数据样本量较小，对预测结果有较大影响。在下一步的研究中，可在适当扩大样本容量的基础上，对小波分解函数及分解尺度的确定进行进一步研究。

［1］石恒初，严正，黄涛，等.基于小波分析的短期电力负荷组合预测方法［J］.继电器，2007，35(17):22－26

［2］胡昌华，李国华，刘涛，等.基于MATLAB 6.x的系统分析与设计－小波分析［M］.西安:西安电子科技大学出版社，2008.

［3］宋超，黄民翔，叶剑斌.小波分析方法在电力系统短期负荷预测中的应用［J］.电力系统及其自动化学报，2002，14 (3):8－12

［4］叶淳铮，常鲜戎，顾为国.基于小波变换和支持向量机的电力系统短期负荷预测［J］.电力系统保护与控制，2009，37 (14):41－45.

［5］邰能灵，侯志俭，李涛，等.基于小波分析的电力系统短期负荷预测方法［J］.中国电机工程学报，2003，23 (1):45－50.

［6］姚李孝，刘学琴.基于小波分析的月度负荷组合预测［J］.电网技术，2007，31 (19):65－68.

［7］于晓铭.基于小波分析和支持向量机的电力短期负荷预测［D］.天津:天津大学，2009.

［8］孙云.小波分析在电力系统短期负荷预测中的应用研究［D］.杭州:浙江大学，2005:13－20.

［9］Huang S J，Shih K R.Short-term Load Forecasting via ARMA Model Identification Including Non-Gaussian Process Considerations［J］.IEEE Transactions on Power Systems，2003，18 (2):673－679.

［10］胡力，何怡刚.小波－LMBP 网络在短期负荷预测中的研究与应用［J］.电力系统及其自动化学报，2010，22 (5):46－50.

［11］顾洁.应用小波分析进行短期负荷预测［J］.电力系统及其自动化学报，2003，15 (2):40－ 44，65.

［12］冉启文，单永正，王骐，等.电力系统短期负荷预报的小波－神经网络－PARIMA 方法［J］.中国电机工程学报，2003，23 (3):38－42

［13］Zhou M，Yan Z，Ni Y X，et al.Electricity Price Forecasting with Confidence-interval Estimation through an Extended ARIMA Approach［J］.IEE Proceedings-Generation，Transmission and Distribution，2006，153(2):187－195.

［14］陈志业，牛东晓，张英怀，等.电网短期电力负荷预测系统的研究［J］.中国电机工程学报，1995，15 (1):30－35.

［15］周明，聂艳丽，李庚银，等.基于小波分析的短期电价ARIMA 预测方法［J］.电网技术，2005，29(9):50－55.