直埋单芯电缆的载流量数值计算

燕 怒，朱攀勇，熊晓晨

(1.三峡大学机械与动力学院，湖北宜昌 443002;2.武汉纺织大学机械工程与自动化学院，湖北武汉 430073)

0 引言

电力电缆的载流量涉及到输电线路的安全和经济以及其寿命问题。近年来，随着经济的快速发展，社会对电力的需求日益增长［1］，如何在保证安全的前提下最大限度提高输电线路的输送容量将显得非常重要。因此，载流量的精确确定具有重要的现实意义［2－4］。电缆载流量计算最早由A.E.Kenelly 于19 世纪末开始研究，计算方法非常简单。随后Neher 和McGrath 在1957年提出了NM理论［5］。国际电工委员会(IEC)在McGrath 的研究基础上于1982年提出了电缆额定载流量计算标准IEC60287［6］，在1985年又提出电缆暂态载流量计算标准IEC60853。目前世界上大多数国家都以IEC 标准作为电缆产品额定载流量的依据。但是IEC 标准仅仅是载流量的解析计算方法，而实际工程应用问题中它存在许多局限性，它忽略了电磁场与热力场的耦合、多回路间的电磁感应和土壤水分迁移等问题，这些因素又会直接影响到IEC 标准计算中电缆各层及周围煤质的热阻值，这样造成IEC 标准计算的载流量值相对实际值有偏差［7］。

为了解决IEC 标准计算存在的不足，国内外学者对此做了大量研究。我国起步较晚，在近年来才开始电缆的数值计算方面研究。文献［8］提出了在IEC60287 解析计算基础上结合迭代法计算载流量的新思路。文献［9］用IEC60287 解析计算结合迭代法计算了一端接地时500 mm2和800 mm2的电缆载流量。文献［10］提出了载流量数值计算方法，首次将有限元计算温度场与迭代法计算载流量相结合，建立了电缆群温度场模型，为载流量数值计算的发展奠定了一定的基础，然而他们的有限元计算得出的温度分布图参考了文献［11］中的温度分布图，由于不同的电缆和不同的敷设环境温度分布存在差异，这使得计算结果的准确性有待商榷。文献［12］对有限元计算电缆群温度场做了理论论述，同时提出了用弦截法计算载流量的新方法。但是，其温度场结果并没得到详细的推导验证。文献［2］综述了载流量解析计算和数值计算的具体计算方法以及它们存在的不足和优点，最后对载流量的计算做了展望。文献［13］运用Matlab 软件对排管敷设电缆温度场做了仿真，采用迭代法求解载流量，温度场仿真结果相对真实值存在误差。

有限元法可以计算条件较复杂的载流量，相对IEC 标准解析计算灵活、准确。在有限元结果温度场的处理方法上迭代法和弦截法都是求得载流量较理想的方法。迭代法和弦截法虽然从理论上可以得到载流量的精确值，但是实际计算过程中，每一次迭代(包括弦截法)都需要做一次有限元仿真，如果迭代收敛较快可能只需要做几次有限元仿真就可以得到理想的结果，反之需要做数十次甚至数百次有限元仿真计算。

本文对直埋电缆载流量的有限元算法的思路和原理做了详细的论述，运用ANSYS 软件对电缆温度分布图做了八次加载仿真，以最小二乘法为基础，运用Matlab 对八次仿真结果曲线拟合线芯温度与载流量的函数曲线。根据函数曲线求得电缆载流量。

1 电缆群温度场有限元计算原理

电力电缆载流量的有限元计算涉及电缆群温度场的有限元计算和以电缆群温度场为基础的载流量的数值计算。电缆群温度场的有限元计算模型是结合热力学知识的二维稳态热导模型。

1.1 电缆群温度场有限元计算思路

电缆群稳态温度场是二维稳态热导问题，二维稳态温度场的控制方程为

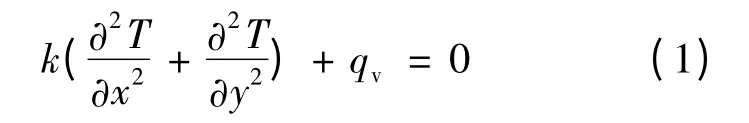
式中:k 为介质的热传导系数，W/(m·K);T 为点(x，y)处的温度，℃;qv为体积发热率，W/m3(无热源区域qv=0)。

边界条件描述的是温度场在边界上的状况。温度场的热传导有三类边界条件，分别是已知边界温度边界条件、已知边界法向热流密度边界条件、对流边界条件。三类边界方程式如方程式(2)～(4)所示。

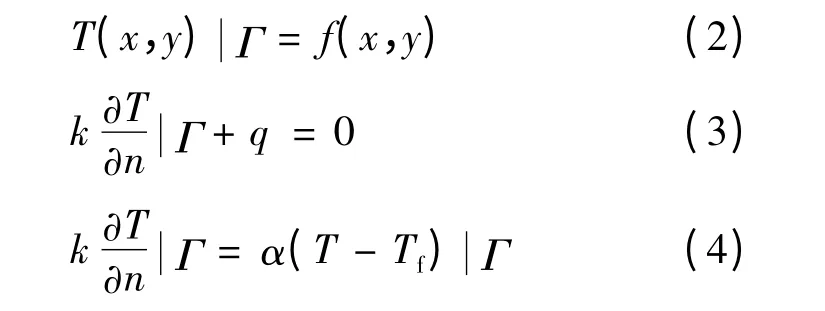
式中:q 为热流密度，W/m2;Tf为流体温度，℃;α为对流换热系数，W/(m2·K);Γ 为积分边界

有限元计算温度场的基本思路:根据控制条件(1)及边界条件(2)、(3)、(4)创造一个温度场的泛函，然后运用变分法推导有限元方程，以及求解有限元方程。

1.2 温度场泛函表达式

泛函表达式包括控制方程(1)，边界条件(2)、(3)、(4)式的全部内容，创造泛函(5)。

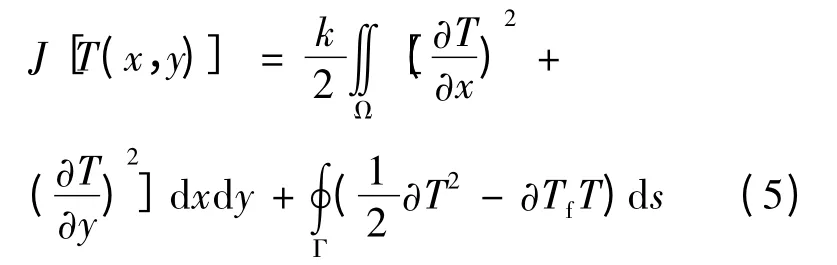
1.3 有限元方程推导及求解

有限元方程求解的基本思路:将求解域离散成若干三角单元，任取一个三角单元进行分析如图1，可得到未知节点温度的多元函数，将泛函转化为多节点形式运用变分法求极值得到节点的温度刚阵，最后用高斯消元法求解即可。在边界线上的任一点的温度T，可用两个端点的节点温度线性插值函数(6)表示。

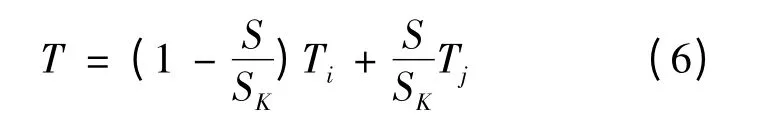
从温度场插值函数(6)可知，温度场已离散到全部节点上，即求温度场实际是求节点的温度值。用变分法求得有限元刚阵:利用高斯消元对(7)求解可得到各节点的温度值。

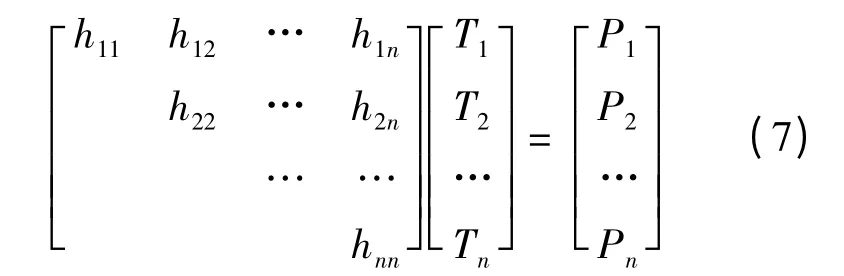
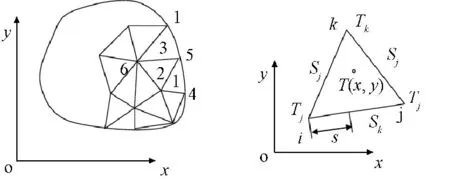
图1 单元内任一点温度Fig.1 Temperature of any point in the unit

2 载流量计算原理

载流量是指线芯温度达到90 ℃时，电缆中通过的电流。在电缆群温度场的有限元计算中通过加载某一电流得到电缆群二维暂态温度分布函数(7)，载流量的计算基于IEC60287 标准。图2 为基于IEC60287 单芯电缆等效热路［2］。有限元计算出温度场后，可直接将温度值带入IEC 计算公式，根据参数值求得载流量。图中:θ 为导电线芯温度;θ0为电缆表面温度;W 为导电线芯电阻损耗;Wd为绝缘介质损耗;λ1W 为金属护套(和屏蔽层)电阻损耗;λ2W 为铠装层电阻损耗;λ1为金属套(和屏蔽层)损耗系数;λ2为铠装层的损耗系数;T1、T2、T3分别为绝缘、内垫衬层、外护层的热阻;T4为电缆和周围媒质的热阻。

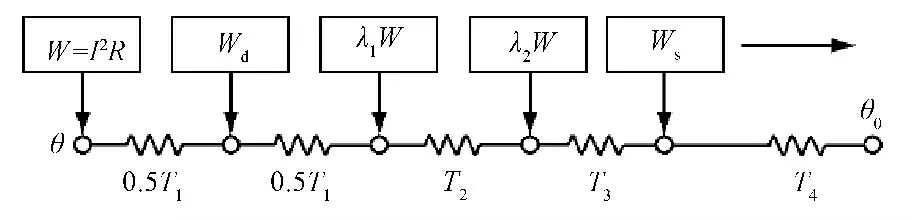
图2 单芯电缆等效热路Fig.2 Equivalent thermal circuit of single-core cable

3 电缆温度场仿真与载流量数值计算

电缆温度场用有限元软件ANSYS 仿真得到温度场结果之后，将所有结果和加载电流进行最小二乘法曲线拟合得到温度与载流量的函数曲线，再通过函数曲线可求得线芯温度90 ℃时的加载电流，即载流量。

3.1 电缆温度场仿真

以最常用的的交联聚乙烯绝缘电缆YJLW02－64/110kv.1 ×300 mm2为计算实例有限元仿真过程如下:

(1)定义计算模型单元类型。

(2)根据电缆结构(表1)及敷设环境(表2)定义材料属性(表3)。

(3)建立电缆模型。

(4)布尔运算将模型进行叠分操作以及对模型赋予特性使模型的不同的Element 对应相应的材料属性。

(5)有限元网格划分，如图3所示。

表1 电缆结构参数Tab.1 Values of the structural

表2 电缆敷设环境参数Tab.2 Values of the laying environment

表3 电缆材料属性参数Tab.3 Values of the material properties

(6)施加载荷及约束，本次共施加了8 种电流值:610、620、630、640、650、660、670 和680 A，施加载荷电流值参照IEC60287 标准算得的载流量，8 次载荷分布在IEC60287 标准载流量值左右。

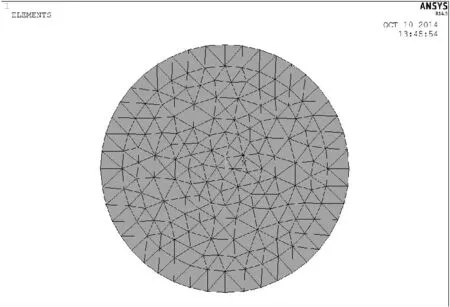
图3 YJLW02－64/110kV.1 ×300mm2 有限元网格划分模型Fig.3 The finite element mesh model of YJLW02－64/110kV.1 ×300 mm2

(7)求解得到模型温度分布云图，图4 列出了部分加载电流下的电缆温度分布云图。

3.2 电缆载流量数值计算

加载8 次电流得到8 个电缆温度分布云图，将8 次载荷电流与求得的温度导入Matlab 软件，拟合加载电流与导体温度的函数曲线。得到线芯温度值－载荷电流值离散点，将离散点拟合得到线芯温度值－载荷电流值曲线。

由图5 线芯温度值－载荷电流值拟合曲线可求得90 ℃时，加载电流值为649 A，YJLW02－64/110 kV.1 ×300 mm2电缆在埋设深度为0.7 m，土壤热阻为1.0 K/W，空气温度25 ℃，土壤温度20 ℃，电缆间距0.2 m 的条件下的载流量值为649 A。

图4 不同加载电流下的温度分布云图Fig.4 Temperature distribution under different loading current

有限元计算得到的载流量值为649 A 相对解析计算结果632 A 偏大，但差值不是很明显。说明在确定条件下有限元计算得到的载流量值与IEC60287 标准计算的值并没有太大偏差，其主要原因在于确定的敷设条件下的解析计算采用的热阻值相对于复杂的敷设环境下的热阻更接近实际值。工程实践运用更广泛的是解析计算，但是解析计算忽略了多场的耦合问题［2］，将热阻尤其是土壤的热阻值取为确定常数［15］，同时又为了保证电缆的安全运行，所以采用的热阻通常比实际值大，这样计算得出的载流量偏小［16］。由此可见有限元计算的载流量更接近真实值。但数值计算的结果的准确性还有待通过实验来进行验证，由于目前实验模拟真实封闭环境条件以及相关测试测量设备准确度不高等原因，暂时还无较好的解决方案，还有待于后续研究能够有所突破。

若电缆周围存在热源(热水管道或蒸汽管道等)则需考虑热源对电缆温度场以及周围敷设环境参数的影响。由于热源会影响土壤热阻以及电缆各层和周围环境导热能力等，因此在存在热源的条件下需对表2 中电缆敷设环境参数以及表3中电缆材料属性参数重新查阅计算。

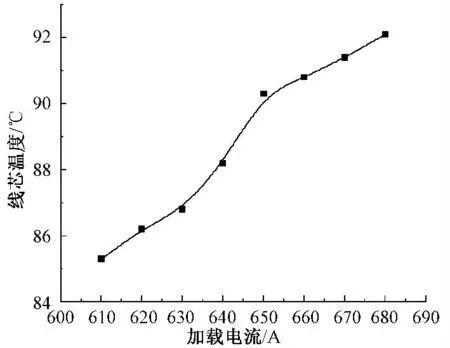
图5 线芯温度值－载荷电流值拟合曲线Fig.5 The fitted curves of conductor temperature-loading current

数值计算省略了繁琐且难以精确计算的热阻参数，同时也不必计算导体的交流电阻值即可以获得不同环境温度下的载流量和温度参数，而且数值计算结果更接近真实值，所以对于单芯直埋电缆的载流量计算，采用数值计算相对解析计算更加可靠。

4 结论

通过多次加载电流得到的温度分布云图得到线芯温度值－载荷电流值拟合曲线，再利用拟合曲线可求得90 ℃时，加载电流值为649 A，YJLW02－64/110 kV.1 ×300 mm2电缆在埋设深度为0.7 m、土壤热阻为1.0 K/W、空气温度25℃、土壤温度20 ℃和电缆间距0.2 m 的条件下的载流量值为649 A。将计算结果与IEC60287 标准计算值632 A 进行比较对比分析，有限元计算的载流量更接近真实值。

［1］陈锡阳，王艳玲，黄河，等.一种新的架空输电线路安全限距计算模型［J］.电力科学与工程，2015，31 (2):60－65.

［2］郑雁翎，王宁，李洪杰，等.电力电缆载流量计算的研究与发展［J］.电线电缆，2012，(2):4－9.

［3］张洪麟，唐军，陈伟根.基于有限元法的地下电缆群温度场及载流量的仿真计算［J］.高压电器，2010，46 (2):42－45，51.

［4］王红斌，陈扬，高雅，等.输电线路弧垂对动态增容的影响［J］.华北电力大学学报，2014，41(2):41－46.

［5］Pollak P.Neher McGrath calculations for insulated power cables［C］.Industrial and Commercial Power Systems Technical Conference 1984，Atlanta，GA，USA，7－10 May，1984:172－175.

［6］IEC 60287，电缆载流量计算系列标准［S］.

［7］Anders G J，Radhakrishna H S.Power cable thermal analysis with consideration of heat and moisture transfer in the soil［J］.IEEE Transactions on Power Delivery，1988，3 (4):1280－1288.

［8］梁永春，孟凡凤，王正刚，等.土壤直埋电缆群额定载流量的计算［J］.高压电器，2006，42 (4):244－246.

［9］牛海清，王晓兵，张尧.基于迭代法的单芯电缆载流量的研究［J］.高电压技术，2006，32 (11):41－44.

［10］孟凡风，李香龙，徐燕飞.地下直埋电缆温度场和载流量的数值计算［J］.绝缘材料，2006，39(4):59－61，64.

［11］Garrido C，Otero A F，Cidras J.Theoretical model to calculate steady-state and transient ampacity and temperature in buried cables［J］.IEEE Transactions on Power Delivery，2003，18 (3):667－678.

［12］梁永春，李彦明，柴进爱，等.地下电缆群稳态温度场和载流量计算新方法［J］.电工技术学报，2007，22 (8):185－190.

［13］郑雁翎，许志亮，张冠军，等.采用Matlab 仿真的变电站高压进线温度场和载流量数值计算［J］.高电压技术，2012，38 (3):566－572.

［14］梁永春，柴进爱，李彦明，等.基于FEM 的直埋电缆载流量与外部环境关系的计算［J］.电工电能新技术，2007，26 (4):10－13.

［15］范玉军.一种电缆载流量及温度参数的换算方法［J］.电线电缆，2014，(2):4－5.

［16］黄诗雅.土壤直埋敷设单芯电力电缆温度场与载流量计算［J］.武汉大学学报(工学版)，2014，47(4)，502－505，526.