一种星箭动态界面力识别方法

张永涛 周徐斌 杜冬 王建炜 石川千

（上海卫星工程研究所，上海 200240）

1 引言

卫星与运载火箭界面的载荷特性是卫星结构设计的重要依据。国内外运载火箭用户手册都以准静态加速度的形式，详细规定了星箭界面的三向载荷条件，这是卫星结构设计必须遵循的安全准则，同时也是对卫星整体进行力学环境试验考核的主要标准之一［1］。尤其是近年来，国内外认识到星箭连接试验夹具的机械阻抗与真实飞行构型中安装结构的机械阻抗存在很大的差异，仅采用加速度条件作为控制条件可能导致严重的“过试验”问题［2-4］，因此逐步开始重视在传统的加速度控制基础上增加界面力控制（力限控制）来解决振动试验输入问题［5-7］。综上，准确掌握星箭界面力载荷状态具有十分重要的工程意义。

要测定发射过程中星箭界面的力谱，最直接的方法是在卫星与运载火箭之间串入力传感器作为测力装置［8］。但这对力传感器和连接结构提出了较高的研制要求，同时会削弱界面处的连接刚度和强度，将对星箭耦合结构的整体力学特性产生明显改变，从而会给发射段的承载安全性带来风险。

为避免串联力传感器，本文提出了一种通过测量星箭连接环应变来计算星箭界面力的方法，并经仿真分析，验证了该方法的有效性和工程适用性，可以为卫星力限控制振动试验输入谱的确定提供一定参考。

2 理论分析

通常卫星的底部由星箭连接环、承力筒、底板与隔板等结构组成（如东方红三号，东方红四号等卫星）［9］。星箭连接环处在卫星的最底部，它连接着卫星承力筒与运载火箭的端口。

将星箭连接环考虑为薄壁圆筒，如图1 所示。采用梁弯曲时的平面截面经典假设，对其进行受力分析。

F为施加在薄壁圆筒底部的六自由度载荷，表示星箭界面的六自由度界面力。

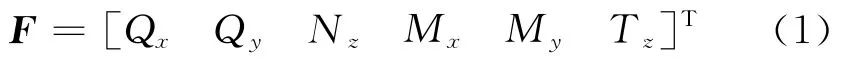
式中：Qx和Qy为剪力，Nz为轴力，Mx和My为弯矩，Tz为扭矩。

根据欧拉-伯努利梁假设，轴向应力和剪应力为

式中：σ为沿z轴方向的轴向应力，τ为x、y平面内的剪应力。

因此，由薄壁圆筒圆周3个位置（θ1，θ2，θ3）的各向应力便可计算得到载荷F，设系数矩阵B满足以下方程：

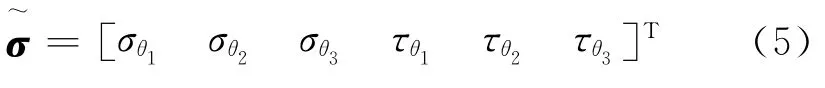
式中：θi（i＝1，2，3）表示应力σ与τ在圆周坐标θ上的测点位置。

根据式（1）～（5），得到系数矩阵B如式（6）所示。

可见，界面力F可由测点应力计算得到。而应力又可根据材料本构关系由应变得到。本方案使用三向应变花［10］粘贴在连接环的表面测量应变。通常使用的应变花如图2所示。

图2 在界面力识别方法中使用的应变花Fig．2 Strain rosette used in the identification method

轴向应变εz，环向应变εθ，剪应变γθz如式（7）所示。

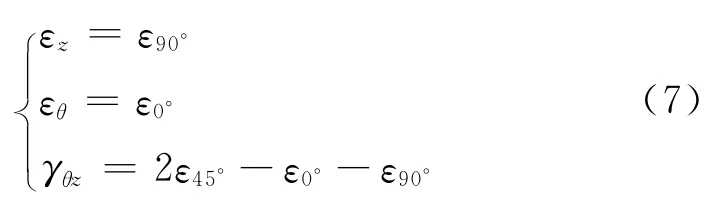
式中：下标0°，45°或90°表示图2中应变花各敏感栅的封装方向。

根据平面应力状态的本构关系，可得到应力的表达式如下：

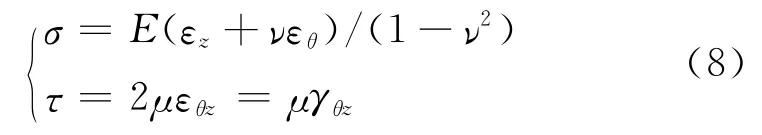
式中：μ为拉梅常数，它可以由材料的弹性模量E与泊松比ν计算得到。

假设存在系数矩阵K1、K2满足式（10）。

式中：θ1，θ2，θ3表示应变花在星箭连接环圆周上的粘贴位置。

根据式（7）～（11）可得

将式（10）代入式（4），则有

式中：F为施加在薄壁圆筒底部的六自由度载荷是应变向量。

综上，可以通过在星箭连接环圆周上相同高度处布置3个应变花监测应变，然后根据式（14）可计算出六自由度的星箭界面力。

3 影响要素研究

3．1 理论假设的合理性验证

为验证理论假设的合理性，考虑到中心承力筒是卫星中常见的典型结构，建立了如图3所示的有限元模型。

图3中的模型模拟了一个直径1m，高度2m，厚度5mm 的铝合金圆筒在一端固支、另一端施加集中力时的状态。

验证如下：

（1）在筒外壁中部圆周方向均匀布置60个测点（即相邻测点间隔6°），任取3 个测点为一组形成34 220种不同的测点组；

（2）读取各组测点应变值，用式（14）计算对应界面力，并将此界面力对仿真数值求相对误差。

图3 按理论分析要求建立的模型Fig．3 Model based on theoretical analysis

验证结果如图4 所示，图中横轴为测点组序号，纵轴为界面力各分量识别的相对误差（在半对数坐标系中表示）。

从图4可以看出，除轴向力的识别相对误差最大为0．02（2%），其他方向载荷的识别误差均在0．3%以下。

仿真中，在筒顶部施加的载荷为［200N，250N，290N，70N·m，40N·m，190N·m］。为避免载荷的特殊性，选取了多组其它工况对数据进行相同的处理，发现其相对误差的大小几乎不受影响，仅仅是最大相对误差出现的测点组发生了变化。下面的仿真中也有相似的结论，因此简化起见，可以采用特殊的工况探究一般的结论。

综上，可以判定，该界面力识别方法对薄壁圆筒结构是适用的，而且其识别精度较高。同时考虑到施力点部位都与应变测点的位置存在高度上的差异，因此需要进行力和力矩的平移操作，仿真结果证明这种平移对识别结果影响很小。

图4 界面力识别误差Fig．4 Identification error of interface force

3．2 应变测点布置优化

据3．1节的分析结果，只要满足式（2）、（3）成立的条件，考虑力和力矩平移之后界面力的识别效果几乎不受测点布置高度的影响。但在筒下端附近存在边界约束导致应变在高度方向上会发生变化。实际卫星结构中的连接环是短环（如图5所示），测点很有可能因过于接近下端部导致界面力识别效果变得很差。

图5 某卫星有限元模型Fig．5 Finite element model of a satellite

另外，连接环上安装有其他结构（底板、隔板等），从而产生新的约束，即星箭连接环与理想薄壁圆筒结构相差较大。

因此为了验证该识别方案对卫星结构的适用性，下文中以我国某气象卫星的技术状态为背景建立了多个仿真模型，其中连接环材料均为铝合金，直径为1m，高度为0．8m，厚度为0．05m。利用仿真模型逐个评估测点高度、底板对连接环的约束、隔板引起的局部应力畸变等对界面力识别的影响。

3．2．1 测点高度的影响

对图3模型的测点高度进行变化，形成不同高度的测点分布圆周，在每个圆周上仍然均匀布置60个测点（即相邻测点间隔6°），任取3个测点为一组形成34 220种不同的测点组。

选取各组测点应变，利用式（14）计算对应界面力，并将界面力对仿真读取结果求相对误差，从而得到反映综合误差情况的误差柱形图（见图6）。

图6即为图3模型界面力识别误差随测点高度变化的误差柱形图，横轴表示测点所处高度与薄壁圆筒直径的比值，纵轴表示该工况所有测点组合计算界面力相对误差的最大值。

图6 界面力识别误差随测点高度变化Fig．6 Identification error variation with arranged height point for the ideal model

从图6中可以看出，当测点布置高度为筒直径的4%以上时，筒下端约束的影响可以不用考虑（各向力识别误差均在2%以下）。反之，相对识别误差会变得很大（当高度直径比为0．2%时，个别方向载荷相对误差大于20%）。

由此得到结论：识别界面力时应变测点应远离连接环端面，其布置高度应大于直径的4%。

3．2．2 底板约束的影响

建立如图7所示有限元模型，即在星箭连接环中部加装了长2m，宽2 m，厚度为0．08 m 的铝合金底板，并在其顶端施加载荷［40N，60N，130N，-9N·m，24N·m，12N·m］。经验证，此特殊工况下的界面力识别误差情况可以代表一般工况。

图7 带有底板的短薄壁圆筒结构模型Fig．7 Short thin walled cylinder with baseboard model

如图7所示，在筒下端部到底板处中间高度圆周上仍然均匀布置60个测点（即相邻测点间隔6°），任取3个测点为一组形成34 220种不同的测点组。

选取各组测点应变利用式（14）计算对应界面力，并将此界面力对仿真读取结果求相对误差，然后得到反映综合误差情况的误差柱形图（见图8）。

图8即为带有底板的短薄壁圆筒结构模型界面力识别误差随测点高度变化的误差柱形图，横轴表示测点所处高度与薄壁圆筒直径的比值，纵轴表示该工况所有测点组合计算界面力相对误差的最大值。

从图8中可以看出，对于实际的星箭连接环，即当薄壁圆筒的高度较小时，界面力识别误差将显著增大，同时测点布置高度为筒直径的4%～6%时效果较好，即测点接近筒下端或者底板时，识别误差都会增大。

由此得到结论：识别界面力时应变测点除考虑到下端面约束，还应远离底板布置，距底板距离应大于筒直径的2%。

3．2．3 测点间隔的调整

通过调整测点之间的圆周角度间隔可以有效地减小识别误差。以图7中的带有底板的短薄壁圆筒结构模型为例，在由60个测点形成识别测点组的过程中，强制要求测点两两间隔角度分别大于30°、60°与90°。然后采用前述方法得到相应的误差柱形图，如图9所示。

图9 保持测点圆周不同间隔时识别误差随高度的变化Fig．9 Identification error variation with height for different angle internals

由图9可知，随着测点角度间隔的增大，界面力识别误差会显著减小。连接环上方连接底板后，若测点布置在连接环下端部与底板安装面中间的圆周上且保持测点间隔大于90°，界面力各分量识别误差均可控制在4%以内。

由此得到结论：在条件允许的情况下，测点之间的距离应尽量大一些，以减小识别误差。

3．2．4 隔板引起的局部应力畸变影响

建立如图10所示的有限元模型，即在图7模型的基础上加装4个厚度为0．08m 的铝合金隔板，工况与图7模型相同。

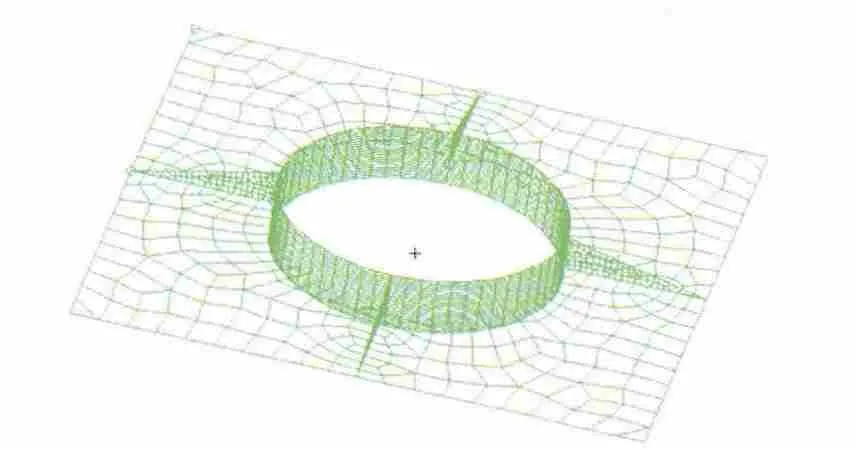
图10 带有底板与隔板的短薄壁圆筒结构模型Fig．10 Short thin walled cylinder with baseboard and clapboards model

隔板的加入会降低结构在圆周方向的对称性，因此先做静力仿真观察其应变状况。

仿真发现，对于装配不同结构的连接环，沿连接环圆周的轴向应变与剪应变基本不变，而环向应变会随结构的不同有较大差异。图11即为在受载情况下沿连接环圆周的环向应变曲线。其中，横轴表示测点圆周位置，纵轴为应变值。另外，在此基础上加入隔板，环向应变曲线（即图11中的点划线）会出现一些毛刺，在毛刺所在位置布置测点将会对界面力识别产生很大影响。图12即为图10模型在给定工况下的环向应变云图，对比图11和图12可以看出，毛刺出现在隔板附近，因此做界面力识别时，测点应远离隔板布置。

图11 连接环加装不同结构的应变响应对比Fig．11 Comparison chart for the strain response obtained from different adapter ring structures

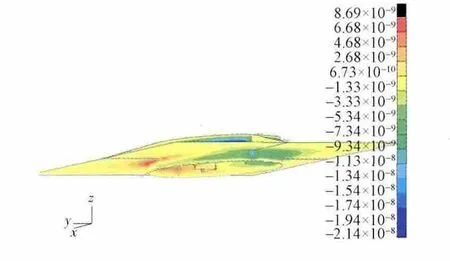
图12 模型的环向应变云图Fig．12 Circumferential strain fringe for the model

图13为带有底板与隔板的短薄壁圆筒结构模型的界面力识别误差，随测点距隔板角度距离变化的误差柱形图，横轴表示测点距隔板的角度距离，纵轴表示该工况所有测点组合计算界面力相对误差的最大值（要求测点之间角度距离大于90°）。

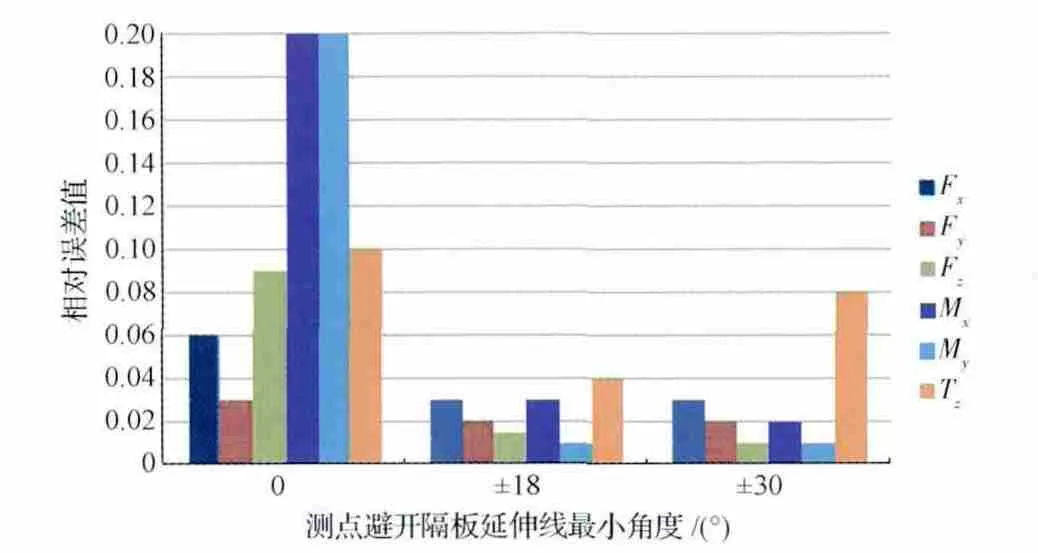
图13 模型的识别误差随距隔板角度距离的变化Fig．13 Identification error variation with the shortest angular distance from each observation point to the clapboard for the model

从图13看出，在保持测点之间角度距离大于90°时，随着测点距隔板角度距离的增大，界面力各分量的识别误差会显著减小。当角度大于30°时，各分量识别误差都小于8%。

由此得到结论：测点应远离隔板布置，并且其角度大于30°为宜。

4 动态界面力识别仿真算例

卫星升空过程中星箭界面传递动态力，因此要对该方法是否能够用于动态界面力识别进行验证。

图14是用于频响分析的卫星简化模型。它的连接环是直径为0．3m，高度为0．1m，厚度为0．02m铝合金圆柱筒。底板为厚度0．03m 的铝合金正方形板，隔板为厚度0．02m 的铝合金板并绕承力筒间隔90°分布。

图14 频响分析中使用的有限元模型Fig．14 Models used in frequency response simulation

仿真分析时，在模型底部施加动态界面力激励［12N，18N，38N，6N·m，15N·m，3N·m］，同时测点布置在前文提到的优化位置，这里取沿连接环中间高度（-52°，135°，37°）圆周位置布置。

图15为图14中所示模型的计算与实际界面力对比，图中横轴表示频率范围，纵轴表示界面力的各分量的幅值或者相位。蓝色线表示仿真结果，在此认为它是界面力的真值，红色线为利用连接环应变计算得到的界面力数值。由图15可知，各向力识别的幅值误差较小（均在20%以下），只是弯矩与扭矩的相位误差在高频段较大，识别结果可以满足工程需求。

图15 模型中的计算与实际界面力对比Fig．15 Identified and real interface forces for the model

5 结束语

针对星箭界面力监测的技术问题，本文提出了一种通过测量星箭连接环应变计算星箭界面力的方法。通过仿真分析，验证了该方法的有效性，并给出了卫星不同结构对识别误差的影响分析。研究表明，当测点间隔较大（大于90°）、远离边界（布置高度为环直径的4%～6%）且远离隔板影响区（距离隔板30°以外）布置时，此时该识别方法可以有效识别星箭界面动态载荷（幅值识别误差在20%以下），对于星箭界面力监测具有一定参考意义。

（References）

［1］中国运载火箭技术研究院．LM-3A 系列运载火箭用户手册［S］．北京：中国运载火箭技术研究院，2011 China Academy of Launch Vehicle Technology．LM-3A series launch vehicles user＇s manual issue［S］．Beijing：China Academy of Launch Vehicle Technology，2011（in Chinese）

［2］Scharton T D．Vibration-test force limits derived from frequency-shift method［J］．AIAA Journal of Spacecraft and Rockets，1995，32（2）：312-316

［3］张俊刚，庞贺伟．振动试验中力限控制技术［J］．航天器环境工程，2005，22（5）：253-256 Zhang Jungang，Pang Hewei．The force limited control technique in vibration test［J］．Spacecraft Environment Engineering，2005，22（5）：253-256（in Chinese）

［4］李正举，马兴瑞，韩增尧．振动试验力限条件设计复杂二自由度方法研究［J］．宇航学报，2011，32（1）：1-6 Li Zhengju，Ma Xingrui，Han Zengyao．Complex twodegree-of-freedom system method for force specification in force-limited vibration test［J］．Journal of Astronautics，2011，32（1）：1-6（in Chinese）

［5］Scharton T D．Force-limited vibration testing monograph［R］．Washington D．C．：NASA，1997

［6］Scharton T D．Force-limited vibration testing［R］．Washington D．C．：NASA，2012

［7］马兴瑞，韩增尧，邹元杰，等．航天器力学环境分析与条件设计研究进展［J］．宇航学报，2012，33（1）：1-12 Ma Xingrui，Han Zengyao，Zou Yuanjie，et al．Review and assessment of spacecraft mechanical environment analysis and specification determination［J］．Journal of Astronautics，2012，33（1）：1-12（in Chinese）

［8］齐晓军．航天器振动试验控制技术研究［D］．长沙：国防科学技术大学，2011 Qi Xiaojun．Research on spacecraft vibration test control technology［D］．Changcha：National University of Defense Technology，2011（in Chinese）

［9］姚骏，满孝颖，李应典，等．卫星承力筒的结构特点与应用分析［J］．电子机械工程，2010，26（3）：24-28 Yao Jun，Man Xiaoying，Li Yingdian，et al．Analysis of characteristics and applications of satellite supporting cylinder［J］．Electro-Mechanical Engineering，2010，26（3）：24-28（in Chinese）

［10］吴建星，康红普，蔡嘉芳．锚杆托盘的实验应力分析［J］．煤矿开采，2009，14（2）：58-60 Wu Jianxing，Kang Hongpu，Cai Jiafang．Experimental stress analysis of anchor bolt plate［J］．Coal Mining Technology，2009，14（2）：58-60（in Chinese）