基于MODPSO-GSA的协同空战武器目标分配

顾佼佼，赵建军*，颜骥，陈学东

(1.海军航空工程学院 科研部，烟台264001;2.91352部队，威海264208)

超视距协同空战是现代空战的主要形式，现代战机均具备多目标攻击能力，各战斗机通过相互协作，对空中多目标实施攻击.若不涉及作战战术，协同空战的核心问题为交战阶段的协同多目标分配，使我方对敌机群的攻击效果达到最优.

文献［1-2］对目前解决武器目标分配(WTA)问题的国内外研究现状进行了分析和展望:现有模型多是基于单纯的以毁伤概率越大(或剩余威胁越小)越好为准则，只考虑尽量提高杀伤效果，一次性完全分配不符合现代空战火力动态分配的实际.空战是多阶段的攻防过程，在进行武器目标分配时，要考虑在满足毁伤概率的前提下减少火力资源消耗，以备后期作战.文献［3］考虑到这个问题并提出改进，在原有目标函数上附加新的约束变量，构造一个综合的目标函数，仍是单目标决策.武器目标分配是一个多约束多变量的组合优化问题，构造一个目标函数形式复杂、求解复杂度偏高、不具备直观性且难以满足实时性等需求.

本文基于多目标决策理论构造目标分配模型并用进化多目标优化算法［4］求解，同时考虑杀伤效果和火力资源消耗，可在满足毁伤门限的前提下为指挥员提供不同耗弹量下的最优分配方案集供决策参考.模型的求解采用多目标混合离散粒子群-引力搜索算法(MODPSO-GSA)，展现了良好的寻优能力.仿真验证了该模型及其求解算法的有效性.

1 基于多目标决策的目标分配建模

某次空战，我方机群B由M架战机组成，B={i，i=1，2，…，M}，挂载导弹总数为 K，导弹集合为 A={A1，A2，…，Ar，…，AK};敌方机群 R 由 N 架飞机组成，R={j，j=1，2，…，N}.

文中基于多目标决策理论［5］构建 WTA模型，选取一次目标分配后敌方机群总期望剩余态势优势最小［6］和一次分配我方消耗导弹数量最小为两个目标函数，构造多目标决策函数为

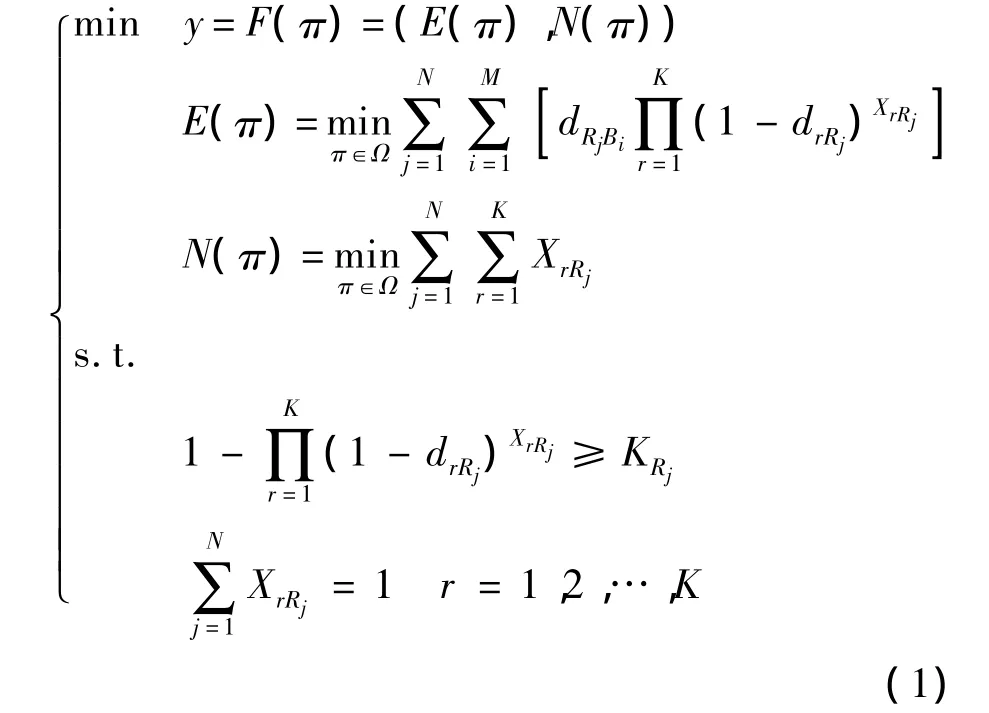
式中，E(π)为第1个目标函数;N(π)为第2个目标函数，以避免造成过度杀伤和火力浪费;Ω为导弹-目标分配空间;导弹集A中导弹Ar攻击敌机Rj为 Ar→Rj，对敌机 Rj的摧毁概率为 drRj;XrRj为二值函数，如式(2)所示;第1个约束表示毁伤门限［3］以保证分配方案π对目标的最低杀伤;KRj表示第j个目标的毁伤门限，可根据战场态势等具体任务需要由指挥员制定;第2个约束表示每枚导弹只能攻击1个目标.

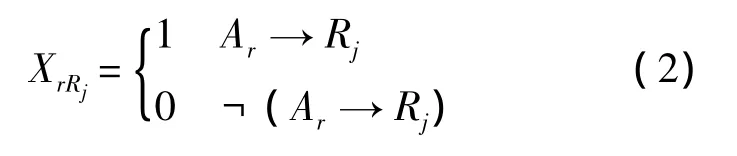
2 进化多目标优化算法

2.1 多目标决策理论

多目标优化问题(MOPs)指目标函数多于1个且需同时处理的问题.多目标决策与单目标决策最大的不同在于解的寻优用Pareto占优进行度量，即“支配”关系，会同时存在多个Pareto非支配解，构成 Pareto最优解集(Pareto-optimal set)［4］.为便于后续讨论给出定义如下.

定义1 Pareto占优.πA，πB∈Ω 是所求多目标函数的两个可行解，称与πB相比，πA是Pareto占优的，当且仅当

定义2 Pareto最优解.一个解π*∈Ω被称为Pareto最优解，当且仅当

Pareto最优解的集合为Pareto最优解集P*.

定义3 Pareto前沿.Pareto最优解集 P*中的解对应目标值组成的曲面称为 Pareto前沿F*:

2.2 进化多目标优化算法

进化多目标优化(EMO)通过在代与代之间维持由潜在解组成的种群来实现全局搜索.这种方法对于搜索Pareto最优解集是非常有效的，一些新颖的多目标优化算法相继提出［7］.

EMO用基于支配关系的比较机制评价解的优劣，Pareto最优解集需设置一个外部种群保存.此类问题不仅要考虑解的收敛性，还要考虑解分布的均匀性，以保证解的多样性，一般用自适应网格机制［4］，将外部种群按照目标函数空间均匀地划分为网格.在删除个体时，含有较多个体的网格中的粒子赋予较高选中概率;在选取个体作为进化种群的全局最优时，含有较少个体的网格中粒子赋予较高概率，基于转盘赌方式进行选择.

3 基于MODPSO-GSA的模型求解

文中分别采用多目标离散粒子群优化(MODPSO)、多目标引力搜索算法(MOGSA)及多目标离散粒子群-引力搜索算法MODPSO-GSA实现WTA模型求解.

3.1 基于MODPSO的模型求解

求解WTA问题的单目标离散粒子群(DPSO)算法可参见文献［3，8-9］.在具体 WTA问题上，MODPSO用粒子位置代表一组分配方案，粒子位置矢量为 X=［X1，X2，…，XK］，K 为待分配导弹数量;粒子速度矢量为 V=［v1，v2，…，vK］.粒子按式(6)更新速度及位置:

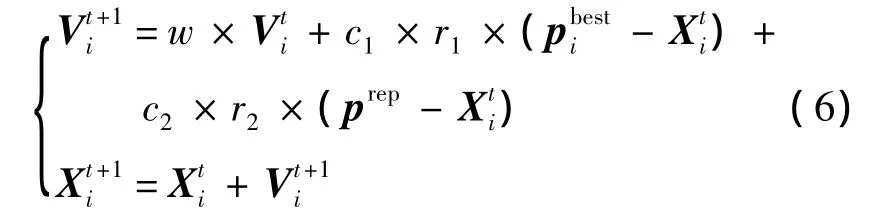
式中，t为迭代次数;c1和c2为学习因子;r1和r2为(0，1)之间的随机数;w为惯性权重;pbesti为粒子i搜索到的最优位置;prep为基于转盘赌从外部种群选取的Pareto占优解来引导寻优.

3.2 基于MOGSA的模型求解

引力搜索算法(GSA)是一种基于万有引力定律寻优的智能优化算法，算法将每个可能解视为在空间中有质量的个体，质量越大代表越优的位置，个体之间基于牛顿定律，通过万有引力作用相互吸引产生运动，引导群体向最优解区域搜索［10］.图1给出了 M2，M3，M4均对 M1产生引力作用.

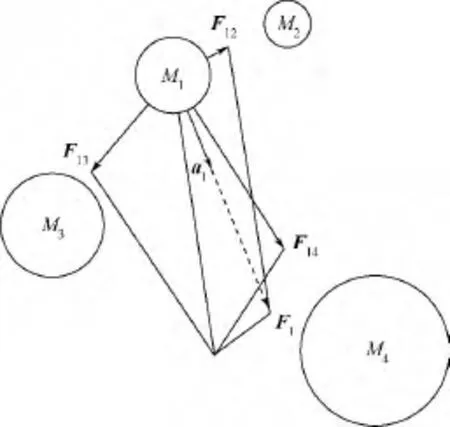
图1 个体之间引力相互作用构造合力F1Fig.1 Resultant force F1from other masses

GSA具有良好的全局寻优能力［11-13］，尚未应用在WTA问题.此处对GSA简略介绍，可参见文献［10］.单目标GSA主要步骤如下:

1)初始化.由N个个体组成搜索群体，搜索空间为K维，个体i位置定义为

2)计算个体质量Mi(t).

3)计算个体j对个体i的引力Fij(t).

4)计算个体j对个体i的引力加速度aij(t).

其中，Xi表示个体i的位置;Rij(t)表示Xi与Xj之间的欧式距离;ε表示最小门限，防止分母为0;G(t)表示此时的引力常数，以控制迭代步长.

5)根据牛顿运动定律，计算合力加速度如式(9)所示，控制变量Kbest随时间递减，表示只有前Kbest个适应值最好的个体产生引力，控制算法收敛到最优解;randj为随机数.个体的速度及位置更新如式(10)所示.

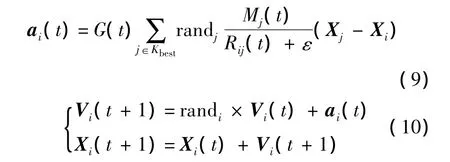
6)若没达到迭代次数，转步骤2);否则停止计算.

MOGSA多目标优化改进采用基于支配关系的比较机制和基于自适应网格的外部种群.主要是如何在两个目标函数与个体单一质量之间建立对应关系，此处参考NSGA-II根据个体间非支配关系为个体分级［14］来定义个体质量:定义不被其他个体支配的个体集合rank=1，只被一个个体支配的个体集合定义rank=2，以此类推.如下所示为非支配关系分级伪代码，其中rank=1的个体集合就是Pareto最优解.

对于进化种群中的粒子p定义集合DomSetp存放被该粒子支配的粒子，变量DomedNump记录该粒子被支配的次数.如果一个粒子被支配次数为0，则该粒子 rankp=1，该粒子集合记为 S1.对于第i等级的粒子集合Si中的粒子p，它所支配的粒子集合DomSetp中的每个粒子q的Domed-Numq减1后DomedNumq=0，则说明q只被粒子p支配，粒子q等级为i+1，存入i+1等级的粒子集合Fi+1，以此类推完成非支配分级.

3.3 基于MODPSO-GSA的模型求解

MODPSO收敛速度快，但易早熟收敛;MOGSA表现出良好的求解空间探索(exploration)能力，但缺乏有效加速机制［13］.文中将二者结合，用一种协同进化的形式［15］:将PSO算法速度更新中的“社会(social)部分”(即gbest)与GSA的加速度结合起来，混合算法的速度更新如式(11)所示.

式中，ai(t)表示MOGSA构造的加速度;VMax表示粒子速度限定;XMin，XMax分别表示位置的最大最小限定;其余变量与式(6)中变量意义相同.

在迭代过程中可能会产生“非法”个体，如分配中遗漏敌机或分配过多导弹攻击同一目标.算法中引入局部调整adjustX:对分配方案中超过杀伤概率的目标尝试删除冗余分配;对于未达到毁伤概率的目标尽量弥补，从未分配导弹中选择对于该目标毁伤概率最大的导弹分配给该目标.MOPSOGSA算法结构流程如图2所示.

图2 MODPSOGSA算法流程图Fig.2 Procedure of MOPSOGSA

4 算例仿真及分析

为验证模型及求解算法有效性，采用文献［3］中算例进行仿真，我方编队由4架战机组成，每架战机挂载4枚导弹;敌机编队由10架飞机组成.各目标的毁伤概率门限可由指挥员进行设定，仿真中KRj均设为0.9.敌机的威胁权重矩阵dRB=［0.6，0.7，0.3，0.5，0.6，0.35，0.65，0.55，0.4，0.75］.经评估我导弹对目标的毁伤概率矩阵［3］如式(12)所示.

仿真时用文中提出的WTA模型建模，并同时用 NSGA-II［16］，MODPSO，MOGSA 及 MODPSOGSA这4种算法对该算例进行求解.进化种群规模均设置为60，迭代次数为100.NSGA-II中进化种群与外部种群是合一的，采用二元竞赛图选择算子，交叉概率 Pc=0.8，变异概率 Pm=0.3;MODPSO，MOGSA，MODPSO-GSA的外部种群设置数量门限为10，网格设置为10×10.MODPSO中基本单目标参数设置参见文献［3］，MODPSOGSA采用MODPSO和MOGSA中的参数设置.

仿真结果如图3所示，横坐标E(π)表示目标函数1;纵坐标N(π)表示目标函数2，直线为各算法寻到的Pareto最优解.NSGA-II收敛于寻到的Pareto最优解集;MODPSO寻到的Pareto最优解如图中连线所示，进化种群如图中点集所示;MOGSA迭代后基本收敛到Pareto最优解集;MODPSO-GSA寻到的Pareto最优解集如图中连线所示，进化种群多样性仍较好.由图可知，MODPSO-GSA具备较好的寻优能力且粒子多样性得到了保持.4种算法寻到的Pareto最优解比较如图 4所示，MODPSO-GSA具备最佳寻优性能.

图3 4种算法迭代结束状态Fig.3 Last states of four algorithms

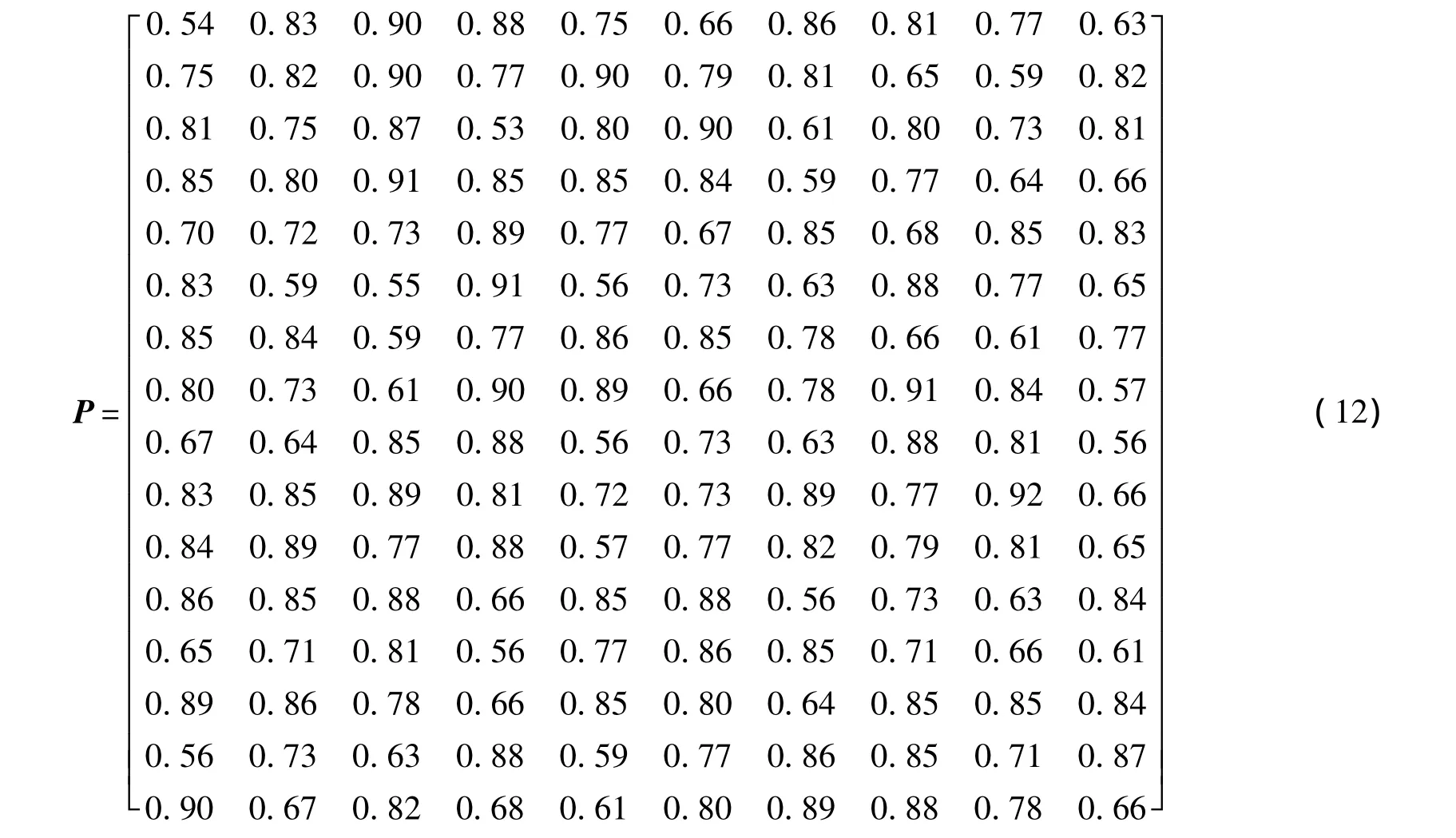
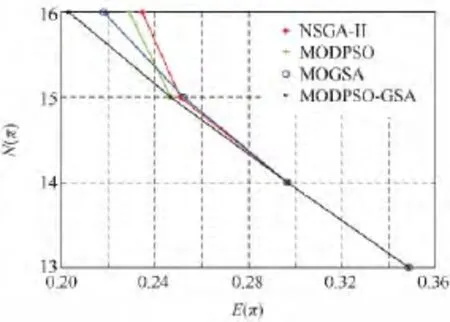
图4 4种算法迭代结果比较Fig.4 Overall results of four algorithms

仿真可知:①耗弹量为13和14的分配方案是每种多目标优化算法都能寻到的稳定分配，也是其他WTA 算法［1，3］寻到的最优分配，证明了多目标优化的有效性;②多目标优化算法可一次运行寻得不同耗弹量下的多个最优目标分配方案，达到预设的目标毁伤概率，指挥员可根据空战态势进行分配方案优选，这更符合空战实际情况;③MODPSO-GSA保持了粒子群算法的快速寻优能力，寻优性能是稳定的并优于其他算法.

图5是MODPSO-GSA寻到的4个分配方案及达到的毁伤效果，图中标示了每个分配方案的敌总期望剩余威胁和我方用弹量.4种方案均是可行分配，指挥员可根据不同的战场态势进行决策.

4种多目标优化算法各运行20次取平均性能如表1所示，MODPSO-GSA具备相对最好的综合性能.

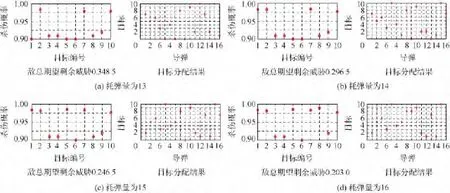
图5 不同耗弹量下的毁伤效果及分配方案Fig.5 Killing probability and weapon-target assignment(WTA)for varied missiles used

表1 平均性能对比Table1 Comparison of average performance

5 结论

1)构建多目标决策模型，选取对敌杀伤效果最大和消耗火力资源最小作为决策目标，提出新的目标分配模型，模型具备直观性.

2)提出基于混合离散粒子群-引力搜索的多目标优化算法求解所建多目标决策模型，展现了良好的寻优能力.

3)进化多目标优化的优势在于一次运行可得到多个Pareto最优解，在文中模型可在满足毁伤门限的前提下，寻到多个不同耗弹量下的最优分配方案，指挥员可根据不同空战态势决策优先，具备实战意义.

4)文中所提多目标优化算法属集中式WTA方式，对通信及指控中心依赖性强，当空战态势剧烈变化或通信质量难以保证时仍有待改进.

References)

［1］ 刘传波，邱志明，吴玲，等.动态武器目标分配问题的研究现状与展望［J］.电光与控制，2010，17(11):43-47.Liu C B，Qiu Z M，Wu L，et al.Review on current status and prospect of researches on dynamic weapon target assignment［J］.Electronics Optics ＆ Control，2010，17(11):43-47(in Chinese).

［2］ 陈闽.编队协同作战目标分配建模综述［J］.电光与控制，2013，20(9):53-63.Chin M.A survey on modeling of target allocation for formation cooperative combat［J］.Electronics Optics ＆ Control，2013，20(9):53-63(in Chinese).

［3］ 李俨，董玉娜.基于SA-DPSO混合优化算法的协同空战火力分配［J］.航空学报，2010，31(3):626-631.Li Y，Dong Y N.Weapon-target assignment based on simulated annealing and discrete particle swarm optimization in cooperative air combat［J］.Acta Aeronautica et Astronautica Sinca，2010，31(3):626-631(in Chinese).

［4］ 公茂果，焦李成，杨咚咚，等.进化多目标优化算法研究［J］.软件学报，2009，20(2):271-289.Gong M G，Jiao L C，Yang D D，et al.Evolutionary multi-objective optimization algorithms［J］.Journal of Software，2009，20(2):271-289(in Chinese).

［5］ 岳超源.决策理论与方法［M］.北京:科学出版社，2006:151-169.Yue C Y.Decision theory and methods［M］.Beijing:Science Press，2006:151-169(in Chinese).

［6］ 段海滨.蚁群算法原理及其应用［M］.北京:科学出版社，2006:312-317.Duan H B.Ant colony algorithms:theory and applications［M］.Beijing:Science Press，2006:312-317(in Chinese).

［7］ Coello C C，Veldhuizen V D，Lamont G.Evolutionary algorithms for solving multi-objective problems［M］.2nd ed.New York:Springer-Verlag，2007:1-10.

［8］ 段海滨，张翔银，徐春芳.仿生智能计算［M］.北京:科学出版社，2011:63-85.Duan H B，Zhang X Y，Xu C F.Bio-inspired computing［M］.Beijing:Science Press，2011:63-85(in Chinese).

［9］ 郭文忠，陈国龙.离散粒子群优化算法及其应用［M］.北京:清华大学出版社，2012:13-16.Guo W Z，Chen G L.Discrete particle swarm optimization algorithm and its application［M］.Beijing:Tsinghua University Press，2012:13-16(in Chinese).

［10］ Esmat R，Hossein N，Saeid S.GSA:a gravitational search algorithm［J］.Information Sciences，2009，179(13):2232-2248.

［11］ 杨晶，黎放，狄鹏.免疫万有引力搜索算法的研究与仿真［J］.兵工学报，2012，33(12):1533-1538.Yang J，Li F，Di P.Research and simulation for the gravitational search algorithms with immunity［J］.Acta Armamentarh，2012，33(12):1533-1538(in Chinese).

［12］ 谷文祥，李向涛，朱磊，等.求解流水线调度问题的万有引力搜索算法［J］.智能系统学报，2010，5(5):411-418.Gu W X，Li X T，Zhu L，et al.A gravitational search algorithm for flow shop scheduling［J］.CAAI Transactions on Intelligent Systems，2010，5(5):411-418(in Chinese).

［13］ 李沛，段海滨.基于改进万有引力搜索算法的无人机航路规划［J］.中国科学:技术科学，2012，42(10):1130-1136.Li P，Duan H B.Path planning of unmanned aerial vehicle based on improved gravitational search algorithm［J］.Scientia Sinica Technologica，2012，42(10):1130-1136(in Chinese).

［14］ Hadi N，Mahdi N，Patrick S.A multi-objective gravitational search algorithm based on non-dominated sorting［J］.International Journal of Swarm Intelligence Research，2012，3(3):32-49.

［15］ Seyedali M，Siti Z M H.A new hybrid PSOGSA algorithm for function optimization［C］//International Conference on Computer and Information Application.Piscataway，NJ:IEEE，2010:374-377.

［16］ Kalyanmoy D，Amrit P，Sameer A，et al.A fast elitist multi-objective genetic algorithm:NSGA-II［J］.IEEE Transactions on Evolutionary Computation，2002，6(2):182-197.