关于闭环供应链废旧品回收分级定价策略研究

洪 佳，李 芳 （上海理工大学 管理学院，上海200093）

HONG Jia, LI Fang (School of Management, University of Shanghai for Science & Technology, Shanghai 200093, China)

0 引 言

市场经济的快速发展使得制造商不断推陈出新，产品更新换代的速度不断加快，大量产品在使用寿命未终结时便遭淘汰，给社会带来了巨大的资源浪费。然而，近年来随着地球上不可再生资源的日益枯竭，传统经济不断向循环经济发展，人们的环保意识不断增强，对可持续发展的认识不断深入，世界各国纷纷加强了对环境保护的立法，废弃产品的回收再制造也越来越受到人们的重视，闭环供应链成为学术界关注的热点问题。

关于再制造的回收定价策略是闭环供应链研究的难点之一。逆向供应链与传统供应链的运作机制截然不同，传统的供应链定价策略在闭环供应链中不再适用，因此闭环供应链的实施仍需要通过大量理论指导以及实践探索，才能使之达到平稳运营的状态[1]。

回收处理后再制造品定价策略的复杂性主要体现在：若定价过高，由于产品核心组件及各零部件在使用过后存在磨损，其质量本身必定存在一定的缺陷，生产厂商需要花费更多的资源用于维修和再制造生产，使得生产成本过高，从而影响生产厂商的收益；若定价过低，将无法从市场上回收到足够数量的废旧品，制造厂商无法大量使用价格低廉的废旧品从事再制造生产，需要重新大量购买新的原材料，不利于整个闭环供应链的发展，造成资源的极大浪费，阻碍我国经济的可持续发展[2]。所以，研究废旧品的回收定价策略对闭环供应链的发展至关重要。

综观已有的文献，其研究均假设回收的废品质量单一，并且假定了统一的回收价格，显然这一假设与实际情况不符。因为消费者在使用过程中，会造成产品的核心组件以及各个零部件不同程度的磨损和折旧，故回收的废旧品在质量上也势必存在差异。本文在前人研究的基础上，考虑包含多种质量等级的废品回收，寻求不同质量等级下最优的回收价格策略，以期对我国闭环供应链的发展起到指导作用，推进我国循环经济的发展。

1 问题描述与假设

闭环供应链有三种回收模式，零售商回收模式（MRCRM）、制造商回收模式（MRCM）、第三方回收模式（MRCTM）[3]，而Savaskan R C、Bhattacharya S 等人研究表明：从确定的线性需求出发，比较闭环供应链中三种不同回收渠道的效率，结果表明零售商回收模式是最有效的回收模式[4]。鉴于此，本文选择零售商回收模式的闭环供应链为研究对象，把制造商和零售商的回收价格作为决策变量，并假设不同零售商的回收模式与成本结构相同，简化模型只考虑单个零售商和单个制造商的情况[5]。

国外学者Thierry M.C.等人将零售商回收的旧品依据重新利用的方式不同分为三类：直接再利用、修理再利用、再生再制造[6]。鉴于此，本文假设在消费者使用过后，零售商根据废品的磨损情况，将废品的质量分为A、B、C三个等级，其中A类品为优品，B类品为良品，C类品为中等品，生产厂商对这三类品的再制造过程中所花费的成本不同，其中C类品所花费的成本最多，B类品次之，A类品再制造过程所花费的成本最小。

图1 闭环供应链废品回收再造示意图

2 模型构建

2.1 模型描述

结合图1 对本文的模型构建思路进行简单描述：

如图1 所示，制造商对商品定价为P，零售商以P价格进行批发，零售商再将商品分销给消费者，此过程为正向供应链部分，即商品的销售通道。在消费者使用过后，商品变为废旧品，零售商根据磨损情况，将其质量分为A、B、C三个等级，三类品均可用于再制造，但它们用于再制造的生产成本不同。对于A类的优品，制造商将其用于再制造的单位边际生产成本为Cm；对于B类品，其单位边际再生成本为L1Cm；对于C类品，其单位边际再生成本为L2Cm（其中，L2＞L1＞1）。零售商在回收A、B、C三类废品时，分别以Pa、Pb、Pc的价格从消费者处进行回收；制造商再以PA、PB、PC的价格从零售商处进行回收用于再制造，此过程为逆向供应链部分，即商品的回收通道。

假设Q为整个市场废旧品的拥有量，其中a、b、c分别为市场中A类品、B类品和C类品占整个废旧品市场的比例，则三参数必满足条件：a+b+c=1。通过参考王玉燕等人的研究[7]，可将零售商对三类旧品的回收量XA、XB、XC分别定义为关于单位旧品回收价格的函数，则三类旧品的回收量分别如下：

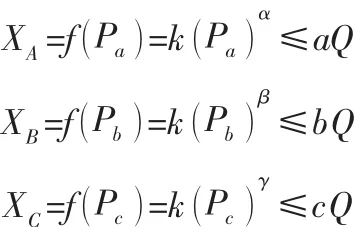
其中α、β、γ 分别为三类旧品的价格弹性参数，且α, β, γ∈[0,1]；k为换算常数。用φ 表示政府制定的相关环境保护法所规定的废旧品回收比例，则必须满足XA+XB+XC≥φQ，则XC需满足φQ-XA-XB≤XC≤（1-a-b）Q。零售商再以PA、PB、PC的价格回销给制造商，零售商的单位边际运营成本为Cr。

πm、πr、π 分别表示制造商、零售商以及整个闭环供应量系统的利润，其中π=πm+πr。

本文进行模型构建时采用的参数及其含义均与上述一致。

2.2 基本假设

本文建立的关于废旧品回收的分级定价回收模型基本假设如下：

假设1：不同零售商的回收模式与成本结构相同，可以将模型简化，只考虑单个零售商和单个制造商的情况；

假设2：利用三类旧品的单位再造成本小于新产品的单位制造成本C，即Cm ＜L1Cm ＜L2Cm ＜C，表示制造商利用回收的废旧品制造商品是有利可图的，否则制造商回收废旧品毫无意义；

假设3：模型中闭环供应链的决策是单期的；

假设4：闭环供应链中成员的决策方式为完全信息下非合作二阶段斯坦博格博弈模型[8]。

2.3 闭环供应链分级定价回收模型的构建

根据上述闭环供应链的废品回收模式、设置的参数以及基本假设，建立闭环供应链分级定价回收模型。从整个闭环供应链废旧品回收再造的流程示意图来看，制造商、零售商以及整个闭环供应链的收益分别如下：

3 模型解析

3.1 分散定价决策

分散定价决策，即决策双方均以各自的利润最大化为目标，如上假设，决策双方制造商和零售商构成了完全信息下非合作二阶段斯坦博格博弈模型，即Stackelberg 主从博弈模型，此时制造商为领导者，零售商为追随者，制造商首先制定自己的批发价格P和对零售商的三类旧品回收价格PA、PB、PC，以使自己的收益最大化；然后零售商根据制造商的价格策略来确定自己的市场回收价格Pa、Pb、Pc，依据逆向归纳法对模型进行两阶段求解[9]，可得制造商对零售商三类旧的最优品回收价格，如下：

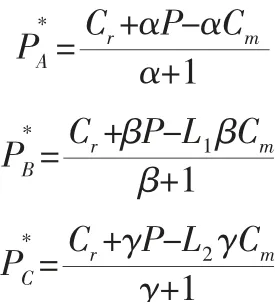
3.2 联合定价决策

在联合定价策略模型中，可以将整个闭环供应链看作是一个集成式的“超组织”结构，闭环供应链上制造商与零售商通过协商合作共同确定三类废旧品的市场回收价格Pa、Pb、Pc，并假设在此条件下，闭环供应链的系统利润为：

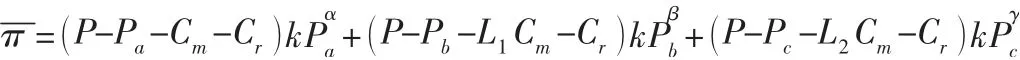
其中，上标“—”表示在联合定价的策略下，同下文。将上式中π 分别对Pa、Pb、Pc求偏导后，再求上式的最大值，可得：综上所述，对分散决策下和联合定价决策下的闭环供应链系统利润进行比较，易证：

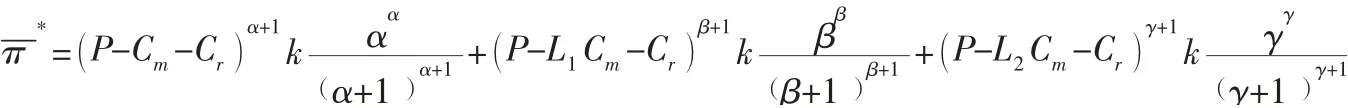
通过上述的证明可知：制造商和零售商通过合作进行联合定价时，整个闭环供应链系统将会获得更高的收益。

4 算例分析

本节欲通过算例分析来验证两种决策模式下的最优定价策略以及各决策主体的收益。假定某种产品的价格服从正态分布，即P～N（700,50），其他参数α=0.82, β=0.67, γ=0.51,k=1.34,Cm=150,Cr=30,L1=1.5,L2=2,r=0.75，由于目前国内还尚未颁布相关的环境保护法令，因此令φ=0。利用MATLAB7.0 对模型进行数值仿真，可确定模型中各决策变量的数值，并分析比较各数值的大小，得表1 如下：

表1 不同决策模式下各决策变量的最优解及其比较

通过表1 中各参数的比较可知：联合定价的决策模型明显优于分散定价决策模型，可使制造商和零售商的收益都增加。假使整个供应链的成员都是理性的经济人，追求各自的利益最大化，制造商和零售商都将选择联合定价决策模型。

5 结论与展望

本文运用博弈论的思想方法建立数学模型，求解出闭环供应链中的博弈双方分别在分散决策和联合定价决策下各自的最优定价策略，并分别对模型进行数值仿真，得出主要结论为：采取联合定价策略时，整个闭环供应链的系统利润更高，且博弈双方的利润都显著提高，显然联合定价的策略优于分散决策的定价策略；在联合定价的策略下，零售商的市场回收价格明显高于分散决策情况下的市场回收价格，根据三类旧品回收量XA、XB、XC分别是关于单位废旧品回收价格的函数可知，三类旧品回收量都将提高，这说明在联合定价的策略将带来更好的节能环保效益，有利于我国循环经济和环保事业的发展。

[1] 王玉燕，李帮义，申亮. 供应链、逆向供应链系统的定价策略模型[J]. 中国管理科学，2006,14(4):40-45.

[2] 葛静燕，黄培清. 基于博弈论的闭环供应链定价策略分析[J]. 系统工程学报，2008,23(1):111-115.

[3] Savaskan R.C., Bhattachary S., Van Wassenhovc L.N.. Channel choice and Coordination in a Remanufacturing Environment[Z].Working Paper, 1999.

[4] Savaskan R C, Bhattacharya S, Wassenhove L N V. Closed-loop Supply Chain Models with Product Remanufacturing[J].Management Science, 2004,50(2):239-252.

[5] Savaskan R C, Wassenhove L N V. Reverse Channel Design: The Case of Competing Retailers[J]. Management Science,2006,52(1):1-14.

[6] Thierry M.C., Salomon M., Van Nunen J.. Van Wassenhovc L Strategic Issuses in Product Recovery Management[J]. California Management Review, 1995,37(2):114-135.

[7] 王玉燕，李帮义，乐菲菲. 两个闭环供应链的定价模型研究[J]. 预测，2006(6):70-73.

[8] Cachon G.P. Supply Chain Coordination with Contracts[Z]. Working Paper, 2003.

[9] 林欣怡，孙浩，达庆利. 随机环境下再制造产品的定价策略研究[J]. 运筹与管理，2012(6):149-153.

[10] 王巍. 闭环供应链分级定价回收策略研究[J]. 统计与决策，2010(5):174-176.