设备随机故障条件下的经济生产批量模型
方潇珞,吕文元 FANG Xiao-luo, LV Wen-yuan
(上海理工大学 管理学院,上海200093)
(Management School, University of Shanghai for Science and Technology, Shanghai 200093, China)
0 引 言
经典的经济生产批量(Economic Manufacture Quantity, EMQ) 模型通常简单地默认生产过程一直完好,设备运行可靠,生产的产品均为合格产品。但是,实际情况并非如此理想。考虑到经典的EMQ 模型已与复杂的生产状况相去甚远,许多学者从客观实际出发丰富了EMQ 的拓展研究。
主要研究方向有三点:其一,由于设备的磨损使得生产过程可能由受控状态转变为失控状态,在失控状态下生产出一定比例缺陷产品。Porteus[1]最早认识到生产过程可能发生劣化,进而生产出一定比例缺陷产品,研究发现小批量生产更经济;同年,Rosenblatt 和Lee[2]做了类似研究,结论是该模型下的最优生产时间比经典EMQ 模型里的短;Lee 和Rosenblatt[3]假定生产过程劣化发生时间服从指数分布,考虑了对劣化生产系统的检修,发现最优的检查间隔期是相等的,给出了最优生产时间和检查策略;在文献[3]的基础上,Lee 和Park[4]认为缺陷产品的售前返修费用明显小于售后保修费用,通过考虑两者的差异,研究了劣化生产系统的生产计划和检查策略的联合优化问题;Hariga 和Ben-Daya[5]放宽了文献[2]中劣化发生时间服从指数分布的假设条件,研究了生产过程劣化发生时间服从任意分布的EMQ 模型,推导出最小费用的自由边界分布;Kim 和Hong[6]假设检查只在生产结束后而不是在生产过程中进行;Wang[7]基于文献[6]的检查策略假设,指出当把失控状态的生产系统修复到受控状态所需的费用大于缺陷产品的费用时,文献[2]模型中的最优生产时间未必总是比经典EMQ 模型的短。其二,设备可能发生随机故障,迫使生产中止,影响严重。Groenevelt 等[8]首次在EMQ 模型中考虑设备随机故障的影响因素,发现经济批量变大且随着故障率的增加而增加;随后,他们[9]引入安全库存,修正了文献[8]的EMQ 模型;Makis 和Fung[10]研究了缺陷产品和设备故障对最优生产批量和检查次数的影响;Chakraborty 等[11]对比研究了生产过程劣化和设备随机故障共同影响下两种检查策略的最优生产批量;潘尔顺和李庆国[12]改进了田口损失函数,建立了含返修和质量损失成本的EMQ 模型;吕文元和化彬[13]考虑了设备故障维修时间,研究了允许缺货的EMQ 模型的生产计划和检查策略的联合优化问题。其三,产品质量通常是衡量生产过程状态的标准,但是Dorris 和Foote[14]研究发现由于检验员和仪器的原因,检查错误是存在的,影响生产过程状态的判断和产品的质量,有必要考虑检查错误对EMQ 模型的影响。检查错误分为两类:第Ⅰ类检查错误是指把受控状态的生产过程判定为失控状态,误判的合格产品重新进行修复;第Ⅱ类检查错误是指实际处于失控状态的生产过程没有被检测出,漏判的缺陷产品流入市场。Liou 等[15]和Makis[16]认为两类检查错误会严重影响产品质量,故将其引入EMQ 模型,修正了文献[3]的模型;Yoo 等[17]从企业利润最大化的角度,研究了两类检查错误共同影响下的EMQ 模型。
基于以上文献,本文综合考虑生产计划、设备维修和质量控制三个方面,改进并建立更切合实际的EMQ 模型,研究了生产过程劣化、设备随机故障及第Ⅱ类检查错误共同影响下的生产计划和检查策略的联合优化问题,目的是求得使单位时间内总费用期望值最低的最优经济生产批量和检查次数,为企业生产管理提供更有效的指导。
1 问题描述

图1 每生产周期的生产—库存状态
本文所描述的生产系统与经典的EMQ 模型所描述的有相同之处又有其不同。首先是相同点:生产从库存为0 时开始进行,经过生产时间Q/p结束。由于生产率p大于需求率d,所以库存以p-()d速率上升。在Q/p时,批量Q生产完成,库存达到峰值,生产停止,库存随着需求率d开始下降。当库存再次减少到0 时,开始下一次的生产,如此循环。与经典的EMQ 模型的不同点如下:
(1) 经典的EMQ 模型假设生产过程一直完好,生产的都是合格产品,但在实际生产中,由于设备不断受到磨损,致使生产过程发生劣化,缺陷产品的出现不可避免。本文所描述的生产系统在每次生产开始时,生产过程都处于受控状态,生产的产品均合格。在运行一段时间τ 后,生产过程可能转变为失控状态,如图1 中“·”所示,此时开始生产出一定比例的缺陷产品。为了减少缺陷产品带来的损失,在生产运行期间,对生产过程进行定期检查,定期检查如图1 中“▍”所示,检查次数为n,在没有发生设备故障的生产周期中,第n次检查在生产结束时进行来保证下一生产周期开始时设备处于受控状态。一旦检查发现生产过程处于失控状态,立即对其进行修复,即生产过程重新回到受控状态,并对缺陷产品进行返修。
(2) 产品质量通常是衡量生产过程状态的标准,但由于检验员和仪器的原因,检查错误是客观存在的,检查错误分为两类:第Ⅰ类检查错误是指把受控状态的生产过程判定为失控状态,误判的合格产品重新进行修复;第Ⅱ类检查错误是指实际处于失控状态的生产过程没有被检测出,漏判的缺陷产品直接流入市场。本文考虑第Ⅱ类检查错误的影响,部分缺陷产品没有得到售前返修直接进入市场,以次充好的情况引起客户抱怨,从而产生相应的缺陷产品的售后保修费用。
(3) 设备严重磨损直接导致故障停机,设备故障是随机发生的,一旦发生故障,生产停止,并对其进行事后维修。因此,本文的假定条件如下:
(1) 考虑单台生产设备上单一产品的单周期生产过程。
(2) 产品生产率p和产品需求率d为常量,且p>d,生产是间歇的,需求是持续的。
(3) 生产过程劣化与生产系统随机发生故障相互独立。一般说来,生产过程劣化和设备随机发生故障是相关的,由于对生产过程经常检查,可以及时纠正生产过程的失控状态,因此假定二者相互独立是合理的。
(4) 检查时间和检查修复时间与生产运行时间相比可以忽略不计。
(5) 生产过程经过一个随机时间τ 从受控状态变为失控状态,假定τ 服从参数为λc的指数分布。
(6) 被检查出来的缺陷产品进行返修可再次投入消耗使用,在考虑第Ⅱ类检查错误的情况下,有一定比例的缺陷产品被漏判,没有得到返修而直接通过销售进入市场,这部分缺陷产品会引起一笔售后保修费用。
(7) 生产系统空闲时,不发生劣化和故障。
根据以上描述和假设,该生产系统内的总费用一共包括六项:生产准备费用、库存费用、生产过程的检查费用、劣化生产过程的修复费用、缺陷产品的返修费用及保修费用、故障维修费用。研究的目的是通过建立模型找到满足单位时间内总费用期望值TC*最低的最优生产批量Q*以及最优检查次数n*。
2 模型建立
2.1 符号假设
d:需求率(个/天);
p:生产率(p>d,个/天);
Q:生产批量(个);
Cs:每次生产准备费用(元/次);
h:单位产品单位时间的库存费用(元/个/天);
Cd:单位缺陷产品的售前返修费用(元/个);
Cw:单位缺陷产品的售后保修费用(元/个);
α:失控状态时,生产缺陷产品的比例(%);
β:第Ⅱ类检查错误率(%);
Ci:每次检查费用(元/次);
Cr:失控生产过程的修复费用(元/次);
Cf:故障维修费用(元/次);
n:每生产周期的检查次数(次);
τ:在每次检修后生产过程由受控状态转变到失控状态所经历的时间(天);
m:相邻两个检查间隔期内生产缺陷产品数量(个);
mf:设备发生故障的检查间隔期内生产的缺陷产品数量(个);
t:故障发生前,总的生产运行时间(天);
Fd(t) :t的分布函数;
fd(t):t的概率密度函数。
2.2 建立模型
对于设备发生故障的生产周期,生产运行时间为t,生产周期的长度为pt/d。生产系统内的总费用一共包括六项:生产准备费用、库存费用、生产过程的检查费用、劣化生产过程的修复费用、缺陷产品的返修费用及保修费用、故障维修费用。各项费用如下列公式所示:
每生产周期的生产准备费用为:

每生产周期的库存费用的期望值为:

故障发生前,已进行的检查次数为「npt/Q」,则每生产周期的检查费用的期望值为:

假定生产过程由受控状态转变到失控状态的时间即劣化率服从参数为λc的指数分布,则每个生产检查间隔期的修复费用的期望值为:

所以,每生产周期的缺陷生产过程的修复费用的期望值为:

假设设备发生故障的生产检查间隔期的生产运行时间为Tf,则有:

设备发生故障前的每个生产检查间隔期所生产的缺陷产品数量的期望值为:

所以,设备发生故障的生产检查间隔期所生产的缺陷产品数量的期望值为:

考虑第Ⅱ类检查错误率β,即缺陷产品漏判的概率为β,那么:

所以,由式(7)、式(8)、式(9) 可得每生产周期所生产的缺陷产品的返修及保修费用的期望值为:

每生产周期的故障维修费用为:

在一个生产周期中,如果设备没有发生故障,那么生产运行时间为Q/p,周期长度为Q/d。则生产周期内各项费用如下列公式所示:
每生产周期的生产准备费用为:

每生产周期的库存费用的期望值为:

每生产周期的检查费用的期望值为:

每生产周期的缺陷生产过程的修复费用的期望值为:

每生产周期的缺陷产品的返修及保修费用的期望值为:

综合上述式(1) 至式(16),每生产周期的总费用的期望值为:
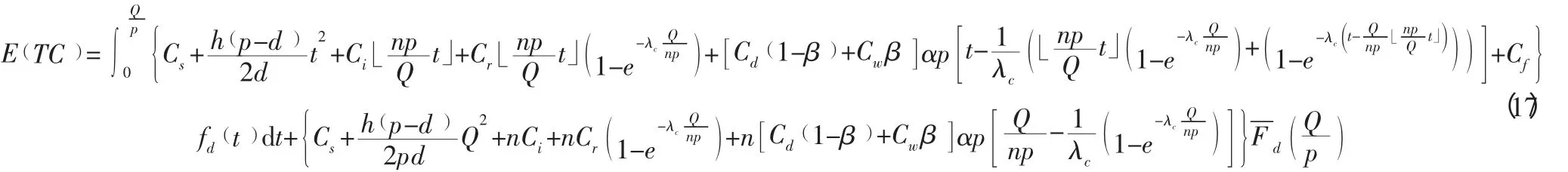
根据定义,每生产周期长度的期望值为:

每生产周期的单位时间内总费用的期望值为:

将式(17) 和式(18) 代入式(19),利用Matlab 等软件以及优化算法,即可以求出满足单位时间内总费用的期望值TC*最低的最优生产批量Q*以及最优检查次数n*。
3 算例分析
应用一个算例来说明本文所建模型的有效性。假设生产过程劣化率、设备故障率分别服从参数为λc、λd的指数分布,具体参数取值如表1 所示:

表1 参数值
将表1 的参数值代入,利用粒子群算法进行求解,其计算结果如表2 所示。
分析计算结果可知:
(1) 当故障率λd和缺陷率λc一定时,单位时间内的总费用期望值TC*伴随着第Ⅱ类检查错误率β 的增大而明显增大,最优检查次数n*也增多。其中原因在于,第Ⅱ类检查错误率β 的上升,意味着更多的缺陷产品没有被检测出来,跳过内部售前返修而直接流向市场,以次充好的情况加剧,引起更多客户抱怨,因此企业需要承担和支付的售后保修费用增加;为了降低第Ⅱ类检查错误率β,一方面除了提高质检人员的技能,更重要的方面是尽可能减少缺陷产品的生产数量,因此投入的检查次数自然增多以保证生产过程尽可能处于受控状态,检查费用增加。由于生产的产品均投入消耗使用,经济生产批量Q*和第Ⅱ类检查错误率β 没有明显的正相关抑或负相关关系,经济生产批量Q*在一定小范围内维持稳定波动。

表2 模型的计算结果
(2) 当故障率λd和第Ⅱ类检查错误率β 一定时,随着缺陷率λc的增加,单位时间内的总费用期望值TC*和最优检查次数n*都呈现正相关变化。其中原因在于,缺陷率λc的上升表明生产过程由受控状态转移到失控状态的可能性变大,生产的缺陷产品数量增多,进而导致更多的缺陷产品的返修和保修费用;为控制生产过程不要转移到失控状态,必然要提高检查次数,检查费用增加以及修复失控状态的生产过程的修复费用增加。由于生产的产品都用于消耗使用,经济生产批量Q*和缺陷率λc没有明显关系,经济生产批量Q*较稳定。
(3) 当缺陷率λc和第Ⅱ类检查错误率β 一定时,随着故障率λd的增加,经济生产批量Q*和单位时间内的总费用期望值TC*也在增加,然而最优检查次数n*基本不变。其中原因在于,故障率λd的上升是指设备发生故障停机的可能性变大,停机的次数增加意味着更多故障维修和设备重启,增加了设备维修费用和生产准备费用;为了减少设备启动次数,就要提高经济生产批量,从而增加了库存费用;当经济生产批量Q*增幅不大时,生产运行时间基本相近,且缺陷率一定,故最优检查次数n*不变,然而当经济生产批量Q*的增幅较大,相应的生产运行时间自然延长,所以,最优检查次数n*小幅增加也在情理之中。
这与实际的生产状况相符,表明了本文模型的有效性。企业一方面要重视检查错误的恶劣影响,严格控制,减少不必要的售后成本,保障企业信誉;另一方面要加强对设备的维护和保养,降低设备的缺陷率和故障率可以有效降低生产成本,帮助企业获得更大收益。
4 结束语
本文研究了生产过程劣化、设备随机故障及第Ⅱ类检查错误共同影响下的不可靠生产系统。通过建立含生产过程劣化、设备随机故障及第Ⅱ类检查错误的定期检查的单周期EMQ 模型,求得使单位时间内总费用期望值最低的最优经济生产批量和检查次数。算例分析的结果是:①随着第Ⅱ类检查错误率β 的上升,单位时间内的总费用期望值TC*明显增加,最优检查次数n*增加,对经济生产批量Q*影响甚微;②随着缺陷率λc的上升,单位时间内的总费用期望值TC*增加,最优检查次数n*增加,经济生产批量Q*未受影响;③随着故障率λd的上升,单位时间内的总费用期望值TC*增加,经济生产批量Q*增加,最优检查次数n*基本不变。
未来还可以考虑检查修复时间、设备更新等因素的影响,有待进一步研究。
[1] Porteus E L. Optimal lot sizing, process quality improvement and setup cost reduction[J]. Operations Research, 1986,34(1):137-144.
[2] Rosenblatt M J, Lee H L. Economic production cycle with imperfect production process[J]. IIE Transactions, 1986,18(1):48-55.
[3] Lee H L, Rosenblatt M J. Simultaneous determination of production cycle and inspection schedules in a production system[J].Management Science, 1987,33(9):1125-1136.
[4] Lee J S, Park K S. Joint determination of production cycle and inspection intervals in a deteriorating production system[J].Journal of the Operational Research Society, 1991,42(9):775-783.
[5] Hariga M, Ben-Daya M. The economic manufacturing lot sizing problem with imperfect manufacturing processes: bounds and optimal solutions[J]. Naval Research Logistics, 1998,45(4):423-433.
[6] Kim C H, Hong Y. An optimal production run length in deteriorating production processes[J]. International Journal of Production Economics, 1999,58:183-189.
[7] Wang C H. Integrated production and product inspection policy[J]. International Journal of Production Economics, 2005,95:123-134.
[8] Groenevelt H, Pintelon L, Seidmann A. Production lot sizing with machine breakdown[J]. Management Science, 1992,38:104-123.
[9] Groenevelt H, Pintelon L, Siedmann A. Production batching with machine breakdown and safety stocks[J]. Operations Research, 1992,40:959-971.
[10] Makis V, Fung J. An EMQ Model with Inspections and Random Machine Failures[J]. The Journal of the Operational Research Society, 1998,49(1):66-76.
[11] Chakraborty T, Giri B C, Chaudhuri K S. Production lot sizing with process deterioration and machine breakdown under inspection schedule[J]. Int J of Management Science, 2007,37:257-271.
[12] 潘尔顺,李庆国. 田口损失函数的改进以及在最佳经济生产批量中应用[J]. 上海交通大学学报,2005,39(7):1119-1122.
[13] 吕文元,化彬. 考虑设备故障维修时间的经济生产批量模型[J]. 计算机集成制造系统,2015,21(5):1309-1314.
[14] Dorris A L, Foote B L. Inspection Errors and Statistical Quality Control: A Survey[J]. AIZE Transactions, 1978,10(2):184-192.
[15] Liou M J, Tseng S T, Lin T M. The effects of inspection errors to the imperfect EMQ model[J]. IIE transactions, 1994,26:42-51.
[16] Makis V. Optimal lot sizing and inspection policy for an EMQ model with imperfect inspections[J]. Naval Research Logistics,1998,45:165-186.
[17] Yoo S H, Kim D S, Park M S. Economic production quantity model with imperfect-quality items, two-way imperfect inspection and sales return[J]. Int J of Production Economics, 2009,121:255-265.

