标校塔信号源抗风扰稳定系统设计与实现

吴 鑫，戴广明，魏忠良，汪磊磊

(南京电子技术研究所高功率事业部，江苏南京 210039)

雷达在使用过程中需要进行高精度的外场标校，用于标校的信号源通常位于数十m甚至几十m高的标校塔顶端。为了建立目标特性与雷达测得的功率之间严格的数学关系［1－3］，需要信号源与雷达之间的相对位置在测试过程中保持不变［4］。但是雷达所在的外场通常较为空旷，容易受到风载荷的扰动，如何抵抗风载荷扰动成为标校精度的关键。

目前抵抗风载荷扰动的普遍做法是将标校塔塔身设计的足够粗壮，然后通过钢丝绳斜拉标校塔来保证信号源在特定风速下偏摆小于理论测试精度需求的最大偏摆。这样的结构设计局限性较大，仅能保证标校塔偏摆小于数十mm甚至几十mm，测量所得的数据仅能满足最低测量需求，并不能如实反映雷达的性能。因此对于高精度外场标校来说，标校塔加钢丝绳斜拉无法完全满足标校精度需求，且外场风扰动情况复杂，需要在现有基础上提出一种更好的稳定信号源的装置来提升精度。本文提出了一种高精度标校塔信号源稳定系统，可有效的在二维方向上稳定标校塔信号源位置。

1 标校塔信号源抗风扰稳定系统设计

标校塔信号源抗风扰稳定系统由二维稳定平台、二维稳定平台驱动控制器、激光跟踪仪、靶球、控制计算机、交换机等组成，二维稳定平台由X轴执行机构、Y轴执行机构及载物台组成，如图1所示。为实现信号源位置稳定，主要在X、Y平面内中修正风载荷造成的偏摆。

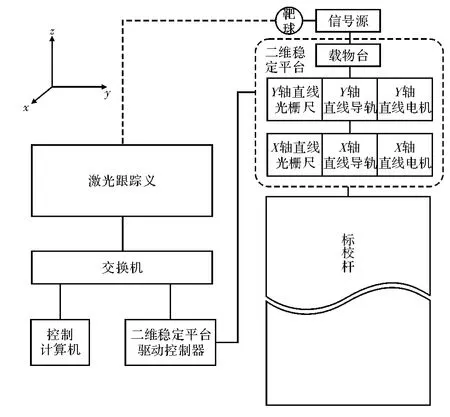
图1 标校塔信号源稳定系统组成

系统按照如下方式进行工作。控制计算机通过交换机和二维稳定平台驱动控制器进行通讯，包括设置电机、光栅尺、闭环参数等。二维稳定平台驱动控制器实时采集直线光栅尺的位置信号，通过驱动直线电机进行位置修正。激光跟踪仪通过交换机往控制计算机发送规定格式的信号，从而反映靶球的实时空间绝对坐标信息。控制计算机通过实时校姿程序计算出该位置坐标和初始位置坐标的差值，然后通过交换机给二维稳定平台驱动控制器发出控制指令。二维稳定平台驱动控制器得到控制指令后驱动直线电机行走相应差值的长度，从而达到修正信号源位置的目的。其中实时校姿程序主要由X轴及Y轴初始寻零、激光跟踪仪与二维稳定平台坐标变换、信号源初始位置采样、信号源实时位置修正等功能组成，如图2所示。

图2 实时校姿程序组成

2 标校塔信号源抗风扰稳定系统

二维稳定系统对信号源的稳定主要依靠激光跟踪仪的实时位置跟踪进行闭环修正，因此将激光跟踪仪的数值用于二维稳定平台闭环控制是该系统最重要的环节。本文就两者之间的关系进行分析，阐述标校塔信号源抗风扰稳定系统的工作原理。

2.1 系统模型简化

抗风扰稳定系统的核心关键仪器是激光跟踪仪，该仪器通过测量两个角度和一个距离来确定目标靶球的坐标。为了得到坐标位置，文中需要进行极坐标与直角坐标的变换。激光跟踪仪示意图如图3所示，其是一种二维框架旋转机构，俯仰角正向定义为Z轴向XY平面旋转方向，方位角正向定义为X轴向Y轴旋转方向。因此通过距离D、俯仰角 θei、方位角 θaz可得到靶球在激光跟踪仪中的坐标(xb，yb，zb)。

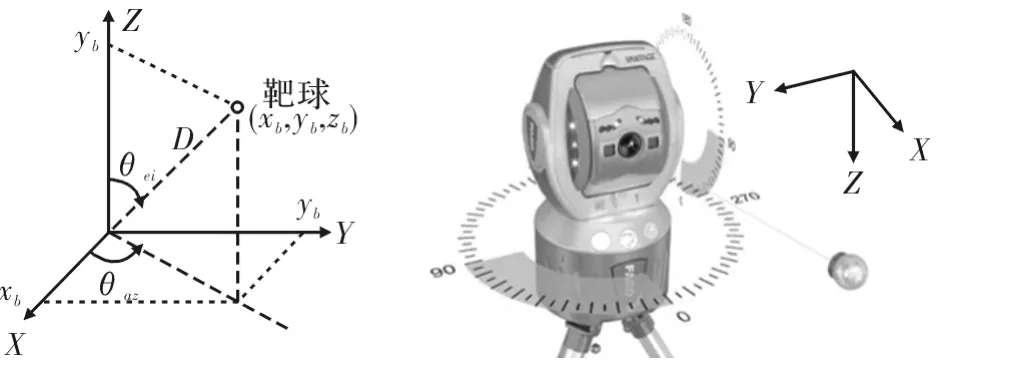
图3 激光跟踪仪测量原理

标校塔高度在十几m甚至几十m的高度，所以对于由于风载荷造成的如图4所示的位移O'W，对应的标校塔偏摆角度θw1，偏摆后W在原坐标系下投影角为θwe1，由于O'W较O'B的长度可忽略，所以角度关系可以近似为

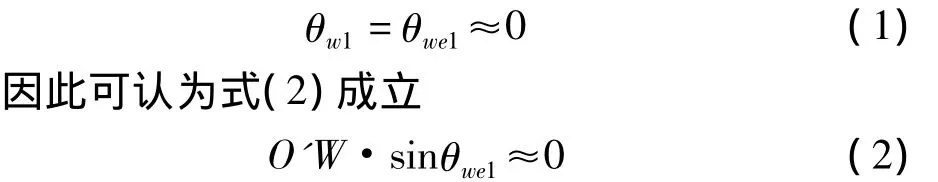
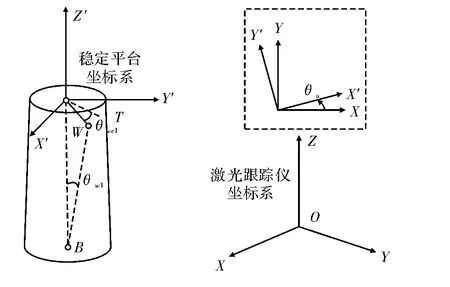
图4 激光跟踪仪与稳定平台坐标关系图

最终可假设风载荷造成的Z轴方向偏移为0，也即假设风载荷造成位移均处于原坐标系X'Y'平面内，将三维平面偏摆问题简化为二维平面问题。因此需要进行的空间变换可以简化为一般的直角坐标变换。

2.2 系统内空间坐标变换

在一般情况下，由旧坐标系O－XY变换成新坐标系O'－X'Y'，共分两步完成，即先移轴使坐标原点与新坐标系的原点O'重合，变成坐标系O'－X″Y″然后再由辅助坐标系 O'－ X″Y″转轴而成新坐标系 O'－ X'Y'［5］。通过坐标变换可得出在二维平台坐标系下靶球的新坐标值。坐标变换需要测得O'在O－XY中坐标值及XY与X'Y'坐标之间的夹角θu，如图4所示。O'在O－XY中坐标值可由激光跟踪仪D、θei、θaz解算得出，因此如何在实验中得到θu也成为解决抗干扰的关键。

2.3 坐标系夹角测试原理

坐标系夹角的测试也可简化成两个直角坐标系之间夹角的测量。测试步骤主要分为3步，如图5所示。(1)使载物台运行至二维平台的X'轴负极限处，记录此时激光跟踪仪坐标(x1，y1)始终保持y'=0，接着运行至X'轴正极限处，记录此时激光跟踪仪读数(x2，y2)。(2)使其运行至二维平台的Y'轴负极限处，记录此时激光跟踪仪坐标(x3，y3)始终保持x'=0，运行至Y'轴正极限处，记录此时激光跟踪仪读数(x4，y4)。(3)计算得出两坐标系夹角

图5 坐标夹角测试原理图

坐标变换角在静风情况下，可为上述两值中任意一个，但外场测量环境通常处于风扰中，所以两个值并不完全相等，存在偏差，若在坐标变换过程中存在abs(θ2－ θ1)＞θmax时(θmax约等于平台测试精度与平台行程的反正切值)，则认定这次坐标变换偏差大于系统需求，需要再进行一次坐标变换。

2.4 稳定平台运动控制原理

二维稳定平台需要快速定位响应，因此采用直线电机结合直线光栅尺的形式进行控制。直线电机结合直线光栅尺的形式在需求高速高精的自动化设备中大量采用，例如光刻机、数控机床等设备［6－8］。直线电机具有结构简单、安装方便、无接触、无磨损等优点［9］。同时，直线光栅尺测量直线轴位置期间没有任何其他机械传动件，因此，其可实现高精度测量。二维稳定平台实物图如图6所示。

图6 二维稳定平台实物图

文中采用位置闭环进行控制，由于外场测试需要进行长时间的精确测量，采样加速度计陀螺等间接测量等方案存在长时间工作漂移的问题，因此选用光学直接测量方案，直接进行位置实时闭环控制。激光跟踪仪最大测量范围可达80 m，在本案中需要的测量距离约15 m，在这个测试范围数量级上测试精度为μm量级，可满足测试要求。采样速率约10 kHz，传输时间约为1 ms，可满足闭环实时校正需求。利用激光跟踪仪的数据接口以及软件技术协议包，可实时将数据交由上位机进行处理运算。

稳定系统控制采用经典的PID运动控制算法［10］，通过激光跟踪仪测得值与直线光栅尺测得值之间的差值，计算得出二维平台需要反向运行的距离，然后驱动进行进行补偿运动，实习信号源位置稳定。

3 标校塔信号源抗风扰稳定系统测试

搭建的标校塔信号源抗风扰稳定系统如图7所示。在开始进行稳定前，需要进行初始位置的采样，采用多次测量求平均值的方法连续测量数十s，控制程序求得平均值后即可启动稳定平台进行系统的稳定。

图7 系统外场实物图

为了测试系统响应速度，人为对标校塔根部进行蹬踹动态干扰，数据记录如图所示。由于风载荷属于低频干扰，而且测试环境要求在4级风况下，所以人为干扰标校塔的动作在频率上是高于风载荷频率的，同时从根部造成的顶端误差可以认为属于大的误差干扰。从图8可发现，系统在约0.2 s内就回归稳态，同时系统的单轴误差均＜0.5 mm。

图8 系统稳定响应曲线图

最后对系统进行了数小时的连续测试，整个测试过程中均可快速稳定在误差范围内，稳定效果达到了设计要求。

4 结束语

本文采用激光跟踪仪实时准确地获取到了信号源的空间位置坐标，通过实时校姿程序计算得到了实时位置与初始位置之间的差值，二维稳定平台驱动控制器响应了该计算差值，驱动直线电机进行了二维方向上的位置校正，实现了信号源在二维方向上的位置稳定，实现了信号源与测试雷达之间位置的相对稳定。整套系统装置能可靠的实现信号源位置在二维方向上的位置稳定，同时装置小巧便捷，电缆走线简洁，便于外场运输装配。

［1］ 黄培康，殷红成，许小剑．雷达目标特性［M］．北京:电子工业出版社，2004．

［2］ 杨沛，邹永杰，康鹏．外场RCS测量常用标校方法分析比较［J］．电子科技，2011，24(3):69 －72．

［3］ 孙造宇，董臻，周智敏．RCS测量雷达标定过程中的误差分析［J］．现代雷达，2003(12):55－59．

［4］ 丁鹭飞，耿富录．雷达原理［M］．西安:西安电子科技大学出版社，2000．

［5］ 郑秋贞，杨华军，李东，等．机载三维成像激光雷达实时探测精度分析［J］．激光与红外，2011，41(6):612 －615．

［6］ 耿艳彪，姜万生，亢海龙，等．永磁直线同步电机驱动的开放式数控工作台设计［J］．机械设计与制造，2010(9):136－138．

［7］ 殷庆纵，刘杰．双光栅尺在高速高精度位移测量中的应用［J］．机床与液压，2012，40(7):107 －111．

［8］ 叶怀储，李志强，王鹏翔，等．基于LabVIEW的数控机床形位误差精密测量系统［J］．机电工程，2010，27(11):26－28．

［9］ 章达众，廖有用，李国平．直线电机的发展及其磁阻力优化综述［J］．机电工程，2013，30(9):1051 －1054．

［10］刘金琨．先进PID控制及其Matlab仿真［M］．北京:电子工业出版社，2003．