可逆逻辑表达式的识别和图示方法

张 乐，赵曙光，肖华军

(东华大学信息科学与技术学院，上海 201620)

可逆计算［1］是一种计算过程可逆的计算模型。在这种计算模型中，使用的能量较低，熵的增加会最小化。可逆逻辑电路设计即可逆逻辑综合是可逆计算的重要研究内容［2－5］。可逆逻辑综合，就是用给定的可逆逻辑门，按照预期的逻辑功能和可逆网络无扇出、无反馈等约束条件和限制，实现相应的可逆逻辑网络，并使得代价尽可能小［6］，其关键是以可逆逻辑门为基本单元，快速有效地生成性能指标，尽可地能优化的可逆逻辑电路。目前可逆逻辑电路的研究仍然处于理论阶段，且面临着设计规模、设计代价、电路优化等许多尚待解决的问题。

常用的可逆逻辑门都是基于异或的操作来实现的，使用该操作的逻辑门可通过简单的表达式进行描述，所以可利用异或逻辑的基本方法对可逆逻辑电路进行综合和化简，通过综合得到的异或表达式(组)来构建可逆逻辑电路。本文针对可逆逻辑电路的特点，介绍了用扩展的可逆逻辑门构造可逆逻辑电路的方法和步骤。重点阐述了可逆逻辑函数异或表达式得到可逆逻辑电路原理图的具体编程方法，并通过C语言编程实现对可逆逻辑电路的图形化显示，然后通过具体的实验证明了显示结果的有效性。

1 可逆逻辑门概述

可逆逻辑门是可逆逻辑电路的基本构件，其特点是输入端与输出端的个数相等，且各输入组合之间是一一对应关系。一个n输入n输出的二值逻辑门称为n位可逆逻辑门，或称为(n，n)可逆门。

1.1 常用的可逆逻辑门

目前，常用的可逆逻辑门主要有一位，两位以及3位可逆逻辑门。一位可逆逻辑门也称为(1，1)可逆逻辑门，如NOT门，其作用是使0变成1或1变成0。两位可逆逻辑门常用的有Feynman门，也称控制非门(Control－not Gate)，简称 CNOT 门［7］。Feynman门有两位输入，一位作为控制位(Control Bit，记为C)，另一位作为目标位(Target Bit，记为T)。3位可逆逻辑门主要有CCNOT门，由麻省理工学院的Toffoli于1980年提出，所以也称 Toffoli门［8］。

图1 NOT门

图2 CNOT门

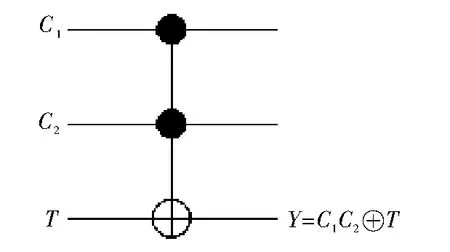
图3 Toffili门

其中，“●”表示正向控制端;“⊕”表示受控端。

1.2 扩展的可逆逻辑门

PNC(Positive/Negative Control)门［9］是 在 一 般Toffoli门的基础上进行衍变和推广而得到的，也是一个双控门，但其是正、反控制称为正/反控制门。有3个输入位，其中两个作为控制位，另一位作为目标位。控制位有正反之分，当正控制位的值为1，反控制位为0时，目标位的值取反，否则目标位的值保持不变。在可逆逻辑网络中，PNC门一般如图4所示。

图4 PNC门

其中，“●”表示正向控制端;“○”表示反向控制端;“⊕”表示受控端。

MCMT 门(Multiple Control Multiple Target Gate，多控制多目标门)［9］，又称扩展的PNC门，可记为MCMT(C;T)，其中C为控制位集合，T为目标位集合。一个具有n位控制位、k位目标位的MCMT门实现变换，其逻辑函数可表示为

MCMT门在实际应用中更为广泛，其灵活性在于，设置了不同的参数后，MCMT门可表示其他的基本可逆逻辑门:

(1)当 C=φ，T={xi0}，a0=1时，MCMT门为NOT门。

(2)当C={x0}，T={xi0}，a0=1，且x0时，MCMT门为CNOT门。

(3)当C={x0，x1}，T={xi0}，a0=1，且=x0和=x1时，MCMT门为Toffoli门。

2 可逆逻辑电路构造方法

可逆逻辑电路的可逆性特点决定了传统的逻辑门已不再使用，以异或运算为基础的可逆逻辑门将其取代，逻辑函数中“积之异或和”(ESOP)表达式取代“积之和”(SOP)表达式成为了可逆逻辑最适用的表达形式，所以由ESOP表达式(组)利用可逆逻辑门级联便可构造可逆逻辑电路。

利用MCMT门，便可实现对多输入多输出可逆逻辑电路的构造［6］。用MCMT门实现任意多输入多输出异或表达式的具体步骤如下:

步骤1 根据输入变量设置控制位集合。

步骤2 根据输出变量的个数添加辅助位作为目标位，并初始化到0状态。

步骤3 依次为每个积项添加一个MCMT门，这个MCMT门的控制端作用于该积项中的各个输入变量。

步骤4 每个MCMT门的控制位作用于相应的各个目标位，然后将各个目标位作为最后的输出。

利用MCMT门构造可逆逻辑网络具体的步骤如下:

例1 ESOP表达式形式的多输入多输出逻辑函数表达式组为

步骤1 为使网络可逆，添加4位辅助位存储输出，共8位。

步骤2 添加5个分别以第一个函数中各个积项中的变量为控制位的MCMT门，即第一个MCMT门以x0，x1，x2和x3为控制位，第二个以x0，x1和x3为控制位，第3个以x0，x1和x3位控制位，第4个以 x1和 x2为控制位，第 5 个以 x0，x1，x2，x3为控制位。

步骤3 按照步骤2，依次为逻辑函数F2，F3和F4添加与各函数中乘积项对应的MCMT门。

步骤4 将各个辅助位作为最后的输出，完成可逆逻辑电路的构造。

通过手工绘制例1的可逆逻辑电路构造结果如图5所示，其中“●”表示控制端，表示当该控制位的值为真时才对目标位起作用，“○”表示控制端，表示当该控制位的值为假时才对目标位起作用，“⊕”表示受控端。

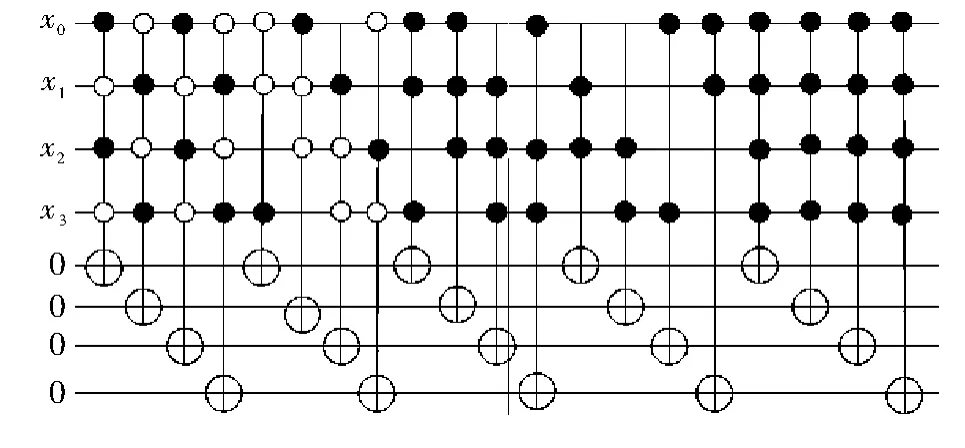
图5 利用MCMT门实现可逆逻辑电路示例

对于多输入单输出可逆逻辑电路的构造，须要利用MCMT门的一种特殊情况MCT门，简称多控门，该门只有一个目标位。通过添加一辅助位便可用MCT门实现可逆逻辑网络。CNOT门、Toffoli门以及扩展的PNC门等都属于MCT门。

用MCT门实现任意的异或表达式的具体步骤如下:

步骤1 根据输入变量设置控制位集合。

步骤2 添加一位辅助位作为目标位，并初始化到0状态。

步骤3 依次根据每个乘积项添加一个MCT门，该MCT门的控制端为相应乘积项所含输入变量的组合。

步骤4 在所有MCT门的作用下，将辅助位的输出作为最后的输出。

例2 逻辑函数的ESOP表达式为f(x0，x1，x2)=，用MCT门构建可逆逻辑电路如图6所示。

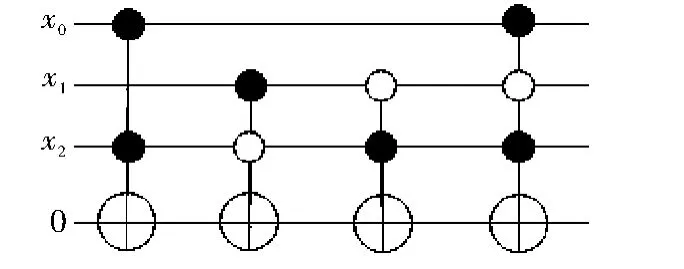
图6 利用MCT门实现可逆逻辑电路示例

3 表达式的识别和图示方法

通过对可逆逻辑电路的图形化显示的研究，能直观地反映输入输出关系，以验证是否达到预期目标。所以本文在给定可逆逻辑组合电路表达式的情况下，利用可逆逻辑电路的构造方法，通过C语言编程，以形象的方式表达可逆逻辑组合电路的输入输出关系，分析可逆逻辑电路的功能和需求，对可逆逻辑电路原理图进行图形化显示和验证。

利用C语言编程，对可逆逻辑电路进行图形化显示的具体方法和步骤如下:

步骤1 根据可逆逻辑电路的构造方法，首先需要输入逻辑函数的变量个数及输出个数，从而确定需画出的控制位个数以及需要添加的辅助位个数，以及确定是利用MCT还是MCMT门进行构造可逆逻辑电路。

步骤2 将逻辑函数以字符形式输入。由于可逆逻辑电路的逻辑表达式一般为积之异或和的形式，所以逻辑函数主要为基于异或门的组合逻辑电路，如果是其他形式的逻辑表达式，如SOP表达式，则无法得到原理图。所以，需对输入的表达式进行判断，若不是ESOP表达，则提示输入错误，需重新输入。逻辑函数的变量若输入为真，则用A～Z表示，为假则用A'～Z'表示。

步骤3 根据输入输出的个数，在相应的位置上画出与输入数相等的控制线以及与输出个数相等的目标线。

步骤4 对读取的逻辑表达式进行解析，判断表达式等号前的字符个数个，并将表达式等号后的字符型转换为整型。

步骤5 通过统计每个表达式中异或符号的个数，获得每个表达式中乘积项的个数，并保存。根据每个表达式乘积项的个数在该表达式对应的辅助线上画上“异或圆”，形如，表示目标位。

步骤6 根据获取每个表达式的乘积项的个数依次为每个函数添加对应的MCMT(MCT)门个数。具体方法是:首先取第一个函数，函数中的每个变量都已转换成了整型，通过将该变量减去字符‘A’所代表的整数值得到需要再哪条控制线上画控制点，然后判断该变量后是否有‘’’字符，如果有则画空心圆，否则画实心圆，表示该变量是取真还是取假有效。按此方法对每个函数进行处理。

步骤7 判断所有的逻辑函数是否都已处理完毕，如果处理完毕则输出最终电路图。

4 编程实现与结果分析

在Windows7系统下，用VC++6.0对上述识别和图示方法进行了编程实现。编程中特意引入EasyX库，以便在VC++6.0中实现Turbo C的绘图功能。

所编制的程序可读对应格式的文件作为输入，也可通过人机对话输入逻辑表达式。利用“*”代替键盘上无法直接输入的异或“⊕”符号。在人机对话输入提示中以及文本中，i表示输入变量的个数;o表示输出变量的个数。为了验证仿真方法的有效性，特针对多输入多输出以及多输入单输出函数分别进行如下实验:

实验1 通过读取例1中四输入四输出逻辑函数表达式组的txt格式文件如图7所示，运行结果如图8所示。

图7 四输入四输出异或逻辑表达式组的输入

图8 四输入四输出逻辑表达式组的可逆逻辑图显示结果

该例实际上涉及了非可逆逻辑表达式到可逆逻辑表达式的转换。受到可逆性制约，可逆逻辑网络的输出数必须等于输入数，所以需添加辅助位来保存逻辑函数的输出值，在此添加4位辅助位存储输出，并初始化到0状态，依次为每个积项(AND项)添加一个MCMT门，这个MCMT门的控制端作用于该积项中的各个变量，每个MCMT门的控制位作用于目标位，作为最后的输出。通过与例1手工绘制的可逆逻辑原理图比较，可得该显示结果准确有效。

实验2 针对3输入单输出异或逻辑表达式即例2的逻辑表达式 F(A，B，C)=AC⊕BC'⊕B'C⊕AB'C进行实验，其输入过程和运行结果分别如图9，图10所示。

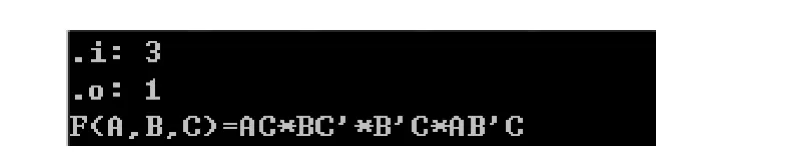
图9 三输入单输出异或逻辑表达式的输入

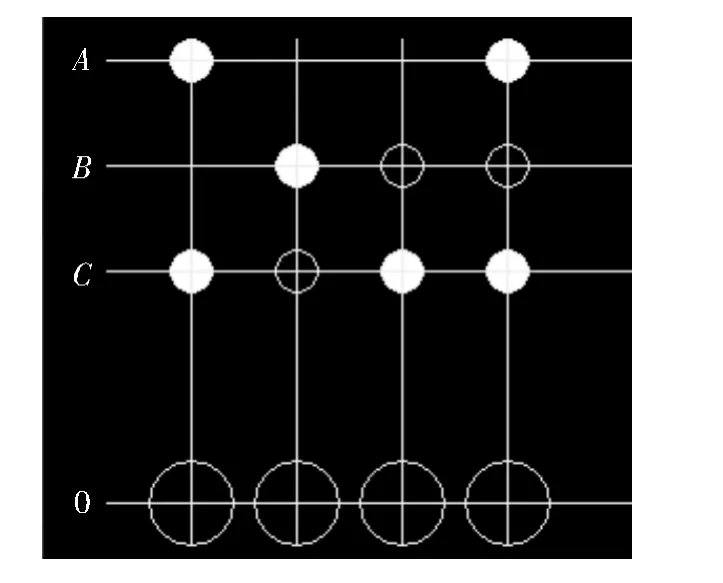
图10 三输入单输逻辑表达式的可逆逻辑图显示结果

该例涉及了非可逆逻辑表达式到可逆逻辑表达式的转换。可逆逻辑电路的输出数必须等于输入数，所以需添加辅助位来保存逻辑函数的输出值，在此添加1位辅助位存储输出，并初始化到0状态。图中A，B，C的3个控制端，白色实心圆表示该控制位取真有效，空心小圆表示该控制位取反有效，辅助位上大圆表示控制位对目标位的控制。通过与例2手工绘制的可逆逻辑原理图进行比较，可知该显示结果准确有效。

5 结束语

介绍了常用可逆逻辑门，针对可逆逻辑电路的特点，介绍了用扩展的可逆逻辑门构造，可逆逻辑电路的方法和步骤。重点阐述了通过编程识别可逆逻辑函数异或表达式，提取可逆逻辑电路结构信息的具体算法。通过C语言编程实现了对可逆逻辑电路原理图的图形化显示，并通过实验1和实验2验证了显示结果的有效性。

［1］ Frank M P．Introduction to reversible computing:motivation，progress，and challenges［C］．Proceedings of the 2nd Conference on Computing Frontiers，2005:385 －390．

［2］ Landauer R．Irreversibility and heat generation of the computing process［J］．IBM Journal of Research and Development，1961，5(3):183 －191．

［3］ Bennett C H．Logical reversibility of computation［J］．IBM Journal of Research and Development，1973，17(6):525－532．

［4］ Andrel B Khlopotine，Perkowski M，Pawel Kerntopf．Reversible logic synthesis by iterative composition［C］．Proceedings of IWLS，2002:261 －266．

［5］ Miller D M，Maslov D，Dueck G W．A transformation based algorithm for reversible logic synthesis［C］．Anaheim California，USA:Design Automation Conference(DAC)，IEEE/ACM，2003:318 －323．

［6］ Fredkin E，Toffoli T．Conservative logic［J］．International Journal of Theoretical Physics，1982(21):219 －253．

［7］ Feynman R．Quantum mechanical computers［J］．Optic News，1985(6):11－20．

［8］ Toffoli T，De Bakker J W，Van Leeuwen Jeds．Reversible Computing Automata，Languages and Programming［M］．New York:Springer Conpration，1980．

［9］ 管致锦．可逆逻辑综合［M］．北京:科学出版社，2010．