＊具有耗散和阻尼项的Kirchhoff型方程吸引子的存在性

王海英，李桂莲（太原理工大学数学学院，太原030024）



＊具有耗散和阻尼项的Kirchhoff型方程吸引子的存在性

王海英，李桂莲
（太原理工大学数学学院，太原030024）

摘 要：对具有耗散和阻尼项的Kirchhoff型方程，在满足一定的初边值的条件下，首先运用Gronwall引理，并结合Sobolev嵌入定理，证明出该方程有界吸收集的存在性；其次通过验证半群满足紧性，证明出该方程吸引子在广义空间中的存在性。

关键词：Kirchhoff型方程；Gronwall引理；条件（C）；吸引子

Masamro［1］提出具有耗散和阻尼项的Kirchhoff型方程，并运用Faedo－Galerkin方法证明了该方程在满足边界条件（2）和初始条件（3）情况下整体解的存在性，但是对于该方程吸引子的存在性一直没被研究。本文中将利用文献［3］中提出的一种新的验证半群紧性的方法———条件（C）来研究该方程吸引子的存在性。

假设Ω是R2中具有光滑边界Ω的有界开区域，本文研究下面Kirchhoff型方程

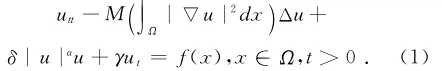
在边界条件为

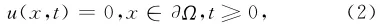
初始条件为

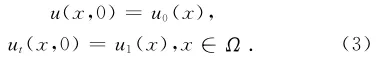
的吸引子的存在性。

式中：δ，α，γ均为正常数；f（x）∈L2（Ω）；u0（x），u1（x）∈L2（Ω），均为给定的初值函数。非线性函数M（s）满足下面的条件

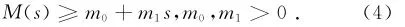
令，H＝L2（Ω），V＝H10（Ω），H和V的内积和范数分别用（·，·），｜·｜和（（·，·）），‖·‖表示，它们的内积分别定义为为方便描述，记空间E0＝V×H．

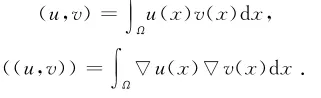
（A－12）＝V＊．

根据Poincaré不等式，有）

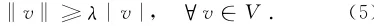
式中，λ是A

1

2在空间H10（Ω）中的第一特征值。

1　预备知识

为了证明问题（1）－（3）式吸引子的存在性，需要下面的抽象理论。

定义1［3］Banach空间X中的C0半群｛S （t）｝t≥0满足条件（C），如果对ε＞0和X中的任意有界集B，存在t（B）＞0和X的有限维子空间X1，

通讯联系人：李桂莲，女，教授，（E－mail）liguilian＠tyut．edu，cn使得｛‖PS（t）x‖X∶x∈B，t≥t（B）｝有界，并且当t≥t（B），x∈B时有‖（I－P）S（t）x‖X＜ε．这里P∶X→X1是有界投影。

引理1［3］设｛S（t）｝t≥0是Hilbert空间M上的C0半群，那么｛S（t）｝t≥0存在吸引子Λ，当且仅当

1）｛S（t）｝t≥0满足条件（C）；

2）｛S（t）｝t≥0在M中存在有界吸收集。

引理2［1］假设δ，α，γ＞0，非线性函数M（s）满足条件（4），则对任意给定的f∈H，u0，u1∈H，初值问题（1）～（3）在区间［0，T］上存在唯一解u，满足u ∈C［0，T］，）（V，ut∈C［0，T］，）（H．

问题（1）－（3）式解的存在性的证明可参考文献［1］，利用Faedo－Galerkin方法并结合本文第2部分即可得到，故省略不证。

2　E0中的有界吸收集

定理1 假设条件（4）成立，则问题（1）－（3）式在空间E0中存在有界吸收集。其中，以0为中心μ为半径的球B0＝B0（0，μ）是问题（1）－（3）式的有界吸收集。

证明 用v＝ut＋εu在H中和方程（1）作内积，可得

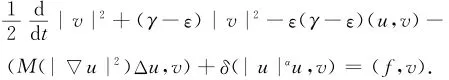
式中：δ（｜uα｜u，v）＝

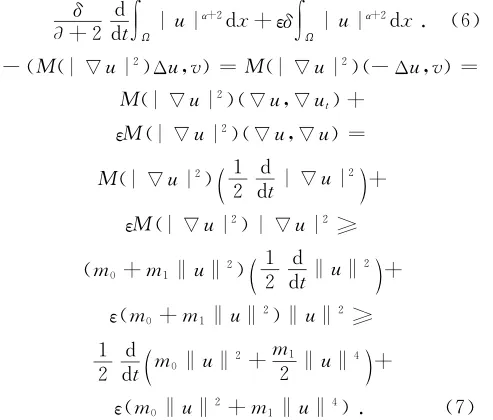
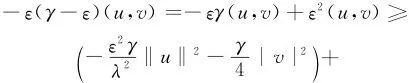
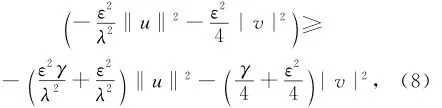
而且

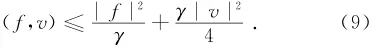
由式（6）、式（7）、式（8）、式（9）可得

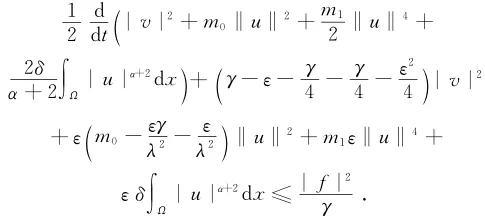
取充分小的ε＞0，使得

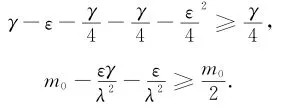
则有d

d

t｜v｜2＋m0‖u‖2＋m1

2‖u‖4

（

＋

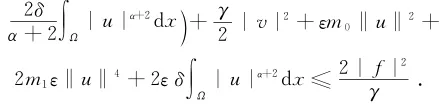
取ε0＝minγ

2，

｛｝

ε，又因α＞0，即得d

d

t｜v｜2＋m0‖u‖2＋m1

2‖u‖4

（

＋

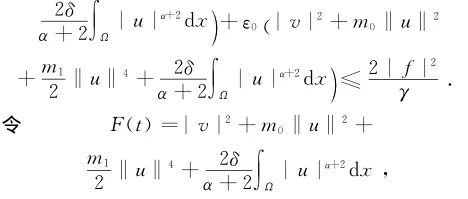
从而dF（t）＋εF（t）≤C， C＝2｜f｜2

．

dt0γ

根据Sobolev嵌入定理，当‖u（0）‖2有界时，F（0）有界，由式（10）得limF（t）≤ρ2，式中，ρ2＝εC．固定

t→∞0

μ＞ρ，并假设F（0）≤R，则当t≥t0＝t0（R，ρ）＝

ε10

lgμ2R

－ρ2时，有｜v｜2＋m0‖u‖2≤F（t）≤μ2．

这样，得到了E0中的以0为中心μ为半径的球B0＝B0（0，μ）是问题（1）～（3）中的有界吸收集，即对E0中的任意有界集B，存在t0（B），使得当t≥t0（B）时，有｛S（t）｝BB0．

3　吸引子的存在性

定理2 假设条件（4）成立，则问题（1）～（3）存在吸引子Λ，以E0的范数吸引E0中的任意有界集。

证明 由引理1及定理1只要证明半群｛S （t）｝t≥0满足条件（C）即可．设λ1，λ2，…，为A的特征值，ω1，ω2，…，为其对应的特征向量，当j→∞时，λ1＜λ2≤λ3≤，…，λj→∞，并且｛ωk｝∞k＝1构成V的直交基，记Vm＝span｛ω1，ω2，…，ωm｝．对ε＞0，存在m使得

｜（I－Pm）f｜≤ε．（11）

式中，Pm：V→Vm是直交投影。

u1＋

u2．用v2＝u2t＋σu2在H中和方程（1）作内积可得类似式（6）估计有

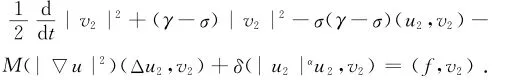
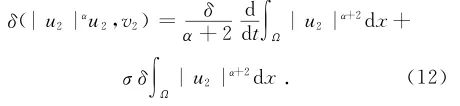
结合式（4）、式（10）

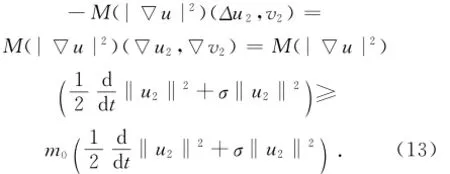
类似式（8）

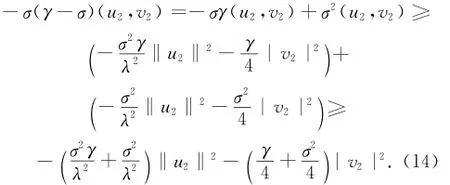
和

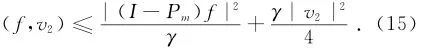
结合式（12）、式（13）、式（14）、式（15）可得

取充分小的σ＞0，使得

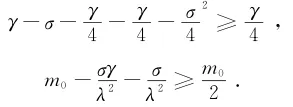
则有d d t｜v2｜2＋m0‖u2‖2

［

＋

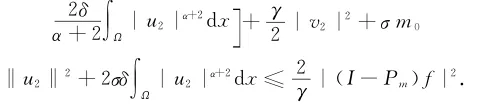
取σ0＝minγ

2，

｛｝

σ，又因α＞0，结合式（11），即得

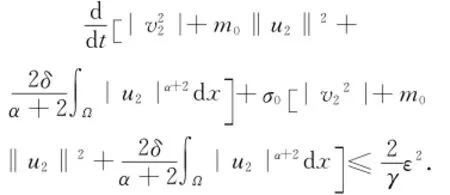
记E（t）＝｜v2｜2＋m0‖u2‖2＋

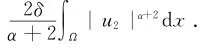
从而

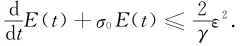
利用Gronwall引理得到

取t2充分大满足t2－t1≥1

σ

0 lnμ2

ε2，则当t≥t2时，

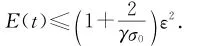
即半群｛S（t）｝t≥0在E0中满足条件（C），定理2得证。

参考文献：

［1］ Masamro H，Yoshio Y．On some nonlinear wave equations 2：global existence and energy decay of solutions［J］．Fac Sci Univ Tokyo Sect，1991，38：239－250．

［2］ 李庆霞，谭忠．具有耗散和阻尼项的kirchhoff型方程的整体解存在性［J］．厦门大学学报：自然科学版，2002，41（4）：419－422．

［3］ Ma Q F，Wang S H，Zhong C K．Necessary and sufficient conditions for the existence of global attractors for semigroup and applications［J］．Indiana University Math，2002，51（6）：1541－1559．

［4］ MA Qiaozhen，ZHONG Chengkui．Existence of strong global attractors for the hyperbolic equation with linear memory［J］．Applied Mathematics and Computation，2004，157（3）：745－758．

［5］ 马巧珍，孙春友，钟成奎．非线性梁方程强一致吸引子的存在性［J］．数学物理学报：A辑，2007，27（5）：941－948．

［6］ 陈小豹，马巧珍．非线性可拉伸梁方程强一致吸引子的存在性［J］．西北师范大学学报：自然科学版，2008，44（6）：1－6．

［7］ 李志宇，马巧珍．非线性可拉伸梁方程的一致吸引子［J］．西南师范大学学报：自然科学版，2012，37（4）：34－37．

（编辑：刘笑达）

Existence of Attractors for a Kirchhoff Type Equation with Damping and Restoring Terms

WANG Haiying，LI Guilian
（College of Mathematics，Taiyuan University of Technology，Taiyuan030024，China）

Abstract：Kirchhoff type equation with damping and restoring terms was studied when it satisfies certain boundary and initial conditions．Firstly，Gronwall lemma and Sobolev Embedding Theorem，were combined to establish the existence of a bounded absorbing set．Secondly，the existence of attractors in general space was proved by verifying that semi－group satisfies compaction．

Key words：Kirchhoff type equation；Gronwall lemma；condition（C）；attractor

作者简介：王海英（1988－），女，河北邯郸人，硕士生，主要从事偏微分方程研究，（E－mail）why415＠163．com，（Tel）18334705139

基金项目：国家自然科学基金资助项目：非线性肿瘤免疫系统的随机动力学研究（11172194）

收稿日期：＊2014－10－27

DOI：10．16355／j．cnki．issn1007－9432tyut．2015．03．022

文献标识码：A

中图分类号：O175．2

文章编号：1007－9432（2015）03－0357－04