三维空间域多径信道模型的AOA和TOA特性分析*

史书明，姚颖莉，周　杰

（1.常州工学院，计算机信息工程学院，江苏 常州 213003；2.南京信息工程大学，气象探测与信息处理重点实验室，江苏 南京 210044）

三维空间域多径信道模型的AOA和TOA特性分析*

史书明1，姚颖莉2，周杰2

（1.常州工学院，计算机信息工程学院，江苏 常州 213003；2.南京信息工程大学，气象探测与信息处理重点实验室，江苏 南京 210044）

在三维空间域提出了一个几何模型，其散射椭圆半球体的中心在移动台（MS），基站（BS）被置于散射球体外部。该模型可以在方位角和仰角平面同时描述多径波的到达角度和到达时延，据此推导出电磁信号分别在MS和BS端关于到达角度的联合、边缘概率密度函数封闭式表达式。除此之外还推导出到达时延的联合概率密度函数的封闭式表达式。该三维模型适用于低MS天线和高BS天线且重要散射体分布在移动台附近的室外宏蜂窝通信环境。此外还对数值仿真实验获得的理论数据进行分析比较，进一步验证信道参数估计结果符合理论和经验。

到达角度；几何散射模型；概率密度；到达时延；多径波

0　引言

近年来，为满足人们对无线通信不断增长的容量需求，通信系统的空时参量越来越受到人们广泛关注。空间信道模型描述了多径分量的到达角度和到达时延的相关数据信息，在设置天线阵列的无线通信系统的性能评估方面作用显著。所有现存的几何模型基本上都是二维的，如离散均匀模型[1-2]、椭圆散射模型[3]、圆形散射模型（CSM）[4]、高斯散射密度模型[5]、高斯 AOA 模型[6]等，上述模型均认为信号传输发生在连接发射和接收天线顶端的一个平面上，仅推导和计算在水平面内的空时信道参数。一些学者相继提出了许多关于无线电信道的时间和空间特性的几何模型，但大多在空间角度的研究上存在明显的不足。针对宏小区环境下的移动无线通信问题，本文提出了一个三维空间域多径信道几何模型。重点研究模型的空时参量，给出电磁信号分别在移动台和基站的联合、边缘概率密度函数封闭式表达式以及传输路径时延的封闭式表达式。此外还同时在方位角和仰角平面描述多径波的到达角度和到达时延，允许在上述两平面内独立控制其角度扩展，并在此基础上分析影响其时延特性的部分因素。

1　系统模型相关理论

本文提出的三维模型其主要散射体均匀地分布在MS附近，如图1所示。图中，a＜D，b≤a，从BS到MS的直达路径长度可表示为 dLOS。本文中的椭球体可被下式定义：

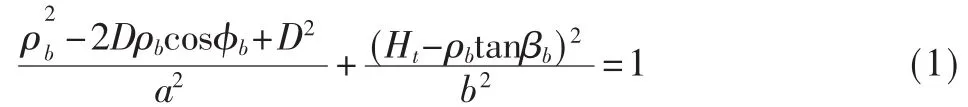
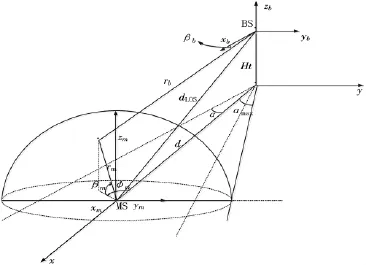
图1　球体内MS为中心的散射体均匀分布模型

2　系统的三维空间特性AOA

2.1电磁信号在MS端的到达角度

方位角的边缘概率密度函数可通过对其联合概率密度函数的变量依次积分获得。同理可得仰角的边缘概率密度函数。利用雅可比变换可得MS处联合概率密度，对其rm进行积分，可得：

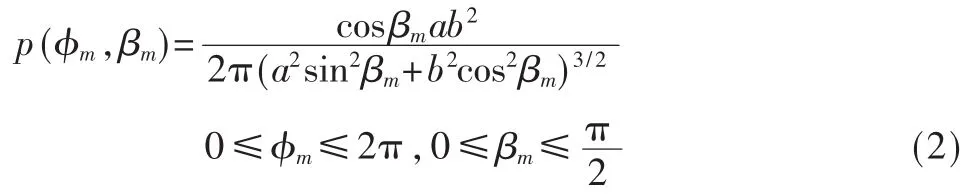
对上式的 βm进行积分并通过 t＝sinβm变量代换得方位角在（0，2π）内均匀分布，且与 BS天线的高度无关。对式(2)中的φm进行积分即可获得关于仰角的概率密度函数：

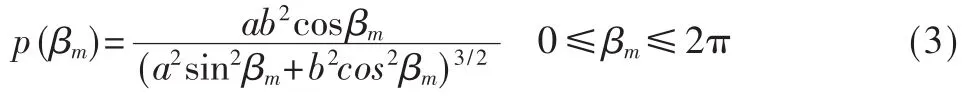
从上式可以看出，仰角βm的概率密度函数的图形形状仅与椭球体b/a的比率有关。从式(2)和式(3)可见，MS的仰角与方位角是统计独立的。

2.2电磁信号在BS端的到达角度

利用雅可比转换式，可得BS处的联合概率密度函数。对其rb的所有可能取值进行积分，可得其关于角度的边缘概率密度函数：

其中，rb1和 rb2是从 BS端角度为(φb，βb)处引的一条直线与半椭球体的交点。

图2示出了半椭球体与φb确定的平面的交点构成的半椭圆Sφ的几何形状。椭圆的中心、径向长度均如图所注。sinφmax＝a/D，与 BS的天线高度无关。综上，概率密度函数 p(φb)表达式为：

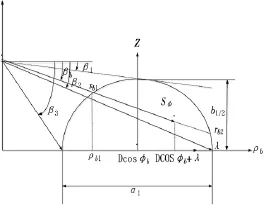
图2　参数Sφ计算模型图

从上式可见BS处方位角概率密度函数与轴长b无关。

3　系统的时延特性TOA

τ为传输时延，计算可得rm为：

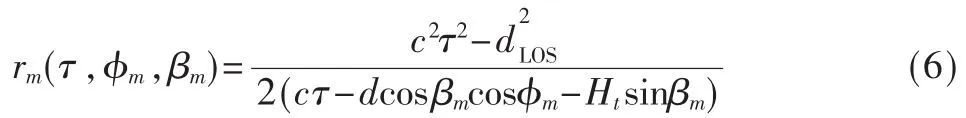
TOA/AOA的联合概率密度函数表达式为：

其中 rm在式(6)中已给出，利用雅可比变换并带入式(7)中即可得到TOA/AOA的联合概率密度函数，其公式如下：

相似地，在BS的对应角的联合概率密度函数也可得到，其中V＝2πa2b/3。利用积分依次可得BS端到达时延的相应联合概率密度函数式如下：

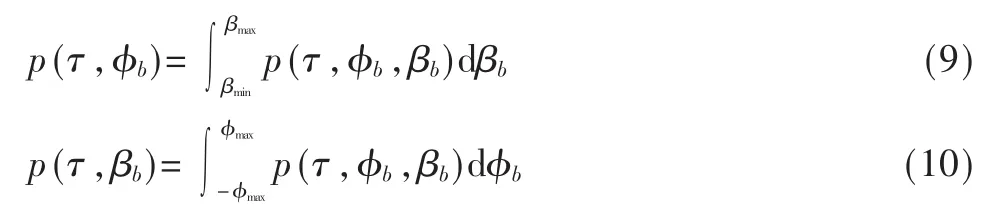
同理可得MS端的方位角、仰角到达时延联合概率密度函数。对上述两式中任一公式的相应角进行积分即可获得到达时延边缘概率密度函数，即：

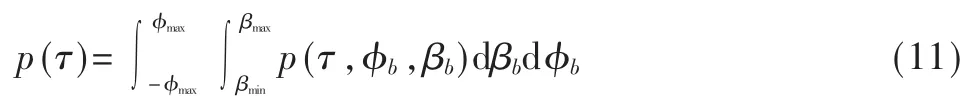
4　数值结果与分析

仿真实验的结果将在此部分进行分析。图3描述的为不同b/a取值情况下仰角βm对应的概率密度函数的三维图，从图中可以发现，当b/a较大时，在竖直平面上的切平面较大，从而多径信号AOA的概率密度相对较大。从图中还可发现移动台BS端的发射信号基本在小角度（βm为零度）或者 b/a参数值较大处，而在大角度（βm为直角）时其概率密度较小，几乎为零。所有曲线中最常发生的角在βm=0处，此时3D模型转化为2D模型，无论 b/a数值如何变化，其切平面都相同，故俯仰平面AOA概率密度值相等为零。研究比较发现：本文提出的模型，其基站处方位角的概率密度函数(见式(5))不同于散射半径为a的二维CSM模型的PCSM(φb)。

图4描述的是本文提出的半椭球模型和CSM模型在方位角平面对应不同D值的概率密度样值函数分布情况。正是由于深度和高度的综合作用，与CSM相比，本文提出的椭球模型的离轴散射体才会与其不同。

图3　MS终端的联合概率密度分布

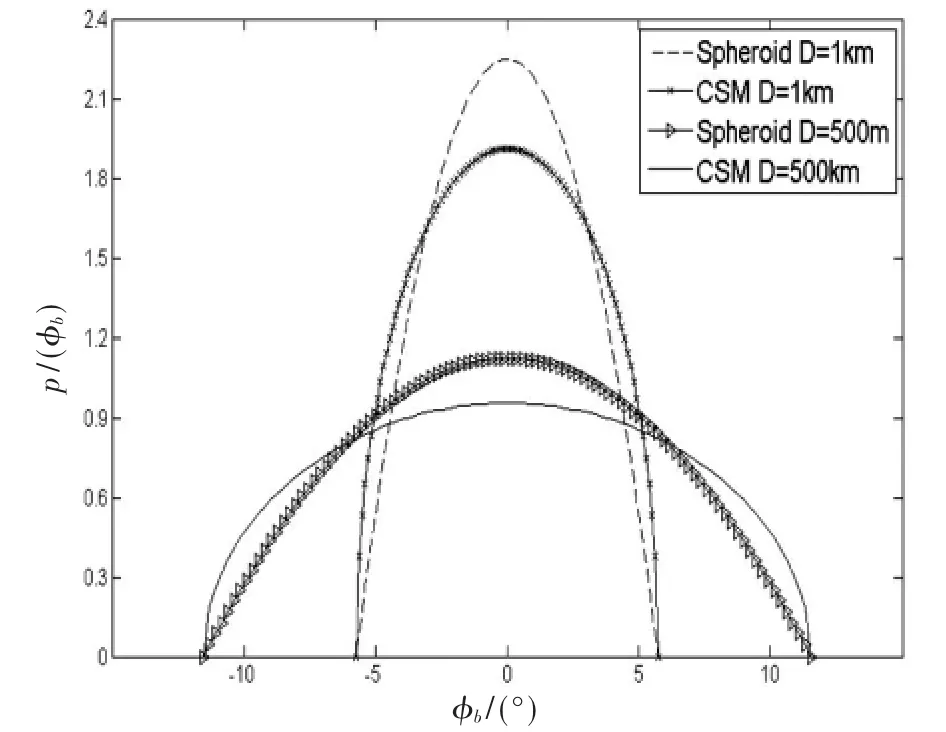
图4　BS基站方位角概率密度分布

图5、图6分别描述了关于方位角以及仰角的TOA联合概率密度函数的几何分布情况。从图5可以发现，由于空间分布关于竖直平面对称（见图1），使得TOA联合概率分布波形被挖掉时延不存在的两片区域，左右处于对称状态，故其图形结果在-Φm～Φm之间对称分布。移动台接收信号基本在小角度（Φm=0）处，而在角度增大至180°时其概率密度分布相当小，且其关于方位角的TOA概率函数值在Φm=0处到达峰值。由图6的波形分布可知，a/D不断增加，关于仰角的TOA联合概率密度函数值不断衰弱，当传输时延超过最大传输时延即超过散射区域，其概率密度为零；当俯仰平面的角度 βm不断增大时，远离MS端的散射体逐渐增多，电磁信号的反射和折射概率相对较大，故导致关于仰角的TOA概率密度不断减小[9]。如果令式（8）中的 βm和 Ht值均为零，则可由本模型推导出文献3中提出的一个二维模型。

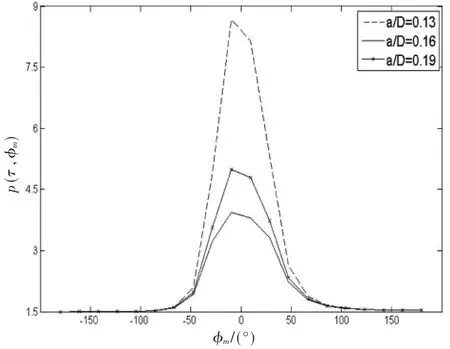
图5　方位角—时延边缘概率密度分布

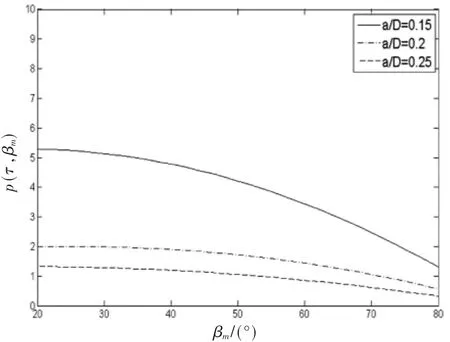
图6　仰角—时延边缘概率密度分布

5　结语

针对室外宏蜂窝环境等因素造成的多径信道衰落，本文提出的 3D模型的几何参数有：椭球体的轴长 a、b，基站天线的高度Ht，负责发送的基站与负责接收的移动台之间的水平距离D。揭示了此模型下BS和MS端在水平面和俯仰面上各信道参数的变化特征。在移动台处，方位角的多径波均匀分布，仰角的多径波分布仅与a和b有关。在基站处，方位角的概率密度函数与单一变量 a/D密切相关，而仰角的概率密度函数不仅与 a/D有关，还与b/D和Ht/D有关。对于时延特性，其概率密度函数也与a/D有密切关系。当存在的散射体与发射机和接收机部分的距离不断增加，传播时延会相应的延长。本文提出的模型在宏蜂窝环境中非常有用，基于本文对散射区域水平与垂直方向的角度扩展，使用平面天线阵列对无线电通信系统进行性能分析的精度会越来越高。而这些性能分析又能够在进一步提高通信系统流数据速率方面加以使用。

[1]LEE W C.Mobile communications engineering[M].New York：McGraw-Hill Professional，1982.

[2]SUZUKI H.A statistical model for urban radio propagation[J]. Communications，IEEE Transactions on，1977，25(7)：673-680.

[3]ERTEL R B，REED J H.Angle and time of arrival statistics for circular and elliptical scattering models[J].Selected Areas in Communications，IEEE Journal on，1999，17(11)：1829-1840.

[4]PETRUS P，REED J H，RAPPAPORT T S.Geometrically based environments[C].Global Telecommunications Conference，1996.GLOBECOM′96.′Communications：The Key to Global Prosperity.IEEE，1996(2)：1197-1201.

[5]JANASWAMY R.Angle and time of arrival statistics for the Gaussian scatter density model[J].Wireless Communications，IEEE Transactions on，2002，1(3)：488-497.

[6]NAWAZ S J，KHAN N M，PATWARY M N，et al.Effect of directional antenna on the Doppler spectrum in 3-D mobile radio propagation environment[J].Vehicular Technology，, IEEE Transactions on，2011，60(7)：2895-2903.

[7]ZHOU J，CAO Z G，HISAKAZU K.Asymmetric geometricalbased statistical channel model and its multiple-input and multiple-output capacity[J].IET Communications，2014，8(1)：1-10.

Analysis of the AOA and TOA properties of the 3D spheroid model

Shi Shuming1，Yao Yingli2，Zhou Jie2
(1.School of Computer Information and Engineering,Changzhou Institute of Technology,Changzhou 213002，China；2.Laboratory of Meteorological Observation and Information Processing，Nanjing University of Information Science and Technology, Nanjing 210044，China)

A three-dimensional(3D)geometric model is presented with a mobile station(MS)located at the center of a 3D scattering semi-spheroid and a base station(BS)located outside of the semi-spheroid.The presented model can describe simultaneously angle of arrival and time of arrival of multipath waves in the azimuth and elevation planes.Closed-form expressions for joint and marginal probability density functions(pdfs)of the angle of arrival are provided as seen from the mobile station and base station are derived.Furthermore,closed-form expressions for joint pdfs of the time of arrival observed at the MS and the BS in correspondence with azimuth and elevation angles are derived.The model is suitable in a macro-cellular environment with a low MS and an elevated base station antenna,where significant scatterers are distributed about the former.Moreover,the obtained theoretical results with some 3D scattering models are compared further to validate the rationality of the proposed model.

angle of arrival；geometric scattering model；probability density；time of arrival；multipath wave

TN911.6

A

10.16157/j.issn.0258-7998.2015.10.027

国家自然科学基金面上项目(61372128，61021062)；江苏省高校自然科学研究重大项目(14KJA510001)；中国博士后基金(010986678)

2015-04-10)

史书明（1979-），女，讲师，主要研究方向：计算机网络。

姚颖莉（1991-），女，硕士研究生，主要研究方向：移动通信理论及信号处理方法与技术。

周杰（1964-），男，博士，教授，博士生导师，主要研究方向：移动通信理论、无线传感网和无线接入网等。

中文引用格式：史书明，姚颖莉，周杰.三维空间域多径信道模型的 AOA和 TOA特性分析[J].电子技术应用，2015，41 (10)：100-102，106.

英文引用格式：Shi Shuming，Yao Yingli，Zhou Jie.Analysis of the AOA and TOA properties of the 3D spheroid model[J]. Application of Electronic Technique，2015，41(10)：100-102，106.