电磁矢量传感器EVS对MIMO多天线系统影响研究*
李峻松,周 杰
(南京信息工程大学 电子与信息工程学院,江苏 南京 210044)
电磁矢量传感器EVS对MIMO多天线系统影响研究*
李峻松,周杰
(南京信息工程大学 电子与信息工程学院,江苏 南京 210044)
为提高多输入多输出(MIMO)无线通信系统的性能,建立了基于标量传感器的均匀矩形天线阵列(URA),并将电磁矢量传感器信号处理方式与MIMO信号处理方式有机结合,建立了基于电磁矢量传感器的天线阵列。推导了各天线阵列的空间衰落相关性公式,分析了方位角和仰角的平均到达及角度扩展等参数变化对于相关性的影响。确立了MIMO系统发射和接收两端的相关性协方差矩阵,分析了不同天线阵列的信道容量大小。通过仿真模拟,证明了电磁矢量传感器阵列具有优异的性能和良好的应用前景。
多输入多输出;天线阵列;电磁矢量传感器;空间衰落相关性;信道容量
0 引言
无线通信系统中天线阵列 (Antenna Arrays,AAs)的选择对信道容量和信号质量的提高有着重要的意义。由于天线阵列的性能主要基于多径信道空间特性的开发,因此提高角度参数对于天线阵列性能影响的认知势在必行。前人已针对到达方位角(Azimuth of Arrival,AOA)概率密度函数(Probability Density Functions,PDFs)在均匀分布或者拉普拉斯分布下的均匀天线阵列(Uniform Antenna Arrays,UAA)的空间衰落相关性(Spatial Fading Correlation,SFC)进行研究并取得珍贵的成果[1-2]。由于现今移动通信设备的随身特性,要求手持设备天线处于任意随机的空间位置上都可以获得良好的信号,因此只考虑到达方位角的二维天线阵列模型有所局限[3]。在此基础上,进一步考虑综合到达方位角和到达仰角共同影响的三维环境下角度参数对于天线阵列的空间衰落相关性的影响有着重要的意义。
在多输入多输出(Multiple Input Multiple Output,MIMO)技术中,多天线被应用于基站(Base Station,BS)和移动站(Mobile Station,MS)中是为高效利用空间信道的多径分量。信道容量随天线阵元个数的增加而线性增大,但是阵元间距的减小同时会导致增大阵元间相关性,甚至受到互耦效应的影响[4]。一种获得良好性能的方式是有效地隔离BS、MS天线单元以获得较大的分集阶数。在BS引入多天线并没有明显的技术难度,但是在MS引入多天线却难以实现。因此,本文介绍了均匀矩形阵列(Uniform Rectangular Array,URA)和电磁矢量传感器(Electromagnetic Vector Sensor,EVS)天线阵列两种小型天线阵(Compact Antenna Array CAA)模型,其中 EVS阵列是替代 URA等传统标量传感器阵列(Scalar Sensor Array,SSA)的优良选择。
如图1所示,单点EVS模型由3个正交的电偶极子和3个正交的磁偶极子供电配置而成,其偶极子和磁环尺寸均小于半个波长,同时可感应电磁信号的3个时分电场分量和相应的3个磁场分量具有同点极化分集接收能力。EVS已被广泛用于雷达、声呐等定向应用方面。由于其具有的极化多样性较传统的双极化系统能够带来更大的信道容量,因而在移动通信系统中亦有着良好的应用前景。EVS具有紧凑的结构,故可在一个天线阵列中配置多个EVS以获得更好的性能。MIMO信道容量与各天线单元间的SFC密切相关,所以研究小型天线阵中各阵元间的SFC有着重要的意义。
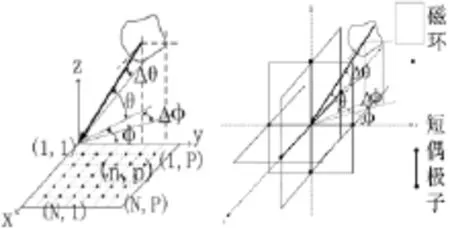
图1 URA阵列和单点EVS模型
本文的研究目的是尝试建立不同小型天线阵模型的相关性方程,确立MIMO系统发射和接收两端的相关性协方差矩阵,以改善无线信道的性能;同时深入分析平均到达方位角(Mean Azimuth of Arrival,MAOA)、方位角扩展(Azimuth Spread,AS)、平均到达仰角(Mean Elevation of Arrival,MEOA)和方位角扩展(Elevation Spread,ES)等不同的角度参数对于SFC的影响,研究系统性能对于不同参数的敏感性;最后分析采用不同天线阵列模型的MIMO多天线系统的信道容量,以直观表征不同天线阵列条件下的系统性能。
1 三维信道模型
本文针对定向频率非选择性瑞利衰落信道模型进行性能分析。利用多个不同时延的信道的线性叠加进行MIMO信道建模,其信道脉冲响应表达式可为[5]:

其中,αj(t)为零均值的复独立同分布随机变量,a(Θj)为天线阵列的导向矢量(Steering Vector,SV);JMPC为发射端天线总数;Θ=[θ,φ,γ,η]T为空间矢量参数,其中0≤φ<2π、0≤θ<π分别为方位角和仰角,0≤γ<π/2、-π≤η<π分别表示辅助极化角和极化相位差。假设URA中的天线单元为垂直极化的,则Θ只与φ和θ取值有关。因此,对于参考相位位于xoy平面原点的N×M个阵元的URA,其导向矢量方程为:

其中:aN(μ)=[1,ejμ,…,ej(N-1)μ]T,μ=kwdxcosφsinθ;aM(v)= [1,ejv,…,ej(M-1)v]T,v=kwdysinφsinθ,dx和 dy分别为平行于x轴和y轴阵元间距。vec(·)将N×M矩阵映射成NM×1的列向量。
对于EVS,其导向矢量方程为[6]:
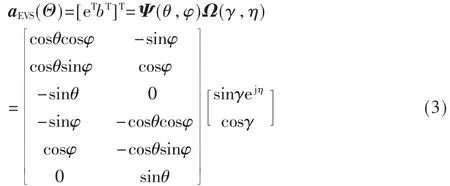
最后,对于引入EVS的阵列,其联合导向矢量为:
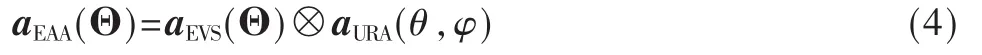
其中,⊗为 kronecker乘积,aEAA和aURA分别为实际情况下EVS和URA的导向矢量。
2 空间衰落相关性
对于URA,阵元m和阵元n之间的SFC方程定义为[6-7]:

其中 E[·]表示期望,(·)*表示复共轭,hm表示阵元 m信道脉冲响应(即接收信号能量)均值,an(θ,φ)为阵元 n的导向矢量,p(θ,φ)为多径分量 AOA联合概率密度函数。在此假设天线数量足够多,故式(5)中的连续模型可以良好地近似式(1)中的离散模型。另假设AOA与EOA相互独立,则 p(θ,φ)可分解为 p(θ)p(φ)。AOA在[φ0-Δφ,φ0+Δφ]范围内均匀分布[1],其中 Δφ和 φ0分别为 AS和 MAOA。同样,EOA在[θ0-Δθ,θ0+Δθ]范围内均匀分布,其中 Δθ和θ0分别为ES和MEOA。
在天线的每点阵元上配置EVS构成小型天线阵列,考虑包括极化域在内,则式(5)将转变为如下式[8]:
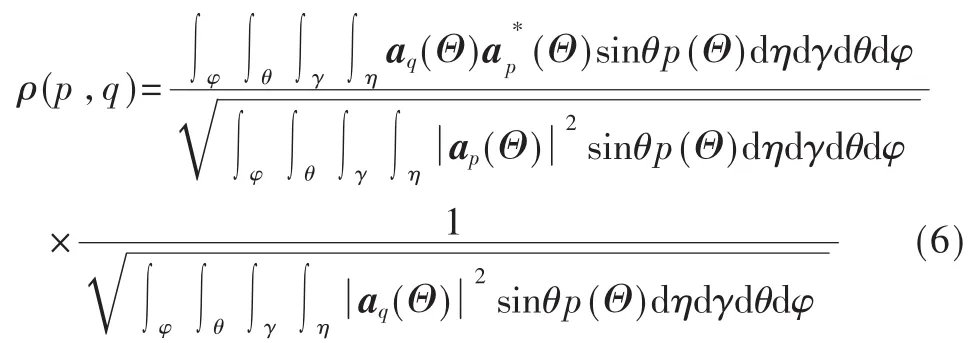
假设 p(γ)和p(η)分别为在[0,π/2]和在[-π,π]上均匀分布,故可推导出阵元m所接收入射信号的第p空间极化分量与阵元n所接收入射信号的第q空间极化分量之间的SFC的闭合表达式:

其中:
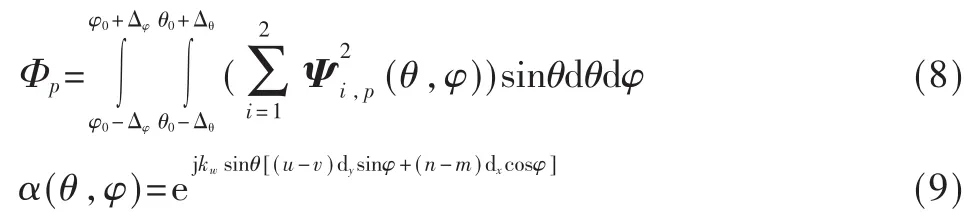
Ψi,p为矩阵Ψ第i列的第p个空间分量。
3 MIMO天线阵列信道容量
在对无线信道容量评估中,通常MIMO多径衰落信号信道容量作为衡量包含信道链接端点的信道质量的一种方式。如果在接收端已知多径信道信息,而发送端未知时,可在发送端假设信道矩阵服从零均值空间白噪声模型。为使信道遍历容量最大化,最优的策略是将功率平均分配到每个发送天线上,即遍历容量最大化的输入协方差矩阵为Rx=(ρ/MBS)IMBS。因此,遍历容量可表示为:
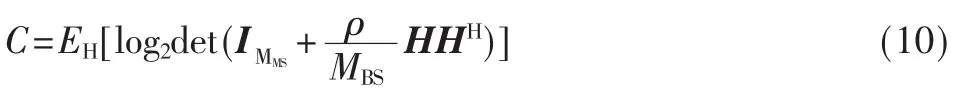
其中,MBS和 MMS分别为 BS和 MS的天线阵元数量;IMMS为 MMS阶单位矩阵;ρ为传输信号的信噪比(SNR);为 MIMO多天线信道矩阵[9],RMS是 MS多天线阵元间衰落信号相关矩阵,RBS是BS多天线阵元间衰落信号相关矩阵,Hw是具有相同分布的复高斯随机矩阵,表示矩阵的转置。由于在系统级的天线设计中基站的天线阵列形式一般不能任意选择,考虑理想的垂直极化非相关天线阵列,将基站相关矩阵RBS表示为RBS= I。(·)H表示共轭转置,EH(·)为求数学期望以对信道矩阵H的分布进行均值分析。
4 仿真结果与分析
此节将对天线阵列的空间衰落相关性和所构成MIMO系统的信道容量进行仿真模拟,验证所得结果与理论推导的结论是否符合,直观显示不同的天线阵列模型对于系统性能的影响。此处仿真均假设AOA和EOA的概率密度函数均符合均匀分布,MS多天线阵列包含6×6个阵元。
4.1空间衰落相关性
图2给出天线阵列在MAOA和MEOA等于90°、AS和ES等于30°时空间衰落相关性与天线距离间的关系。对比阵元 1、3与阵元1、2的曲线,可以看出由于阵元间距增大会加速SFC的衰落;EVS阵列相比SSA阵列衰落系数幅度更低,并且波动更小,说明EVS阵列能够有效抑制多径信道相关特性,并因此改善系统性能。

图2 URA和EVS-URA在MEOA、MAOA等于90°且ES、AS等于30°时的SFC
图3给出天线阵列在d/λ等于0.5,AS和ES等于30°时空间衰落相关性与MAOA和MEOA的关系,其中EVS阵列取空间极化分量 1、2、6,并将对应天线阵元(a,b)间的 SFC表示为 ρ(a,b,1,1)、ρ(a,b,1,2)和 ρ(a,b,1,6)。

图3 URA和EVS-URA在ES、AS等于30°时的SFC
由图中可以看出阵列的相关性曲面均关于仰角θ= 90°左右对称,且在90°处达到最大;方位角 φ的变化对于相关性的影响比θ更大。引入EVS后,除了ρ(a,b,1,1)与ρ(a,b)近似,其他空间极化分量组合在相关性上有着明显的不同,且均带来相关特性的显著改善。
4.2信道容量
图4给出在d/λ等于0.5、AS和ES等于30°时信道容量与MAOA和MEOA的关系。由图可以看出,URA阵列信道容量关于φ、θ均呈对称趋势,并在对称中心容量达到最大;在θ为0或者180°附近,信道容量基本不受φ变化的影响。EVS阵列相比SSA阵列均增加了约3倍的信道容量,极大地优化了系统的性能。综上表明,EVS阵列性能明显优于SSA阵列。
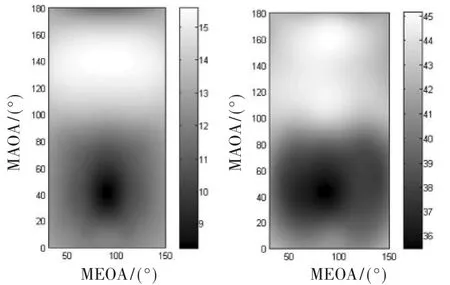
图4 URA和EVS-URA在ES、AS等于30°时的信道容量
5 结语
本文建立了URA小型天线阵列模型,并将EVS单元与其相结合,推导出空间衰落相关性的表达式,并利用相关矩阵计算出信道容量。最后通过一系列的仿真模拟,得到了与理论推导符合的结果。天线阵元数量的增加能够有效提高MIMO系统的性能,但是阵元间的相关性和互耦效应以及空间极化效应则会导致信道容量的下降。采用EVS的天线阵列能够有效缓解多径信道的相关特性,从而使信道容量显著增加,因此EVS天线阵列具有优异的性能和良好的应用前景。
[1]SALZ J,WINTERS J H.Effect of fading correlation on adaptive arrays in digital mobile radio[J].IEEE Transactions on Vehicular Technology,1994,43(4):1049-1057.
[2]TSAI J A,BUEHRER R B,WOERNER B D.Spatial fading correlation function of circular antenna arrays with laplacian distribution energy[J].IEEE Communication Letters,2002,6 (5):178-180.
[3]EGGERS P C F,KOVACS I Z,OLESEN K.Penetration effects on XPD with GSM 1800 handset antennas,relevant for BS polarization diversity for indoor coverage[C].Vehicular Technology Conference,1998.VTC 98.48th IEEE.IEEE,1998,3:1959-1963.
[4]FOSCHINI G J,GANS M J.On limits of wireless communication in a fading environment when using multiple antennas[J].Wireless Personal Communications,1998,6(3):311-335.
[5]IOANNIDES P,BALANIS C.Uniform circular and rectangular arrays for adaptive beamforming applications[J].Antennas and Wireless Propagation Letters,IEEE,2005,4:351-354.
[6]YONG S K,THOMPSON J S.Three dimensional spatial fading correlation models for compact MIMO receivers[J]. IEEE Transactions on Communications,2005,4(6):2856-2869.
[7]ZHOU J,SASAKI S,MURAMATSU S,et al.Spatial correlation for a circular antenna array and its applications in wireless communication[C].Global Telecommunications Conference,2003.GLOBECOM′03,IEEE.IEEE,2003,2:1108-1113.
[8]YONG S K,THOMPSON J S.A 3-Dimensional spatial fading correlation model for electromagnetic vector sensors[A]. IEEE International Symposium on Antennas,Propagation and EM Theory[C].Beijing,China,2003:843-847.
Analysis of MIMO system based on electromagnetic vector sensor
Li Junsong,Zhou Jie
(College of Electronic&Information Engineering,Nanjing University of Information Science and Technology,Nanjing 210044,China)
For the sake of a better performance of multiple input multiple output(MIMO)wireless communication system,a uniform rectangular array based on scalar sensor is developed,and electromagnetic vector sensor(EVS)signal processing method is introduced to the traditional MIMO signal processing method to build up a antenna array based on EVS.Each antenna array′s spatial fading correlation(SFC)closed-form expression is derived to analyze the influence of different angle parameters.Correlation covariance matrixes of both transmitting and receiving terminals are established for analysis of channel capacity of different antenna arrays.By simulating,it′s proved that antenna arrays based on EVS have a better performance as well as application prospect.
multiple input multiple output;antenna array;electromagnetic vector sensor;spatial fading correlation;channel capacity
TN911.6
A
10.16157/j.issn.0258-7998.2015.10.023
国家自然科学基金面上项目(61372128);江苏省科技支撑计划(工业)项目(BE2011195)
2015-04-20)
李峻松(1990-),男,硕士研究生,主要研究方向:移动通信理论、MIMO信道建模等。
周杰(1964-),男,教授,博士生导师,主要研究方向:移动通信理论、无线传感网和无线接入网等。
中文引用格式:李峻松,周杰.电磁矢量传感器EVS对MIMO多天线系统影响研究[J].电子技术应用,2015,41 (10):84-87.
英文引用格式:Li Junsong,Zhou Jie.Analysis of MIMO system based on electromagnetic vector sensor[J].Application of Electronic Technique,2015,41(10):84-87.

