利用PP法简化液体姿轨控发动机化学反应机理

王大锐，程圣清，张 楠

（北京航天动力研究所，北京100076）

0 引言

近年来，耦合详细化学反应的液体火箭发动机燃烧过程研究成为热点，掌握主要推进剂组合的化学反应机理是开展该研究的基础。目前，甲基肼（MMH）/四氧化二氮（NTO）,液氢（LH2）/液氧（LO2）和煤油（Kerosene）/液氧（LO2）是3种主要的航天推进剂组合。与后两种推进剂组合相比，MMH/NTO属于自燃推进剂，其详细机理很难获得。此前，对于此类推进剂组合火箭发动机燃烧CFD计算通常采用总包反应代替，如O.Knab将四步总包反应加入到发动机燃烧模型中[1]，对400 N液体姿轨控火箭发动机燃烧过程进行了数值模拟。研究后发现，总包反应对于中间反应忽略过大，数值计算结果与试验测量结果出入较大，因此需要构建详细机理对发动机燃烧过程进行模拟，其中Laurent构建了一套含有82种组分和403步基元反应的详细机理（机理未公布）[2-3]，该机理通过与Seamans的爆炸理论在点火延迟时间上计算结果的比较[4]，验证了该机理的正确性，但该机理过于复杂，并不适合耦合在湍流场中进行发动机燃烧CFD计算。因此，需要将详细机理进行适当简化，以满足发动机燃烧CFD计算要求。

目前对于复杂燃烧机理的简化大体可以分为2大类，一类是以去除影响较小的基元反应来进行简化，如敏感性分析法SA[5-6]，准稳态假定QSSA[7]，主成分分析法PCA[8-9]等；另一类则是以去除不重要的组分来进行简化，如直接关系图法DRG[10]以及多代通量法PFA[11-12]等。以上各简化方法各有优势，但也都有局限性。

本文提出将PCA和PFA方法联合在一起使用，对43种组分和201步基元反应的甲基肼/四氧化二氮反应机理进行简化研究，并将简化机理与国外文献以及详细机理在典型工况下点火延迟时间、平衡温度以及主要平衡产物计算结果进行对比。最后，对比不同简化方法对MMH和NTO，CH4和O2以及H2和O2三种推进剂组合化学反应机理的简化结果，说明PP法简化效果更好，适用范围更广。

1 主成分联合多代通量机理简化方法

“第一步简化”先对含有m种组分和p步基元反应机理的速度敏感性系数矩阵，其形式如下所示：

矩阵F由下式计算得到：

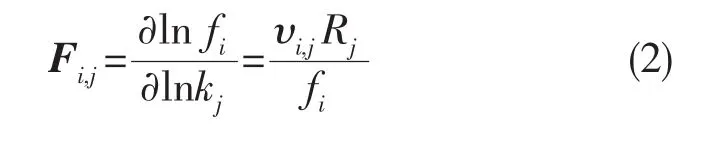
其中

Rj=kjrj(c)

式中：fi为组分i的生成速率；kj为第j步反应的反应速率常数；υi,j为基元反应j中组分i的化学计量系数；Rj为第j步反应的生成物的生成速率；rj(c)为第j步反应中反应物浓度的乘积；Fi,j为第j步反应中组分i的生成或者消耗速率与组分i的净生成率的比值。再将FTF对角化，得到矩阵

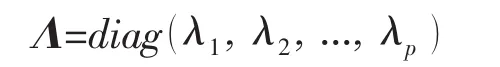
式中λ1,λ2,...,λp为FTF的特征值，且λ1>λ2>...>λp。根据主轴定理，有：

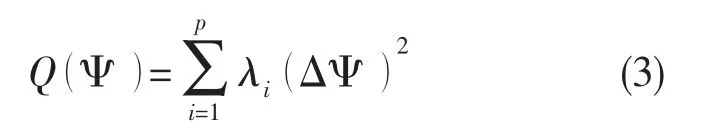
式中：λi为主成分Ψi中各基元反应的重要性，即λi大所对应的特征向量中，元素越大其代表的基元反应越重要。此时，给定简化机理基元反应个数p1，并要求第一步简化后机理的着火延迟时间和平衡温度以及重要组分百分比与原机理计算结果在一定误差之内，具体表达式如下：

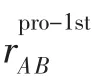
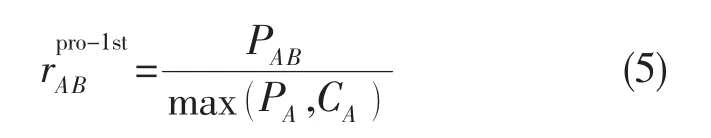
式中：PAB为组分B相对于A的生成相关系数；PA和CA分别为组分A的生成通量和消耗通量。类似地，二代和三代相关系数表达式如下：

式中Mi1和Mi2为中间组分。

从文献 [12]上可以知道，理论上代数越多，简化结果越好，但通过对GRI-Mech3.0机理简化结果来看，四代计算精度提高并不明显，所以本文仍采用三代通量计算来进行简化。最后定义rAB为组分B对组分A的一代、二代及三代相关系数相加之和，表达式如下：

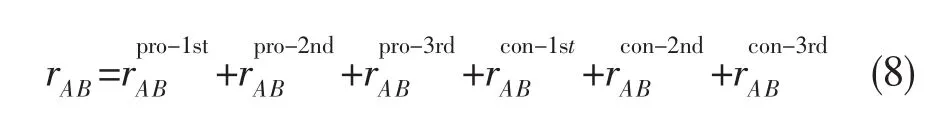
判断组分B对A的重要程度时，将rAB与设定的阈值ε作比较，如果大于该阈值，则认为该组分对组分A重要，予以保留，否则在简化机理时应予以剔除。当全部对A重要的其他组分被找到后，再以这些组分替换A，按照上面的方法继续寻找对该组分重要的其他组分，直到最后一次寻找重要组分时没有找到新的重要组分为止，将此时得到的简化机理2带入式 (4)等验证，验证后的简化机理作为PP方法的最终简化结果。

2 简化结果与分析

本文详细反应机理MN-Detailed包含43种组分201步基元反应，动力学参数参考文献 [13]，热力学参数参考Burcat热力学库[14]，燃烧数值求解由Chemkin软件完成，简化机理由自编程序PP-Beta计算得出。

2.1 简化机理与文献计算结果对比

首先对比详细机理和简化机理与其他文献计算结果。采用Chemkin封闭全混均质反应器对甲基肼/四氧化二氮自燃着火过程进行模拟，模拟反应工况为初始温度为T=298 K，初始压力为p=242×104Pa，定容燃烧，得到不同机理着火温度曲线如下图1所示。

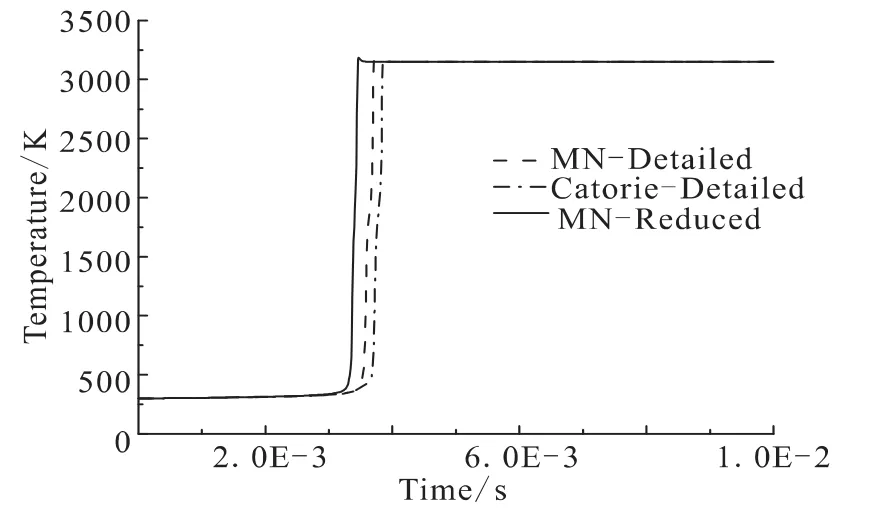
图1 不同机理着火过程温度对比Fig.1 Comparison of temperature in combustion process of different mechanisms

图1中实线为PP法简化结果MN-Reduced机理着火曲线，该机理着火延迟时间为3.33 ms；虚线为MN-Detailed机理着火曲线，着火延迟时间为3.5 ms；点划线为Catorie利用量子化学得到的Catorie-Detailed机理[2]，着火延迟时间为3.82 ms；Seamans利用爆炸理论计算结果为 3.6 ms[4]，MN-Detailed机理和MN-reduced机理着火延迟时间与量子化学详细机理和爆炸理论计算的结果符合较好。

为进一步验证简化结果的正确性，对比了不同压力、不同混合比、不同初温下MN-Reduced机理与Seamans根据爆炸理论着火延迟时间计算的结果，如图2所示其中离散点为MN-Reduced机理计算结果。在温度和混合比一定情况下，着火时间随着压力成负指数下降，而MN-Reduced机理计算压力对着火时间影响规律与Seamans理论计算结果也符合较好。

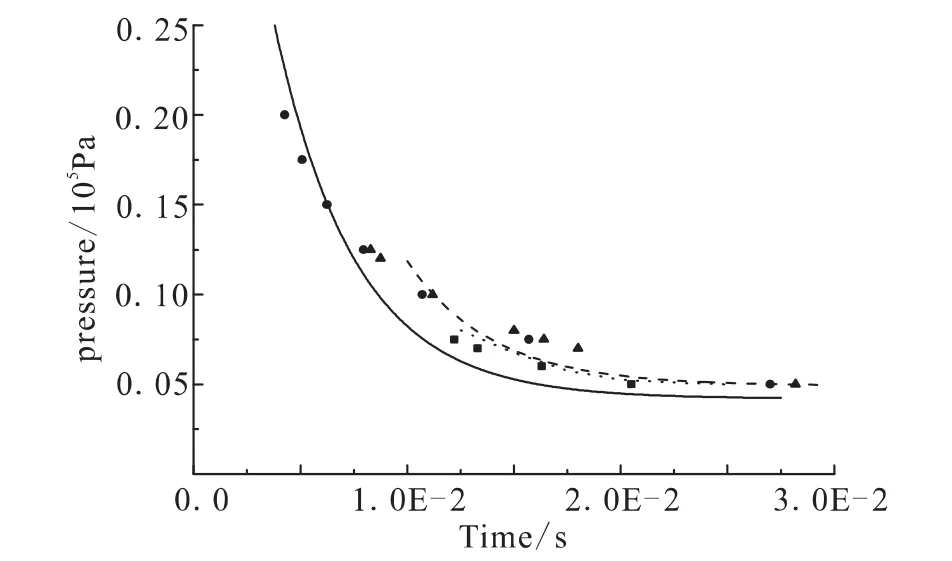
图2 不同压力下着火延迟时间对比Fig.2 Comparison of ignition delay time at different pressure

2.2 发动机特定燃烧工况下PP法简化结果与原机理计算结果比较

要将甲基肼/四氧化二氮简化机理运用到液体火箭发动机燃烧CFD中，还需要比较简化机理与原详细机理在发动机燃烧典型工况下的计算结果。液体火箭发动机燃烧是定压燃烧过程，所以着火过程采用封闭全混均质反应器，求解器采用定压求解。表1中Φ为氧化剂和推进剂质量比。

表1 不同压力下推进剂燃烧初始条件Tab.1 Initial conditions of propellant combination combustion at different pressure

表1和图3是对初始温度一定、混合比一定时，不同压力下简化机理与详细机理对着火延迟时间和平衡温度计算结果的对比。可以看出，简化机理与详细机理在不同压力下着火过程均符合较好，着火延迟相差均在3×10-5s以内，平衡温度相差0.1 K以内。

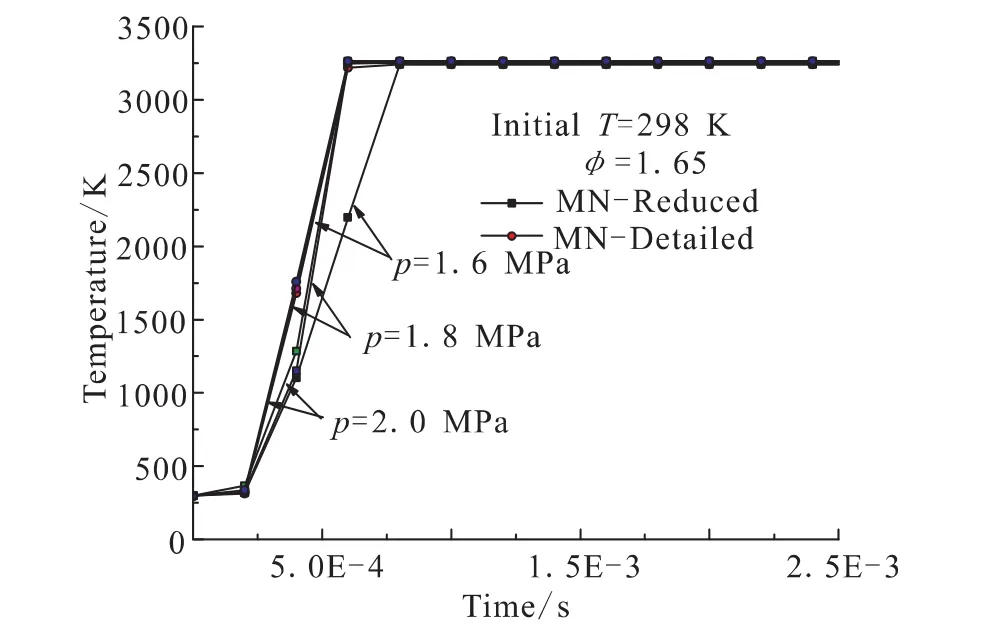
图3 不同压力下简化机理和详细机理着火过程比较Fig.3 Combustion process comparison of simplified mechanism and detailed mechanism at different pressure

表2和图4是对初始温度一定、燃烧压力一定，不同混合比下简化机理与详细机理对着火延迟时间和平衡温度计算结果的对比。可以看出，简化机理与详细机理在不同混合比下着火过程均符合较好，着火延迟相差均在2×10-5s以内，平衡温度相差0.1 K以内。

表2 不同氧燃比下推进剂燃烧初始条件Tab.2 Initial conditions of propellant combination combustion at different mixing ratio

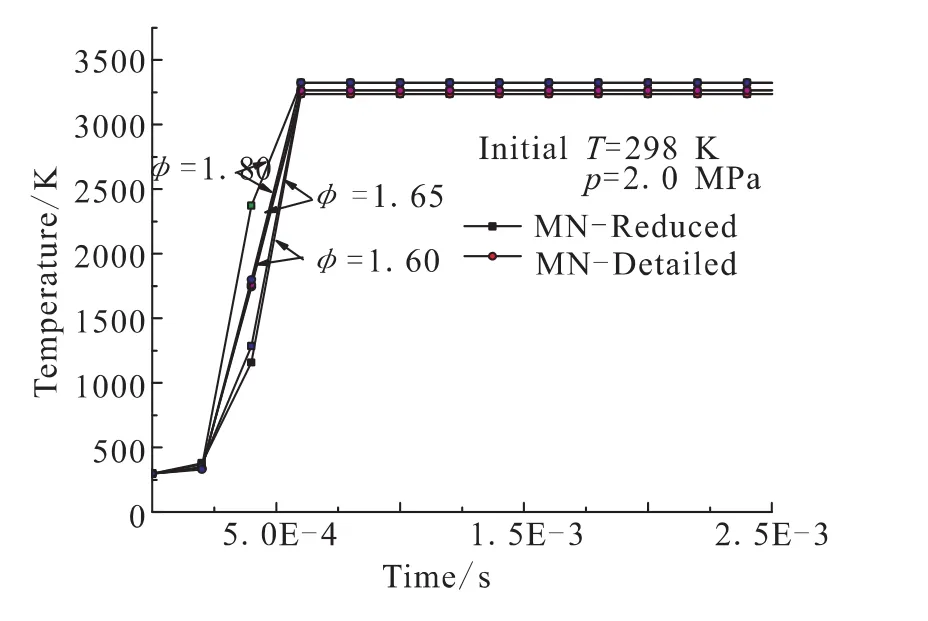
图4 不同氧燃比下简化机理与详细机理燃烧过程比较Fig.4 Combustion process comparison of reduced mechanism and detailed mechanism at different Φ

图5 不同压力下简化机理与详细机理H2O摩尔百分数计算结果对比Fig.5 Comparison of H2O mole fraction calculation results of simplified mechanism and detailed mechanism at different pressure

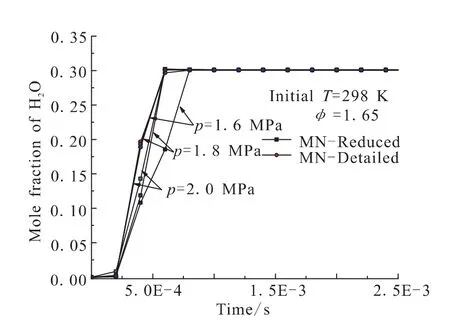
图6 不同压力下简化机理与详细机理N2摩尔百分数计算结果对比Fig.6 Comparison of N2mole fraction calculation results of simplified mechanism and detailed mechanism at different pressure

图5和图6是质量混合比1.65，初始温度298 K，不同压力下主要平衡产物H2O和N2简化机理和详细机理计算结果的对比。可以看出，整个着火过程中简化机理计算结果与详细机理计算结果均符合较好。

综上，利用PP法得到的简化机理在着火延迟时间、平衡温度以及平衡组分摩尔百分数都与详细机理计算结果保持很好的一致性，这为耦合MMH/NTO化学反应的发动机燃烧CFD研究奠定了良好的基础。

2.3 PP法与主成分分析和多代通量方法的比较

主成分法 (PCA)和多代通量分析法 (PFA)都是比较常用的化学反应机理简化方法，但各自在使用时均有一定的局限性，本文采用PCA，PFA 及 PP法对MMH/NTO，H2/O2[14]及CH4/O2[15]推进剂化学反应详细机理进行简化，对比简化结果如表3所示。

表3中，MMH/NTO详细机理在质量混合比1.6～1.8，压力 1.6～2.0 MPa，初始温度 298 K 范围内简化；H2/O2详细机理在摩尔混合比1～4，压力0.1～1 MPa，着火温度为1 000 K范围内简化；CH4/O2详细机理在摩尔混合比1～2，压力0.1～1 MPa,着火温度为1 300～1 500 K范围内简化。从表3中可看出：一方面PCA简化机理结果基元反应数少于PFA简化结果，但组分种类要明显多于PFA，这是因为PCA通过去除非重要基元反应达到简化详细机理目的，而PFA则是通过去除非重要组分种类来简化详细机理，PP法将它们的特点结合起来，既能够去除非重要基元反应又能够去除非重要组分，因而得到更为简单的简化机理；另一方面，从H2/O2和CH4/O2简化结果来看，PCA、PFA存在一定局限性，只能对一部分推进剂反应机理进行简化，而PP法可以简化机理的范围比前两者都大，具有发展成一种通用简化方法的潜力。

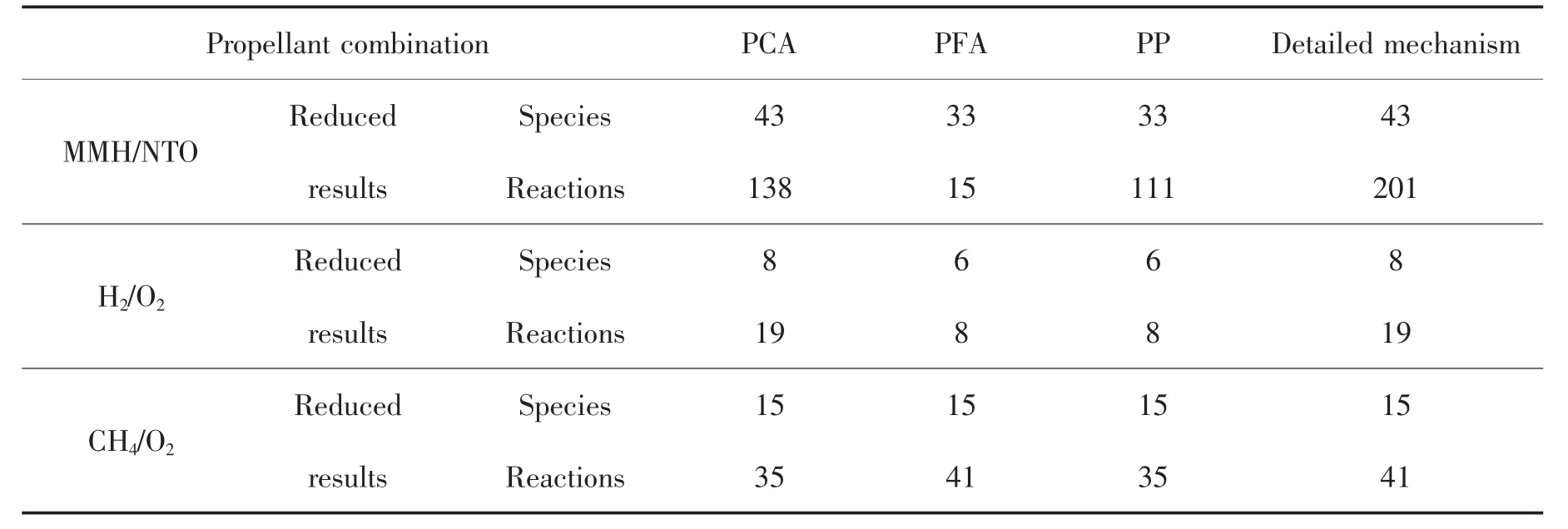
表3 不同简化方法对3种推进剂组合简化结果对比Tab.3 Comparison of simplified results of three combined propellants using different simplification methods

3 结论

本文运用PP方法对MMH/NTO推进剂组合43种组分201步基元详细机理进行了简化，简化机理与国外文献以及详细机理在多种典型工况下着火延迟时间、平衡温度以及平衡组分摩尔百分数计算结果都符合较好，说明简化机理可以有效代替详细机理进行燃烧计算，并为进行耦合化学反应的液体姿轨控火箭发动机燃烧CFD研究奠定了良好基础；PP方法相比于PCA和PFA方法具备可同时减少基元反应个数和组分种类的特点，简化效果好，简化机理适用性也更广。

[1]KNAB O,PRECLIK D,ESTUBLIER D.Flow field prediction within liquid film cooled combustion chambers of storable bipropellant rocket engines,AIAA 98-3370[R].USA：AIAA,1998.

[2]CATOIRE L,CHAUMEIX N,PAILLARD C.Chemical kinetic model for monomethylhydrazine/nitrogen tetroxide gas-phase combustion and hypergolic ignition[J].Journal of Propulsion and Power,2004,20(1)：87-92.

[3]CATOIRE L,SWIHART M T.Thermochemistry of species produced from monomethylhydrazine in propulsion andspace-relatedapplications[J].Journal ofPropulsion and Power,2002,18(6)：1242-1252.

[4]SEAMANS T F,VANPEE M,AGOSTA V D.Development of a fundamental Model of hypergolic ignition in space-ambient engines[J].AIAA Journal,1967,l5(9)：1616-1624.

[5]TURANYI T,BERCES T,VAIDA S.Reaction rate analysis of complex kinetic system[J].International Journal of Chemical Kinetics,1989,21(2)：83-99.

[6]乔瑜,徐明厚.基于敏感性分析的甲烷反应机理优化简化[J].华中科技大学学报(自然科学版),2007,35(5)：85-87.

[7]PETERS N,WILLIAMS F A.The asymptotic structure of stoichiometric methane-airflame[J].Combustion and flame,1987,68(2)：185-207.

[8]LU T F,CHUNG K L.A directed relation graph method for mechanism reduction[J].Proceedings of the Combustion Institute,2005,30：1333-1341.

[9]VAJDA S,VALKO P,TURANYI T.Principle component analysis of kinetic model[J].International Journal of Chem-Kinet,1985,17：55-81.

[10]董刚,邱榕,蒋勇,张和平.利用主成分分析法简化甲烷/空气层流预混火焰的反应机理[J].火灾科学,2004,13(3)：158-162.

[11]SUN W T,CHEN Z,GOU X L,et al.A path flux analysis method for the reduction of detailed chemical kinetic mechanisms[J].Combustion and Flame,2010,157(7)：1298-1307.

[12]苟小龙,王卫,桂莹,施万玲.一种多代路径通量分析化学机理简化方法[J].推进技术,2012,33(3)：412-417.

[13]ANDERSON W R.,MCQUAID M J,MICHAEL J,et al.A detailed,finite-rate,chemical kinetics mechanism for monomethylhydrazine-red fuming nitric acid systems,ARL-TR88-502010[R].[S.l.]：ARL-TR,1988.

[14]MATSUO A,FUJII K,FUJIWARA T.Flow features of shock-induced combustion around projectile traveling at hypervelocities[J].AIAA Journal,1995,33(6)：1056-1063.

[15]YANG B,POPE S B.An investigation of the accuracy of manifold methods and splitting schemes in the computational implementation of combustion chemistry[J].Combustion and Flame,1998,112：16-32.

[16]聂万胜,丰松江.液体姿轨控火箭发动机燃烧动力学模型与数值模拟[M].北京：国防工业出版社,2011.