一类七次系统幂零奇点的中心判定
卜珏萍 陶有田
(巢湖学院应用数学学院,安徽 巢湖 238000)
一类七次系统幂零奇点的中心判定
卜珏萍 陶有田
(巢湖学院应用数学学院,安徽 巢湖 238000)
研究了一类七次系统三次幂零奇点的中心判定问题。利用Mathematica软件进行计算并化简,推导出该七次微分系统原点的前9个拟Lyapunov常数,并在此基础上进一步分析讨论,从而得出原点成为中心的充要条件。
七次系统;幂零奇点;中心;拟Lyapunov常数
讨论一类特殊的七次微分自治系统
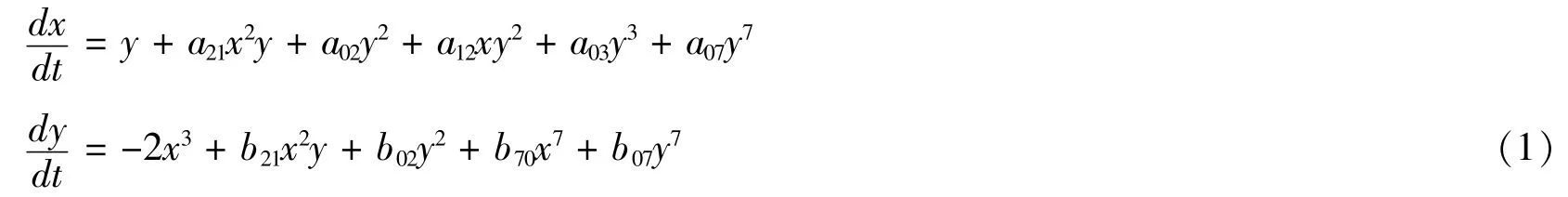
的中心判定问题。其中,原点为三次幂零奇点。由文献[1],系统(1)的原点为中心或焦点。
由文献[3],对系统(1)可待定形式级数M(x,y)=y2+x4+o(r4)与正整数s使得成立。另由文献[3]中的递推公式

在Mathematica上计算并化简得

因为s是正整数,故可得系统(1)原点的前两个拟Lyapunov常数

以下取s=1,并在Mathematica软件上进一步计算可以得到:
定理1 系统(1)在原点的前9个拟Lyapunov常数分别为:

由λi=0(i=1,2,…,9)时,可得
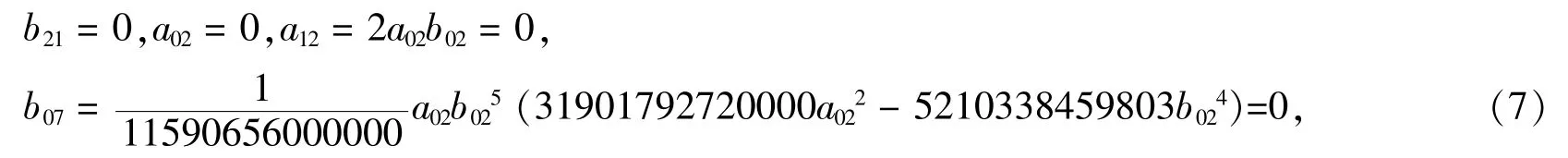
或

故由式(7)与(8),得
定理2 系统(1)的原点前9个拟Lyapunov常数全部为零,即:

条件(9)与(10)其中之一成立。
(i)当式(9)成立时,系统(1)可化为
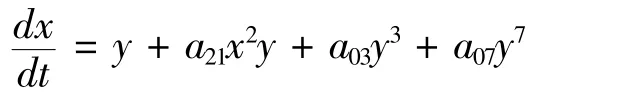

此时,
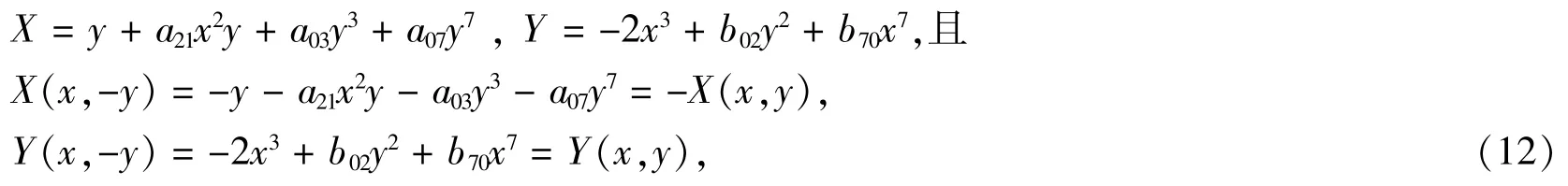
因此由对称原理,系统(1)的向量场对称于x轴,并且原点为中心。
(ii)当式(10)成立时,系统(1)可化为

此时,
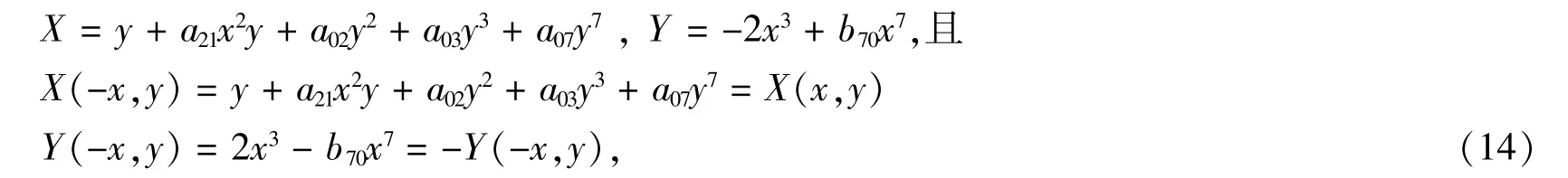
因此由对称原理,系统(1)的向量场对称于y轴,并且原点为中心。
根据以上分析得:
定理3 系统(1)的原点成为中心的充要条件是原点的前9个拟Lyapunov常数全部为零,即条件(9)与(10)其中之一成立。
[1]Amelikin.B.B.,Lukashivich.H.A.&Sadovski.A.P.Nonlinear Oscillations in Second Systems[M].BGY Lenin∶B.I.Press,1982.
[2]刘一戎,李继彬.平面向量场的若干经典问题[M].北京:科学出版社,2010.
[3]Alvarez.M.J.&Gasull.A.Cenerating limits cycles from a nilpotent critical point via normal forms[J].J.Math.Anal.Appl.,2006∶271-287.
[4]Liu,Y.R.Theory of center-focus in a class of high order singular points and infinity[J].Sci.in China,2001,(1)∶37-48.
[5]Zhang Qi&Liu Yirong.A cubic polynomial system with seven limit cycles at infinity[J].Applied Mathematics and Computation,2006,(1)∶319-329.
[6]赵倩倩.一类原点为幂零奇点的七次系统的中心判定[J].科技信息,2012,(3)∶301-302.
[7]卜珏萍.一类七次系统三次幂零奇点的中心判定[J].大庆师范学院学报,2014,(6)∶33-35.
ON THE CRITERION OF THE CENTER FOR NILPOTENT SINGULAR POINTS IN A CLASS OF SEVEN-ORDER SYSTEM
BU Jue-ping TAO You-tian
(School of Applied Mathematics,Chaohu College,Chaohu Anhui 238000)
The criterion of the center for three-order nilpotent singular points in a class of seven-order system is studied in this paper.The software,Mathematica,is used to calculate and simplify to derive the first nine quasi-Lyapunov constants of the origin of this differential system.Based on this,we have further discussion and analysis to obtain the necessary and sufficient conditions which make the origin center.
seven-order system;Nilpotent singular point;center;quasi-Lyapunov constant
O175
A
1672-2868(2015)06-0007-03
责任编辑:陈 侃
2015-10-17
巢湖学院院级自然科学研究项目(项目编号:XLY-201401);巢湖学院院级自然科学研究项目(项目编号:XLY-201502);安徽省高校优秀青年人才支持计划重点项目(项目编号:gxyqZD2016285)
卜珏萍(1985-),女,安徽巢湖人。巢湖学院应用数学学院,讲师。研究方向:微分方程定性理论与分支问题。

