颜面赝复体与周围组织的几何及纹理光顺过渡方法研究
颜面赝复体与周围组织的几何及纹理光顺过渡方法研究
孙进1,2,朱兴龙1, 陈晓波2, 曹肖伟1
(1.扬州大学 机械工程学院,江苏 扬州225127;2.上海交通大学 计算机集成制造研究所,上海200240)
摘要:基于面结构光数据特点对颜面赝复体与周围组织的几何及纹理光顺过渡方法进行了研究.利用隐函数来表征颜面赝复体与周围组织的3D模型,并且对两者的间隙进行重新三角化和伞形迭代运算,实现两者交界处的平滑过渡;利用带有像素和纹理信息的面结构光点云数据实现精确纹理映射,求解过渡区域颜色场的泊松系统方程,获取能够最佳拟合梯度的颜色场,实现两者交界处纹理的光顺过渡,避免纹理映射中的光照不均现象和纹理接缝现象.
关键词:颜面赝复体;几何建模;贴合;纹理;过渡面
收稿日期:2015-04-17
基金项目:国家自然科学
基金项目江苏省博士后(1302179C);扬州市|扬州大学科技合作资金项目(2012038|12)
作者简介:孙进(1973-),男,江苏扬州人,讲师,博士,硕士生导师,主要从事三维视觉医学测量建模研究.
中图分类号:TP391.72文献标志码:A
利用颜面赝复体能够有效恢复患者的颜面外观.实现颜面赝复体与周围组织的几何及纹理光顺过渡有两个目的:1)佩戴舒适美观,一个好的颜面赝复体应该能够与患者的外观很好的贴合,这样使得患者佩戴舒服,并能体现其美学效果;2)效果可视化,如果缺乏颜面赝复体的逼真可视化,那么患者与医生之间就很难实现互动来确定他最终所需要的效果.因此,这样的问题转化成逆向工程的理论描述就是:如何通过赝复体边缘部分的几何设计和纹理设计来实现赝复体与周围组织的几何及纹理光顺过渡.
1 几何光顺技术
1.1几何光顺准则
连接两个或多个曲面的过渡曲面(blending surface)的几何光顺准则,通常是根据曲面上的关键曲线是否光顺以及曲面的曲率(主曲率、高斯曲率、平均曲率等)的变化是否均匀来判断[1].
1.2几何光顺方法
1) 神经网络法.2009年蒋刚[2]采用向量机分别对经空间映射获得的三方向二维坐标进行回归运算,获得构建过渡曲面所需要的三维点坐标值.2) 利用影响区域数据法.2005年陈志杨等[3]利用影响区域内的数据构造连续曲面和过渡区域内数据点.2004年Funkhouser等[4]在源网格(牛头)与目标网格(羊身)的边界线实现两者的光顺过渡.3)基于偏微分方程(PDE)过渡.2009年王烈等[5|6]基于热传导方程分别研究了变动边界和固定边界情况下的过渡面构造.4)基于能量优化法过渡.2004年Luo等[7]提出了基于能量模型增加时间变量的动态NURBS曲面的构造.5)双伞形算子.2007年Chen[8]提出了双伞形算子概念:先建立每个顶点的伞形算子并计算它在法向的位移,通过迭代使得该位移值趋于零;Fu等[9]用类似的方法完成了不同数据之间的融合.在这些算法中,神经网络方法避开了数学函数的非线性计算,但需要一定量的表面点数据作为支撑;基于周边信息的方法能够与周边区域光顺过渡,但需要确定影响区域的位置;PDE法需要给定边界及其跨界导矢条件,且对于一般自由曲面并不适合;双伞形算子法在保证较好的初始边界条件下,能够实现局部区域的平滑过渡.
2 纹理光顺技术
2.1纹理光顺概念
受到相机视角大小的限制,获取一幅完整的数据往往需要多视角视图拼合.物体不同视图的同一部位因光照等因素导致其颜色值并不相同.这就会造成两个现象:1)由于相机曝光和灯光条件不同,在一组拼合扫描数据重叠区造成颜色过渡不连续,甚至产生接缝现象;2)当纹理映射到几何模型上时,颜色信息与点的信息不能一一对应导致的纹理变形现象.因此,纹理光顺需要实现两个目标:最终带纹理映射的几何模型不出现明显的接缝现象,尽量降低生成图像与原始图像的失真度.
2.2纹理光顺方法
1)特征点的映射方法.2008年Ohkubo等[10]从自动抽取模型表面的三维边缘特征入手,进行特征对应的寻找.2)分块组合方法.2004年Zhao等[11]基于网格模型分块视角相关纹理映射的原理实现了人脸的逼真可视化.3)搜索最优缝合路径的方法.2006年Li等[12]通过小波分解技术将原始图像集合分为边缘图和平滑图,对边缘图像采用图像缝合法进行拼接,提出了在部分纹理图表面搜索最优缝合路径的方法,对平滑图像采用多尺度融合法拼接.4)重叠区设置权重的方法. 2008年Ding等[13]提出一种为三维物体表面添加精确纹理的方法,三维光学数字成像系统可同时采集物体在同一个方向的深度图像和与它精确对应的纹理图像,可以在深度图像合成的同时进行纹理图像的融合.5)用颜色梯度场的方法.2004年Su等[14]和Levin等[15]通过在2D图像域定义加权函数来降低图像差异对视图融合的影响.2009年Chuang等[16]将梯度域的方法延伸到三角网格上来,首先通过在每个视图上添加颜色梯度获取一个描写纹理细节变化的颜色梯度场,然后求解梯度场的泊松方程,得到能够最佳拟合梯度变化的颜色场,将颜色场映射到几何模型上,可以得到一个无缝的纹理表面.
在这些算法中,基于特征点的映射方法优点是计算量小,但特征点准确性影响纹理映射变形程度;基于分块组合的方法仅需对需要过渡部分进行处理,但它要求有三幅正交的人脸图像;搜索最优缝合路径的方法在消除接缝的同时能够最大限度保存图像原有细节信息,但仅适合形状简单模型;重叠区设置权重方法由于权值是人为设定,无法保证纹理平滑过渡;用颜色梯度场的方法可得到一个无缝纹理表面,保证纹理的平滑过渡,但须增加颜色梯度场计算.
3 融合面结构光点云特点的几何及纹理光顺技术
3.1面结构光点云特点
如图1所示,面结构光扫描仪将二维模板投射到3D物体上,然后用相机获取这个图像,再利用三角化原理得到三维点的坐标,因此,可以获取带纵横像素信息的点云.点云的每个点包含有5个数据x,y,z,pc,pr.x,y,z为点在空间的3个坐标,pc和pr分别表示点横坐标和纵坐标方向的像素值.一个面结构光图像的像素产生一个测量点,即点与像素是一一对应的,通过每个采样点所处的行和列编号,则可知此点的纹理信息,达到纹理图像与深度图像精确的对应.因此,点的信息可设计为图2:x,y,z,R,G,B,pc,pr,其中R,G,B值是该点的颜色值.其优点是将点的信息从三维空间上升到纹理空间,使用同一个变换矩阵可使点三维坐标与纹理坐标同时变换,实现了纹理精确映射[17].
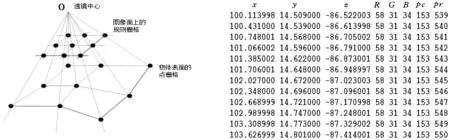
图1 3D点云与2D像素一一对应 图2 自定义点结构
3.2几何光顺算法
1)删除操作.我们使用隐函数技术来进行删除操作.隐函数有下列表达形式:P(X,Y,Z)=C(C为常量) . 例如,一个半径为R,球心在原点的球S用方程P(X,Y,Z)=C表达.即P(X,Y,Z)=R2-X2-Y2-Z2.当P(X,Y,Z)=0,该方程精确表达了球S,而P(X,Y,Z)<0则描述了在球S外面的部分.
2)对源数据和目标数据之间形成的间隙部分进行重新三角化.
3)进行伞形迭代,对不规则的三角形进行规则化,实现几何平滑,如图3所示.总曲率是表面平滑的度量,公式如下,这里kmax和kmin是表面的主曲率.
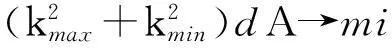
(1)
通过伞形迭代来进行总曲率最小化[18]:
P′=P-λ[U2(p)-(U2(p)·Np)·Np],
(2)
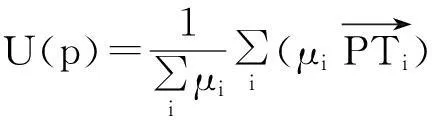
(3)
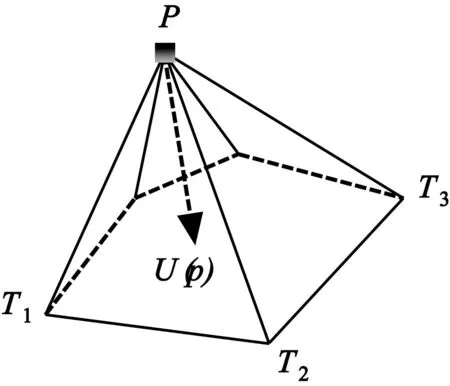
图3 网格顶点P的伞形算子
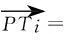
3.3纹理光顺算法
纹理光顺算法原理是将多视纹理映射问题转化为解决在一个拼合好的网格上定义每个点颜色值的优化问题.算法步骤如下:
1)获取一组带纹理的网格数据(称为视图),如图4(a),(b).
2)不考虑纹理信息,将这一组网格数据进行多视图对齐和融合,如图4(c).
3)对齐后的数据进行孔洞填充,得到一个基础网格,如图4(d).
4)对基础网格构建初始颜色场,即为基础网格上的每个点确定一个初始颜色值.a.对基础网格和各视图进行栅格划分;b.从基础网格中的每个点t,得到其索引值It;c.根据其索引值It,在各视图中找到相同索引值的点系列Di;d.在Di中找到与点t距离最近的点,并将该点的颜色值赋给点t.
5)得到基础网格优化的颜色场.
通过求解泊松方程可使得a‖f-g‖2+‖f-V‖2最小化,从而得到一个能够最佳拟合梯度的颜色场; g是各视图的颜色场,V是各视图的颜色梯度场,a是描述插值约束重要性权重,f是要求的如图4(d)的基础网格的优化颜色场.
6)将颜色场施加到图4(d)的几何模型上,最终就得到了带有精确纹理信息的几何模型,如图4(e).
本算法与Chuang等[16]方法的不同之一在于增加步骤3)中的孔洞填充,然后利用步骤4),对孔洞填充的数据点搜索到最近点的颜色作为自己的初始颜色,再参与后面的颜色场优化,从而实现了纹理孔洞的填充,保证孔洞区的颜色能够与周边数据光滑过渡;不同之二在于利用栅格搜索结构替代了原有的KD树搜索结构,由于栅格搜索结构的最近点搜索速度为O(Np),而KD树搜索结构的速度为O(NplogNx),Np是固定网格的点数,Nx是与固定网格对齐的移动网格的点数.对于大型的数据来说,很大一部分时间用于最近点的搜索,而采用栅格搜索结构则加快了运算速度.

图4 基于颜色梯度场的纹理映射
4 系统应用
图5所示为一颌面缺损的患者赝复体.按照操作流程,图5(a)是数据预处理,图5(b)是几何光顺,图5(c)是纹理光顺,可以发现赝复体与患者颜面纹理能够光滑过渡.图5(d)是构建的赝复体与患者颜面偏差显示图,可以发现两者交接区域的颜色以青色为主,表明两者的距离偏差低于0.2 mm,可满足临床对赝复治疗的需要.
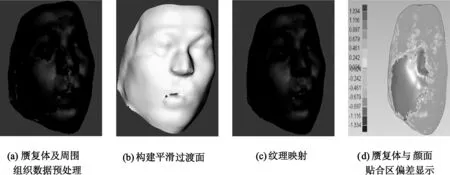
图5 颜面赝复体的构建
5 结语
本文对颜面赝复体与周围组织的几何及纹理光顺过渡方法进行了研究,提出了融合面结构光点云特点的几何及纹理光顺方法.
1)利用隐函数来表征颜面赝复体与周围组织的3D模型,并且对两者的间隙进行重新三角化和伞形迭代运算,实现两者交界处的平滑过渡.
2)带有像素和纹理信息的面结构光点云的三维坐标与纹理坐标能同时应用同一个变换矩阵进行坐标系变换,实现精确纹理映射.
3)求解颜面赝复体与周围组织数据所组成的颜色场泊松方程,得到能够最佳拟合梯度的颜色场,使得恢复颜面赝复体与周围组织数据的过渡曲面的颜色能够光顺过渡,解决了纹理映射中纹理接缝现象以及纹理变形现象.
参考文献:
[1] 朱心雄.自由曲线曲面造型技术[M].北京:科学出版社,2000.
[2] 蒋刚.基于SVM 和空间投影的点云空洞修补方法[J].计算机工程,2009,35(22):269|271.
[3] 陈志杨,张三元,叶修梓.点云数据中空洞区域的自动补测算法[J].计算机辅助设计与图形学学报,2005,17(8): 1793|1797.
[4] Funkhouser T,Kazhdan M,Shilane P,et al.Modeling by example[J].ACM Transactions on Graphics,Proceedings of ACM SIGGRAPH 2004,2004,23(3):652|663.
[5] 王烈,叶正麟,石茂.光顺过渡面的热传导方程|能量优化构造方法[J].数值计算与计算机应用,2009(4):295|304.
[6] 王烈,叶正麟,石茂.具有变动边界的过渡面的热传导方程构造法[J].计算机工程与应用,2009,45(32):133|136.
[7] Luo X,Liu N,Gao C.Fairing geometric modeling based on 4|point interpolatory subdivision scheme[J].Journal of Computational and Applied Mathematics,2004,163(1):189|197.
[8] Chen C Y,Cheng K Y.A sharpness|dependent filter for recovering sharp features in repaired 3D mesh models[J].IEEE Transactions on Visualization and Computer Graphics,2008,14(1):200|212.
[9] Fu H,Au O K C,Tai C L.Effective derivation of similarity transformations for implicit Laplacian mesh editing[J].Computer Graphics Forum,2007,26(1):34|45.
[10] Ohkubo R,Kurazume R,Ikeuchi K.Simultaneous registration of 2D images onto 3D models for texture mapping[M]
//Digitally Archiving Cultural Objects,New York:Springer US,2008:237|278.
[11] Zhao X Y,Du L M.Model smoothing and realistic texture mapping in human face synthesis[J].Journal of Computer|aided Design & Computer Graphics,2004,16(11):1517|1522.
[12] Li X L,Zha H B.Seamless 2D|3D texture mapping[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2006,42(5): 674|680.
[13] Ding Y B,Peng X.Smart method of multiple textures blending and mapping on 3D objects[J].Application Research of Computers,2008,25(1):300|302.
[14] Su M S,Hwang W L,Cheng K Y.Analysis on multiresolution mosaic images[J].IEEE Transactions on Image Processing,2004,13(7):952|959.
[15] Levin A,Zomet A,Peleg S,et al.Seamless image stitching in the gradient domain[J].Computer Vision|ECCV 2004,2004,3024:377|389.
[16] Chuang M,Luo L,Brown B J,et al.Estimating the laplace|beltrami operator by restricting 3D functions[J].Computer Graphics Forum,2009,28(5):1475|1484.
[17] 孙进.非完备几何特征测量数据建模及其在颜面缺损修复中的应用研究[D].上海:上海交通大学,2012.
[18] Sun J,Chen X B,Lu X Y,et al.Research on 3D textured dress geometry modelling[J].International Journal of Clothing Science and Technology,2012,24(2/3):102|117.
Smooth and Texturing Blending Surface Modelling for Marginal
Area of Facial Prosthesis Based on Areal Scan Data
SUN Jin1,2,ZHU Xinglong1,CHEN Xiaobo2,CAO Xiaowei1
(1.College of Mechanical Engineering, Yangzhou University, Yangzhou 225127, China;
2.Institute of Computer Integrated Manufacturing,Shanghai Jiao Tong University, Shanghai 200240, China)
Abstract:The purpose of this paper is to describe how to model the smooth and texturing blending surfaces for marginal area of facial prosthesis adjoined to surrounding tissues based on the characteristics of areal scan data.First in the geometry modelling stage,the implicit function was used in segment 3D models to re|triangulate the resulting gap and umbrella iterations and the smooth transition between facial prosthesis and surrounding tissues can be achieved.Then in the texture mapping stage,a seamless textured surface can be produced quickly based on the method of solving the Poisson equation for the colour field that best fits the colour gradients with a grid search structure.
Key words:facial prosthesis; geometry modelling; smooth; texture; blending surfaces
(编辑武峰)

