分块矩阵广义逆的表示

分块矩阵广义逆的表示

杜法鹏1,2

(1.东南大学 数学系，江苏 南京210096;2.徐州工程学院，江苏 徐州221018)

摘要：文章采用矩阵分解的方法讨论了2×2分块矩阵M=的{1,2}逆，{1,3}逆，{1,4}逆显式表示问题，并利用分块矩阵M的{1,2}逆的表示给出了分块矩阵M的Moore|Penrose逆的显式表达式.

关键词：分块矩阵，广义逆， Moore|Penrose 逆

收稿日期：2015-04-22

基金项目：徐州工程学院培育项目(XKY2014207)

作者简介：杜法鹏(1974-)，男,江苏沛县人，东南大学博士后，徐州工程学院副教授,主要从事算子代数、应用泛函分析、算子广义逆理论研究.

中图分类号：O151.21文献标志码：A

文中记Cm×n为m×n阶矩阵的全体. 广义逆理论是应用十分广泛的数学分支，它在数值线性代数、数值分析、最优化、控制论、微分方程及应用数学等众多领域中有着非常重要的应用.奇异方阵是不可逆的,然而在求解矩阵方程时经常遇到奇异矩阵,特别是在求解最小二乘解或最小范数解得时候，就需要广义逆的概念.

1920年,E.H.Moore将非奇异方阵的逆矩阵推广到任意矩阵上去，引入了广义逆的概念. Moore将满足方程AG=PA，GA=PG的矩阵G∈Cn×m定义为矩阵A∈Cm×n的广义逆[1].其中,PX表示矩阵X列向量张成子空间上的投影. 1955年,R.Penrose用以下4个方程给出了1个等价定义：

AXA=A， XAX=X， (AX)*=AX， (XA)*=XA，

称矩阵X为矩阵A的Mooere|Penrose广义逆(简称MP逆),通常记作为A+[2].由于MP逆与最小二乘解有关，因而得到广泛的研究.

为了不同的应用目的,人们根据不同的条件,引入不同的广义逆. 设A∈Cm×n，X∈Cn×m，考虑以下方程:

(1)AXA=A， (2)XAX=X, (3)(AX)*=AX,

(4)(XA)*=XA, (5)AX=XA， (6)AkXA=Ak,

其中,A*表示A的共轭转置,k正整数.

定义1[3]记A{i,j,…,k}为满足以上方程中第{i,j,…,k}个方程的矩阵X∈Cn×m的全体，矩阵X∈A{i,j,…,k}称为矩阵A的一个{i,j,…,k}逆，记作A{i,j,…,k}.

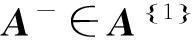
MP逆和Drazin逆是最重要的两类广义逆,也是研究最多的两类广义逆. 本文中主要讨论MP逆的相关问题. 我们知道若MP逆存在,则是唯一的, 由[4, 命题3.5.3]知道下列关系成立：

A†=A*(AA*)+=(A*A)†A*.

下面的引理给出了A-与A†之间的关系：

引理1[5,6]设A∈Cm×n，则有

A†=(I-P-P*)A-(I-Q-Q*)

其中，P=A-A，Q=AA-.

分块矩阵广义逆的表示问题很多文献[3,7,8]都研究过.在文献[7]中R.E.Hartwig借助于Brown|Mccoy引理([7,Lemma 1])在环上给出了2×2分块矩阵广义逆的表示.在文献[8]中，陈永林利用矩阵方程的解给出了2×2分块矩阵{1,2}的表示.在本文中，再次考虑2×2分块矩阵广义逆的表示问题，利用矩阵分解的给出2×2分块矩阵广义逆的显式表达式.

1　预备知识

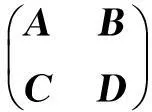
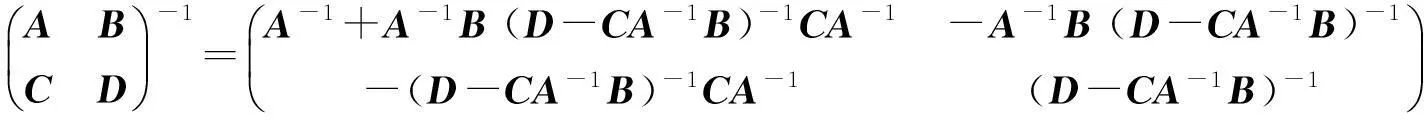
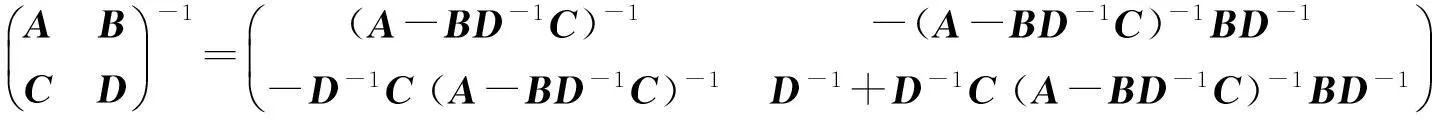
引理3[4,6,10]设S∈Cn×n为幂等矩阵,则I-S-S*可逆.记O(S)=S(S+S*-I)-1,则O(S)2=O(S)=O(S)*(即O(S)为投影).

引理4[7]设A∈Cm×n,则

(1)X为矩阵A的{1,3}逆当且仅当A*AX=A*;

(2)X为矩阵A的{1,4}逆当且仅当XAA*=A*.

引理5设A∈Cm×n,则A-AA-[AA-+(AA-)*-I]-1∈A{1,3}.

证明：记X=A-PR(A)，易知AXA=A及AX=PR(A)，即X∈A-{1,3}，由引理3知PR(A)=O(AA-)=AA-[AA-+(AA-)*-I]-1，因而结论成立.

引理6设A∈Cm×n,则[A-A+(A-A)*-I]-1A-AA-∈A{1,4}.

证明：由引理3知PN(A)⊥=I-O(I-A-A)=[A-A+(A-A)*-I]-1A-A，又PN(A)⊥A-∈A{1,4}，故结论成立.

注：在引理5及引理6中分别将A-换成A+,则A+[AA++(AA+)*-I]-1∈A{1,2,3}以及[A+A+(A+A)*-I]-1A+∈A{1,2,4}.

引理7设A∈Cm×n，则矩阵A的任何一个{1,3}逆X都可以表示成

X=A{1,3}+(I-A{1,3}A)Z,

其中，A{1,3}为任意固定的一个{1,3}逆, Z∈Cn×m为任意矩阵.

证明：由引理4(1)知

X=(A*A)-A*+Z-(A*A)-A*AZ,

又(A*A)-A*∈A{1,3}，故结论可得.

引理8设A∈Cm×n，则矩阵A的任何一个{1,4}逆X都可以表示成

X=A{1,4}+(I-AA{1,4})Z，

其中，A{1,4}为任意固定的一个{1,4}逆, Z∈Cn×m为任意矩阵.

证明：由引理4(2)可得.

引理9设X,Y∈Cm×n且X+Y=YX+=0， 则G=X++(I-X+X)Y+(I-XX+)为X+Y的一个{1,2}逆，此时，

(X+Y)G=XX++YY+(I-XX+)， G(X+Y)=X+X+(I-X+X)Y+Y.

证明：由X+Y=YX+=0知Y(I-X+X)=Y=(I-XX+)Y,简单计算可知

(X+Y)G=XX++YY+(I-XX+)， G(X+Y)=X+X+(I-X+X)Y+Y

且(X+Y)G(X+Y)=X+Y，G(X+Y)G=G，即结论成立.

2　主要结论

设

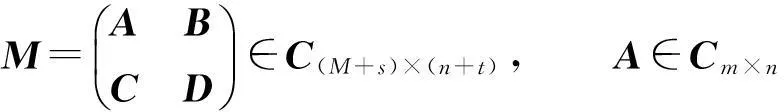
本部分主要来讨论分块矩阵M的{1,2}逆,{1,3}逆,{1,4}逆以及MP逆的显式表示问题.

记

EA=I-AA+,FA=I-A+A,Z=D-CA+B，U=EAB,V=CFA,S=EVZFU.

注意到：

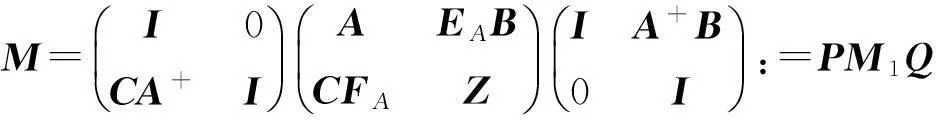
从而，

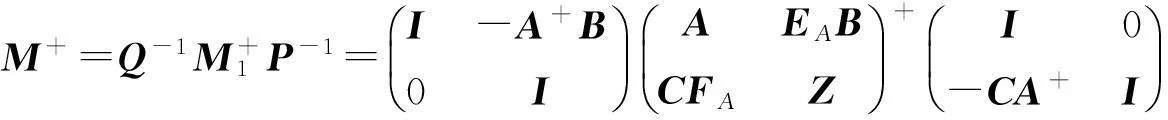
(1)

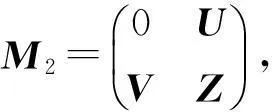
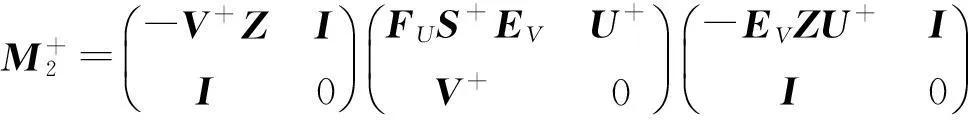
此时，

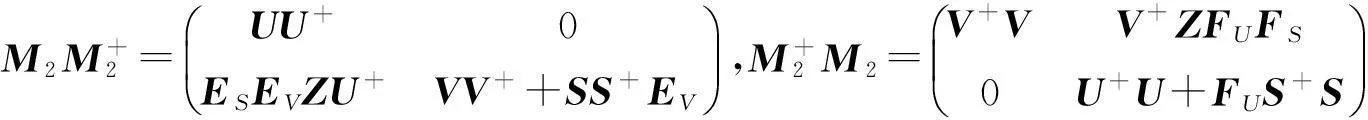
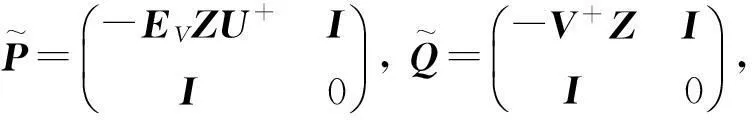
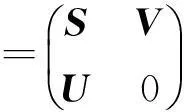
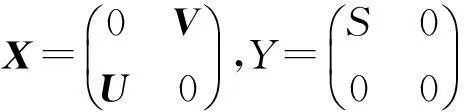
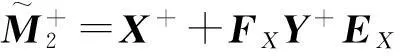
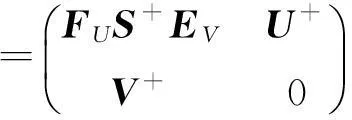
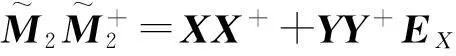
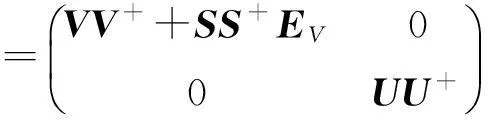
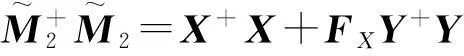
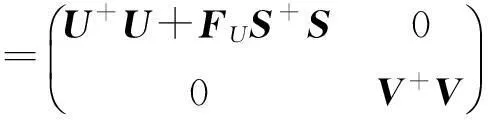
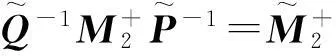
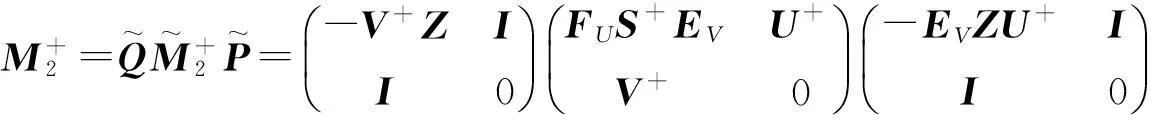
且

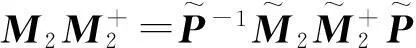
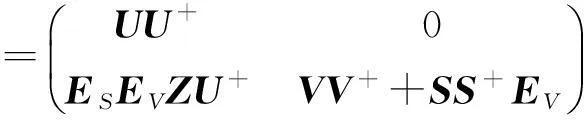
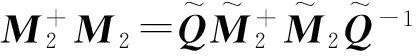
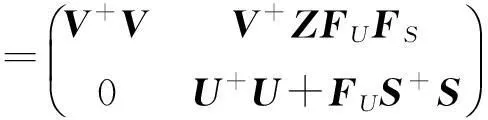
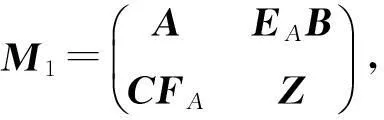
且

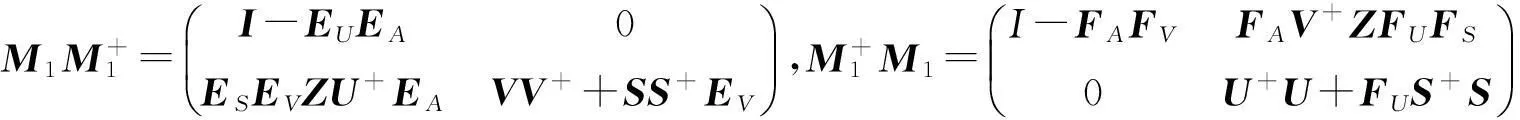
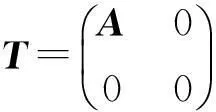
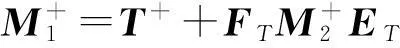
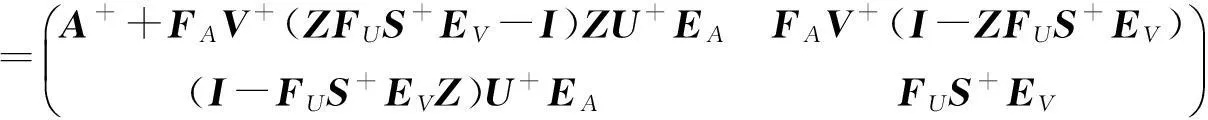
再由引理9 及引理10得

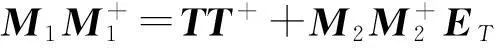
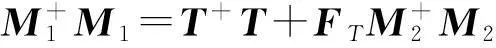
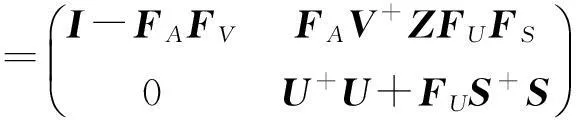
利用公式(1),得出2×2分块矩阵M的{1,2}逆的显式表达式:

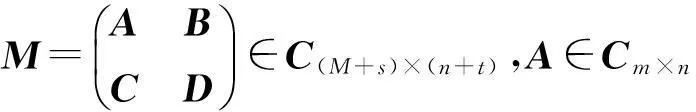
其中

A+BFUS+EVCA+；

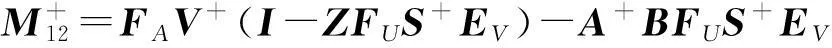
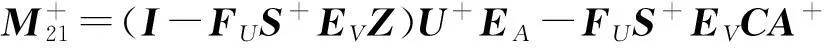
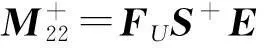
此时，

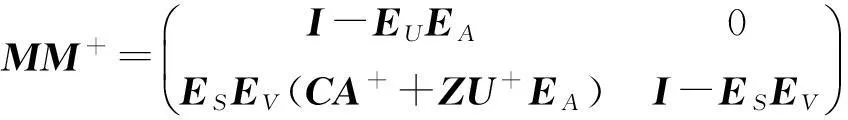
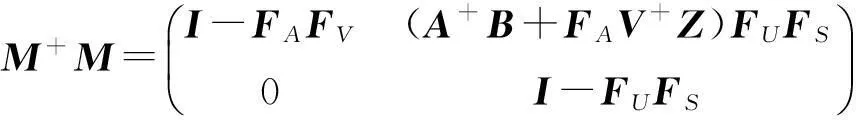
证明：由公式(1)及引理11得

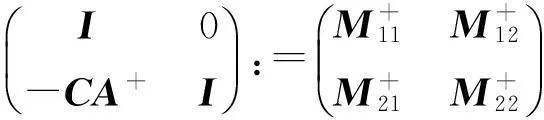
其中：

A+BFUS+EVCA+；

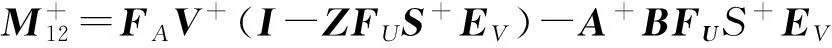
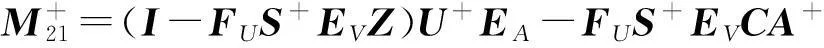
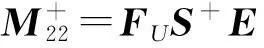
且有

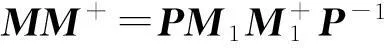
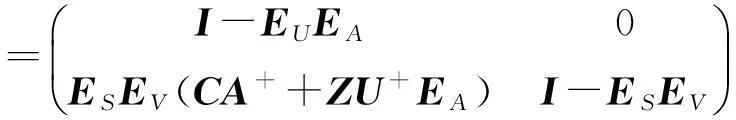
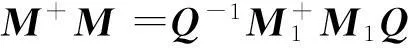
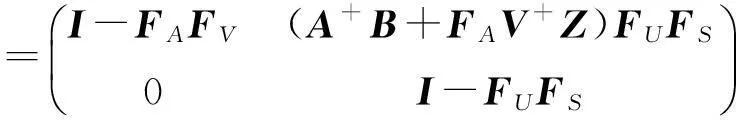
注意到,在定理1中M+的表示与子块的{1,2}逆的选择有关. 接下来，考虑分块矩阵M的{1,3}逆,{1,4}逆以及MP逆的表示问题. 为计算方便，在下文中选取子块的MP逆,重新记：

EA=I-AA+,FA=I-A+A,Z=D-CA†B，U=EAB,V=CFA,S=EVZFU.

于是有下列各式成立：

U†EA=U†, U†A=0,A†U=0, US†=0,S†EV=S†, V†S=0,

FAV†=V†, AV†=0,VA†=0,S†V=0,FUS†=S†, SU†=0,

以及

EUEA=I-AA†,-UU†, ESEV=I-VV†-SS†,

FAFV=I-A†A-V†V,FUFS=I-U†U-S†S,

(2AA†+2UU†-I)-1=2AA†+2UU†-I, (2VV†+2SS†-I)-1=2VV†+2SS†-I,

(2A†A+2V†V-I)-1=2A†A+2V†V-I,(2U†U+2S†S-I)-1=2U†U+2S†S-I,

(2VV†+2SS†-I)ESEV=-ESEV,FUFS(2U†U+2S†S-I)=-FUFS.

结合定理1可知此时

(2)

其中：

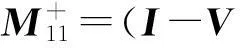
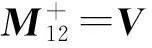
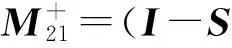
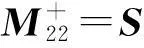
且有

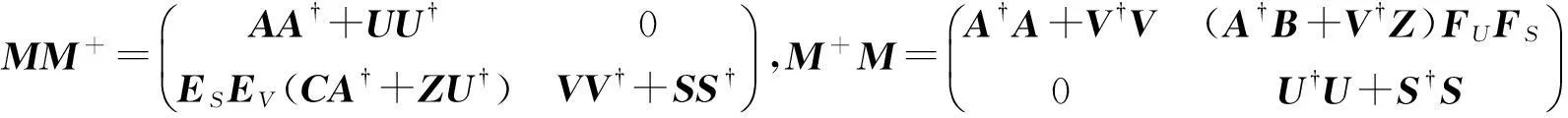
记

Δ1=(2VV†+2SS†-I)-ESEV(CA†+ZU†)(2AA†+2UU†-I)-1[ESEV(CA†+ZU†)]*

=(2VV†+2SS†-I){I+ESEV(CA†+ZU†)[ESEV(CA†+ZU†)]*}，

ξ1=I+ESEV(CA†+ZU†)[ESEV(CA†+ZU†)]*，

则

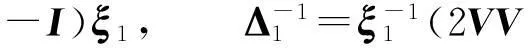
记

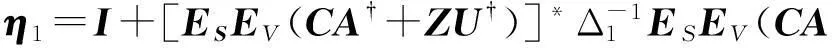
则由引理2可得：

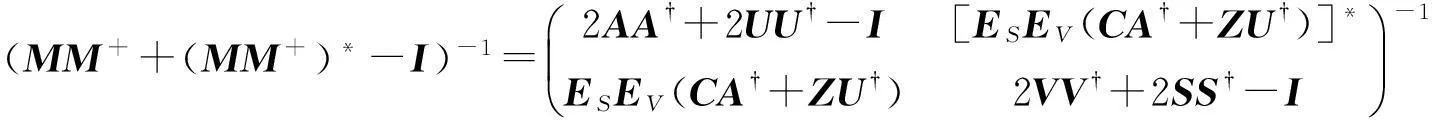
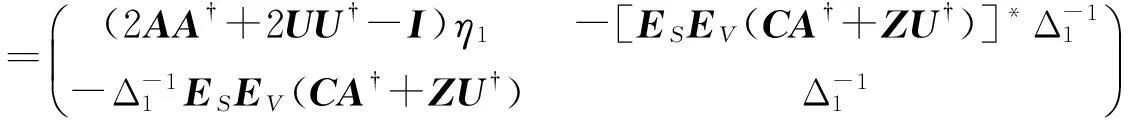
(3)

类似地, 记

ξ2=I+[(A†B+V†Z)FUFS]*(A†B+V†Z)FUFS,

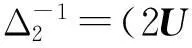
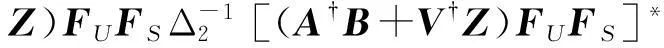
则

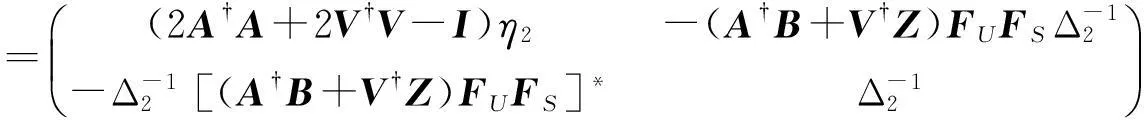
(4)

结合引理5,引理6, 得到如下结论：

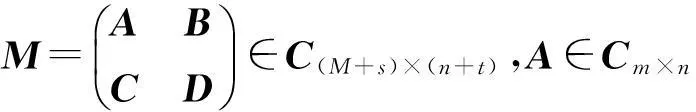
(1)M有一个{1,3}逆为

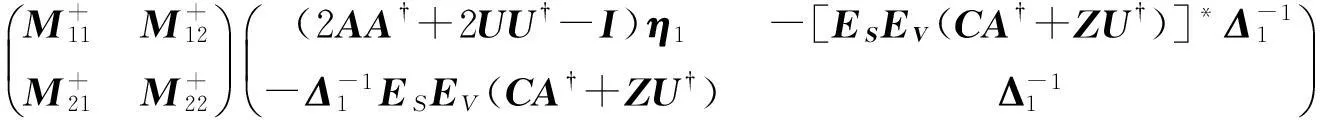
(2)M有一个{1,4}逆为

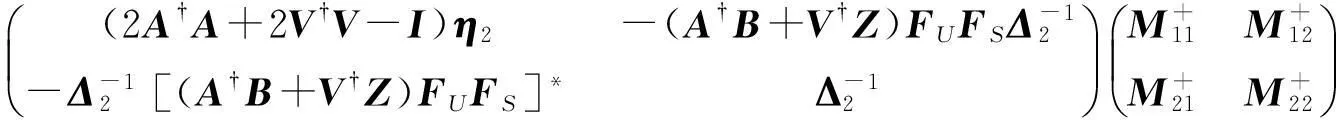
其中

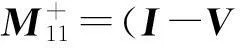
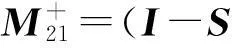
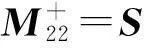
证明：(1)由引理5及公式2,公式3可得; (2)由引理6及 公式2, 公式4可得.

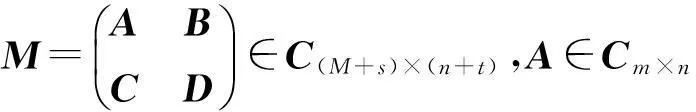
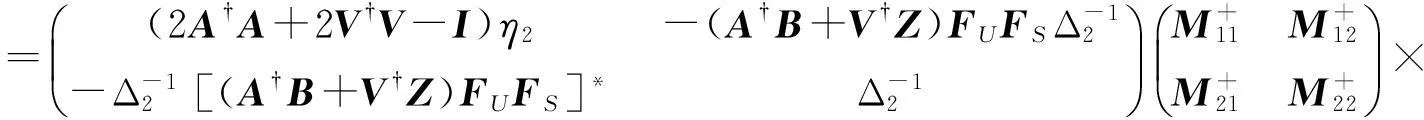
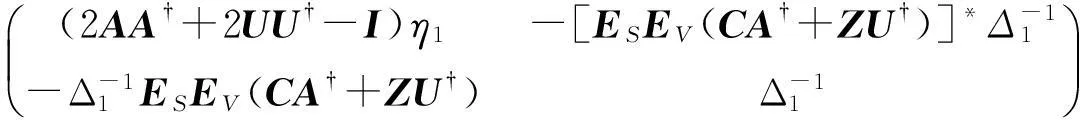
其中

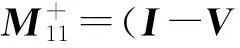
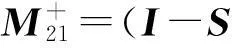
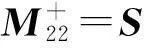
证明： 由引理1及公式(2),公式(3),公式(4)可得.

参考文献：

[1] Moore E H.On thereciprocal of the general algebra matrix (Abstract)[J].Bull Amer Math Soc,1920,26:394|395.

[2] Penrose R.A generalized inverse for matrices[J].Cambridge University Press,1955,51(3):406|413.

[3] Ben|Israel A,Greville T N E.Generalized inverses: theory and applications[M].Springer Science & Business Media,2003.

[4] Xue Y.Stable perturbations of operators and related topics[M].Singapore:World Scientific,2012.

[5] Du F,Xue Y.The reverse order law for Moore|Penrose inverse of closed operators[J].数学季刊.2013,28(1):139|146

[6] Chen G,Xue Y.The expression of the generalized inverse of the perturbed operator under Type I perturbation in Hilbert spaces[J].Linear algebra and its applications,1998,285(1):1|6.

[7] Hartwig R E.Block generalized inverses[J].Archive for Rational Mechanics and Analysis,1976,61(3):197|251.

[8] 陈永林.广义逆矩阵的理论与方法[M].南京：南京师范大学出版社，2005.

[9] Horn R A,Johnson C R.Matrix analysis[M].Cambridge University Press,2012.

[10] Du F，Xue Y,The expression of the Moore|Penrose inverse of A|XY*[J].华东师范大学学报：自然科学版,2010(5):33|37.

The Expression for the Generalized Inverse of Block Matrix

DU Fapeng1,2

(1.Department of Mathematics, Southeast University, Nanjing 210096, China;

2.Collage of mathematics & Physical Sciences, Xuzhou Institute of Technology, Xuzhou 221008, China)

Abstract:By decomposition,this paper presented the explicit expressions for the {1,2} inverse, {1,3} inverse and {1,4} inverse of block matrix,respectively.Using the expression of {1,2} inverse,the expression for the Moore|Penrose inverse of was got.

Key words:blocking matrix; generalized inverse; Moore|Penrose inverse

(编辑崔思荣)