考虑负载均衡的过驱动航天器推力器分配方法

张世杰，段晨阳，赵亚飞

(哈尔滨工业大学卫星技术研究所，哈尔滨150080)

0 引言

高性能航天器常采用冗余配置的推力器以提高系统在轨可靠性，构成一类过驱动系统。过驱动航天器的推力器分配方案并不唯一，增加了在轨推力分配的复杂性，却可为控制系统提供新的设计自由度，进而能够改善航天器控制系统性能。已有诸多学者针对推力分配问题提出了多种方法，包括固定

分配列表法［1，2］和动态分配法等［3－5］。固定分配列表法是根据推力器布局，预先制定推力分配列表，在运行过程中始终采用该方案，其主要缺点是需要预先制定推力器分配列表，包括推力器故障时的分配列表，这就需要占用巨大的星上存储空间，特别是静态推力器列表无法考虑执行机构特性，无法对该特性实时地调整分配策略应对不可预见的跟踪误差。

控制分配(Control allocation，CA)方法是由控制算法给出的期望控制量出发，在各类约束条件和最优目标下，将期望控制量在冗余配置的执行机构间进行分配，使执行机构的实际控制输出尽可能与期望控制量相吻合的一种控制设计技术［6］。Ricardo等［7］尝试将控制分配方法引入航天器推力控制问题，随后多位学者面向不同的控制性能，提出了诸多航天器推力分配算法［8－10］。

航天器在轨运行时，控制目标一般具有方向性，在推力器分配时如果不做限制，会出现仅有少数几个推力器承担主要控制任务的情况，导致这几个推力器的工作总时长或开关次数显著增加，相比于其它推力器会提前达到最大连续工作时长和继电器开关次数寿命，发生故障或失效。因此，在推力分配过程中，确保误差最小前提下，需要均衡分配给各推力器的负载，降低各推力器分配力矩之差，对提高推进系统整体工作寿命具有重要意义。如何利用推力器冗余配置特性，实现推力器负载均衡(Load balancing)分配，是一个亟待解决的问题。控制分配容许在一定的约束下，提出新的设计指标，并进行最优求解，为解决负载均衡问题提供了可行途径。

负载均衡的概念源自于计算机网络，用于处理多个节点间的协同工作问题，如用于P2P系统的负载平衡算法，其核心思想是将虚拟服务器分解，并且动态调节虚拟服务器的数量［11］。Wang等针对提高无线电网络系统利用率的问题，基于当前或过去临近节点的信息来满足整个数据流需求的思想，给出了每个节点的资源分配方案［12］。Frost等对飞机中的负载均衡控制分配问题进行了研究，基于一种min-max准则实现执行机构的均衡分配，并对该算法的敏感度进行了分析［13］。部分学者也探讨了航天领域的负载平衡方法［14－16］，但主要集中在编队飞行控制的燃料平衡问题。上述工作具有重要参考价值，但并不完善，难以直接应用。

本文以冗余配置推力器的小卫星作为研究对象，探索采用控制分配方法实现负载均衡控制目标的可行途径，期望本文的工作对高性能航天器控制系统设计能够提供一定的参考。

1 负载均衡分配问题描述

在航天器控制中，系统状态空间模型可以写成

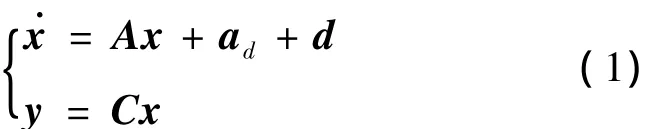
其中x∈Rm是系统状态量，d∈Rm为扰动项，ad∈Rm为通过控制器给出的控制指令，y∈Rk为观测向量。

在推力器进行航天器姿态/轨道控制过程中，满足

式中:F= ［F1，…，Fn］T，其各个元素分别代表各个推力器的推力大小，B为m×n阶矩阵。对于第i个推力器的大小，满足约束0≤Fi≤Fimax(i=1，…，n)。这里在给定的约束条件下，寻找“最优”解F的问题即为控制分配问题。

在给定约束条件下，控制分配问题可能存在多解、唯一解或无解三种情况。一种常见的，也是容易理解的方式，是降低控制分配误差以获取最佳的控制性能。除此以外，多推力器同时工作更容易实现姿态和轨道控制，尤其是在系统故障及恢复的过程中。因此，控制分配实际上包含两个层次的内容:一个是误差最小，另一个为控制优化。

控制分配的目的在于将控制器给出的期望控制指令，以一定的优化指标，分配给冗余的执行机构，从而优化配置，提高控制系统性能，原理如图1所示。

图1 控制分配原理图Fig.1 Schematic diagram of control allocation

考虑一般的控制分配模型

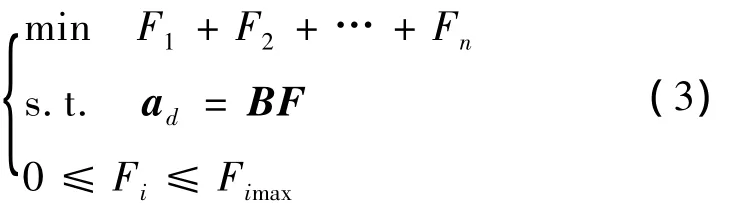
式中:B为由推力器安装布局确定的矩阵，称之为控制效率矩阵，控制效率矩阵的计算过程见文献［3］，Fimax分别为第i个推力器标称的最大推力。

在不考虑推力器上限约束的情况下，该控制分配模型可以通过简单的Lagrange算法求解［17］，当考虑推力器上限约束时，可通过零空间方法对饱和情况进行修正求解［18］。然而，力矩最优目标下的解不能保证均衡分配效果，且在给出初解之后予以被动修正，将饱和分配量赋予最大值，这种策略不能预先调节控制分配指令，无法达到在满足约束条件下实现力矩最优的分配效果。

2 控制分配的公式化表述

如前所述，控制分配包含两个层次的内容:误差最优和分配优化，下文将分别给出其数学描述。

误差最优:根据推力器安装构型矩阵B，寻求推力器分配向量F，满足，

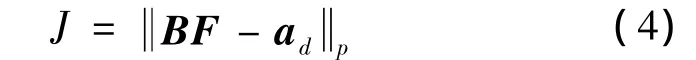
最小，并满足执行机构约束0≤Fi≤Fimax，其中向量范数为p范数。如果控制器给出的力和力矩指令在推力器可达集内，那么显然使得方程(4)得到最优解的条件为J=0，进而说明推力器的能力能够完成当前控制器的控制指令。但实际上，该条件并不一定成立，尤其是在某种特定情形下，如采用小推力发动机，大角度机动等，因此，考虑该分配目标极其必要。

分配优化:在给定推力器安装构型矩阵B，向量Fg满足0≤Fg≤Fmax时，寻找向量F满足

使得

混合优化:给定推力器安装构型矩阵B，进一步将优化指标修改为，寻找向量F满足

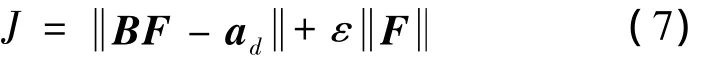
并满足

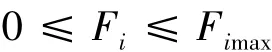
混合优化是将误差最优和分配最优两种不同的优化指标通过参变量ε变成一个统一的优化指标，如果选择较大的ε，则分配结果更趋向于分配最优;如果选择较小的ε，那么结果更趋向于误差最优。

选择不同的范数可以达到不同的控制目标，对于向量x∈Rm，向量范数分别定义为:

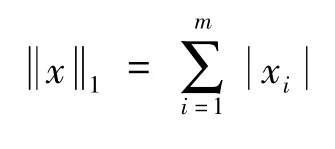
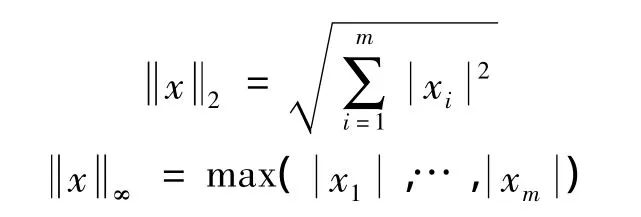
显然，对于误差最优，可以选择多种方案，都能够表示控制分配误差最小，可针对具体的求解复杂性确定;而对于控制最优指标，选择无穷范数是减小各推力器的最大值，从而降低分配给推力器的最大推力，增加利用率低的推力器的工作负荷，达到均衡分配的目的。这种均衡是一种相对“均衡”的概念，由控制指令确定，并非指最终分配给推力器的推力相等。通过设计一定目标函数，满足控制器指令的要求，同时考虑了推力器间负荷均衡的效果，合理的分配给各个执行机构，因此，该方法是一种全局的均衡推力器控制分配策略。

3 负载均衡分配算法

3. 1 控制分配算法

应用上节给出的混合优化控制分配模型，考虑负载均衡的控制分配模型可表示为其中，误差最优选择1范数，控制最优选择无穷范数，即负载均衡的概念。

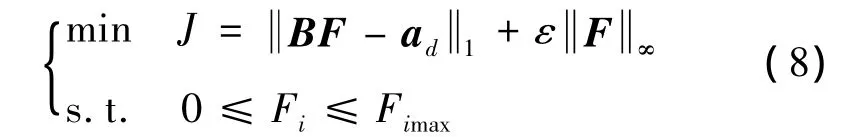
显然，上述控制分配模型无法直接求解，需要将其转化为标准的优化模型，并基于现有的优化算法进行求解。

引入参变量F*，满足F*= F∞，并引入一个新的标量函数y=s(x)，该函数定义为

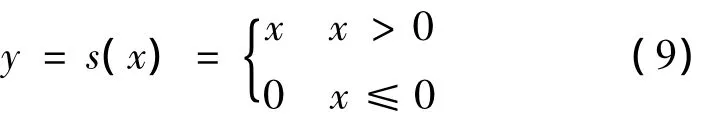
相应的向量函数y=s(x)定义为，对于x∈Rm

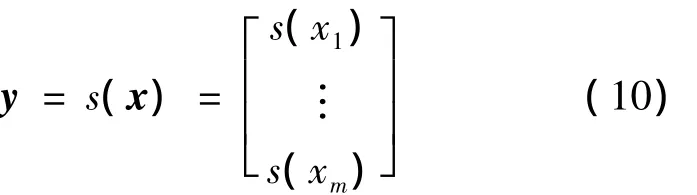
根据s函数的定义，引入如下松弛变量

以及误差松弛变量

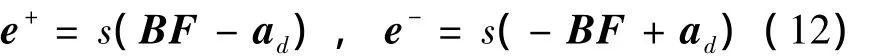
于是有

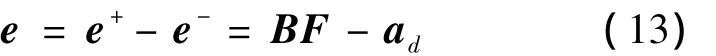
令各推力器最大值的集合为Fmax=［F1max，…，Fnmax］T，则有

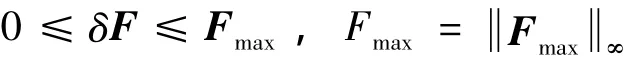
对于误差e，令emax=s(ad)+s(－ad)，则有，

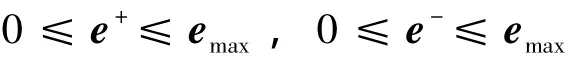
于是控制分配模型可以转化为标准的线性规划模型

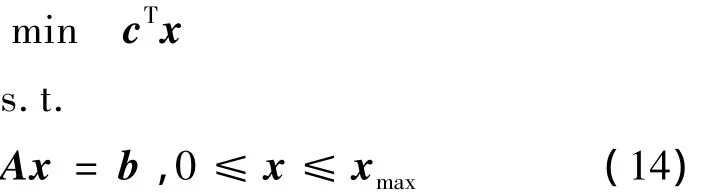
式中:

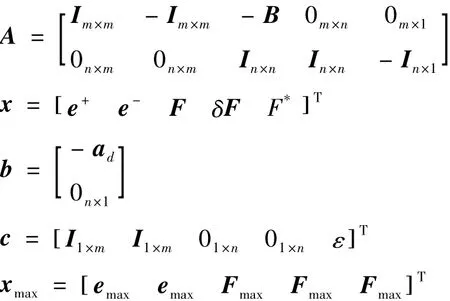
上述模型具有标准线性规划模型的形式，因此基于现有的线性分配算法可以进行求解［19－20］。

3. 2 算法评价指标

本文主要采用两种指标，用于评价执行机构负载均衡算法性能:平衡度和敏感度。

3.2.1 负载裕度与平衡度

定义第i个推力器的负载裕度

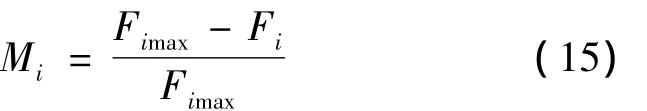
在给定配置下推力器的平均负载裕度为

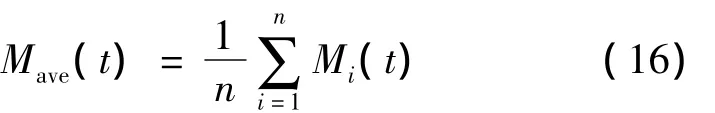
平衡度定义为推力器配置下的整体平均负载裕度，可定义为

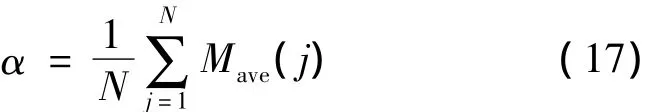
式中:N为采样时间点的数目。

显然，在推力器均未工作在最大推力时，平均负载裕度越大，说明推力器平均输出距离推力器阈值越远，越能够避免出现推力器工作在最大负荷的几率。

3.2.2 敏感度

对于控制器算法给出的期望力矩指令Tcmd，加以一小的常值偏差向量Δ，会导致执行机构指令发生变化，定义执行机构指令变化的程度为敏感度。其表达式为

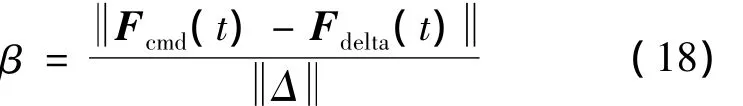
式中:Fcmd为未加偏差的执行机构指令，Fdelta为具有偏差时的执行机构指令。

由敏感度定义可知，敏感度越低时，执行机构的指令分配越理想，对误差的敏感程度越低。

综上，平衡度表征执行机构负载均衡状况，平衡度越高，则执行机构出现饱和状况的可能性越小;而敏感度表征算法对干扰的敏感程度，敏感度越低，则误差分配导致执行机构的出现饱和的可能性越小，表现为一定的鲁棒性。

4 仿真及结果分析

推力器姿态控制的控制效率矩阵为

以某型小卫星基于推力器的高精度姿态稳定控制问题为背景，小卫星的质量为10 kg，转动惯量为I= ［6.292 0 0;0 5.477 0;0 0 2.687］kg·m2;初始姿态四元数为 q(t0)= ［0.7035 －0.4708 0.3430 0.4073］T;初 始 姿 态 角 速 度 ωb0= ［0.9 0.6 0.7］Trad/s;控制器采用PD控制律，控制律参数kp=2.4 ，kd=3.9 。

为了能够对比说明均衡控制分配的效果，采用该算法和燃料最优推力器控制分配方法进行对比，燃料最优分配方法的模型可以写为

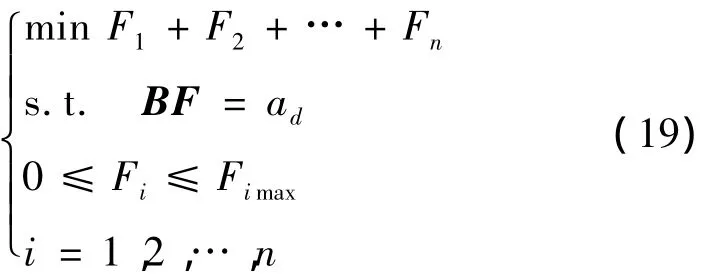
该模型是一个标准线性规划模型，求解该模型的线性分配算法可参考文献［21］。

在给定的安装构型及控制效率矩阵B下，记矩阵B的每i列编号为#i的推力器分别在三个坐标轴的分量，每个推力器的最小推力均为0.01 N，最大为10 N，推力器可以产生连续推力。在给定的推力器配置和控制律作用下，姿态角速度和姿态四元数的变化情况如图2和图3所示。可以看出姿态角速度逐渐趋于0，同时从姿态四元数的变化可以看出小卫星从初始姿态完成机动，进入稳态过程。

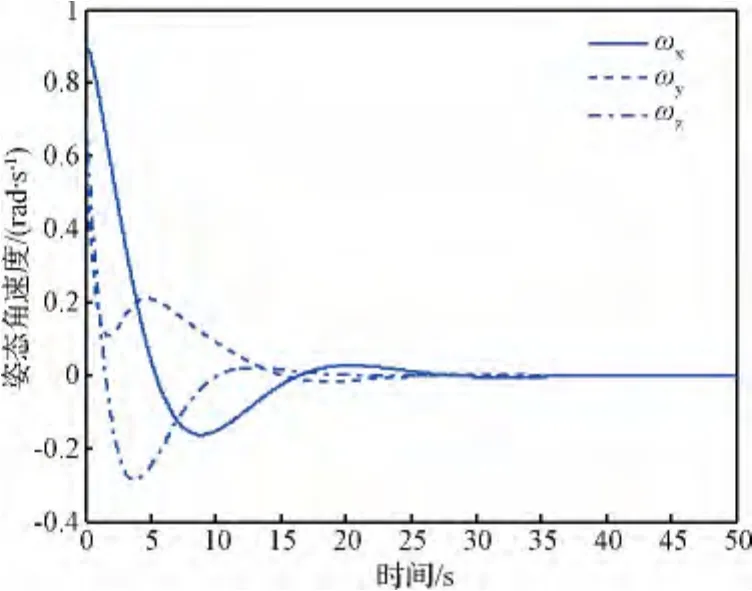
图2 姿态角速度随时间变化曲线Fig.2 Attitude angular velocity curve change with time

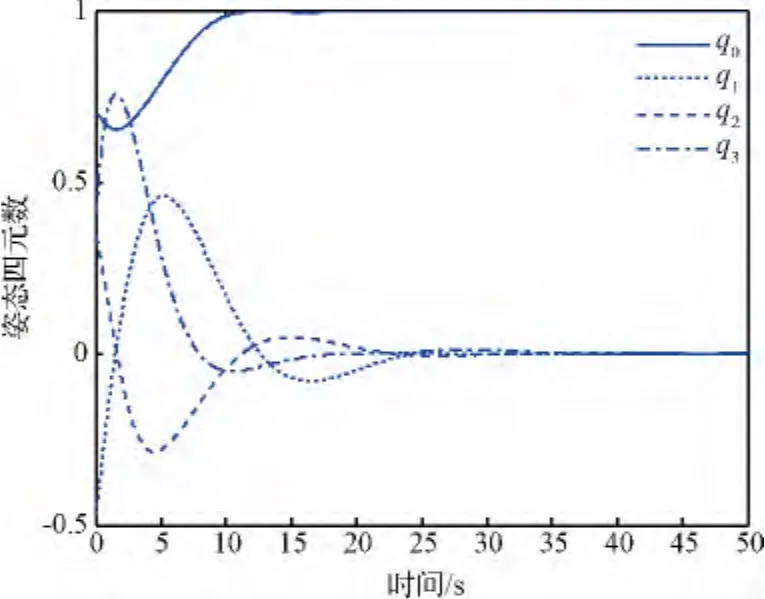
图3 姿态四元数随时间变化曲线Fig.3 Attitude quaternion curve change with time

在姿态控制过程，各个推力器的工作状态如图4所示。其中4a)和4b)是负载平衡下的推力器分配结果，而4c)和4d)是燃料最优控制分配时各个推力器的工作状态，灰色填充部分为推力器的工作时间段，非填充区域表示推力器处于关机状态，每个推力器柱状图后面的数字表示推力器工作期间输出的最大推力。

从图4中可以得出以下几点结论:

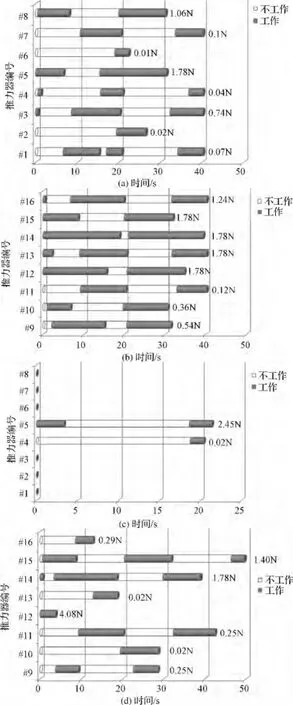
图4 负载均衡分配时的推力器工作情况(a和b)及燃料最优分配时的推力器工作情况(c和d)Fig.4 Working status of thrusters under balancing control allocation(a＆b)，and optimal fuel-consumption allocation(c＆d)

(1)推力器工作数目:在进行姿态控制期间，采用负载均衡控制分配方法时所有推力器都参与了工作，而燃料最优控制分配方法参与控制的推力器只有10个。这说明了负载均衡控制分配方法能够合理利用推力器的安装布局，使推力器间彼此协同工作，避免频繁使用部分推力器，从而均衡各推力器的利用率;

(2)系统进入稳态时间:采用负载均衡控制分配方法时，系统进入稳态的时间为40.2 s，而采用燃料最优控制分配方法时，系统进入稳态时间为49.6 s;可见，采用负载均衡控制分配方法能充分利用多推力器协同工作降低系统稳态时间，这对于工程实际应用是十分有意义的;

(3)最大推力:采用负载均衡控制分配方法时，最大推力输出为#5，#12，#13，#14，#15 推力器，均为1.78 N，采用燃料最优控制分配方法时，最大推力输出是#12推力器，大小为4.08 N;可见，负载均衡控制分配方法能够减小最大分配推力达56.4%，可见该方法能够有效降低某一或某些推力器工作负荷。

(4)推力器总工作时间:采用负载均衡控制分配方法时，所有16个推力器的工作时间总和为306.3 s，而燃料最优控制分配方法的推力器工作时间总和仅为111 s，这也说明负载均衡控制分配方法所达到的优化效果是以增加总的推力器工作时间为代价的;但是，在燃料最优控制分配方法中工作时间较长的推力器，如#11，#15推力器，在负载均衡控制分配方法中，工作时间均有所减少。

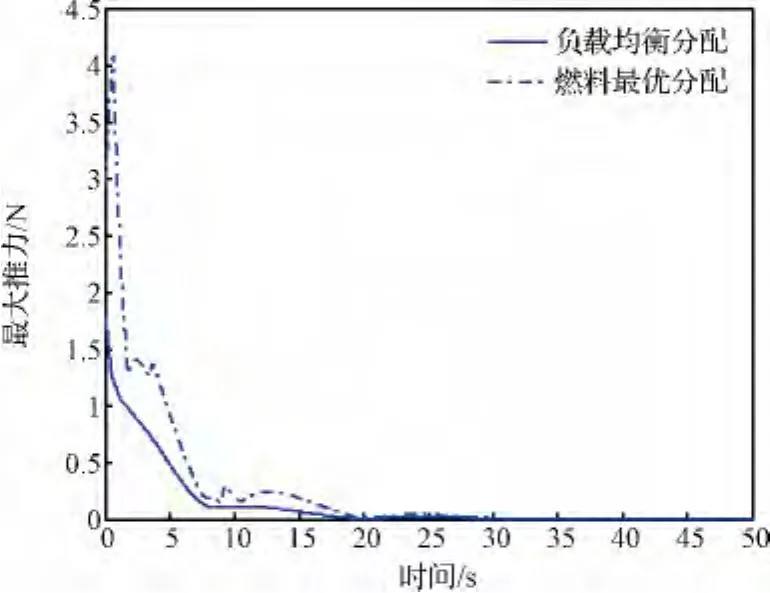
图5 最大推力变化曲线Fig.5 The curve of maximum thrusters change

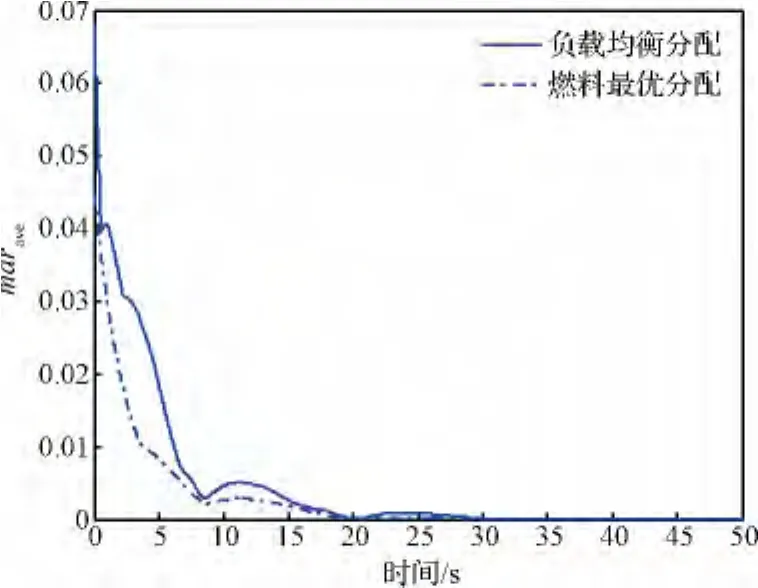
图6 平均负载裕度变化曲线Fig.6 The curve of average payload margin change

表1 两种算法评价对比结果Table 1 The comparison of two algorithms

(5)总燃料消耗:燃料消耗常用速度增量表示，采用燃料最优的控制分配方法时总速度增量为0.0024 km/s，而负载均衡的控制分配方法的速度增量为0.0032 km/s。可见，负载均衡的控制分配方法比燃料最优的控制分配增加燃料消耗约33.3%。

图5和图6分别给出了姿态控制过程中，各个时刻下分配给推力器的最大推力变化曲线和平均负载裕度变化曲线，燃料最优控制分配曲线始终位于负载均衡控制分配曲线上方，更直观的体现出了本文提出的控制分配方法能够有效的降低分配给推力器的最大控制指令分量，优化控制过程，使得推力器间分配更为均衡、合理。

通过表1可以看出，负载均衡控制分配方法能够增加推力器配置的平衡度，同时降低对扰动信号的敏感程度，从而提高控制系统性能。

5 结论

本文通过对负载均衡控制分配策略进行建模，并转化为线性规划模型，通过仿真，在给定的评价指标下进行了验证，得到了以下结论:

(1)负载均衡控制分配方法能够充分利用推力器冗余特性，通过增加推力器执行数目，达到减小推力器最大分配推力，减小控制系统进入稳态时间的目的;

(2)负载均衡控制分配方法能有效增加推力器配置的平衡度，将控制器指令“平均”分配给各个退器，同时在存在扰动力矩时，负载均衡控制分配方法对扰动误差不敏感，鲁棒性强。

［1］ Martel F.Optimal simultaneous 6 axis command of a space vehicle with a precomputed thruster selection catalogue table［J］.Advances in the Astronautical Sciences，2004，116:1 －13.

［2］ 王敏，解永春.考虑推力器推力上界及故障情况的航天器实时指令分配最优查表法［J］.宇航学报，2010，31(6):1540－1546.［Wang Min，Xie Yong-chun.Spacecraft thrusters real time command allocation algorithm in consideration of thrust upper bounds and thruster failure［J］.Journal of Astronautics，2010，31(6):1540 －1546.］

［3］ 唐生勇，张世杰，陈闽等.交会对接航天器推力器分配算法研究［J］.宇航学报，2008，29(4):1120－1125.［Tang Sheng-yong，Zhang Shi-jie，Chen Min，et al.Research on a thrust Allocation algorithm of spacecraft in RVD［J］.Journal of Astronautics，2008，29(4):1120 －1125.］

［4］ Ankersen F，Wu S F，Aleshin A，et al.Optimization of spacecraft thruster management function［J］. Journal of Guidance，Control，and Dynamics，2005，28(6):1283 －1290.

［5］ Pablo A S，Ricardo S P.Spacecraft thruster control allocation problems［J］.IEEE Transaction on Automatic Control，2005，50(2):245－249.

［6］ Wayne C D.Constrained control allocation［J］.Journal of Guidance，Control，and Dynamics，1993，16(4):717 －725.

［7］ Ricardo SP，Roberto A，Pablo A S.Robust optimal solution to the attitude/force control problem［J］.IEEE Transaction on Aerospace and Electronic Systems.2000，36(3):784 －792.

［8］ 陈玮，解永春.基于多目标规划的交会对接推力器指令分配方法［J］.航天控制，2007，25(3):33－38.［Chen Wei，Xie Yong-chun.A method of command distributing of thrusters in rendezvous and docking based on multi-objective programming［J］.Aerospace Control，2007，25(3):33 －38.］

［9］ Pablo A S.Control allocation for gimballed/fixed thrusters［J］.Acta Astronautica，2010，66(3－4):587－594.

［10］ Tang SY，Zhang SJ，Zhang Y L.A modified direct allocation algorithm with application to redundant actuators［J］.Chinese Journal of Aeronautics，2011，24(3):299 －308.

［11］ Yang L，Chen Z X.A VS-split load balancing algorithm in DHT-based P2P systems［C］.2012 International Conference on Systems and Informatics，Yantai，China，May 19 －20，2012.

［12］ Wang W，Kang G.S，Wang WB.Distributed resource allocation based on queue balancing in multihop cognitive radio networks［J］.IEEE/ACM Transactions on Networking，2012，20(3):837－850.

［13］ Susan A F，Marc B.Resource balancing control allocation［C］.2010 American Control Conference，Baltimore，USA，June 30－July 2，2010.

［14］ Beard R W，McLain T W，Hadaegh F Y.Fuel optimization for constrained rotation of spacecraft formations［J］.Journal of Guidance，Control，and Dynamics，2000，23(2):339 －346.

［15］ Rahmani A，Mesbahi M，Hadaegh F Y.Optimal balancedenergy formation flying maneuvers［J］.Journal of Guidance，Control，and Dynamics，2006，29(6):1395 －1403.

［16］ Bodson M，Frost SA.Load balancing in control allocation［J］.Journal of Guidance，Control，and Dynamics，2011，34(2):380－387.

［17］ Kenneth A B，Wayne C D.Null-space augments solutions to constrained control allocation problems［C］.Baltimore:AIAA Guidance，Navigation and Control Conference，1995:328 －333.

［18］ 张世杰，赵亚飞，陈闽等.过驱动轮控卫星的动态控制分配方法研究［J］.航空学报，2011，32(7):1260－1268.［Zhang Shi-jie，Zhao Ya-fei，Chen Min，et al.Dynamic control allocation for overactuated satellite with redundant reaction wheels［J］.Acta Aeronautica et Astronautica Sinica，2011，32(7):1260 －1268.］

［19］ Johansen T A，Fossen T I.Control allocation—a survey［J］.Automatica，2013，49(5):1087－1103.

［20］ Marc B.Evaluation of optimization methods for control allocation［J］.Journal of Guidance，Control，and Dynamics.2002，25(4):703－711.

［21］ Jin J，Park B，Park Y，et al.Attitude control of a satellite with redundant thrusters［J］.Aerospace Science and Technology，2006，10(7):644－651.